6edo
| ← 5edo | 6edo | 7edo → |
(convergent)
6 equal divisions of the octave (abbreviated 6edo or 6ed2), also called 6-tone equal temperament (6tet) or 6 equal temperament (6et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 6 equal parts of exactly 200 ¢ each. Each step represents a frequency ratio of 21/6, or the 6th root of 2. It is also known as the whole tone scale.
Theory
6edo is identical to the 12edo whole-tone scale, however, it does have xenharmonic theoretical appeal. The 6-form is a simple basis for harmony in the 2.5.7 subgroup, somewhat like the 7-form for 2.3.5 and the 5-form for 2.3.7. This means that 6edo itself can be seen as a particularly crude tuning of temperaments like didacus, in the same way as 7edo for meantone or 5edo for superpyth. The root chord in this harmonic system can be seen as:
- [0 2 5] = 4:5:7, with the harmonic seventh as a bounding interval
- [0 3 4] = 5:7:8, with the minor sixth as a bounding interval
- [0 1 3] = 7:8:10, with the large septimal tritone as a bounding interval
Whichever way, this is very different from standard functional harmony.
If the prime 3 is added, it leads to absurd interpretations such as father, as it is almost 100 cents sharp. However, in a composite subgroup, the 9th harmonic can be introduced, being directly approximated by 1 step of 6edo. In 2.9.5.7, the most salient fact about 6edo is that both 64/63 and 81/80 are tempered out, implying the restriction of both 2.3.7 superpyth and 2.3.5 meantone temperament (that is, dominant temperament) to 2.9.5.7.
6edo is the first edo to have lower consistency than the one that precedes it, and the highest edo that has no single period mode of symmetry scales other than using the single step as a generator. This means it is relatively poor for its size at creating traditional tonal music, with 5edo and 7edo both having much better representations of the third harmonic, but has still seen more use than most edos other than 12, since it can be played on any 12-tone instrument.
Notation
As a subset of 12edo, 6edo can be notated on a five-line staff with standard notation.
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +98.0 | +13.7 | +31.2 | -3.9 | +48.7 | -40.5 | -88.3 | +95.0 | -97.5 | -70.8 | -28.3 |
| Relative (%) | +49.0 | +6.8 | +15.6 | -2.0 | +24.3 | -20.3 | -44.1 | +47.5 | -48.8 | -35.4 | -14.1 | |
| Steps (reduced) |
10 (4) |
14 (2) |
17 (5) |
19 (1) |
21 (3) |
22 (4) |
23 (5) |
25 (1) |
25 (1) |
26 (2) |
27 (3) | |
Subsets and supersets
Intervals
| Degree | Cents | Interval region | Approximated JI intervals[note 1] | Audio | |||
|---|---|---|---|---|---|---|---|
| 3-limit | 5-limit | 7-limit | Other | ||||
| 0 | 0 | Unison (prime) | 1/1 (just) | ||||
| 1 | 200 | Major second | 9/8 (−3.910) | 10/9 (+17.596) | 28/25 (+3.802) 8/7 (−31.174) |
19/17 (+7.442) 55/49 (+0.020) 64/57 (−0.532) 17/15 (−16.687) |
|
| 2 | 400 | Major third | 81/64 (−7.820) | 5/4 (+13.686) | 63/50 (−0.108) 9/7 (−35.084) |
34/27 (+0.910) | |
| 3 | 600 | Tritone | 7/5 (+17.488) 10/7 (−17.488) |
24/17 (+3.000) 99/70 (−0.088) 17/12 (−3.000) |
|||
| 4 | 800 | Minor sixth | 128/81 (+7.820) | 8/5 (−13.686) | 14/9 (+35.084) 100/63 (+0.108) |
27/17 (−0.910) | |
| 5 | 1000 | Minor seventh | 16/9 (+3.910) | 9/5 (−17.596) | 7/4 (+31.174) 25/14 (−3.802) |
30/17 (+16.687) 57/32 (+0.532) 98/55 (−0.020) 34/19 (−7.442) |
|
| 6 | 1200 | Octave | 2/1 (just) | ||||
Notation
| Degree | Cents | 12edo subset notation | |
|---|---|---|---|
| Diatonic interval names | Note names (on D) | ||
| 0 | 0 | Perfect unison (P1) | D |
| 1 | 200 | Major second (M2) Diminished third (d3) |
E Fb |
| 2 | 400 | Major third (M3) Diminished fourth (d4) |
F# Gb |
| 3 | 600 | Augmented fourth (A4) Diminished fifth (d5) |
G# Ab |
| 4 | 800 | Augmented fifth (A5) Minor sixth (m6) |
A# Bb |
| 5 | 1000 | Augmented sixth (A6) Minor seventh (m7) |
B# C |
| 6 | 1200 | Perfect octave (P8) | D |
In 6edo:
- ups and downs notation is identical to standard notation;
- mixed sagittal notation is identical to standard notation, but pure sagittal notation exchanges sharps (#) and flats (b) for sagittal sharp (
) and sagittal flat (
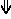) respectively.
Sagittal notation
This notation is a subset of the notations for EDOs 12, 18, 24, 36, 48, 60, 72, and 84.
Evo flavor
Because it includes no Sagittal symbols, this Evo Sagittal notation is also a conventional notation.
Revo flavor
Solfege
| Degree | Cents | 12edo subset standard solfege (movable do) |
12edo subset uniform solfege (2–3 vowels) |
|---|---|---|---|
| 0 | 0 | Do | Da |
| 1 | 200 | Re | Ra |
| 2 | 400 | Mi | Ma (M3) Fo (d4) |
| 3 | 600 | Fi (A4) Se (d5) |
Pa (A4) Sha (d5) |
| 4 | 800 | Si (A5) Le (m6) |
Su (A5) Fla (m6) |
| 5 | 1000 | Li (A6) Te (m7) |
Lu (A6) Tha (m7) |
| 6 | 1200 | Do | Da |
Regular temperament properties
Uniform maps
| Min. size | Max. size | Wart notation | Map |
|---|---|---|---|
| 5.6368 | 5.8101 | 6bcdeff | ⟨6 9 13 16 20 21] |
| 5.8101 | 5.8141 | 6bcde | ⟨6 9 13 16 20 22] |
| 5.8141 | 5.8774 | 6bde | ⟨6 9 14 16 20 22] |
| 5.8774 | 5.9258 | 6be | ⟨6 9 14 17 20 22] |
| 5.9258 | 5.9938 | 6b | ⟨6 9 14 17 21 22] |
| 5.9938 | 6.0804 | 6 | ⟨6 10 14 17 21 22] |
| 6.0804 | 6.2149 | 6f | ⟨6 10 14 17 21 23] |
Commas
6et tempers out the following commas. This assumes val ⟨6 10 14 17 21 22].
| Prime limit |
Ratio[note 2] | Monzo | Cents | Color name | Name(s) |
|---|---|---|---|---|---|
| 3 | 32/27 | [5 -3⟩ | 294.13 | Wa | Pythagorean minor third |
| 5 | 25/24 | [-3 -1 2⟩ | 70.67 | Yoyo | Dicot comma, classic chroma |
| 5 | 128/125 | [7 0 -3⟩ | 41.06 | Trigu | Augmented comma, diesis |
| 5 | 3125/3072 | [-10 -1 5⟩ | 29.61 | Laquinyo | Magic comma, small diesis |
| 5 | (12 digits) | [17 1 -8⟩ | 11.45 | Saquadbigu | Würschmidt comma |
| 5 | (30 digits) | [-44 -3 21⟩ | 6.72 | Trila-septriyo | Mutt comma |
| 7 | 49/48 | [-4 -1 0 2⟩ | 35.70 | Zozo | Semaphoresma, slendro diesis |
| 7 | 50/49 | [1 0 2 -2⟩ | 34.98 | Biruyo | Jubilisma, tritonic diesis |
| 7 | 3136/3125 | [6 0 -5 2⟩ | 6.08 | Zozoquingu | Hemimean comma |
| 7 | 6144/6125 | [11 1 -3 -2⟩ | 5.36 | Sarurutrigu | Porwell comma |
| 7 | 2401/2400 | [-5 -1 -2 4⟩ | 0.72 | Bizozogu | Breedsma |
| 11 | 121/120 | [-3 -1 -1 0 2⟩ | 14.37 | Lologu | Biyatisma |
| 11 | 176/175 | [4 0 -2 -1 1⟩ | 9.86 | Lorugugu | Valinorsma |
| 11 | 385/384 | [-7 -1 1 1 1⟩ | 4.50 | Lozoyo | Keenanisma |
| 13 | 13/12 | [-2 -1 0 0 0 1⟩ | 138.57 | tho 2nd | Tridecimal neutral second |
Music
- 6edo improvisation (2024)
- "Bowser breaks into Arnold Schoenberg's house and steals six of the twelve Tone Crystals (every other one), activating The 666666-Year-Curse Mechanism", from STAFFcirc vol. 7 (2021) – SoundCloud | Bandcamp
- Dvandva (1987/2007)
- From The Equal-Tempered Keyboard (1999–2022)
- "Prelude in 6ET" – Bandcamp | SoundCloud[dead link]
- "Invention in 6ET" – Bandcamp | SoundCloud[dead link]
- Heximal (2024)
Notes
- ↑ Based on treating 6edo as a subset of 12edo, itself treated as a 2.3.5.7.17.19 subgroup temperament; other approaches are also possible. For example, for 6edo as a 2.5.7.9 subgroup temperament, ignore the "Other" column).
- ↑ Ratios longer than 10 digits are presented by placeholders with informative hints.