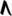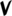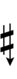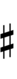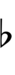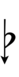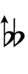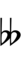50edo
| ← 49edo | 50edo | 51edo → |
50 equal divisions of the octave (abbreviated 50edo or 50ed2), also called 50-tone equal temperament (50tet) or 50 equal temperament (50et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 50 equal parts of exactly 24 ¢ each. Each step represents a frequency ratio of 21/50, or the 50th root of 2.
Theory
As an equal temperament, 50et tempers out 81/80 in the 5-limit, making it a meantone system, and in that capacity has historically drawn some notice; it is a somewhat sharp approximation of 2/7-comma meantone (and is almost exactly 5/18-comma meantone). In "Harmonics or the Philosophy of Musical Sounds" (1759) by Robert Smith, a musical temperament is described where the octave is divided into 50 equal parts – 50edo, in one word. Later, W. S. B. Woolhouse noted it was fairly close to the least squares tuning for 5-limit meantone. 50edo, however, is especially interesting from a higher-limit point of view. While 31edo extends meantone with a 7/4 which is nearly pure, 50 has a flat 7/4 but both 11/8 and 13/8 are nearly pure. It is also the highest edo where the mapping of 9/8 and 10/9 to the same interval is consistent, with two stacked fifths falling almost exactly 3/7-syntonic-comma sharp of 10/9 and 4/7-comma flat of 9/8. It also maps all 15-odd-limit intervals consistently, with the sole exceptions of 11/9 and 18/11.
It tempers out 126/125, 225/224 and 3136/3125 in the 7-limit, indicating it supports septimal meantone; 245/242, 385/384 and 540/539 in the 11-limit and 105/104, 144/143 and 196/195 in the 13-limit, and can be used for even higher limits. Aside from meantone and its extension meanpop, it can be used to advantage for the coblack temperament (15 & 50), and provides the optimal patent val for 11- and 13-limit bimeantone. It is also the unique equal temperament tempering out both 81/80 and the vishnuzma, [23 6 -14⟩, so that in 50edo seven chromatic semitones stack to a perfect fourth. By comparison, this gives a perfect fifth in 12edo, a doubly diminished fifth in 31edo, and a diminished fourth in 19edo.
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -6.0 | -2.3 | -8.8 | -11.9 | +0.7 | -0.5 | -8.3 | -9.0 | -9.5 | +9.2 | -4.3 | -4.6 | +6.1 | +2.4 | +7.0 |
| Relative (%) | -24.8 | -9.6 | -36.8 | -49.6 | +2.8 | -2.2 | -34.5 | -37.3 | -39.6 | +38.4 | -17.8 | -19.3 | +25.6 | +10.1 | +29.0 | |
| Steps (reduced) |
79 (29) |
116 (16) |
140 (40) |
158 (8) |
173 (23) |
185 (35) |
195 (45) |
204 (4) |
212 (12) |
220 (20) |
226 (26) |
232 (32) |
238 (38) |
243 (43) |
248 (48) | |
Relations
The 50edo system is related to 7edo, 12edo, 19edo, 31edo as the next approximation to the "Golden Tone System" (Das Goldene Tonsystem) of Thorvald Kornerup (and similarly as the next step from 31edo in Joseph Yasser's "A Theory of Evolving Tonality").
Intervals
| # | Cents | Ratios[note 1] | Ups and downs notation
(EUs: v3A1 and vvd2) | ||
|---|---|---|---|---|---|
| 0 | 0 | 1/1 | Perfect 1sn | P1 | D |
| 1 | 24 | 45/44, 49/48, 56/55, 65/64, 66/65, 78/77, 91/90, 99/98, 100/99, 121/120, 169/168 | Up 1sn | ^1 | ^D |
| 2 | 48 | 27/26, 33/32, 36/35, 50/49, 55/54, 64/63 | Dim 2nd, Downaug 1sn | d2, vA1 | Ebb, vD# |
| 3 | 72 | 21/20, 25/24, 26/25, 28/27 | Aug 1sn, Updim 2nd | A1, ^d2 | D#, ^Ebb |
| 4 | 96 | 22/21 | Downminor 2nd | vm2 | vEb |
| 5 | 120 | 16/15, 15/14, 14/13 | Minor 2nd | m2 | Eb |
| 6 | 144 | 13/12, 12/11 | Upminor 2nd | ^m2 | ^Eb |
| 7 | 168 | 11/10 | Downmajor 2nd | vM2 | vE |
| 8 | 192 | 9/8, 10/9 | Major 2nd | M2 | E |
| 9 | 216 | 25/22 | Upmajor 2nd | ^M2 | ^E |
| 10 | 240 | 8/7, 15/13 | Downaug 2nd, Dim 3rd | vA2, d3 | vE#, Fb |
| 11 | 264 | 7/6 | Updim 3rd, Aug 2nd | ^d3, A2 | ^Fb, E# |
| 12 | 288 | 13/11 | Downminor 3rd | vm3 | vF |
| 13 | 312 | 6/5 | Minor 3rd | m3 | F |
| 14 | 336 | 27/22, 39/32, 40/33, 49/40 | Upminor 3rd | ^m3 | ^F |
| 15 | 360 | 16/13, 11/9 | Downmajor 3rd | vM3 | vF# |
| 16 | 384 | 5/4 | Major 3rd | M3 | F# |
| 17 | 408 | 14/11 | Upmajor 3rd | ^M3 | ^F# |
| 18 | 432 | 9/7 | Downaug 3rd, Dim 4th | vA3, d4 | vFx, Gb |
| 19 | 456 | 13/10 | Updim 4th, Aug 3rd | A3, ^d4 | ^Gb, Fx |
| 20 | 480 | 33/25, 55/42, 64/49 | Down 4th | v4 | vG |
| 21 | 504 | 4/3 | Perfect 4th | P4 | G |
| 22 | 528 | 15/11 | Up 4th | ^4 | ^G |
| 23 | 552 | 11/8, 18/13 | Downaug 4th | vA4 | vG# |
| 24 | 576 | 7/5 | Aug 4th | A4 | G# |
| 25 | 600 | 63/44, 88/63, 78/55, 55/39 | Upaug 4th, Downdim 5th | ^A4, vd5 | ^G#, vAb |
| 26 | 624 | 10/7 | Dim 5th | d5 | Ab |
| 27 | 648 | 16/11, 13/9 | Updim 5th | ^d5 | ^Ab |
| 28 | 672 | 22/15 | Down 5th | v5 | vA |
| 29 | 696 | 3/2 | Perfect 5th | P5 | A |
| 30 | 720 | 50/33, 84/55, 49/32 | Up 5th | ^5 | ^A |
| 31 | 744 | 20/13 | Downaug 5th, Dim 6th | vA5, d6 | vA#, Bbb |
| 32 | 768 | 14/9 | Updim 6th, Aug 5th | ^d6, A5 | ^Bbb, A# |
| 33 | 792 | 11/7 | Downminor 6th | vm6 | vBb |
| 34 | 816 | 8/5 | Minor 6th | m6 | Bb |
| 35 | 840 | 13/8, 18/11 | Upminor 6th | ^m6 | ^Bb |
| 36 | 864 | 44/27, 64/39, 33/20, 80/49 | Downmajor 6th | vM6 | vB |
| 37 | 888 | 5/3 | Major 6th | M6 | B |
| 38 | 912 | 22/13 | Upmajor 6th | ^M6 | ^B |
| 39 | 936 | 12/7 | Downaug 6th, Dim 7th | vA6, d7 | vB#, Cb |
| 40 | 960 | 7/4 | Updim 7th, Aug 6th | ^d7, A6 | ^Cb, B# |
| 41 | 984 | 44/25 | Downminor 7th | vm7 | vC |
| 42 | 1008 | 16/9, 9/5 | Minor 7th | m7 | C |
| 43 | 1032 | 20/11 | Upminor 7th | ^m7 | ^C |
| 44 | 1056 | 24/13, 11/6 | Downmajor 7th | vM7 | vC# |
| 45 | 1080 | 15/8, 28/15, 13/7 | Major 7th | M7 | C# |
| 46 | 1104 | 21/11 | Upmajor 7th | ^M7 | ^C# |
| 47 | 1128 | 40/21, 48/25, 25/13, 27/14 | Downaug 7th, Dim 8ve | vA7, d8 | vCx, Db |
| 48 | 1152 | 52/27, 64/33, 35/18, 49/25, 108/55, 63/32 | Updim 8ve, Aug 7th | ^d8, A7 | ^Db, Cx |
| 49 | 1176 | 88/45, 96/49, 55/28, 128/65, 65/33, 77/39, 180/91, 196/99, 99/50, 240/121, 336/169 | Down 8ve | v8 | vD |
| 50 | 1200 | 2/1 | Perfect 8ve | P8 | D |
Notation
Ups and downs notation
Spoken as up, downsharp, sharp, upsharp, etc. Note that downsharp can be respelled as dup (double-up), and upflat as dud.
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
||||||
| Flat symbol | |
|
Using Helmholtz–Ellis accidentals, 50edo can also be notated using alternative ups and downs:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
| |
| Flat symbol | |
|
|
|
|
Here, a sharp raises by three steps, and a flat lowers by three steps, so arrows can be used to fill in the gap. If the arrows are taken to have their own layer of enharmonic spellings, some notes may be best spelled with double arrows.
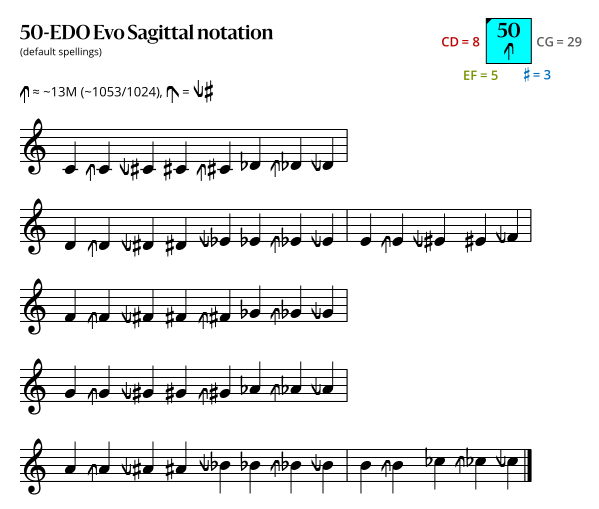
Sagittal notation
This notation uses the same sagittal sequence as EDOs 57, 64, and 71b.
Evo flavor
Revo flavor
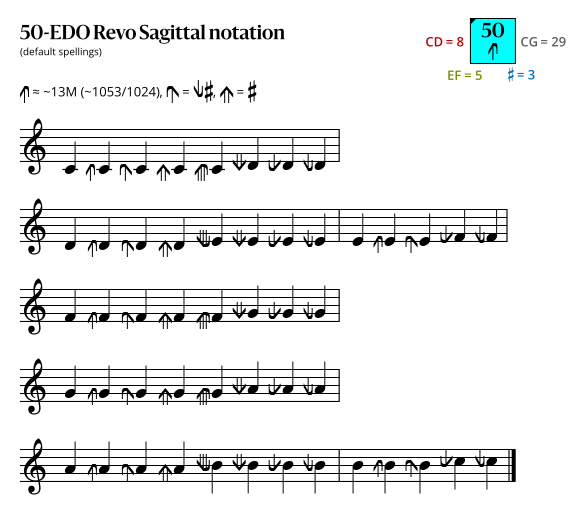
In the diagrams above, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's primary comma (the comma it exactly represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it approximately represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this EDO.
Approximation to JI

15-odd-limit interval mappings
The following tables show how 15-odd-limit intervals are represented in 50edo. Prime harmonics are in bold; inconsistent intervals are in italics.
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 13/8, 16/13 | 0.528 | 2.2 |
| 15/14, 28/15 | 0.557 | 2.3 |
| 11/8, 16/11 | 0.682 | 2.8 |
| 13/11, 22/13 | 1.210 | 5.0 |
| 13/10, 20/13 | 1.786 | 7.4 |
| 5/4, 8/5 | 2.314 | 9.6 |
| 7/6, 12/7 | 2.871 | 12.0 |
| 11/10, 20/11 | 2.996 | 12.5 |
| 9/7, 14/9 | 3.084 | 12.9 |
| 5/3, 6/5 | 3.641 | 15.2 |
| 13/12, 24/13 | 5.427 | 22.6 |
| 3/2, 4/3 | 5.955 | 24.8 |
| 7/5, 10/7 | 6.512 | 27.1 |
| 11/6, 12/11 | 6.637 | 27.7 |
| 15/13, 26/15 | 7.741 | 32.3 |
| 15/8, 16/15 | 8.269 | 34.5 |
| 13/7, 14/13 | 8.298 | 34.6 |
| 7/4, 8/7 | 8.826 | 36.8 |
| 15/11, 22/15 | 8.951 | 37.3 |
| 11/7, 14/11 | 9.508 | 39.6 |
| 9/5, 10/9 | 9.596 | 40.0 |
| 13/9, 18/13 | 11.382 | 47.4 |
| 11/9, 18/11 | 11.408 | 47.5 |
| 9/8, 16/9 | 11.910 | 49.6 |
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 13/8, 16/13 | 0.528 | 2.2 |
| 15/14, 28/15 | 0.557 | 2.3 |
| 11/8, 16/11 | 0.682 | 2.8 |
| 13/11, 22/13 | 1.210 | 5.0 |
| 13/10, 20/13 | 1.786 | 7.4 |
| 5/4, 8/5 | 2.314 | 9.6 |
| 7/6, 12/7 | 2.871 | 12.0 |
| 11/10, 20/11 | 2.996 | 12.5 |
| 9/7, 14/9 | 3.084 | 12.9 |
| 5/3, 6/5 | 3.641 | 15.2 |
| 13/12, 24/13 | 5.427 | 22.6 |
| 3/2, 4/3 | 5.955 | 24.8 |
| 7/5, 10/7 | 6.512 | 27.1 |
| 11/6, 12/11 | 6.637 | 27.7 |
| 15/13, 26/15 | 7.741 | 32.3 |
| 15/8, 16/15 | 8.269 | 34.5 |
| 13/7, 14/13 | 8.298 | 34.6 |
| 7/4, 8/7 | 8.826 | 36.8 |
| 15/11, 22/15 | 8.951 | 37.3 |
| 11/7, 14/11 | 9.508 | 39.6 |
| 9/5, 10/9 | 9.596 | 40.0 |
| 13/9, 18/13 | 11.382 | 47.4 |
| 9/8, 16/9 | 11.910 | 49.6 |
| 11/9, 18/11 | 12.592 | 52.5 |
Regular temperament properties
Temperament measures
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3 | [-79 50⟩ | [⟨50 79]] | +1.88 | 1.88 | 7.83 |
| 2.3.5 | 81/80, [-27 -2 13⟩ | [⟨50 79 116]] | +1.58 | 1.59 | 6.62 |
| 2.3.5.7 | 81/80, 126/125, 84035/82944 | [⟨50 79 116 140]] | +1.98 | 1.54 | 6.39 |
| 2.3.5.7.11 | 81/80, 126/125, 245/242, 385/384 | [⟨50 79 116 140 173]] | +1.54 | 1.63 | 6.76 |
| 2.3.5.7.11.13 | 81/80, 105/104, 126/125, 144/143, 245/242 | [⟨50 79 116 140 173 185]] | +1.31 | 1.57 | 6.54 |
Commas
50et tempers out the following commas. This assumes the val ⟨50 79 116 140 173 185 204 212 226], comma values in cents rounded to 2 decimal places. This list is not all-inclusive, and is based on the interval table from Scala version 2.2.
| Prime limit |
Ratio[note 2] | Monzo | Cents | Name |
|---|---|---|---|---|
| 3 | (20 digits) | [-79 50⟩ | 297.75 | 50-comma |
| 5 | 81/80 | [-4 4 -1⟩ | 21.51 | Syntonic comma |
| 5 | (20 digits) | [-27 -2 13⟩ | 18.17 | Ditonma |
| 5 | (20 digits) | [23 6 -14⟩ | 3.34 | Vishnuzma |
| 7 | 59049/57344 | [-13 10 0 -1⟩ | 50.72 | Harrison's comma |
| 7 | 16807/16384 | [-14 0 0 5⟩ | 44.13 | Cloudy comma |
| 7 | 3645/3584 | [-9 6 1 -1⟩ | 29.22 | Schismean comma |
| 7 | 126/125 | [1 2 -3 1⟩ | 13.79 | Starling comma |
| 7 | 225/224 | [-5 2 2 -1⟩ | 7.71 | Marvel comma |
| 7 | 3136/3125 | [6 0 -5 2⟩ | 6.08 | Hemimean comma |
| 7 | (24 digits) | [11 -10 -10 10⟩ | 5.57 | Linus comma |
| 7 | (12 digits) | [-11 2 7 -3⟩ | 1.63 | Meter |
| 7 | (12 digits) | [-6 -8 2 5⟩ | 1.12 | Wizma |
| 11 | 245/242 | [-1 0 1 2 -2⟩ | 21.33 | Frostma |
| 11 | 385/384 | [-7 -1 1 1 1⟩ | 4.50 | Keenanisma |
| 11 | 540/539 | [2 3 1 -2 -1⟩ | 3.21 | Swetisma |
| 11 | 4000/3993 | [5 -1 3 0 -3⟩ | 3.03 | Wizardharry comma |
| 11 | 9801/9800 | [-3 4 -2 -2 2⟩ | 0.18 | Kalisma |
| 13 | 105/104 | [-3 1 1 1 0 -1⟩ | 16.57 | Animist comma |
| 13 | 144/143 | [4 2 0 0 -1 -1⟩ | 12.06 | Grossma |
| 13 | 196/195 | [2 -1 -1 2 0 -1⟩ | 8.86 | Mynucuma |
| 13 | 1188/1183 | [2 3 0 -1 1 -2⟩ | 7.30 | Kestrel comma |
| 13 | 31213/31104 | [-7 -5 0 4 0 1⟩ | 6.06 | Praveensma |
| 13 | 364/363 | [2 -1 0 1 -2 1⟩ | 4.76 | Minor minthma |
| 13 | 2200/2197 | [3 0 2 0 1 -3⟩ | 2.36 | Petrma |
| 17 | 170/169 | [1 0 1 0 0 -2 1⟩ | 10.21 | Major naiadma |
| 17 | 221/220 | [-2 0 -1 0 -1 1 1⟩ | 7.85 | Minor naiadma |
| 17 | 289/288 | [-5 -2 0 0 0 0 2⟩ | 6.00 | Semitonisma |
| 17 | 375/374 | [-1 1 3 0 -1 0 -1⟩ | 4.62 | Ursulisma |
| 19 | 153/152 | [-3 2 0 0 0 0 1 -1⟩ | 11.35 | Ganassisma |
| 19 | 171/170 | [-1 2 -1 0 0 0 -1 1⟩ | 10.15 | Malcolmisma |
| 19 | 210/209 | [1 1 1 1 -1 0 0 1⟩ | 8.26 | Spleen comma |
| 19 | 324/323 | [2 4 0 0 0 0 -1 -1⟩ | 5.35 | Photisma |
| 19 | 361/360 | [-3 -2 -1 0 0 0 0 2⟩ | 4.80 | Go comma |
| 19 | 495/494 | [-1 2 1 0 1 -1 0 -1⟩ | 3.50 | Eulalisma |
| 23 | 507/506 | 2.3.11.13.23 [-1 1 -1 2 -1⟩ | 3.42 | Laodicisma |
| 23 | 529/528 | 2.3.11.23 [-4 -1 -1 2⟩ | 3.28 | Preziosisma |
| 23 | 576/575 | 2.3.5.23 [6 2 -2 -1⟩ | 3.01 | Worcester comma |
| 23 | 1288/1287 | [3 -2 0 1 -1 -1 0 0 1⟩ | 1.34 | Triaphonisma |
Rank-2 temperaments
| Periods per 8ve |
Generator* | Cents* | Associated ratio* |
Temperament |
|---|---|---|---|---|
| 1 | 1\50 | 24.0 | 686/675 | Sengagen |
| 1 | 9\50 | 216.0 | 17/15 | Tremka |
| 1 | 11\50 | 264.0 | 7/6 | Septimin |
| 1 | 13\50 | 312.0 | 6/5 | Oolong |
| 1 | 17\50 | 408.0 | 325/256 | Coditone |
| 1 | 19\50 | 456.0 | 125/96 | Qak |
| 1 | 21\50 | 504.0 | 4/3 | Meantone / meanpop |
| 1 | 23\50 | 552.0 | 11/8 | Emka |
| 2 | 2\50 | 48.0 | 36/35 | Pombe |
| 2 | 3\50 | 72.0 | 25/24 | Vishnu / vishnean |
| 2 | 6\50 | 144.0 | 12/11 | Bisemidim |
| 2 | 9\50 | 216.0 | 17/15 | Wizard / lizard / gizzard |
| 2 | 12\50 | 288.0 | 13/11 | Vines |
| 2 | 21\50 (4\50) |
504.0 (96.0) |
4/3 (35/33) |
Bimeantone |
| 5 | 21\50 (1\50) |
504.0 (24.0) |
4/3 (49/48) |
Cloudtone |
| 5 | 23 (3\50) |
552.0 (72.0) |
11/8 (21/20) |
Coblack |
| 10 | 7\50 (3\50) |
168.0 (72.0) |
54/49 (25/24) |
Decavish |
| 10 | 21\50 (1\50) |
504.0 (24.0) |
4/3 (78/77) |
Decic |
* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct
Instruments
- Lumatone
See Lumatone mapping for 50edo
- Piano
A piano playing with a 50edo ensemble may wish to use the tuning 116ed5. This tuning is almost exactly the same as 50edo, but with octaves stretched by 1 cent. Because pianos usually use stretched octaves, this tuning will sit better with the timbre of the piano, while still being close enough that it sounds perfectly in-tune with the other instruments tuned to 50edo.
Music
Modern renderings
- "Ricercar a 3" from The Musical Offering, BWV 1079 (1747) – rendered by Claudi Meneghin (2024)
- "Contrapunctus 4" from The Art of Fugue, BWV 1080 (1742–1749) – rendered by Claudi Meneghin (2024)
- "Contrapunctus 11" from The Art of Fugue, BWV 1080 (1742–1749) – rendered by Claudi Meneghin (2024, organ sound rendering)
- "Contrapunctus 11" from The Art of Fugue, BWV 1080 (1742-1749) — rendered by Claudi Meneghin (2025, harpsichord sound rendering)
- Prelude in E Minor "The Great" – rendered by Claudi Meneghin (2023)
- Pavane, op. 50 (1887) – arranged for harpsichord and rendered by Claudi Meneghin (2020)
- funfunfun ta yo (2007) – rendered by MortisTheneRd (2024)
21st century
- microtonal improv in 50edo (2024)
- Piano that may not be played that well - Deltarune (microtonal cover in 50edo) (2025)
- On My Way To Somewhere (2023)
- Twinkle canon – 50 edo [dead link]
- Blue Fugue for Organ (2018)
- La Petite Poule Grise - Fugue (2019)
- Happy Birthday Canon, 6-in-1 Canon in 50edo (2019)
- Fantasia Catalana (2020)
- Preludi Nocturn i Fuga sobre la Lluna la Pruna (2020)
- Fugue on the Dragnet theme (2020)
- Canon at the Semitone on The Mother's Malison Theme, for Organ (2022)
- Fugue on an Original Theme, for Baroque Ensemble (2023) (for Organ)
- Catalan Fugue (La Santa Espina) (2023)
- Canon in C= for Baroque Wind Ensemble (2023)
- Fantasia Catalana, for Baroque Ensemble (2023)
- the late little xmas album (2014)
- Harpsichord meantone improvisation 1 in 50EDO (2014)
- Long improvisation 2 in 50EDO (2014)
- Chord sequence for Difference tones in 50EDO (2014)
- Enharmonic Modulations in 50EDO (2014)
- Harmonic Clusters on 50EDO Harpsichord (2014)
- Fragment in Fifty (2014)
Additional reading
- Robert Smith's book online
- More information about Robert Smith's temperament[dead link]
- 50EDO Theory - Intervals, Chords and Scales in 50EDO by Cam Taylor[dead link]
- iamcamtaylor - Blog on 50EDO and extended meantone theory by Cam Taylor