13edo: Difference between revisions
No edit summary |
New harmonics template, lowercase edo, marked 16 dead links, misc. edits |
||
| Line 14: | Line 14: | ||
}} | }} | ||
''' | '''13 equal divisions of the octave''' ('''13edo''') is a tuning system which divides the [[octave]] into 13 equal parts of approximately 92.3 [[cent]]s each. It is the sixth [[prime edo]], following [[11edo]] and coming before [[17edo]]. The steps less than 600¢ are narrower than their nearest 12edo approximation, while those greater than 600¢ are wider. This allows for some neat ear-bending tricks, whereby melodic gestures reminiscent of 12edo can quickly arrive at an unfamiliar place. | ||
== Theory == | == Theory == | ||
{{ | {{Harmonics in equal|13}} | ||
As a temperament of 21-odd-limit | As a temperament of [[21-odd-limit]] [[just intonation]], 13edo has excellent approximations to the 11th and 21st [[harmonic]]s, and reasonable approximations to the 5th, 9th, 13th, 17th, and 19th harmonics. For most purposes it does not offer acceptable approximations to the 3rd, 7th, or 15th. The lack of reasonable approximation to the 3rd harmonic makes 13edo unsuitable for common-practice music, but its good approximations to ratios of 11, 13, and 21 make it a very xenharmonic tuning, as these identities are not remotely represented in 12edo. Despite its reputation for dissonance, it is an excellent rank-1 subgroup temperament, with the '''2.5.9.11.13.17.19.21''' subgroup being a particularly good example. It has a substantial repertoire of complex consonances for its small size. | ||
{| class="wikitable center-all right-2" | {| class="wikitable center-all right-2" | ||
| Line 25: | Line 25: | ||
! Degree | ! Degree | ||
! Cents | ! Cents | ||
! Approximated 21-limit Ratios<ref>Ratios are based on treating | ! Approximated 21-limit Ratios<ref>Ratios are based on treating 13edo as a 2.5.9.11.13.21 subgroup temperament; other approaches are possible.</ref> | ||
! [[Erv Wilson's Linear Notations|Erv Wilson]] | ! [[Erv Wilson's Linear Notations|Erv Wilson]] | ||
! Archaeotonic | ! Archaeotonic | ||
! Oneirotonic | ! Oneirotonic | ||
! [[26edo | ! [[26edo]] names | ||
! Fox-Raven Notation (J = 360Hz) | ! Fox-Raven Notation (J = 360Hz) | ||
! Pseudo-Diatonic Category | ! Pseudo-Diatonic Category | ||
| Line 175: | Line 175: | ||
<references/> | <references/> | ||
13edo can also be notated with ups and downs. The notational 5th is the 2nd-best approximation of 3/2, 7\13. This is 56¢ flat of 3/2, and the best approximation is 36¢ sharp, noticeably better. But using the 2nd-best 5th allows conventional notation to be used, including the staff, note names, relative notation, etc. There are two ways to do this. The first way preserves the <u>melodic</u> meaning of sharp/flat, major/minor and aug/dim, in that sharp is higher pitched than flat, and major/aug is wider than minor/dim. The disadvantage to this approach is that conventional interval arithmetic no longer works. e.g. M2 + M2 isn't M3, and D + M2 isn't E. Chord names are different because C - E - G isn't P1 - M3 - P5. | |||
The second approach preserves the <u>harmonic</u> meaning of sharp/flat, major/minor and aug/dim, in that the former is always further fifthwards on the chain of fifths than the latter. Sharp is lower in pitch than flat, and major/aug is narrower than minor/dim. While this approach may seem bizarre at first, interval arithmetic and chord names work as usual. Furthermore, conventional | The second approach preserves the <u>harmonic</u> meaning of sharp/flat, major/minor and aug/dim, in that the former is always further fifthwards on the chain of fifths than the latter. Sharp is lower in pitch than flat, and major/aug is narrower than minor/dim. While this approach may seem bizarre at first, interval arithmetic and chord names work as usual. Furthermore, conventional 12edo music can be directly translated to 13edo "on the fly". | ||
{| class="wikitable center-all right-2" | {| class="wikitable center-all right-2" | ||
| Line 345: | Line 345: | ||
genchain of seconds: ...d6 - d7 - d8 - d2 - m3 - m4 - m5 - m6 - P7 - P1 - P2 - M3 - M4 - M5 - M6 - A7 - A1 - A2 - A3... | genchain of seconds: ...d6 - d7 - d8 - d2 - m3 - m4 - m5 - m6 - P7 - P1 - P2 - M3 - M4 - M5 - M6 - A7 - A1 - A2 - A3... | ||
[[:File:13edo-chromatic-scale.mid| | [[:File:13edo-chromatic-scale.mid|13edo chromatic ascending and descending scale on C (MIDI)]] | ||
[[File:13_Edo_chromatic_scale_on_J.mp3]] | [[File:13_Edo_chromatic_scale_on_J.mp3]] | ||
| Line 354: | Line 354: | ||
== Tuning by ear == | == Tuning by ear == | ||
13edo can be approximated by a circle of [[64/49]] subminor fourths (which can be tuned by tuning two [[7/4]] subminor sevenths). A stack of 13 of these subfourths closes with an error of +10.526432¢, or +11% of 13-edo's step size. | |||
== Scales in | == Scales in 13edo == | ||
:''Main article: [[13edo | :''Main article: [[13edo scales]]'' | ||
Important MOSes (values in parentheses are (''period'', ''generator'')): | Important MOSes (values in parentheses are (''period'', ''generator'')): | ||
| Line 364: | Line 364: | ||
* [[Chromatic_pairs#Lovecraft|lovecraft]] [[4L 5s]] 212121211 (3\13, 1\1) | * [[Chromatic_pairs#Lovecraft|lovecraft]] [[4L 5s]] 212121211 (3\13, 1\1) | ||
* [[Chromatic_pairs#Sephiroth|Sephiroth]] [[3L 4s]] 3131311 (4\13, 1\1) | * [[Chromatic_pairs#Sephiroth|Sephiroth]] [[3L 4s]] 3131311 (4\13, 1\1) | ||
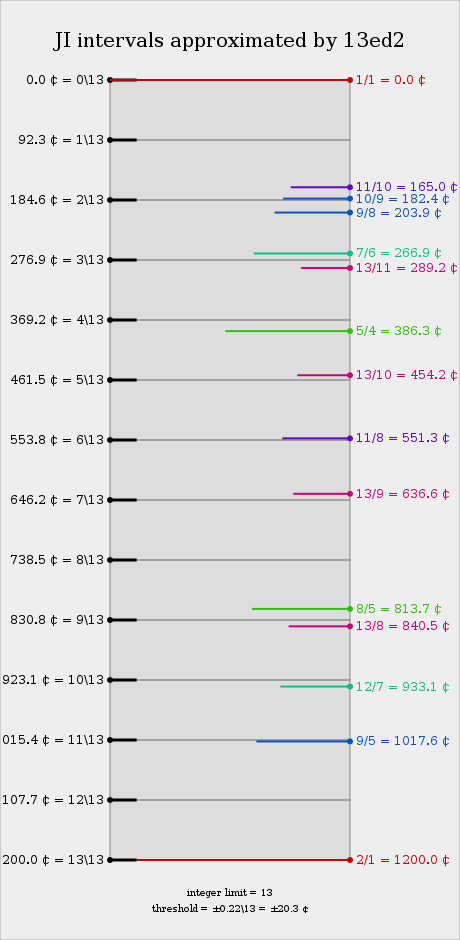
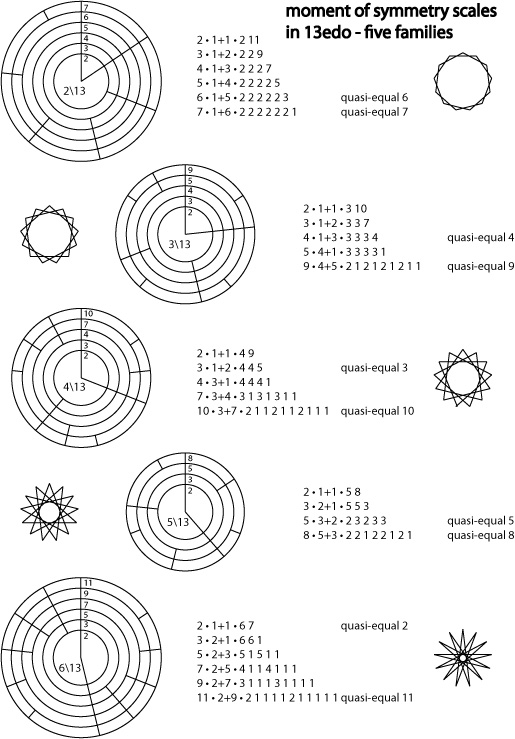
Due to the prime character of the number 13, | Due to the prime character of the number 13, 13edo can form several xenharmonic [[MOSScales|moment of symmetry scales]]. The diagram below shows five "families" of MOS scales: those generated by making a chain of 2\13 (two [[degree]]s of 13edo), 3\13, 4\13, 5\13, & 6\13, respectively. | ||
[[File:13edo_horograms.jpg|alt=13edo_horograms.jpg|13edo_horograms.jpg]] | [[File:13edo_horograms.jpg|alt=13edo_horograms.jpg|13edo_horograms.jpg]] | ||
| Line 372: | Line 372: | ||
~diagram by Andrew Heathwaite, based on horagrams pioneered by Erv Wilson | ~diagram by Andrew Heathwaite, based on horagrams pioneered by Erv Wilson | ||
Another neat facet of | Another neat facet of 13edo is the fact that any 12edo scale can be "turned into" a 13edo scale by either adding an extra semitone, or turning an existent semitone into a whole-tone. Because of this, melody in 13edo can be quite mind-bending and uncanny, and phrases that begin in a familiar way quickly lead to something totally unexpected. | ||
=== Pathological Modes === | === Pathological Modes === | ||
| Line 381: | Line 381: | ||
2 1 1 1 1 1 1 1 1 1 1 1 [[1L 11s]] MOS | 2 1 1 1 1 1 1 1 1 1 1 1 [[1L 11s]] MOS | ||
== Harmony in | == Harmony in 13edo == | ||
Contrary to popular belief, consonant harmony is possible in | Contrary to popular belief, consonant harmony is possible in 13edo, but it requires a radically different approach than that used in 12edo (or other Pythagorean or Meantone-based tunings). Trying to approximate the usual major and minor triads of 12edo within 13edo is usually a disappointment if consonance is the goal; 0-3-7, 0-4-7, 0-3-8, and 0-4-8 are all rather rough in 13edo. Typically, the most consonant harmonies do not use a "stack of 3rds" the way they do in 12edo, since the strongest dissonances in 13edo are near the middle of the octave (<u>[[13edo#top|degree]]s</u> 6, 7, and 8). Instead, a stack of whole-tones, or a mixture of whole-tones and minor 3rds, often yields good results. For example, one way to view 13edo is as a subgroup temperament of harmonics 2.5.9.11.13. It actually performs quite admirably in this regard, and a chord of 0-4-15-19-22 (approximating 4:5:9:11:13) sounds very convincing. An even larger subgroup is the [[k*N_subgroups|2*13 subgroup]] 2.9.5.21.11.13, on which 13 has the same tuning and commas as 26edo. | ||
By this, we can assume that the major ninth of | By this, we can assume that the major ninth of 13edo can be thought of as analogous to the perfect fifth in 12edo and other meantone edos. This means that the major second or major ninth is the most consonant interval next to 2/1 in 13edo followed by 11/8, 5/4 and so on. The 4:5:9 chord can therefore be thought of as a possible basic harmonic triad in 13edo. | ||
The 2.9.5.11.13 subgroup has commas 45/44, 65/64 and 81/80, leading to a linear temperament with POTE generator 185.728 cents, quite <u>[[13edo#top|close]]</u> to 2\13. Use this as a generator, and at 7 notes (6L 1s) two full pentads are available (as well as two more 4:5:9:11 tetrad, and one 4:5:9:13 tetrad). These triads and tetrads are likely the most consonant base sonorities available in | The 2.9.5.11.13 subgroup has commas 45/44, 65/64 and 81/80, leading to a linear temperament with POTE generator 185.728 cents, quite <u>[[13edo#top|close]]</u> to 2\13. Use this as a generator, and at 7 notes (6L 1s) two full pentads are available (as well as two more 4:5:9:11 tetrad, and one 4:5:9:13 tetrad). These triads and tetrads are likely the most consonant base sonorities available in 13edo and act in a similar way to major/minor triads. However, other sonorities such as Orwell chords are available as well. | ||
Other approaches explored by specific composers and theorists are outlined further down, in the context of more complete tonal systems. | Other approaches explored by specific composers and theorists are outlined further down, in the context of more complete tonal systems. | ||
| Line 406: | Line 406: | ||
[[File:13_edo_45921_chord.mp3]] | [[File:13_edo_45921_chord.mp3]] | ||
== Notational and Compositional Approaches to | == Notational and Compositional Approaches to 13edo == | ||
13edo has drawn the attention of numerous composers and theorists, some of whom have devoted some effort to provide a notation and an outline of a compositional approach to it. Some of these are described below. | |||
=== The Cryptic Ruse Methods === | === The Cryptic Ruse Methods === | ||
13edo offers two main candidates for diatonic-like scales: the 6L 1s heptatonic MOS generated by 2\13, and the 5L 3s octatonic MOS. Both of these scales are [[Rothenberg propriety|Rothenberg proper]], and bear a slightly-twisted resemblance to the 12edo diatonic scale. Specifically, the 6L 1s scale resembles the 12edo diatonic with one of its semitones replaced with a whole-tone, while the 5L 3s scale resembles the 12edo diatonic with an extra semitone inserted between two adjacent whole-tones. | |||
To facilitate discussion of these scales, [[Cryptic Ruse]] has ascribed them names based on H.P. Lovecraft's "Dream Cycle" mythos. | To facilitate discussion of these scales, [[Cryptic Ruse]] has ascribed them names based on H.P. Lovecraft's "Dream Cycle" mythos. | ||
| Line 417: | Line 417: | ||
The 2\13-based heptatonic has been named '''archeotonic''' after the "Old Ones" that rule the Dreamlands. Modes of the archeotonic are named after the individual Old Ones. | The 2\13-based heptatonic has been named '''archeotonic''' after the "Old Ones" that rule the Dreamlands. Modes of the archeotonic are named after the individual Old Ones. | ||
A 7-nominal notation is proposed, using the letters A-G. The "C natural" scale is proposed to be degrees 0-2-4-6-8-10-12-(13), with the note "C" tuned to a reference pitch of concert middle C. The modes are laid out in the following table, excerpted from an unfinished paper on 13- | A 7-nominal notation is proposed, using the letters A-G. The "C natural" scale is proposed to be degrees 0-2-4-6-8-10-12-(13), with the note "C" tuned to a reference pitch of concert middle C. The modes are laid out in the following table, excerpted from an unfinished paper on 13-edo. | ||
[[File:Archeotonic.png|alt=Archeotonic.png|Archeotonic.png]] | [[File:Archeotonic.png|alt=Archeotonic.png|Archeotonic.png]] | ||
Treating | Treating 13edo as a temperament as proposed above leads to a chord of degrees 0-2-4-6-9 representing the JI harmony 8:9:10:11:13; two such pentads exist in this scale, on E and F. Smaller harmonic units exist as follows: 8:9:10:11 on C, D, E, and F; 8:9:10:13 on E, F and G; 8:9:10 on C, D, E, F, and G; 8:9:11 on C, D, E, and F; 8:9:13 on E, F, G, and A. Finally, on B we have the relatively-discordant 16:17:21:26 (0-1-5-9, or the notes B-C-E-G), which can be octave-inverted into a more concordant 8:13:17:21. | ||
There may be other concordant harmonies possible in this scale that do not represent segments of the overtone series; further exploration is pending. | There may be other concordant harmonies possible in this scale that do not represent segments of the overtone series; further exploration is pending. | ||
| Line 428: | Line 428: | ||
The 5\13-based octatonic has been named '''[[oneirotonic]]''' after the Dreamlands themselves. Modes of the oneirotonic are named after cities in the Dreamlands. | The 5\13-based octatonic has been named '''[[oneirotonic]]''' after the Dreamlands themselves. Modes of the oneirotonic are named after cities in the Dreamlands. | ||
Here an 8-nominal notation is proposed, using letters A-H. The "C natural" scale is proposed to be degrees 0-2-4-5-7-9-10-12-(13), with the note "C" tuned to concert middle C. The modes are laid out in the following table, excerpted from an unfinished paper on | Here an 8-nominal notation is proposed, using letters A-H. The "C natural" scale is proposed to be degrees 0-2-4-5-7-9-10-12-(13), with the note "C" tuned to concert middle C. The modes are laid out in the following table, excerpted from an unfinished paper on 13edo. | ||
[[File:Oneirotonic.png|alt=Oneirotonic.png|Oneirotonic.png]] | [[File:Oneirotonic.png|alt=Oneirotonic.png|Oneirotonic.png]] | ||
| Line 435: | Line 435: | ||
=== Fox and Inthar's approach === | === Fox and Inthar's approach === | ||
Our approach is based on [[5L 3s]]. In fact, we have an absolute pitch notation for 5L 3s | Our approach is based on [[5L 3s]]. In fact, we have an absolute pitch notation for 5L 3s edos called the [[User:Inthar/Fox-Raven notation|Fox-Raven notation]]. | ||
== Mapping to Standard Keyboards == | == Mapping to Standard Keyboards == | ||
| Line 638: | Line 638: | ||
== Commas == | == Commas == | ||
13edo [[tempers out]] the following [[comma]]s. (Note: This assumes the [[val]] {{val| 13 21 30 36 45 48 }}.) | |||
{| class="commatable wikitable center-1 center-2 right-4 center-5" | {| class="commatable wikitable center-1 center-2 right-4 center-5" | ||
| Line 743: | Line 743: | ||
=== Animism === | === Animism === | ||
The animist comma, 105/104, appears whenever 3*5*7 = 2^3*13... | The animist comma, 105/104, appears whenever 3*5*7 = 2^3*13... 13edo does not approximate 3 and 7 individually (26edo does), but 13edo has 21/16 (21 = 3*7) and is also an animist temperament. In 13edo, the 5th harmonic is tuned so flatly that 5/4 = 16/13, leading to some interesting identities. So two scales stand out through this construction: | ||
0 4 5 8 9 13 pentatonic | 0 4 5 8 9 13 pentatonic | ||
| Line 752: | Line 752: | ||
== Introductory Materials == | == Introductory Materials == | ||
* [[File:13edo_1MC.mp3|270px]] | * [[File:13edo_1MC.mp3|270px]] 13edo example composition by [[User:IlL|Inthar]] ([[File:13edo_1MC_score.pdf|score]]) | ||
* [[File:13edo_Prelude_in_J_Oneirominor.mp3|Flute stop + harpsichord]] F# Oneirominor Prelude ([[:File:13edo_Prelude_in_J_Oneirominor Score.pdf|Score]]) | * [[File:13edo_Prelude_in_J_Oneirominor.mp3|Flute stop + harpsichord]] F# Oneirominor Prelude ([[:File:13edo_Prelude_in_J_Oneirominor Score.pdf|Score]]) | ||
* [[File:13edo_Fugue_in_J_Oneirominor chip.mp3|chiptune]] F# Oneirominor Fugue ([[:File:13edo_Fugue_in_J_Oneirominor Score.pdf|Score]]) | * [[File:13edo_Fugue_in_J_Oneirominor chip.mp3|chiptune]] F# Oneirominor Fugue ([[:File:13edo_Fugue_in_J_Oneirominor Score.pdf|Score]]) | ||
| Line 760: | Line 760: | ||
* [https://youtu.be/WWdbd877b54 Equilibrate] by [[Xotla]] | * [https://youtu.be/WWdbd877b54 Equilibrate] by [[Xotla]] | ||
* [https://youtu.be/x4Yesl8n6gc Brusselator Sprouts] by Xotla | * [https://youtu.be/x4Yesl8n6gc Brusselator Sprouts] by Xotla | ||
* [http://www.microtonalmusic.net/audio/slowdance13edo.mp3 Slow Dance] by [http://danielthompson.blogspot.com/ Daniel Thompson] | * [http://www.microtonalmusic.net/audio/slowdance13edo.mp3 Slow Dance]{{dead link}} by [http://danielthompson.blogspot.com/ Daniel Thompson] | ||
* [http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Hunt/Prelude%20in%2013ET.mp3 Prelude in 13ET] by [[Aaron Andrew Hunt]] - [http://soonlabel.com/xenharmonic/archives/2449 Organ version] {{dead link}} | * [http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Hunt/Prelude%20in%2013ET.mp3 Prelude in 13ET]{{dead link}} by [[Aaron Andrew Hunt]] - [http://soonlabel.com/xenharmonic/archives/2449 Organ version]{{dead link}} | ||
* [http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Hunt/13ET.mp3 Two-Part Invention in 13ET] by Aaron Andrew Hunt | * [http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Hunt/13ET.mp3 Two-Part Invention in 13ET]{{dead link}} by Aaron Andrew Hunt | ||
* [http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Herman/triskaidekaphobia.mp3 Triskaidekaphobia] by [http://soonlabel.com/xenharmonic/archives/2642 Herman Miller] - [http://soonlabel.com/xenharmonic/archives/2642 Baroque ensemble version] | * [http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Herman/triskaidekaphobia.mp3 Triskaidekaphobia]{{dead link}} by [http://soonlabel.com/xenharmonic/archives/2642 Herman Miller]{{dead link}} - [http://soonlabel.com/xenharmonic/archives/2642 Baroque ensemble version]{{dead link}} | ||
* [ | * [https://www.soundclick.com/music/songInfo.cfm?songID=835265 Spikey Hair in 13tET] [http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Heathwaite/andrewheathwaite+improvisationin13tet.mp3 play] by [[Andrew Heathwaite]] | ||
* [[:File:Fuzz_Reef.mp3|Fuzz Reef]] in Glacial[7] by [[Chuckles McGee]] | * [[:File:Fuzz_Reef.mp3|Fuzz Reef]] in Glacial[7] by [[Chuckles McGee]] | ||
* [[:File:Lunar_Approach.mp3|Lunar Approach]] in Father[8] by Chuckles McGee | * [[:File:Lunar_Approach.mp3|Lunar Approach]] in Father[8] by Chuckles McGee | ||
* [http://www.elvenminstrel.com/music/tuning/equal/13equal/13tet.htm Upsidedown and Backwards: Explorations in 13-tone Equal Temperament] by [http://www.elvenminstrel.com/ David J. Finnamore] | * [http://www.elvenminstrel.com/music/tuning/equal/13equal/13tet.htm Upsidedown and Backwards: Explorations in 13-tone Equal Temperament] by [http://www.elvenminstrel.com/ David J. Finnamore] | ||
* [http://micro.soonlabel.com/gene_ward_smith/Others/Winchester/11%20-%2011.%2013%20octave.mp3 Comets Over Flatland 11] by [[Randy Winchester]] | * [http://micro.soonlabel.com/gene_ward_smith/Others/Winchester/11%20-%2011.%2013%20octave.mp3 Comets Over Flatland 11]{{dead link}} by [[Randy Winchester]] | ||
* [http://archive.org/details/ineedSynthetiklove (iNeed) SyNthetikLove] [http://archive.org/download/ineedSynthetiklove/iNeed_SyNthetikLove.mp3 play] by [[Jon Lyle Smith]] | * [http://archive.org/details/ineedSynthetiklove (iNeed) SyNthetikLove]{{dead link}} [http://archive.org/download/ineedSynthetiklove/iNeed_SyNthetikLove.mp3 play]{{dead link}} by [[Jon Lyle Smith]] | ||
* [https://soundcloud.com/jonlylesmith/strange-strange-day Strange, Strange Day] [http://micro.soonlabel.com/gene_ward_smith/Others/Jlsimith/__Strange__Strange_Day_by_jonlylesmith.mp3 play] by Jon Lyle Smith | * [https://soundcloud.com/jonlylesmith/strange-strange-day Strange, Strange Day]{{dead link}} [http://micro.soonlabel.com/gene_ward_smith/Others/Jlsimith/__Strange__Strange_Day_by_jonlylesmith.mp3 play]{{dead link}} by Jon Lyle Smith | ||
* [https://soundcloud.com/jonlylesmith/stare-into-the-sun Stare (into The Sun)] [http://micro.soonlabel.com/gene_ward_smith/Others/Jlsimith/__Stare__into_The_Sun__by_jonlylesmith.mp3 play] by Jon Lyle Smith | * [https://soundcloud.com/jonlylesmith/stare-into-the-sun Stare (into The Sun)]{{dead link}} [http://micro.soonlabel.com/gene_ward_smith/Others/Jlsimith/__Stare__into_The_Sun__by_jonlylesmith.mp3 play]{{dead link}} by Jon Lyle Smith | ||
* [http://micro.soonlabel.com/13edo/20120225-midiaxe-prelude-for-synthesizer-in-13-equal.mp3 Prelude for Synthesizer in 13 Equal] by [[Chris Vaisvil]] | * [http://micro.soonlabel.com/13edo/20120225-midiaxe-prelude-for-synthesizer-in-13-equal.mp3 Prelude for Synthesizer in 13 Equal] by [[Chris Vaisvil]] | ||
* [http://micro.soonlabel.com/13edo/muon_catalyzed_fusion_13_edo.mp3 Muon Catalyzed Fusion] by Chris Vaisvil | * [http://micro.soonlabel.com/13edo/muon_catalyzed_fusion_13_edo.mp3 Muon Catalyzed Fusion] by Chris Vaisvil | ||
| Line 786: | Line 786: | ||
* [http://www.seraph.it/dep/det/Lotus13.mp3 Lotus 13] by Carlo Serafini ([http://www.seraph.it/blog_files/e63d2a478d5d422027d27eb6f9dc59f5-255.html blog entry]) | * [http://www.seraph.it/dep/det/Lotus13.mp3 Lotus 13] by Carlo Serafini ([http://www.seraph.it/blog_files/e63d2a478d5d422027d27eb6f9dc59f5-255.html blog entry]) | ||
* [http://soundcloud.com/xenvotta/sets/votta-liber-stellarum-for/ Liber Stellarum] by [http://votta.wordpress.com Alfredo Votta] | * [http://soundcloud.com/xenvotta/sets/votta-liber-stellarum-for/ Liber Stellarum] by [http://votta.wordpress.com Alfredo Votta] | ||
* [http://soonlabel.com/xenharmonic/wp-content/uploads/2014/02/Margo-Schulter-For_Claudi-2014-02-17-13edo.mp3 For Claudi] by [http://soonlabel.com/xenharmonic/archives/1788 Margo Schulter] | * [http://soonlabel.com/xenharmonic/wp-content/uploads/2014/02/Margo-Schulter-For_Claudi-2014-02-17-13edo.mp3 For Claudi]{{dead link}} by [http://soonlabel.com/xenharmonic/archives/1788 Margo Schulter]{{dead link}} | ||
* [https://youtu.be/7ohvxMjsuXs Autogynephilia by Diamond Doll] | * [https://youtu.be/7ohvxMjsuXs Autogynephilia by Diamond Doll] | ||
* [https://soundcloud.com/inthar-the-tergetian/a-moment-of-respite-wip A Moment Of Respite (WIP)] ([[:File:A Moment of Respite.mp3]]) by [[Inthar lus Lăneaf]] | * [https://soundcloud.com/inthar-the-tergetian/a-moment-of-respite-wip A Moment Of Respite (WIP)]{{dead link}} ([[:File:A Moment of Respite.mp3]]) by [[Inthar lus Lăneaf]] | ||
* [https://cityoftheasleep.bandcamp.com/track/wintermint-13edo Wintermint (13EDO)] by [[City of the Asleep]] | * [https://cityoftheasleep.bandcamp.com/track/wintermint-13edo Wintermint (13EDO)] by [[City of the Asleep]] | ||
* [https://cityoftheasleep.bandcamp.com/track/future-dust-13edo Future Dust (13EDO) | City of the Asleep] | * [https://cityoftheasleep.bandcamp.com/track/future-dust-13edo Future Dust (13EDO) | City of the Asleep] | ||
| Line 797: | Line 797: | ||
* [[Kentaku's_Approach_to_13EDO|William Lynch's 13 EDO octaton approach]] | * [[Kentaku's_Approach_to_13EDO|William Lynch's 13 EDO octaton approach]] | ||
* [[13EDO Scales and Chords for Guitar]] | * [[13EDO Scales and Chords for Guitar]] | ||
* [[Well-Tempered 13-Tone Clavier|The Well-Tempered 13-Tone Clavier]]: A collab project to create 26 preludes and 26 fugues, one in each | * [[Well-Tempered 13-Tone Clavier|The Well-Tempered 13-Tone Clavier]]: A collab project to create 26 preludes and 26 fugues, one in each 13edo key. | ||
[[Category:13-tone]] | [[Category:13-tone]] | ||
Revision as of 21:00, 15 January 2022
| ← 12edo | 13edo | 14edo → |
13 equal divisions of the octave (13edo) is a tuning system which divides the octave into 13 equal parts of approximately 92.3 cents each. It is the sixth prime edo, following 11edo and coming before 17edo. The steps less than 600¢ are narrower than their nearest 12edo approximation, while those greater than 600¢ are wider. This allows for some neat ear-bending tricks, whereby melodic gestures reminiscent of 12edo can quickly arrive at an unfamiliar place.
Theory
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +36.5 | -17.1 | -45.7 | -19.3 | +2.5 | -9.8 | +19.4 | -12.6 | -20.6 | -9.2 | +17.9 |
| Relative (%) | +39.5 | -18.5 | -49.6 | -20.9 | +2.7 | -10.6 | +21.0 | -13.7 | -22.3 | -10.0 | +19.4 | |
| Steps (reduced) |
21 (8) |
30 (4) |
36 (10) |
41 (2) |
45 (6) |
48 (9) |
51 (12) |
53 (1) |
55 (3) |
57 (5) |
59 (7) | |
As a temperament of 21-odd-limit just intonation, 13edo has excellent approximations to the 11th and 21st harmonics, and reasonable approximations to the 5th, 9th, 13th, 17th, and 19th harmonics. For most purposes it does not offer acceptable approximations to the 3rd, 7th, or 15th. The lack of reasonable approximation to the 3rd harmonic makes 13edo unsuitable for common-practice music, but its good approximations to ratios of 11, 13, and 21 make it a very xenharmonic tuning, as these identities are not remotely represented in 12edo. Despite its reputation for dissonance, it is an excellent rank-1 subgroup temperament, with the 2.5.9.11.13.17.19.21 subgroup being a particularly good example. It has a substantial repertoire of complex consonances for its small size.
| Degree | Cents | Approximated 21-limit Ratios[1] | Erv Wilson | Archaeotonic | Oneirotonic | 26edo names | Fox-Raven Notation (J = 360Hz) | Pseudo-Diatonic Category |
|---|---|---|---|---|---|---|---|---|
| 0 | 0.00 | 1/1 | H | C | C | C | J | Unison |
| 1 | 92.31 | 17/16, 18/17, 19/18, 20/19, 21/20, 22/21 | β | C#/Db | C#/Db | Cx/Dbb | J#/Kb | Minor second |
| 2 | 184.62 | 9/8, 10/9, 11/10, 19/17, 21/19 | A | D | D | D | K | Major second |
| 3 | 276.92 | 7/6, 13/11, 20/17, 19/16, 22/19 | δ | D#/Eb | D#/Eb | Dx/Ebb | L | Minor third |
| 4 | 369.23 | 5/4, 11/9, 16/13, 26/21 | C | E | E | E | L#/Mb | Major third |
| 5 | 461.54 | 13/10, 17/13, 21/16, 22/17 | B | E#/Fb | F | Ex/Fb | M | Minor fourth |
| 6 | 553.85 | 11/8, 18/13, 26/19 | ε | F | F#/Gb | F# | M#/Nb | Major fourth/Minor tritone |
| 7 | 646.15 | 16/11, 13/9, 19/13 | D | F#/Gb | G | Gb | N | Minor fifth/Major tritone |
| 8 | 738.46 | 17/11, 20/13, 26/17, 32/21 | γ | G | G#/Hb | G# | O | Major fifth |
| 9 | 830.77 | 8/5, 13/8, 18/11, 21/13 | F | G#/Ab | H | Ab | O#/Pb | Minor sixth |
| 10 | 923.08 | 17/10, 12/7, 22/13, 19/11 | E | A | A | A# | P | Major sixth |
| 11 | 1015.38 | 9/5, 16/9, 20/11, 34/19, 38/21 | α | A#/Bb | A#/Bb | Bb | Q | Minor seventh |
| 12 | 1107.69 | 17/9, 19/10, 21/11, 32/17, 36/19, 40/21 | G | B/Cb | B | B#/Cbb | Q#/Jb | Major seventh |
| 13 | 1200.00 | 2/1 | H | C/B# | C | C | J | Octave |
- ↑ Ratios are based on treating 13edo as a 2.5.9.11.13.21 subgroup temperament; other approaches are possible.
13edo can also be notated with ups and downs. The notational 5th is the 2nd-best approximation of 3/2, 7\13. This is 56¢ flat of 3/2, and the best approximation is 36¢ sharp, noticeably better. But using the 2nd-best 5th allows conventional notation to be used, including the staff, note names, relative notation, etc. There are two ways to do this. The first way preserves the melodic meaning of sharp/flat, major/minor and aug/dim, in that sharp is higher pitched than flat, and major/aug is wider than minor/dim. The disadvantage to this approach is that conventional interval arithmetic no longer works. e.g. M2 + M2 isn't M3, and D + M2 isn't E. Chord names are different because C - E - G isn't P1 - M3 - P5.
The second approach preserves the harmonic meaning of sharp/flat, major/minor and aug/dim, in that the former is always further fifthwards on the chain of fifths than the latter. Sharp is lower in pitch than flat, and major/aug is narrower than minor/dim. While this approach may seem bizarre at first, interval arithmetic and chord names work as usual. Furthermore, conventional 12edo music can be directly translated to 13edo "on the fly".
| Degree | Cents | Up/down notation using the narrow 5th of 7\13, with major wider than minor |
Up/down notation using the narrow 5th of 7\13, with major narrower than minor | ||||
|---|---|---|---|---|---|---|---|
| 0 | 0 | perfect unison | P1 | D | perfect unison | P1 | D |
| 1 | 92 | up unison, minor 2nd | ^1, m2 | ^D, E | up unison, major 2nd | ^1, M2 | ^D, E |
| 2 | 185 | upminor 2nd, minor 3rd | ^m2, m3 | ^E, Fb | upmajor 2nd, major 3rd | ^M2, M3 | ^E, F# |
| 3 | 277 | downmajor 2nd, upminor 3rd | vM2, ^m3 | vE#, ^Fb | downminor 2nd, upmajor 3rd | vm2, ^M3 | vEb, ^F# |
| 4 | 369 | major 2nd, downmajor 3rd | M2, vM3 | E#, vF | minor 2nd, downminor 3rd | m2, vm3 | Eb, vF |
| 5 | 462 | major 3rd, down 4th | M3, v4 | F, vG | minor 3rd, down 4th | m3, v4 | F, vG |
| 6 | 554 | perfect 4th, down 5th | P4, v5 | G, vA | perfect 4th, down 5th | P4, v5 | G, vA |
| 7 | 646 | up 4th, perfect 5th | ^4, P5 | ^G, A | up 4th, perfect 5th | ^4, P5 | ^G, A |
| 8 | 738 | up 5th, minor 6th | ^5, m6 | ^A, B | up 5th, major 6th | ^5, M6 | ^A, B |
| 9 | 831 | upminor 6th, minor 7th | ^m6, m7 | ^B, Cb | upmajor 6th, major 7th | ^M6, M7 | ^B, C# |
| 10 | 923 | downmajor 6th, upminor 7th | vM6, ^m7 | vB#, ^Cb | downminor 6th, upmajor 7th | vm6, ^M7 | vBb, ^C# |
| 11 | 1015 | major 6th, downmajor 7th | M6, vM7 | B#, vC | minor 6th, downminor 7th | m6, vm7 | Bb, vC |
| 12 | 1108 | major 7th, down 8ve | M7, v8 | C, vD | minor 7th, down 8ve | m7, v8 | C, vD |
| 13 | 1200 | perfect 8ve | P8 | D | perfect 8ve | P8 | D |
This is a heptatonic notation generated by 5ths (5th meaning 3/2). Alternative notations include pentatonic 5th-generated, octatonic 5th-generated, and heptatonic 2nd-generated.
Pentatonic 5th-generated: D * * E * G * * A * C * * D (generator = wide 3/2 = 8\13 = perfect 5thoid)
D - D# - Eb - E - E#/Gb - G - G# - Ab - A - A#/Cb - C - C# - Db - D
P1 - A1/ds3 - ms3 - Ms3 - As3/d4d - P4d - A4d - d5d - P5d - A5d/ds7 - ms7 - Ms7 - As7/d8d - P8d (s = sub-, d = -oid)
pentatonic genchain of fifths: ...Ebb - Cb - Gb - Db - Ab - Eb - C - G - D - A - E - C# - G# - D# - A# - E# - Cx...
pentatonic genchain of fifths: ...ds3 - ds7 - d4d - d8d - d5d - ms3 - ms7 - P4d - P1 - P5d - Ms3 - Ms7 - A4d - A1 - A5d - As3 - As7... (s = sub-, d = -oid)
Octatonic 5th-generated: A * B C * D * E F * G H * A (generator = wide 3/2 = 8\13 = perfect 6th)
A - A#/Bb - B - C - C#/Db - D - D#/Eb - E - F - F#/Gb - G - H - H#/Ab - A
P1 - m2 - M2 - m3 - M3 - P4 - m5 - M5 - P6 - m7 - M7 - m8 - M8 - P9
octotonic genchain of sixths: ..D# - A# - F# - C# - H# - E - B - G - D - A - F - C - H - Eb - Bb - Gb - Db - Ab...
octotonic genchain of sixths: ...M3 - M8 - M5 - M2 - M7 - P4 - P1 - P6 - m3 - m8 - m5 - m2 - m7...
Heptatonic 2nd-generated: D * E * F * G A * B * C * D (generator = 2\13 = perfect 2nd)
D - D#/Eb - E - E#/Fb - F - F#/Gb - G - A - A#/Bb - B - B#/Cb - C - C#/Db - D
P1 - A1/d2 - P2 - m3 - M3 - m4 - M4 - m5 - M5 - m6 - M6 - P7 - A7/d8 - P8
genchain of seconds: ...Ab - Bb - Cb - Db - Eb - Fb - Gb - A - B - C - D - E - F - G - A# - B# - C# - D# - E# - F# - G#...
genchain of seconds: ...d6 - d7 - d8 - d2 - m3 - m4 - m5 - m6 - P7 - P1 - P2 - M3 - M4 - M5 - M6 - A7 - A1 - A2 - A3...
13edo chromatic ascending and descending scale on C (MIDI)
Tuning by ear
13edo can be approximated by a circle of 64/49 subminor fourths (which can be tuned by tuning two 7/4 subminor sevenths). A stack of 13 of these subfourths closes with an error of +10.526432¢, or +11% of 13-edo's step size.
Scales in 13edo
- Main article: 13edo scales
Important MOSes (values in parentheses are (period, generator)):
- oneirotonic (A-Team/Petrtri) 5L 3s 22122121 (5\13, 1\1)
- archeotonic 6L 1s 2222221 (2\13, 1\1)
- lovecraft 4L 5s 212121211 (3\13, 1\1)
- Sephiroth 3L 4s 3131311 (4\13, 1\1)
Due to the prime character of the number 13, 13edo can form several xenharmonic moment of symmetry scales. The diagram below shows five "families" of MOS scales: those generated by making a chain of 2\13 (two degrees of 13edo), 3\13, 4\13, 5\13, & 6\13, respectively.
~diagram by Andrew Heathwaite, based on horagrams pioneered by Erv Wilson
Another neat facet of 13edo is the fact that any 12edo scale can be "turned into" a 13edo scale by either adding an extra semitone, or turning an existent semitone into a whole-tone. Because of this, melody in 13edo can be quite mind-bending and uncanny, and phrases that begin in a familiar way quickly lead to something totally unexpected.
Pathological Modes
2 1 1 1 1 2 1 1 1 1 1 2L 9s MOS
3 1 1 1 1 1 1 1 1 1 1 1L 10s MOS
2 1 1 1 1 1 1 1 1 1 1 1 1L 11s MOS
Harmony in 13edo
Contrary to popular belief, consonant harmony is possible in 13edo, but it requires a radically different approach than that used in 12edo (or other Pythagorean or Meantone-based tunings). Trying to approximate the usual major and minor triads of 12edo within 13edo is usually a disappointment if consonance is the goal; 0-3-7, 0-4-7, 0-3-8, and 0-4-8 are all rather rough in 13edo. Typically, the most consonant harmonies do not use a "stack of 3rds" the way they do in 12edo, since the strongest dissonances in 13edo are near the middle of the octave (degrees 6, 7, and 8). Instead, a stack of whole-tones, or a mixture of whole-tones and minor 3rds, often yields good results. For example, one way to view 13edo is as a subgroup temperament of harmonics 2.5.9.11.13. It actually performs quite admirably in this regard, and a chord of 0-4-15-19-22 (approximating 4:5:9:11:13) sounds very convincing. An even larger subgroup is the 2*13 subgroup 2.9.5.21.11.13, on which 13 has the same tuning and commas as 26edo.
By this, we can assume that the major ninth of 13edo can be thought of as analogous to the perfect fifth in 12edo and other meantone edos. This means that the major second or major ninth is the most consonant interval next to 2/1 in 13edo followed by 11/8, 5/4 and so on. The 4:5:9 chord can therefore be thought of as a possible basic harmonic triad in 13edo.
The 2.9.5.11.13 subgroup has commas 45/44, 65/64 and 81/80, leading to a linear temperament with POTE generator 185.728 cents, quite close to 2\13. Use this as a generator, and at 7 notes (6L 1s) two full pentads are available (as well as two more 4:5:9:11 tetrad, and one 4:5:9:13 tetrad). These triads and tetrads are likely the most consonant base sonorities available in 13edo and act in a similar way to major/minor triads. However, other sonorities such as Orwell chords are available as well.
Other approaches explored by specific composers and theorists are outlined further down, in the context of more complete tonal systems.
Play the 4:5:9 chord:
Play the 4:5:9:11 chord:
Play the 4:5:9:13 chord:
Play the 4:5:9:21 chord:
Notational and Compositional Approaches to 13edo
13edo has drawn the attention of numerous composers and theorists, some of whom have devoted some effort to provide a notation and an outline of a compositional approach to it. Some of these are described below.
The Cryptic Ruse Methods
13edo offers two main candidates for diatonic-like scales: the 6L 1s heptatonic MOS generated by 2\13, and the 5L 3s octatonic MOS. Both of these scales are Rothenberg proper, and bear a slightly-twisted resemblance to the 12edo diatonic scale. Specifically, the 6L 1s scale resembles the 12edo diatonic with one of its semitones replaced with a whole-tone, while the 5L 3s scale resembles the 12edo diatonic with an extra semitone inserted between two adjacent whole-tones.
To facilitate discussion of these scales, Cryptic Ruse has ascribed them names based on H.P. Lovecraft's "Dream Cycle" mythos.
Modes and Harmony in the Archeotonic Scale
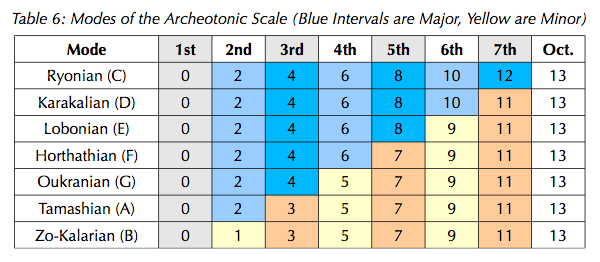
The 2\13-based heptatonic has been named archeotonic after the "Old Ones" that rule the Dreamlands. Modes of the archeotonic are named after the individual Old Ones.
A 7-nominal notation is proposed, using the letters A-G. The "C natural" scale is proposed to be degrees 0-2-4-6-8-10-12-(13), with the note "C" tuned to a reference pitch of concert middle C. The modes are laid out in the following table, excerpted from an unfinished paper on 13-edo.
Treating 13edo as a temperament as proposed above leads to a chord of degrees 0-2-4-6-9 representing the JI harmony 8:9:10:11:13; two such pentads exist in this scale, on E and F. Smaller harmonic units exist as follows: 8:9:10:11 on C, D, E, and F; 8:9:10:13 on E, F and G; 8:9:10 on C, D, E, F, and G; 8:9:11 on C, D, E, and F; 8:9:13 on E, F, G, and A. Finally, on B we have the relatively-discordant 16:17:21:26 (0-1-5-9, or the notes B-C-E-G), which can be octave-inverted into a more concordant 8:13:17:21.
There may be other concordant harmonies possible in this scale that do not represent segments of the overtone series; further exploration is pending.
Modes and Harmony in the Oneirotonic Scale
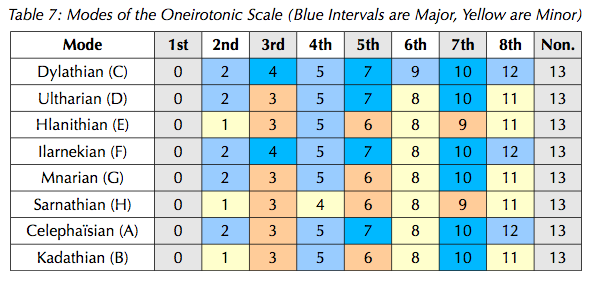
The 5\13-based octatonic has been named oneirotonic after the Dreamlands themselves. Modes of the oneirotonic are named after cities in the Dreamlands.
Here an 8-nominal notation is proposed, using letters A-H. The "C natural" scale is proposed to be degrees 0-2-4-5-7-9-10-12-(13), with the note "C" tuned to concert middle C. The modes are laid out in the following table, excerpted from an unfinished paper on 13edo.
There is a great number of potential consonant harmonies in this scale. A dedicated article on harmony and tonality in the oneirotonic scale is forthcoming.
Fox and Inthar's approach
Our approach is based on 5L 3s. In fact, we have an absolute pitch notation for 5L 3s edos called the Fox-Raven notation.
Mapping to Standard Keyboards
The 5L+3s scale (Oneirotonic) can be mapped to the standard keyboard effectively, although somewhat awkwardly. Consider the sequence of 730-cent intervals that it derives from: 1 6 11 3 8 (13) 5 10 2 7 12 4 9 1/1. One of these must be absent, so it might as well be the last. So, there are at most five of the full octatonic scales on different keys. Of the four mappings that keep the major pentatonic on the white keys, which ironically look like ordinary minor-pentatonics, the latter which begins on B might be the most straightforward to learn and use.
| 1 | 6 | 11 | 3 | 8 | (13) | 5 | 10 | 2 | 7 | 12 | 4 | 9 | 1 | Place in Chain of 738.5 cent intervals |
| X | * | * | * | * | * | * | * | X | Marked are the octatonic scales (X=Sarnathian) | |||||
| * | * | * | * | X | * | * | * | |||||||
| * | X | * | * | * | * | * | * | |||||||
| * | * | * | * | * | * | X | * | |||||||
| * | * | * | X | * | * | * | * | |||||||
| D | Eb | E | F | Gb | G | Ab | A | Bb | B | C | Db | D | Keeps the pentatonic scale on the white keys | |
| A | Bb | B | C | Db | D | Eb | E | F | Gb | G | Ab | A | ||
| E | F | Gb | G | Ab | A | Bb | B | C | Db | D | Eb | E | ||
| B | C | Db | D | Eb | E | F | Gb | G | Ab | A | Bb | B | ||
| C | Db | D | Eb | E | F | Gb | G | Ab | A | Bb | B | C | Puts the missing key between a semitone | |
| G | Ab | A | Bb | B | C | Db | D | Eb | E | F | Gb | G | (if that were to be valuable in any way) |
The archaeotonic tonality is much simpler to deal with: you just leave out a tone and remember which one. Although, for diatonic use it may be more convenient to put the missing tone between E/F or B/C to keep it on the white keys, with the remaining small step where it looks like it should be.
Commas
13edo tempers out the following commas. (Note: This assumes the val ⟨13 21 30 36 45 48].)
| Prime limit |
Ratio[1] | Monzo | Cents | Color name | Name(s) |
|---|---|---|---|---|---|
| 5 | (14 digits) | [-21 3 7⟩ | 10.06 | Lasepyo | Semicomma, Fokker comma |
| 7 | 1029/1000 | [-3 1 -3 3⟩ | 49.49 | Trizogu | Keega |
| 7 | 525/512 | [-9 1 2 1⟩ | 43.41 | Lazoyoyo | Avicennma, Avicenna's Enharmonic Diesis |
| 7 | 64/63 | [6 -2 0 -1⟩ | 27.26 | Ru | Septimal Comma, Archytas' Comma, Leipziger Komma |
| 7 | 64827/64000 | [-9 3 -3 4⟩ | 22.23 | Laquadzo-atrigu | Squalentine |
| 7 | 3125/3087 | [0 -2 5 -3⟩ | 21.18 | Triru-aquinyo | Gariboh |
| 7 | 3136/3125 | [6 0 -5 2⟩ | 6.08 | Zozoquingu | Hemimean comma |
| 11 | 56/55 | [3 0 -1 1 -1⟩ | 31.19 | Luzogu | Undecimal diesis |
| 11 | 121/120 | [-3 -1 -1 0 2⟩ | 14.37 | Lologu | Biyatisma |
| 11 | 441/440 | [-3 2 -1 2 -1⟩ | 3.93 | Luzozogu | Werckisma |
| 13 | 40/39 | [3 -1 1 0 0 -1⟩ | 43.83 | Thuyo | Tridecimal minor diesis |
| 13 | 105/104 | [-3 1 1 1 0 -1⟩ | 16.57 | Thuzoyo | Animist |
| 13 | 169/168 | [-3 -1 0 -1 0 2⟩ | 10.27 | Thothoru | Buzurgisma |
- ↑ Ratios longer than 10 digits are presented by placeholders with informative hints
Animism
The animist comma, 105/104, appears whenever 3*5*7 = 2^3*13... 13edo does not approximate 3 and 7 individually (26edo does), but 13edo has 21/16 (21 = 3*7) and is also an animist temperament. In 13edo, the 5th harmonic is tuned so flatly that 5/4 = 16/13, leading to some interesting identities. So two scales stand out through this construction:
0 4 5 8 9 13 pentatonic
and
0 1 3 4 5 8 9 10 12 13 nonatonic
Introductory Materials
- 13edo example composition by Inthar (File:13edo 1MC score.pdf)
- F# Oneirominor Prelude (Score)
- F# Oneirominor Fugue (Score)
Music
- Equilibrate by Xotla
- Brusselator Sprouts by Xotla
- Slow Dance[dead link] by Daniel Thompson
- Prelude in 13ET[dead link] by Aaron Andrew Hunt - Organ version[dead link]
- Two-Part Invention in 13ET[dead link] by Aaron Andrew Hunt
- Triskaidekaphobia[dead link] by Herman Miller[dead link] - Baroque ensemble version[dead link]
- Spikey Hair in 13tET play by Andrew Heathwaite
- Fuzz Reef in Glacial[7] by Chuckles McGee
- Lunar Approach in Father[8] by Chuckles McGee
- Upsidedown and Backwards: Explorations in 13-tone Equal Temperament by David J. Finnamore
- Comets Over Flatland 11[dead link] by Randy Winchester
- (iNeed) SyNthetikLove[dead link] play[dead link] by Jon Lyle Smith
- Strange, Strange Day[dead link] play[dead link] by Jon Lyle Smith
- Stare (into The Sun)[dead link] play[dead link] by Jon Lyle Smith
- Prelude for Synthesizer in 13 Equal by Chris Vaisvil
- Muon Catalyzed Fusion by Chris Vaisvil
- 13 Miles by Carlo Serafini (blog entry)
- Fast And Furious 13 by Carlo Serafini (blog entry)
- SazDul 13 by Carlo Serafini (blog entry)
- Thirteenstan by Carlo Serafini (blog entry)
- Concertina 13 by Carlo Serafini (blog entry)
- Hocus-Bogus 13 by Carlo Serafini (blog entry)
- MP13 by Carlo Serafini (blog entry)
- Berimbau 13 by Carlo Serafini (blog entry)
- Tenori Blofeld (video) by Carlo Serafini (blog entry)
- From The Diary Of The 13th Fly by Carlo Serafini (blog entry)
- Lotus 13 by Carlo Serafini (blog entry)
- Liber Stellarum by Alfredo Votta
- For Claudi[dead link] by Margo Schulter[dead link]
- Autogynephilia by Diamond Doll
- A Moment Of Respite (WIP)[dead link] (File:A Moment of Respite.mp3) by Inthar lus Lăneaf
- Wintermint (13EDO) by City of the Asleep
- Future Dust (13EDO) | City of the Asleep
- Fugitive from Sleep (13EDO) | City of the Asleep
- Study in a newly discovered 13-ET scale by Yin Bell
See also
- William Lynch's 13 EDO octaton approach
- 13EDO Scales and Chords for Guitar
- The Well-Tempered 13-Tone Clavier: A collab project to create 26 preludes and 26 fugues, one in each 13edo key.