385/384: Difference between revisions
No edit summary |
Cmloegcmluin (talk | contribs) expand upon known history of name |
||
| Line 4: | Line 4: | ||
| Monzo = -7 -1 1 1 1 | | Monzo = -7 -1 1 1 1 | ||
| Cents = 4.50256 | | Cents = 4.50256 | ||
| Name = | | Name = keenanisma,<br>undecimal kleisma | ||
| Color name = | | Color name = | ||
| FJS name = P1<sup>5, 7, 11</sup> | | FJS name = P1<sup>5, 7, 11</sup> | ||
| Line 10: | Line 10: | ||
}} | }} | ||
The ''' | The '''keenanisma''' or '''undecimal kleisma''' is the [[11-limit]] [[comma]] '''385/384''' = {{Monzo| -7 -1 1 1 1 }} of 4.503 [[cent]]s. It is both the interval that separates [[77/64]] and [[6/5]], and, the sum of the [[schisma]] and the [[symbiotic comma]]. Tempering it out leads to a temperament of the 11-limit rank four [[Keenanismic family]]. | ||
In addition to equating [[77/64]] and [[6/5]], tempering out the keenanisma equates [[48/35]] with [[11/8]], [[35/24]] with [[16/11]], and [[12/11]] with [[35/32]], which are [[7-limit]] intervals of low complexity, lying across from 1/1 in the hexanies 8/7-6/5-48/35-8/5-12/7-2 and 7/6-5/4-35/24-5/3-7/4-2. Hence keenanismic tempering allows the hexany to be viewed as containing some 11-limit harmony. The hexany is a fundamental construct in the 3D lattice of [[The_Seven_Limit_Symmetrical_Lattices|7-limit pitch classes]], the "deep holes" of the lattice as opposed to the "holes" represented by major and minor tetrads, and in terms of the [[The Seven Limit Symmetrical Lattices|cubic lattice of 7-limit tetrads]], the otonal tetrad with root 11 (or 11/8) is represented by [-2 0 0]: 1-6/5-48/35-12/7-2. In terms of 7-limit chord relationships, this complexity is as low as possible for an 11-limit projection comma, equaling the [0 1 -1] of 56/55 and less than the other alternatives. Since keenanismic temperament is also quite accurate, this singles it out as being of special interest. | In addition to equating [[77/64]] and [[6/5]], tempering out the keenanisma equates [[48/35]] with [[11/8]], [[35/24]] with [[16/11]], and [[12/11]] with [[35/32]], which are [[7-limit]] intervals of low complexity, lying across from 1/1 in the hexanies 8/7-6/5-48/35-8/5-12/7-2 and 7/6-5/4-35/24-5/3-7/4-2. Hence keenanismic tempering allows the hexany to be viewed as containing some 11-limit harmony. The hexany is a fundamental construct in the 3D lattice of [[The_Seven_Limit_Symmetrical_Lattices|7-limit pitch classes]], the "deep holes" of the lattice as opposed to the "holes" represented by major and minor tetrads, and in terms of the [[The Seven Limit Symmetrical Lattices|cubic lattice of 7-limit tetrads]], the otonal tetrad with root 11 (or 11/8) is represented by [-2 0 0]: 1-6/5-48/35-12/7-2. In terms of 7-limit chord relationships, this complexity is as low as possible for an 11-limit projection comma, equaling the [0 1 -1] of 56/55 and less than the other alternatives. Since keenanismic temperament is also quite accurate, this singles it out as being of special interest. | ||
| Line 19: | Line 19: | ||
[[File:keenanismic tetrads in 31edo sym.png|thumb]] | [[File:keenanismic tetrads in 31edo sym.png|thumb]] | ||
== Name == | |||
Originally this comma was recommended by Paul Erlich to be named "Keenan's kleisma", after Dave Keenan, due to "it figur[ing] particularly heavily in his many postings about microtemperament"<ref>https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_1161.html#1284</ref>. Dave himself initially resisted this eponymous naming, recommending a more descriptive name<ref> https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_7286.html#7286</ref>. And so undecimal kleisma was adopted<ref>https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_7286.html#7296</ref>, and to this day, undecimal kleisma in the Stichting Huygens-Fokker records<ref>https://www.huygens-fokker.org/docs/intervals.html</ref>. | |||
The history of the name "keenanisma" is less clear. It's possible that "Keenan's kleisma" remained in use, and eventually was altered to "keenanisma" following a pattern used for many commas named for people. Another possibility is that when a temperament based on this comma was being named, "undecimal kleisma" was seen as unfit to base the name upon, and so Keenan's name was referenced instead, leading to "keenanismic", and then later "keenanisma" was formed from that. | |||
== See also == | == See also == | ||
Revision as of 16:23, 15 January 2022
| Interval information |
undecimal kleisma
reduced
The keenanisma or undecimal kleisma is the 11-limit comma 385/384 = [-7 -1 1 1 1⟩ of 4.503 cents. It is both the interval that separates 77/64 and 6/5, and, the sum of the schisma and the symbiotic comma. Tempering it out leads to a temperament of the 11-limit rank four Keenanismic family.
In addition to equating 77/64 and 6/5, tempering out the keenanisma equates 48/35 with 11/8, 35/24 with 16/11, and 12/11 with 35/32, which are 7-limit intervals of low complexity, lying across from 1/1 in the hexanies 8/7-6/5-48/35-8/5-12/7-2 and 7/6-5/4-35/24-5/3-7/4-2. Hence keenanismic tempering allows the hexany to be viewed as containing some 11-limit harmony. The hexany is a fundamental construct in the 3D lattice of 7-limit pitch classes, the "deep holes" of the lattice as opposed to the "holes" represented by major and minor tetrads, and in terms of the cubic lattice of 7-limit tetrads, the otonal tetrad with root 11 (or 11/8) is represented by [-2 0 0]: 1-6/5-48/35-12/7-2. In terms of 7-limit chord relationships, this complexity is as low as possible for an 11-limit projection comma, equaling the [0 1 -1] of 56/55 and less than the other alternatives. Since keenanismic temperament is also quite accurate, this singles it out as being of special interest.
EDOs with patent vals tempering out the keenansima include 15, 19, 22, 31, 34, 37, 41, 53, 68, 72, 118, 159, 190, 212 and 284.
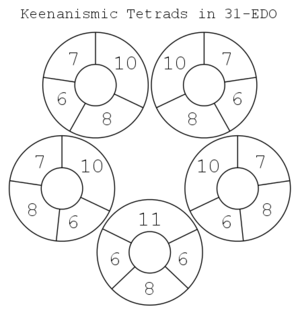
Characteristic of keenanismic tempering are the keenanismic tetrads, 385/384-tempered versions of 1-5/4-3/2-12/7, 1-5/4-10/7-12/7, 1-6/5-3/2-7/4, 1-5/4-16/11-7/4, and 1-14/11-16/11-7/4. These are essentially tempered dyadic chords, where every dyad of the chord is a keenanismic tempered version of an interval of the 11-odd-limit tonality diamond, and hence regarded as an 11-odd-limit consonance.
Name
Originally this comma was recommended by Paul Erlich to be named "Keenan's kleisma", after Dave Keenan, due to "it figur[ing] particularly heavily in his many postings about microtemperament"[1]. Dave himself initially resisted this eponymous naming, recommending a more descriptive name[2]. And so undecimal kleisma was adopted[3], and to this day, undecimal kleisma in the Stichting Huygens-Fokker records[4].
The history of the name "keenanisma" is less clear. It's possible that "Keenan's kleisma" remained in use, and eventually was altered to "keenanisma" following a pattern used for many commas named for people. Another possibility is that when a temperament based on this comma was being named, "undecimal kleisma" was seen as unfit to base the name upon, and so Keenan's name was referenced instead, leading to "keenanismic", and then later "keenanisma" was formed from that.
See also
- Keenanismic chords
- Keenanismic family, the rank-4 temperament family where it is tempered out
- Keenanismic temperaments, a collection of rank-3 temperaments where it is tempered out
- Small comma
- List of superparticular intervals
References
- ↑ https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_1161.html#1284
- ↑ https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_7286.html#7286
- ↑ https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_7286.html#7296
- ↑ https://www.huygens-fokker.org/docs/intervals.html