11-limit: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older editNewer edit →
VisualWikitext
Morion (talk | contribs)
14 edits
→Intervals 1: Corrected information as it was previously referring to 11-odd-limit.
Cleanup
Line 1: Line 1:
The '''11-limit''' consists of all [[Just intonation|justly tuned]] intervals whose numerators and denominators are both products of the primes 2, 3, 5, 7 and 11. Some examples of 11-limit intervals are [[14/11]], [[11/8]], [[27/22]] and [[99/98]]. The 11 odd-limit consists of intervals whose numerators and denominators, when all factors of two have been removed, are less than or equal to 11. Reduced to an octave, these are the ratios 1/1, 12/11, 11/10, 10/9, 9/8, 8/7, 7/6, 6/5, 11/9, 5/4, 14/11, 9/7, 4/3, 11/8, 7/5, 10/7, 16/11, 3/2, 14/9, 11/7, 8/5, 18/11, 5/3, 12/7, 7/4, 16/9, 9/5, 20/11, 11/6, 2/1. In an 11-limit system, all the ratios of the 11 odd-limit can be treated as potential consonances.
The '''11-limit''' consists of all [[Just intonation|justly tuned]] intervals whose numerators and denominators are both products of the primes 2, 3, 5, 7 and 11. Some examples of 11-limit intervals are [[14/11]], [[11/8]], [[27/22]] and [[99/98]]. The [[11-odd-limit]] consists of intervals whose numerators and denominators, when all factors of two have been removed, are less than or equal to 11. Reduced to an octave, these are the ratios 1/1, 12/11, 11/10, 10/9, 9/8, 8/7, 7/6, 6/5, 11/9, 5/4, 14/11, 9/7, 4/3, 11/8, 7/5, 10/7, 16/11, 3/2, 14/9, 11/7, 8/5, 18/11, 5/3, 12/7, 7/4, 16/9, 9/5, 20/11, 11/6, 2/1. In an 11-limit system, all the ratios of the 11 odd-limit can be treated as potential consonances.


== Intervals 1 ==
While the [[7-limit]] introduces subminor and supermajor intervals, which can sound like dramatic inflections of the familiar interval categories of [[12edo]], the 11-limit introduces neutral intervals, [[superfourth]]s and [[subfifth]]s, which fall in between major, minor and perfect [[interval category|interval categories]] and thus demand new distinctions. It is thus inescapably xenharmonic.
 
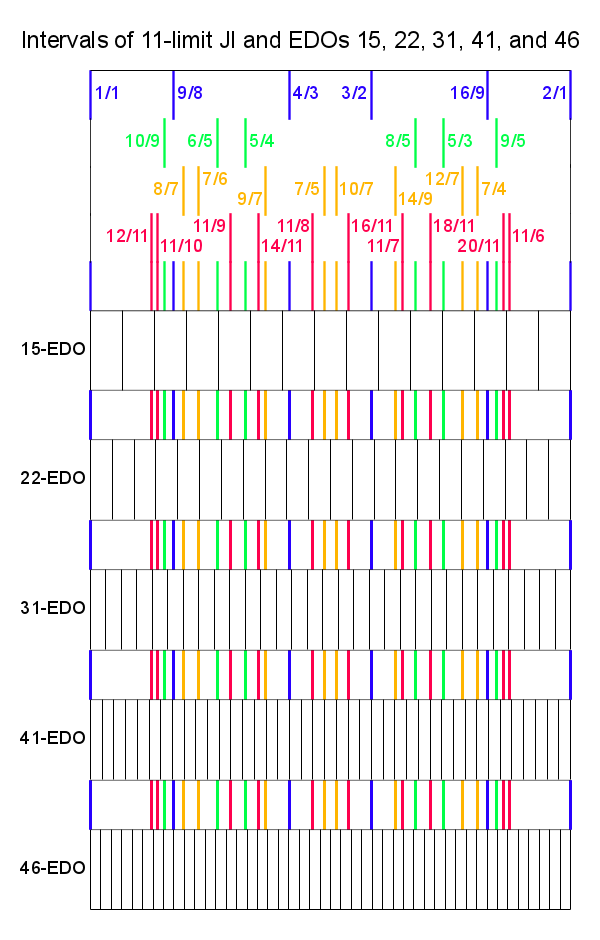
Examples of [[EDO]]s which represent 11-limit intervals well include: {{EDOs|22, 26, 31, 41, 46, 63, 72, 87, 109, 118, 152, and 161edo }}.


== Intervals ==
=== 11-odd-limit intervals ===
{| class="wikitable center-all"
{| class="wikitable center-all"
! Ratio
! Ratio
Line 153: Line 157:
| do-do
| do-do
|}
|}
While the [[7-limit]] introduces subminor and supermajor intervals, which can sound like dramatic inflections of the familiar interval categories of [[12edo]], the 11-limit introduces neutral intervals, [[superfourth]]s and [[subfifth]]s, which fall in between major, minor and perfect [[interval category|interval categories]] and thus demand new distinctions. It is thus inescapably xenharmonic.
Examples of [[EDO]]s which represent 11-limit intervals well include: {{EDOs|22, 26, 31, 41, 46, 63, 72, 87, 109, 118, 152, and 161edo }}.


[[File:11-limit_compare.png|alt=11-limit_compare.png|11-limit_compare.png]]
[[File:11-limit_compare.png|alt=11-limit_compare.png|11-limit_compare.png]]


==Intervals 2==
=== Selected 15-odd-limit intervals ===
 
Here are all the 15-odd-limit intervals of 11:
Here are all the 15-odd-limit intervals of 11:


Line 230: Line 229:
|}
|}


==Music==
== Music ==
* [http://sonic-arts.org/hill/10-passages-ji/10-passages-ji.htm Study #3] [http://sonic-arts.org/hill/10-passages-ji/04_hill_study-3.mp3 play] by [[Dave Hill]]
* [http://sonic-arts.org/hill/10-passages-ji/10-passages-ji.htm Brief 11-ratio composition] [http://sonic-arts.org/hill/10-passages-ji/09_hill_brief-11-ratio-composition.mp3 play] by Dave Hill
* [http://micro.soonlabel.com/just/11-limit/20120210-piano-11-limit.mp3 11 Limit Piano] by [[Chris Vaisvil]]
* [https://soundcloud.com/andrew_heathwaite/11-limit-singtervals 11-limit singtervals] by [[Andrew Heathwaite]]


*[http://sonic-arts.org/hill/10-passages-ji/10-passages-ji.htm Study #3] [http://sonic-arts.org/hill/10-passages-ji/04_hill_study-3.mp3 play] by [[Dave Hill]]
== See also ==
*[http://sonic-arts.org/hill/10-passages-ji/10-passages-ji.htm Brief 11-ratio composition] [http://sonic-arts.org/hill/10-passages-ji/09_hill_brief-11-ratio-composition.mp3 play] by Dave Hill
* [[Gallery of just intervals]]
*[http://micro.soonlabel.com/just/11-limit/20120210-piano-11-limit.mp3 11 Limit Piano] by [[Chris Vaisvil]]
* [[Harmonic limit]]
*[https://soundcloud.com/andrew_heathwaite/11-limit-singtervals 11-limit singtervals] by [[Andrew Heathwaite]]
* [[11-odd-limit]]
 
==See also==
 
*[[Gallery of just intervals]]
*[[Harmonic limit]]
*[[11-odd-limit]]


[[Category:Just intonation]]
[[Category:11-limit]]
[[Category:11-limit]]
[[Category:example]]
[[Category:Interval]]
[[Category:interval]]
[[Category:Limit]]
[[Category:limit]]
[[Category:Listen]]
[[Category:listen]]
[[Category:Prime limit]]
[[Category:prime_limit]]
 
[[Category:Todo]]

Revision as of 10:36, 24 October 2021

The 11-limit consists of all justly tuned intervals whose numerators and denominators are both products of the primes 2, 3, 5, 7 and 11. Some examples of 11-limit intervals are 14/11, 11/8, 27/22 and 99/98. The 11-odd-limit consists of intervals whose numerators and denominators, when all factors of two have been removed, are less than or equal to 11. Reduced to an octave, these are the ratios 1/1, 12/11, 11/10, 10/9, 9/8, 8/7, 7/6, 6/5, 11/9, 5/4, 14/11, 9/7, 4/3, 11/8, 7/5, 10/7, 16/11, 3/2, 14/9, 11/7, 8/5, 18/11, 5/3, 12/7, 7/4, 16/9, 9/5, 20/11, 11/6, 2/1. In an 11-limit system, all the ratios of the 11 odd-limit can be treated as potential consonances.

While the 7-limit introduces subminor and supermajor intervals, which can sound like dramatic inflections of the familiar interval categories of 12edo, the 11-limit introduces neutral intervals, superfourths and subfifths, which fall in between major, minor and perfect interval categories and thus demand new distinctions. It is thus inescapably xenharmonic.

Examples of EDOs which represent 11-limit intervals well include: 22, 26, 31, 41, 46, 63, 72, 87, 109, 118, 152, and 161edo.

Intervals

11-odd-limit intervals

Ratio Color name harmonic solfege
12/11 1u2 lu 2nd fu-sol
11/10 1og2 logu 2nd mi-fu
10/9 y2 yo 2nd re-mi
9/8 w2 wa 2nd do-re
8/7 r2 ru 2nd ta-do
7/6 z3 zo 3rd sol-ta
6/5 g3 gu 3rd mi-sol, ti-re
11/9 1o3 ilo 3rd re-fu
5/4 y3 yo 3rd do-mi
14/11 1uz4 luzo 4th fu-ta
9/7 r3 ru 3rd ta-re
4/3 w4 wa 4th do-fa
11/8 1o4 ilo 4th do-fu
7/5 zg5 zogu 5th mi-ta
10/7 ry4 ruyo 4th ta-mi
16/11 1u5 lu 5th fu-do
3/2 w5 wa 5th do-sol
14/9 z6 zo 6th re-ta
11/7 1or5 loru 5th ta-fu
8/5 g6 gu 6th mi-do
18/11 1u6 lu 6th fu-re
5/3 y6 yo 6th sol-mi
12/7 r6 ru 6th ta-sol
7/4 z7 zo 7th do-ta
16/9 w7 wa 7th re-do
9/5 g7 gu 7th mi-re
20/11 1uy7 luyo 7th fu-mi
11/6 1o7 ilo 7th sol-fu
2/1 w8 wa 8ve do-do

11-limit_compare.png

Selected 15-odd-limit intervals

Here are all the 15-odd-limit intervals of 11:

Ratio Site (¢) Color name
12/11 150.637 1u2 lu 2nd
11/10 165.004 1og2 logu 2nd
11/9 347.408 1o3 ilo 3rd
14/11 417.508 1uz4 lu 4th
15/11 536.951 1uy4 luyo 4th
11/8 551.318 1o4 ilo 4th
16/11 648.682 1u5 lu 5th
22/15 663.049 1og5 logu 5th
11/7 782.492 1or5 loru 5th
18/11 852.592 1u6 lu 6th
20/11 1034.996 1uy7 luyo 7th
11/6 1049.363 1o7 ilo 7th

Music

See also

Retrieved from "https://en.xen.wiki/index.php?title=11-limit&oldid=79866"