50edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
ArrowHead294 (talk | contribs)
14,512 edits
Sintel (talk | contribs)
autopatrolled
1,547 edits
→Approximation to JI: -zeta peak index
 
(37 intermediate revisions by 10 users not shown)
Line 1: Line 1:
{{Infobox ET}}
{{Infobox ET}}
{{ED intro}}


{{EDO intro|50}}
== Theory ==
== Theory ==
In the [[5-limit]], 50edo tempers out [[81/80]], making it a [[meantone]] system, and in that capacity has historically drawn some notice. In [http://lit.gfax.ch/Harmonics%202nd%20Edition%20%28Robert%20Smith%29.pdf "Harmonics or the Philosophy of Musical Sounds"] (1759) by Robert Smith, a musical temperament is described where the octave is divided into 50 equal parts – 50edo, in one word. Later, W.S.B. Woolhouse noted it was fairly close to the [[Target_tunings|least squares]] tuning for 5-limit meantone. 50edo, however, is especially interesting from a higher limit point of view. While [[31edo]] extends meantone with a [[7/4]] which is nearly pure, 50 has a flat 7/4 but both [[11/8]] and [[13/8]] are nearly pure. It is also the highest edo where the mapping of [[9/8]] and [[10/9]] to the same interval is [[consistent]], with two stacked fifths falling almost exactly 3/7 syntonic comma sharp of 10/9 and 4/7 comma flat of 9/8. It also maps all [[15-odd-limit]] intervals consistently, with the sole exceptions of 11/9 and 18/11.
As an equal temperament, 50et [[tempering out|tempers out]] [[81/80]] in the [[5-limit]], making it a [[meantone]] system, and in that capacity has historically drawn some notice; it is a somewhat sharp approximation of [[2/7-comma meantone]] (and is almost exactly 5/18-comma meantone). In [http://lit.gfax.ch/Harmonics%202nd%20Edition%20%28Robert%20Smith%29.pdf "Harmonics or the Philosophy of Musical Sounds"] (1759) by Robert Smith, a musical temperament is described where the octave is divided into 50 equal parts – 50edo, in one word. Later, {{w|W. S. B. Woolhouse}} noted it was fairly close to the [[Target_tunings|least squares]] tuning for 5-limit meantone. 50edo, however, is especially interesting from a higher-limit point of view. While [[31edo]] extends meantone with a [[7/4]] which is nearly pure, 50 has a flat 7/4 but both [[11/8]] and [[13/8]] are nearly pure. It is also the highest edo where the mapping of [[9/8]] and [[10/9]] to the same interval is [[consistent]], with two stacked fifths falling almost exactly 3/7-syntonic-comma sharp of 10/9 and 4/7-comma flat of 9/8. It also maps all [[15-odd-limit]] intervals consistently, with the sole exceptions of 11/9 and 18/11.


50edo tempers out [[126/125]], [[225/224]] and [[3136/3125]] in the [[7-limit]], indicating it [[support]]s septimal meantone; [[245/242]], [[385/384]] and [[540/539]] in the [[11-limit]] and [[105/104]], [[144/143]] and 196/195 in the [[13-limit]], and can be used for even higher limits. Aside from meantone and its extension meanpop, it can be used to advantage for the [[Starling temperaments #Coblack temperament|coblack (15&50) temperament]], and provides the optimal patent val for 11 and 13-limit [[Meantone_family #Bimeantone|bimeantone]]. It is also the unique equal temperament tempering out both 81/80 and the [[vishnuzma]], {{monzo|23 6 -14}}, so that in 50edo seven chromatic semitones stack to a perfect fourth. By comparison, this gives a perfect fifth in 12edo, a doubly diminished fifth in 31edo, and a diminished fourth in 19edo.
It tempers out [[126/125]], [[225/224]] and [[3136/3125]] in the [[7-limit]], indicating it [[support]]s septimal meantone; [[245/242]], [[385/384]] and [[540/539]] in the [[11-limit]] and [[105/104]], [[144/143]] and 196/195 in the [[13-limit]], and can be used for even higher limits. Aside from meantone and its extension [[meanpop]], it can be used to advantage for the [[coblack]] temperament (15 & 50), and provides the optimal patent val for 11- and 13-limit [[Meantone family #Bimeantone|bimeantone]]. It is also the unique equal temperament tempering out both 81/80 and the [[vishnuzma]], {{monzo| 23 6 -14 }}, so that in 50edo seven chromatic semitones stack to a perfect fourth. By comparison, this gives a perfect fifth in 12edo, a doubly diminished fifth in 31edo, and a diminished fourth in 19edo.


=== Odd harmonics ===
=== Odd harmonics ===
{{Harmonics in equal|50}}
{{Harmonics in equal|50|columns=15}}


=== Relations ===
=== Relations ===
Line 16: Line 16:
{| class="wikitable center-all right-2 left-3"
{| class="wikitable center-all right-2 left-3"
|-
|-
! #
! #
! Cents
! Cents
! Ratios*
! Ratios<ref group="note">{{sg|13-limit}}</ref>
! colspan="3" | [[Ups and Downs Notation]]
! colspan="3" | [[Ups and downs notation]]
([[Enharmonic unisons in ups and downs notation|EUs]]: v<sup>3</sup>A1 and vvd2)
|-
|-
| 0
| 0
Line 378: Line 379:
| D
| D
|}
|}
<nowiki>*</nowiki> using the patent val


== JI approximation ==
== Notation ==
=== Ups and downs notation ===
Spoken as up, downsharp, sharp, upsharp, etc. Note that downsharp can be respelled as dup (double-up), and upflat as dud.
{{sharpness-sharp3a}}
 
Using [[Helmholtz–Ellis]] accidentals, 50edo can also be notated using [[Alternative symbols for ups and downs notation#Sharp-3|alternative ups and downs]]:
{{Sharpness-sharp3}}
Here, a sharp raises by three steps, and a flat lowers by three steps, so arrows can be used to fill in the gap. If the arrows are taken to have their own layer of enharmonic spellings, some notes may be best spelled with double arrows.
 
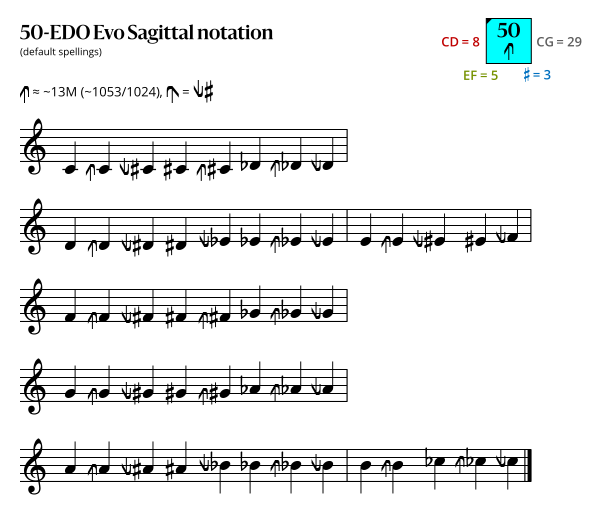
=== Sagittal notation ===
This notation uses the same sagittal sequence as EDOs [[57edo#Sagittal notation|57]], [[64edo#Sagittal notation|64]], and [[71edo#Second-best fifth notation|71b]].
 
==== Evo flavor ====
<imagemap>
File:50-EDO_Evo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 599 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 160 106 [[1053/1024]]
default [[File:50-EDO_Evo_Sagittal.svg]]
</imagemap>
 
==== Revo flavor ====
<imagemap>
File:50-EDO_Revo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 583 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 160 106 [[1053/1024]]
default [[File:50-EDO_Revo_Sagittal.svg]]
</imagemap>
 
In the diagrams above, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's [[Sagittal notation#Primary comma|primary comma]] (the comma it ''exactly'' represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it ''approximately'' represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this EDO.
 
== Approximation to JI ==
[[File:50ed2.svg|250px|thumb|right|alt=alt : Your browser has no SVG support.|Selected 29-limit intervals approximated in 50edo]]
[[File:50ed2.svg|250px|thumb|right|alt=alt : Your browser has no SVG support.|Selected 29-limit intervals approximated in 50edo]]
=== 15-odd-limit mappings ===
 
{{Q-odd-limit intervals|50}}
=== 15-odd-limit interval mappings ===
{{Q-odd-limit intervals|50|15}}


== Regular temperament properties ==
== Regular temperament properties ==
=== Temperament measures ===
=== Temperament measures ===
{| class="wikitable center-4 center-5 center-6"
{| class="wikitable center-4 center-5 center-6"
! rowspan="2" | Subgroup
|-
! rowspan="2" | [[Subgroup]]
! rowspan="2" | [[Comma list]]
! rowspan="2" | [[Comma list]]
! rowspan="2" | [[Mapping]]
! rowspan="2" | [[Mapping]]
Line 399: Line 435:
| 2.3
| 2.3
| {{monzo| -79 50 }}
| {{monzo| -79 50 }}
| [{{val| 50 79 }}]
| {{mapping| 50 79 }}
| +1.88
| +1.88
| 1.88
| 1.88
Line 405: Line 441:
|-
|-
| 2.3.5
| 2.3.5
| 81/80, 1220703125/1207959552
| 81/80, {{monzo| -27 -2 13 }}
| [{{val| 50 79 116 }}]
| {{mapping| 50 79 116 }}
| +1.58
| +1.58
| 1.59
| 1.59
Line 413: Line 449:
| 2.3.5.7
| 2.3.5.7
| 81/80, 126/125, 84035/82944
| 81/80, 126/125, 84035/82944
| [{{val| 50 79 116 140 }}]
| {{mapping| 50 79 116 140 }}
| +1.98
| +1.98
| 1.54
| 1.54
Line 420: Line 456:
| 2.3.5.7.11
| 2.3.5.7.11
| 81/80, 126/125, 245/242, 385/384
| 81/80, 126/125, 245/242, 385/384
| [{{val| 50 79 116 140 173 }}]
| {{mapping| 50 79 116 140 173 }}
| +1.54
| +1.54
| 1.63
| 1.63
Line 427: Line 463:
| 2.3.5.7.11.13
| 2.3.5.7.11.13
| 81/80, 105/104, 126/125, 144/143, 245/242
| 81/80, 105/104, 126/125, 144/143, 245/242
| [{{val| 50 79 116 140 173 185 }}]
| {{mapping| 50 79 116 140 173 185 }}
| +1.31
| +1.31
| 1.57
| 1.57
Line 434: Line 470:


=== Commas ===
=== Commas ===
50edo [[tempers out]] the following [[comma]]s. (Note: This assumes the [[val]] {{val|50 79 116 140 173 185 204 212 226}}, comma values in cents rounded to 2 decimal places.) This list is not all-inclusive, and is based on the interval table from Scala version 2.2.
50et [[tempering out|tempers out]] the following [[comma]]s. This assumes the [[val]] {{val| 50 79 116 140 173 185 204 212 226 }}, comma values in cents rounded to 2 decimal places. This list is not all-inclusive, and is based on the interval table from Scala version 2.2.


{| class="commatable wikitable center-all left-3 right-4 left-5"
{| class="commatable wikitable center-all left-3 right-4 left-5"
|-
|-
! [[Harmonic limit|Prime<br>Limit]]
! [[Harmonic limit|Prime<br>limit]]
! [[Ratio]]<ref>Ratios longer than 10 digits are presented by placeholders with informative hints</ref>
! [[Ratio]]<ref group="note">{{rd}}</ref>
! [[Monzo]]
! [[Monzo]]
! [[Cent]]s
! [[Cent]]s
Line 502: Line 538:
| {{monzo| 6 0 -5 2 }}
| {{monzo| 6 0 -5 2 }}
| 6.08
| 6.08
| Hemimean
| Hemimean comma
|-
|-
| 7
| 7
Line 508: Line 544:
| {{monzo| 11 -10 -10 10 }}
| {{monzo| 11 -10 -10 10 }}
| 5.57
| 5.57
| [[Linus]]
| [[Linus comma]]
|-
|-
| 7
| 7
Line 526: Line 562:
| {{monzo| -1 0 1 2 -2 }}
| {{monzo| -1 0 1 2 -2 }}
| 21.33
| 21.33
| Cassacot
| Frostma
|-
|-
| 11
| 11
Line 544: Line 580:
| {{monzo| 5 -1 3 0 -3 }}
| {{monzo| 5 -1 3 0 -3 }}
| 3.03
| 3.03
| Wizardharry
| Wizardharry comma
|-
|-
| 11
| 11
Line 574: Line 610:
| {{monzo| 2 3 0 -1 1 -2 }}
| {{monzo| 2 3 0 -1 1 -2 }}
| 7.30
| 7.30
| Kestrel Comma
| Kestrel comma
|-
|-
| 13
| 13
Line 586: Line 622:
| {{monzo| 2 -1 0 1 -2 1 }}
| {{monzo| 2 -1 0 1 -2 1 }}
| 4.76
| 4.76
| Gentle comma
| Minor minthma
|-
|-
| 13
| 13
Line 610: Line 646:
| {{monzo| -5 -2 0 0 0 0 2 }}
| {{monzo| -5 -2 0 0 0 0 2 }}
| 6.00
| 6.00
| Septendecimal semitones comma
| Semitonisma
|-
|-
| 17
| 17
Line 678: Line 714:
| Triaphonisma
| Triaphonisma
|}
|}
<references/>


=== Rank-2 temperaments ===
=== Rank-2 temperaments ===
{| class="wikitable center-all left-5"
{| class="wikitable center-all left-5"
|+ Table of rank-2 temperaments by generator
|+ style="font-size: 105%;" | Table of rank-2 temperaments by generator
|-
|-
! Periods<br> per Octave
! Periods<br>per 8ve
! Generator
! Generator*
! Cents
! Cents*
! Associated<br>Ratio
! Associated<br>ratio*
! Temperament
! Temperament
|-
|-
| 1
| 1
| 1\50
| 1\50
| 24.00
| 24.0
| 686/675
| 686/675
| [[Sengagen]]
| [[Sengagen]]
Line 698: Line 733:
| 1
| 1
| 9\50
| 9\50
| 216.00
| 216.0
| 17/15
| 17/15
| [[Tremka]]
| [[Tremka]]
Line 704: Line 739:
| 1
| 1
| 11\50
| 11\50
| 264.00
| 264.0
| 7/6
| 7/6
| [[Septimin]]
| [[Septimin]]
Line 710: Line 745:
| 1
| 1
| 13\50
| 13\50
| 312.00
| 312.0
| 6/5
| 6/5
| [[Oolong]]
| [[Oolong]]
Line 716: Line 751:
| 1
| 1
| 17\50
| 17\50
| 408.00
| 408.0
| 15625/12288
| 325/256
| [[Ditonic]] / [[coditone]]
| [[Coditone]]
|-
|-
| 1
| 1
| 19\50
| 19\50
| 456.00
| 456.0
| 125/96
| 125/96
| [[Qak]]
| [[Qak]]
Line 728: Line 763:
| 1
| 1
| 21\50
| 21\50
| 504.00
| 504.0
| 4/3
| 4/3
| [[Meantone]] / [[meanpop]]
| [[Meantone]] / [[meanpop]]
Line 734: Line 769:
| 1
| 1
| 23\50
| 23\50
| 552.00
| 552.0
| 11/8
| 11/8
| [[Emka]]
| [[Emka]]
Line 740: Line 775:
| 2
| 2
| 2\50
| 2\50
| 48.00
| 48.0
| 36/35
| 36/35
| [[Pombe]]
| [[Pombe]]
Line 746: Line 781:
| 2
| 2
| 3\50
| 3\50
| 72.00
| 72.0
| 25/24
| 25/24
| [[Vishnu]] / [[vishnean]]
| [[Vishnu]] / [[vishnean]]
|-
| 2
| 4\50
| 96.00
| 35/33
| [[Bimeantone]]
|-
|-
| 2
| 2
| 6\50
| 6\50
| 144.00
| 144.0
| 12/11
| 12/11
| [[Bisemidim]]
| [[Bisemidim]]
Line 764: Line 793:
| 2
| 2
| 9\50
| 9\50
| 216.00
| 216.0
| 17/15
| 17/15
| [[Wizard]] / [[lizard]] / [[gizzard]]
| [[Wizard]] / [[lizard]] / [[gizzard]]
Line 770: Line 799:
| 2
| 2
| 12\50
| 12\50
| 288.00
| 288.0
| 13/11
| 13/11
| [[Vines]]
| [[Vines]]
|-
| 2
| 21\50<br>(4\50)
| 504.0<br>(96.0)
| 4/3<br>(35/33)
| [[Bimeantone]]
|-
|-
| 5
| 5
| 21\50 <br>(1\50)
| 21\50<br>(1\50)
| 504.00 <br>(24.00)
| 504.0<br>(24.0)
| 4/3 <br>&nbsp;
| 4/3<br>(49/48)
| [[Cloudtone]]
| [[Cloudtone]]
|-
|-
| 5
| 5
| 3\50
| 23<br>(3\50)
| 72.00
| 552.0<br>(72.0)
| 21/20, 25/24
| 11/8<br>(21/20)
| [[Coblack]]
| [[Coblack]]
|-
|-
| 10
| 10
| 21\50 <br>(1\50)
| 7\50<br>(3\50)
| 504.00 <br>(24.00)
| 168.0<br>(72.0)
| 4/3 <br>&nbsp;
| 54/49<br>(25/24)
| [[Decic]]
| [[Decavish]]
|-
|-
| 10
| 10
| 2\50 <br>(3\50)
| 21\50<br>(1\50)
| 48.00 <br>(72.00)
| 504.0<br>(24.0)
| 36/35 <br>(25/24)
| 4/3<br>(78/77)
| [[Decavish]]
| [[Decic]]
|}
|}
<nowiki/>* [[Normal lists|Octave-reduced form]], reduced to the first half-octave, and [[Normal lists|minimal form]] in parentheses if distinct


== Instruments ==
== Instruments ==
'''Lumatone'''
; Lumatone


See [[Lumatone mapping for 50edo]]
See [[Lumatone mapping for 50edo]]
; Piano
A [[:Category:Piano|piano]] playing with a 50edo ensemble may wish to use the tuning [[116ed5]]. This tuning is almost exactly the same as 50edo, but with octaves [[octave stretch|stretched]] by 1 cent. Because pianos usually use stretched octaves, this tuning will sit better with the [[timbre]] of the piano, while still being close enough that it sounds perfectly in-tune with the other instruments tuned to 50edo.


== Music ==
== Music ==
=== Modern renderings ===
=== Modern renderings ===
; {{W|Johann Sebastian Bach}}
; {{W|Johann Sebastian Bach}}
* [https://www.youtube.com/watch?v=e6fMO-sue4Y "Contrapunctus 4" from ''The Art of Fugue'', BWV 1080] (1742–1749) – rendered by Claudi Meneghin (2024)
* [https://www.youtube.com/watch?v=RnYqc0NKMLM "Ricercar a 3" from ''The Musical Offering'', BWV 1079] (1747) – rendered by Claudi Meneghin (2024)
* [https://www.youtube.com/watch?v=M3wQu4UF1pg "Contrapunctus 11" from ''The Art of Fugue'', BWV 1080] (1742–1749) – rendered by Claudi Meneghin (2024)
* [https://www.youtube.com/watch?v=e6fMO-sue4Y "Contrapunctus 4" from ''The Art of Fugue'', BWV 1080] (1742–1749) &ndash; rendered by Claudi Meneghin (2024)
* [https://www.youtube.com/watch?v=M3wQu4UF1pg "Contrapunctus 11" from ''The Art of Fugue'', BWV 1080] (1742–1749) &ndash; rendered by Claudi Meneghin (2024, organ sound rendering)
* [https://www.youtube.com/watch?v=qjb9DDM32Ic "Contrapunctus 11" from ''The Art of Fugue'', BWV 1080] (1742-1749) &mdash; rendered by Claudi Meneghin (2025, harpsichord sound rendering)


; {{W|Nicolaus Bruhns}}
; {{W|Nicolaus Bruhns}}
* [https://www.youtube.com/watch?v=yrM50pvmD5c ''Prelude in E Minor "The Great"''] – rendered by Claudi Meneghin (2023)
* [https://www.youtube.com/watch?v=yrM50pvmD5c ''Prelude in E Minor "The Great"''] &ndash; rendered by Claudi Meneghin (2023)


; {{W|Gabriel Fauré}}
; {{W|Gabriel Fauré}}
* [https://www.youtube.com/watch?v=7djfrUlw2ck  ''Pavane'', op. 50] (1887) – arranged for harpsichord and rendered by Claudi Meneghin (2020)
* [https://www.youtube.com/watch?v=7djfrUlw2ck  ''Pavane'', op. 50] (1887) &ndash; arranged for harpsichord and rendered by Claudi Meneghin (2020)


; {{W|Akira Kamiya}}
; {{W|Akira Kamiya}}
* [https://www.youtube.com/watch?v=5UnPAhRqmb4 ''funfunfun ta yo''] (2007) – rendered by MortisTheneRd (2024)
* [https://www.youtube.com/watch?v=5UnPAhRqmb4 ''funfunfun ta yo''] (2007) &ndash; rendered by MortisTheneRd (2024)


=== 21st century===
=== 21st century===
; [[Bryan Deister]]
* [https://www.youtube.com/shorts/zCsc5n6dr_I ''microtonal improv in 50edo''] (2024)
* [https://www.youtube.com/shorts/ynz5XvJOHiE ''Piano that may not be played that well - Deltarune (microtonal cover in 50edo)''] (2025)
; [[Francium]]
; [[Francium]]
* [https://www.youtube.com/watch?v=pH6E35hwUnM ''On My Way To Somewhere''] (2023)
* [https://www.youtube.com/watch?v=pH6E35hwUnM ''On My Way To Somewhere''] (2023)


; [[Claudi Meneghin]]
; [[Claudi Meneghin]]
* [http://micro.soonlabel.com/gene_ward_smith/Others/Meneghin/Claudi-Meneghin-Twinkle-canon-50-edo.mp3 Twinkle canon – 50 edo] {{dead link}}
* [http://micro.soonlabel.com/gene_ward_smith/Others/Meneghin/Claudi-Meneghin-Twinkle-canon-50-edo.mp3 Twinkle canon &ndash; 50 edo] {{dead link}}
* [https://www.youtube.com/watch?v=wcTVED9zFrU ''Blue Fugue for Organ''] (2018)
* [https://www.youtube.com/watch?v=wcTVED9zFrU ''Blue Fugue for Organ''] (2018)
* [https://www.youtube.com/watch?v=Zh2jWoIXAf8 ''La Petite Poule Grise - Fugue''] (2019)
* [https://www.youtube.com/watch?v=Zh2jWoIXAf8 ''La Petite Poule Grise - Fugue''] (2019)
Line 850: Line 897:
* [http://www.music.ed.ac.uk/russell/conference/robertsmithkirckman.html More information about Robert Smith's temperament]{{Dead link}}
* [http://www.music.ed.ac.uk/russell/conference/robertsmithkirckman.html More information about Robert Smith's temperament]{{Dead link}}
* [https://www.dropbox.com/sh/4x81rzpkot32qzk/MQ3cJljjkh 50EDO Theory - Intervals, Chords and Scales in 50EDO by Cam Taylor]{{Dead link}}
* [https://www.dropbox.com/sh/4x81rzpkot32qzk/MQ3cJljjkh 50EDO Theory - Intervals, Chords and Scales in 50EDO by Cam Taylor]{{Dead link}}
* [http://iamcamtaylor.wordpress.com/ iamcamtaylor - Blog on 50EDO and extended meantone theory by Cam Taylor]    
* [http://iamcamtaylor.wordpress.com/ iamcamtaylor - Blog on 50EDO and extended meantone theory by Cam Taylor]    
 
== Notes ==
<references group="note" />


[[Category:50edo]]
[[Category:50edo]]
[[Category:Equal divisions of the octave|##]] <!-- 2-digit number -->
[[Category:Equal divisions of the octave|##]] <!-- 2-digit number -->
[[Category:Golden meantone]]
[[Category:Golden meantone]]
[[Category:Historical]]
[[Category:Listen]]
[[Category:Meantone]]
[[Category:Meantone]]
[[Category:Meanpop]]
[[Category:Meanpop]]
[[Category:Historical]]
[[Category:Listen]]

Latest revision as of 00:15, 16 August 2025

← 49edo 50edo 51edo →
Prime factorization 2 × 52
Step size 24 ¢ 
Fifth 29\50 (696 ¢)
Semitones (A1:m2) 3:5 (72 ¢ : 120 ¢)
Consistency limit 9
Distinct consistency limit 7

50 equal divisions of the octave (abbreviated 50edo or 50ed2), also called 50-tone equal temperament (50tet) or 50 equal temperament (50et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 50 equal parts of exactly 24 ¢ each. Each step represents a frequency ratio of 21/50, or the 50th root of 2.

Theory

As an equal temperament, 50et tempers out 81/80 in the 5-limit, making it a meantone system, and in that capacity has historically drawn some notice; it is a somewhat sharp approximation of 2/7-comma meantone (and is almost exactly 5/18-comma meantone). In "Harmonics or the Philosophy of Musical Sounds" (1759) by Robert Smith, a musical temperament is described where the octave is divided into 50 equal parts – 50edo, in one word. Later, W. S. B. Woolhouse noted it was fairly close to the least squares tuning for 5-limit meantone. 50edo, however, is especially interesting from a higher-limit point of view. While 31edo extends meantone with a 7/4 which is nearly pure, 50 has a flat 7/4 but both 11/8 and 13/8 are nearly pure. It is also the highest edo where the mapping of 9/8 and 10/9 to the same interval is consistent, with two stacked fifths falling almost exactly 3/7-syntonic-comma sharp of 10/9 and 4/7-comma flat of 9/8. It also maps all 15-odd-limit intervals consistently, with the sole exceptions of 11/9 and 18/11.

It tempers out 126/125, 225/224 and 3136/3125 in the 7-limit, indicating it supports septimal meantone; 245/242, 385/384 and 540/539 in the 11-limit and 105/104, 144/143 and 196/195 in the 13-limit, and can be used for even higher limits. Aside from meantone and its extension meanpop, it can be used to advantage for the coblack temperament (15 & 50), and provides the optimal patent val for 11- and 13-limit bimeantone. It is also the unique equal temperament tempering out both 81/80 and the vishnuzma, [23 6 -14⟩, so that in 50edo seven chromatic semitones stack to a perfect fourth. By comparison, this gives a perfect fifth in 12edo, a doubly diminished fifth in 31edo, and a diminished fourth in 19edo.

Odd harmonics

Approximation of odd harmonics in 50edo
Harmonic 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31
Error Absolute (¢) -6.0 -2.3 -8.8 -11.9 +0.7 -0.5 -8.3 -9.0 -9.5 +9.2 -4.3 -4.6 +6.1 +2.4 +7.0
Relative (%) -24.8 -9.6 -36.8 -49.6 +2.8 -2.2 -34.5 -37.3 -39.6 +38.4 -17.8 -19.3 +25.6 +10.1 +29.0
Steps
(reduced) 		79
(29) 		116
(16) 		140
(40) 		158
(8) 		173
(23) 		185
(35) 		195
(45) 		204
(4) 		212
(12) 		220
(20) 		226
(26) 		232
(32) 		238
(38) 		243
(43) 		248
(48)

Relations

The 50edo system is related to 7edo, 12edo, 19edo, 31edo as the next approximation to the "Golden Tone System" (Das Goldene Tonsystem) of Thorvald Kornerup (and similarly as the next step from 31edo in Joseph Yasser's "A Theory of Evolving Tonality").

Intervals

# Cents Ratios[note 1] Ups and downs notation

(EUs: v3A1 and vvd2)

0 0 1/1 Perfect 1sn P1 D
1 24 45/44, 49/48, 56/55, 65/64, 66/65, 78/77, 91/90, 99/98, 100/99, 121/120, 169/168 Up 1sn ^1 ^D
2 48 27/26, 33/32, 36/35, 50/49, 55/54, 64/63 Dim 2nd, Downaug 1sn d2, vA1 Ebb, vD#
3 72 21/20, 25/24, 26/25, 28/27 Aug 1sn, Updim 2nd A1, ^d2 D#, ^Ebb
4 96 22/21 Downminor 2nd vm2 vEb
5 120 16/15, 15/14, 14/13 Minor 2nd m2 Eb
6 144 13/12, 12/11 Upminor 2nd ^m2 ^Eb
7 168 11/10 Downmajor 2nd vM2 vE
8 192 9/8, 10/9 Major 2nd M2 E
9 216 25/22 Upmajor 2nd ^M2 ^E
10 240 8/7, 15/13 Downaug 2nd, Dim 3rd vA2, d3 vE#, Fb
11 264 7/6 Updim 3rd, Aug 2nd ^d3, A2 ^Fb, E#
12 288 13/11 Downminor 3rd vm3 vF
13 312 6/5 Minor 3rd m3 F
14 336 27/22, 39/32, 40/33, 49/40 Upminor 3rd ^m3 ^F
15 360 16/13, 11/9 Downmajor 3rd vM3 vF#
16 384 5/4 Major 3rd M3 F#
17 408 14/11 Upmajor 3rd ^M3 ^F#
18 432 9/7 Downaug 3rd, Dim 4th vA3, d4 vFx, Gb
19 456 13/10 Updim 4th, Aug 3rd A3, ^d4 ^Gb, Fx
20 480 33/25, 55/42, 64/49 Down 4th v4 vG
21 504 4/3 Perfect 4th P4 G
22 528 15/11 Up 4th ^4 ^G
23 552 11/8, 18/13 Downaug 4th vA4 vG#
24 576 7/5 Aug 4th A4 G#
25 600 63/44, 88/63, 78/55, 55/39 Upaug 4th, Downdim 5th ^A4, vd5 ^G#, vAb
26 624 10/7 Dim 5th d5 Ab
27 648 16/11, 13/9 Updim 5th ^d5 ^Ab
28 672 22/15 Down 5th v5 vA
29 696 3/2 Perfect 5th P5 A
30 720 50/33, 84/55, 49/32 Up 5th ^5 ^A
31 744 20/13 Downaug 5th, Dim 6th vA5, d6 vA#, Bbb
32 768 14/9 Updim 6th, Aug 5th ^d6, A5 ^Bbb, A#
33 792 11/7 Downminor 6th vm6 vBb
34 816 8/5 Minor 6th m6 Bb
35 840 13/8, 18/11 Upminor 6th ^m6 ^Bb
36 864 44/27, 64/39, 33/20, 80/49 Downmajor 6th vM6 vB
37 888 5/3 Major 6th M6 B
38 912 22/13 Upmajor 6th ^M6 ^B
39 936 12/7 Downaug 6th, Dim 7th vA6, d7 vB#, Cb
40 960 7/4 Updim 7th, Aug 6th ^d7, A6 ^Cb, B#
41 984 44/25 Downminor 7th vm7 vC
42 1008 16/9, 9/5 Minor 7th m7 C
43 1032 20/11 Upminor 7th ^m7 ^C
44 1056 24/13, 11/6 Downmajor 7th vM7 vC#
45 1080 15/8, 28/15, 13/7 Major 7th M7 C#
46 1104 21/11 Upmajor 7th ^M7 ^C#
47 1128 40/21, 48/25, 25/13, 27/14 Downaug 7th, Dim 8ve vA7, d8 vCx, Db
48 1152 52/27, 64/33, 35/18, 49/25, 108/55, 63/32 Updim 8ve, Aug 7th ^d8, A7 ^Db, Cx
49 1176 88/45, 96/49, 55/28, 128/65, 65/33, 77/39, 180/91, 196/99, 99/50, 240/121, 336/169 Down 8ve v8 vD
50 1200 2/1 Perfect 8ve P8 D

Notation

Ups and downs notation

Spoken as up, downsharp, sharp, upsharp, etc. Note that downsharp can be respelled as dup (double-up), and upflat as dud.

Step offset 0 1 2 3 4 5 6 7
Sharp symbol  
         
Flat symbol
           

Using Helmholtz–Ellis accidentals, 50edo can also be notated using alternative ups and downs:

Step offset 0 1 2 3 4 5 6 7
Sharp symbol  
 
 		 
 		 
 		 
 		 
 		 
Flat symbol  
 		 
 		 
 
 		 

Here, a sharp raises by three steps, and a flat lowers by three steps, so arrows can be used to fill in the gap. If the arrows are taken to have their own layer of enharmonic spellings, some notes may be best spelled with double arrows.

Sagittal notation

This notation uses the same sagittal sequence as EDOs 57, 64, and 71b.

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation1053/1024

Revo flavor

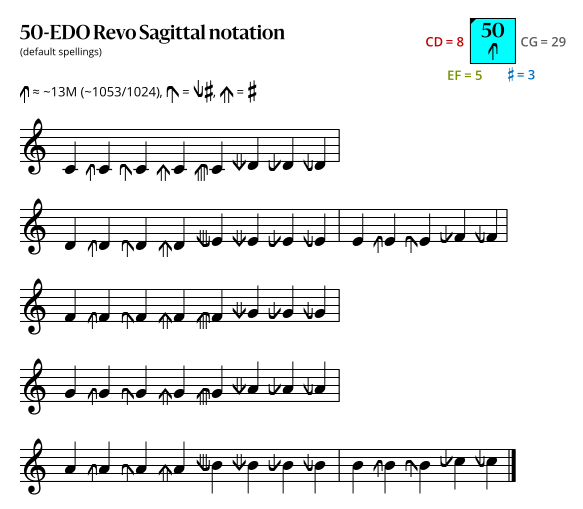
Sagittal notationPeriodic table of EDOs with sagittal notation1053/1024

In the diagrams above, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's primary comma (the comma it exactly represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it approximately represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this EDO.

Approximation to JI

alt : Your browser has no SVG support.
Selected 29-limit intervals approximated in 50edo

15-odd-limit interval mappings

The following tables show how 15-odd-limit intervals are represented in 50edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 50edo (direct approximation, even if inconsistent)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
13/8, 16/13 0.528 2.2
15/14, 28/15 0.557 2.3
11/8, 16/11 0.682 2.8
13/11, 22/13 1.210 5.0
13/10, 20/13 1.786 7.4
5/4, 8/5 2.314 9.6
7/6, 12/7 2.871 12.0
11/10, 20/11 2.996 12.5
9/7, 14/9 3.084 12.9
5/3, 6/5 3.641 15.2
13/12, 24/13 5.427 22.6
3/2, 4/3 5.955 24.8
7/5, 10/7 6.512 27.1
11/6, 12/11 6.637 27.7
15/13, 26/15 7.741 32.3
15/8, 16/15 8.269 34.5
13/7, 14/13 8.298 34.6
7/4, 8/7 8.826 36.8
15/11, 22/15 8.951 37.3
11/7, 14/11 9.508 39.6
9/5, 10/9 9.596 40.0
13/9, 18/13 11.382 47.4
11/9, 18/11 11.408 47.5
9/8, 16/9 11.910 49.6
15-odd-limit intervals in 50edo (patent val mapping)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
13/8, 16/13 0.528 2.2
15/14, 28/15 0.557 2.3
11/8, 16/11 0.682 2.8
13/11, 22/13 1.210 5.0
13/10, 20/13 1.786 7.4
5/4, 8/5 2.314 9.6
7/6, 12/7 2.871 12.0
11/10, 20/11 2.996 12.5
9/7, 14/9 3.084 12.9
5/3, 6/5 3.641 15.2
13/12, 24/13 5.427 22.6
3/2, 4/3 5.955 24.8
7/5, 10/7 6.512 27.1
11/6, 12/11 6.637 27.7
15/13, 26/15 7.741 32.3
15/8, 16/15 8.269 34.5
13/7, 14/13 8.298 34.6
7/4, 8/7 8.826 36.8
15/11, 22/15 8.951 37.3
11/7, 14/11 9.508 39.6
9/5, 10/9 9.596 40.0
13/9, 18/13 11.382 47.4
9/8, 16/9 11.910 49.6
11/9, 18/11 12.592 52.5

Regular temperament properties

Temperament measures

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3 [-79 50⟩ [⟨50 79]] +1.88 1.88 7.83
2.3.5 81/80, [-27 -2 13⟩ [⟨50 79 116]] +1.58 1.59 6.62
2.3.5.7 81/80, 126/125, 84035/82944 [⟨50 79 116 140]] +1.98 1.54 6.39
2.3.5.7.11 81/80, 126/125, 245/242, 385/384 [⟨50 79 116 140 173]] +1.54 1.63 6.76
2.3.5.7.11.13 81/80, 105/104, 126/125, 144/143, 245/242 [⟨50 79 116 140 173 185]] +1.31 1.57 6.54

Commas

50et tempers out the following commas. This assumes the val ⟨50 79 116 140 173 185 204 212 226], comma values in cents rounded to 2 decimal places. This list is not all-inclusive, and is based on the interval table from Scala version 2.2.

Prime
limit 		Ratio[note 2] Monzo Cents Name
3 (20 digits) [-79 50⟩ 297.75 50-comma
5 81/80 [-4 4 -1⟩ 21.51 Syntonic comma
5 (20 digits) [-27 -2 13⟩ 18.17 Ditonma
5 (20 digits) [23 6 -14⟩ 3.34 Vishnuzma
7 59049/57344 [-13 10 0 -1⟩ 50.72 Harrison's comma
7 16807/16384 [-14 0 0 5⟩ 44.13 Cloudy comma
7 3645/3584 [-9 6 1 -1⟩ 29.22 Schismean comma
7 126/125 [1 2 -3 1⟩ 13.79 Starling comma
7 225/224 [-5 2 2 -1⟩ 7.71 Marvel comma
7 3136/3125 [6 0 -5 2⟩ 6.08 Hemimean comma
7 (24 digits) [11 -10 -10 10⟩ 5.57 Linus comma
7 (12 digits) [-11 2 7 -3⟩ 1.63 Meter
7 (12 digits) [-6 -8 2 5⟩ 1.12 Wizma
11 245/242 [-1 0 1 2 -2⟩ 21.33 Frostma
11 385/384 [-7 -1 1 1 1⟩ 4.50 Keenanisma
11 540/539 [2 3 1 -2 -1⟩ 3.21 Swetisma
11 4000/3993 [5 -1 3 0 -3⟩ 3.03 Wizardharry comma
11 9801/9800 [-3 4 -2 -2 2⟩ 0.18 Kalisma
13 105/104 [-3 1 1 1 0 -1⟩ 16.57 Animist comma
13 144/143 [4 2 0 0 -1 -1⟩ 12.06 Grossma
13 196/195 [2 -1 -1 2 0 -1⟩ 8.86 Mynucuma
13 1188/1183 [2 3 0 -1 1 -2⟩ 7.30 Kestrel comma
13 31213/31104 [-7 -5 0 4 0 1⟩ 6.06 Praveensma
13 364/363 [2 -1 0 1 -2 1⟩ 4.76 Minor minthma
13 2200/2197 [3 0 2 0 1 -3⟩ 2.36 Petrma
17 170/169 [1 0 1 0 0 -2 1⟩ 10.21 Major naiadma
17 221/220 [-2 0 -1 0 -1 1 1⟩ 7.85 Minor naiadma
17 289/288 [-5 -2 0 0 0 0 2⟩ 6.00 Semitonisma
17 375/374 [-1 1 3 0 -1 0 -1⟩ 4.62 Ursulisma
19 153/152 [-3 2 0 0 0 0 1 -1⟩ 11.35 Ganassisma
19 171/170 [-1 2 -1 0 0 0 -1 1⟩ 10.15 Malcolmisma
19 210/209 [1 1 1 1 -1 0 0 1⟩ 8.26 Spleen comma
19 324/323 [2 4 0 0 0 0 -1 -1⟩ 5.35 Photisma
19 361/360 [-3 -2 -1 0 0 0 0 2⟩ 4.80 Go comma
19 495/494 [-1 2 1 0 1 -1 0 -1⟩ 3.50 Eulalisma
23 507/506 2.3.11.13.23 [-1 1 -1 2 -1⟩ 3.42 Laodicisma
23 529/528 2.3.11.23 [-4 -1 -1 2⟩ 3.28 Preziosisma
23 576/575 2.3.5.23 [6 2 -2 -1⟩ 3.01 Worcester comma
23 1288/1287 [3 -2 0 1 -1 -1 0 0 1⟩ 1.34 Triaphonisma

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods
per 8ve 		Generator* Cents* Associated
ratio* 		Temperament
1 1\50 24.0 686/675 Sengagen
1 9\50 216.0 17/15 Tremka
1 11\50 264.0 7/6 Septimin
1 13\50 312.0 6/5 Oolong
1 17\50 408.0 325/256 Coditone
1 19\50 456.0 125/96 Qak
1 21\50 504.0 4/3 Meantone / meanpop
1 23\50 552.0 11/8 Emka
2 2\50 48.0 36/35 Pombe
2 3\50 72.0 25/24 Vishnu / vishnean
2 6\50 144.0 12/11 Bisemidim
2 9\50 216.0 17/15 Wizard / lizard / gizzard
2 12\50 288.0 13/11 Vines
2 21\50
(4\50) 		504.0
(96.0) 		4/3
(35/33) 		Bimeantone
5 21\50
(1\50) 		504.0
(24.0) 		4/3
(49/48) 		Cloudtone
5 23
(3\50) 		552.0
(72.0) 		11/8
(21/20) 		Coblack
10 7\50
(3\50) 		168.0
(72.0) 		54/49
(25/24) 		Decavish
10 21\50
(1\50) 		504.0
(24.0) 		4/3
(78/77) 		Decic

* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct

Instruments

Lumatone

See Lumatone mapping for 50edo


Piano

A piano playing with a 50edo ensemble may wish to use the tuning 116ed5. This tuning is almost exactly the same as 50edo, but with octaves stretched by 1 cent. Because pianos usually use stretched octaves, this tuning will sit better with the timbre of the piano, while still being close enough that it sounds perfectly in-tune with the other instruments tuned to 50edo.

Music

Modern renderings

Johann Sebastian Bach
Nicolaus Bruhns
Gabriel Fauré
  • Pavane, op. 50 (1887) – arranged for harpsichord and rendered by Claudi Meneghin (2020)
Akira Kamiya

21st century

Bryan Deister
Francium
Claudi Meneghin
Cam Taylor

Additional reading

Notes

  1. ↑ Based on treating 13-limit as a 5-limit temperament; other approaches are also possible.
  2. ↑ Ratios longer than 10 digits are presented by placeholders with informative hints.
Retrieved from "https://en.xen.wiki/index.php?title=50edo&oldid=207071"