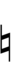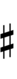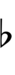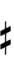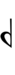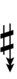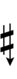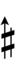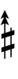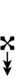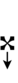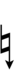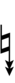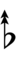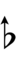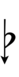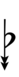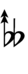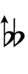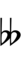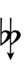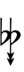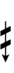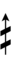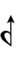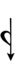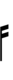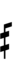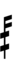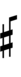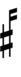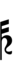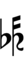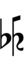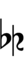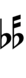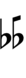65edo: Difference between revisions
Wikispaces>xenwolf **Imported revision 602901538 - Original comment: ** |
m →Music: fix formatting |
||
| (68 intermediate revisions by 24 users not shown) | |||
| Line 1: | Line 1: | ||
{{Infobox ET}} | |||
{{ED intro}} | |||
= | == Theory == | ||
65et can be characterized as the temperament which [[tempering out|tempers out]] 32805/32768 ([[schisma]]), 78732/78125 ([[sensipent comma]]), 393216/390625 ([[würschmidt comma]]), and {{monzo| -13 17 -6 }} ([[graviton]]). In the [[7-limit]], there are two different maps; the first is {{val| 65 103 151 '''182''' }} (65), tempering out [[126/125]], [[245/243]] and [[686/675]], so that it [[support]]s [[sensi]], and the second is {{val| 65 103 151 '''183''' }} (65d), tempering out [[225/224]], [[3125/3087]], [[4000/3969]] and [[5120/5103]], so that it supports [[garibaldi]]. In both cases, the tuning privileges the [[5-limit]] over the 7-limit, as the 5-limit of 65 is quite accurate. The same can be said for the two different versions of 7-limit [[würschmidt]] temperament (wurschmidt and worschmidt) these two mappings provide. | |||
65edo approximates the intervals [[3/2]], [[5/4]], [[11/8]], [[19/16]], [[23/16]], [[31/16]] and [[47/32]] well, so that it does a good job representing the 2.3.5.11.19.23.31.47 [[just intonation subgroup]]. To this one may want to add [[17/16]], [[29/16]] and [[43/32]], giving the [[47-limit]] no-7's no-13's no-37's no-41's subgroup 2.3.5.11.17.19.23.29.31.43.47. In this sense it is a tuning of [[schismic]]/[[nestoria]] that focuses on the very primes that [[53edo]] neglects (which instead elegantly connects primes 7, 13, 37, and 41 to nestoria). Also of interest is the [[19-limit]] [[k*N subgroups|2*65 subgroup]] 2.3.5.49.11.91.119.19, on which 65 has the same tuning and commas as the [[zeta]] edo [[130edo]]. | |||
=== Prime harmonics === | |||
{{Harmonics in equal|65|intervals=prime|columns=15}} | |||
65edo contains [[13edo]] as | === Subsets and supersets === | ||
65edo contains [[5edo]] and [[13edo]] as subsets. The offset between a just perfect fifth at 702 cents and the 13edo superfifth at 738.5 cents, is approximately 2 degrees of 65edo. Therefore, an instrument fretted to 13edo, with open strings tuned to 3-limit intervals such as 4/3, 3/2, 9/8, 16/9 etc, will approximate a subset of 65edo. For an example of this, see [[Andrew Heathwaite]]'s composition [https://soundcloud.com/andrew_heathwaite/rubble-a-xenuke-unfolded ''Rubble: a Xenuke Unfolded'']. | |||
[[130edo]], which doubles its, corrects its approximation to harmonics 7 and 13. | |||
= | == Intervals == | ||
[[ | {| class="wikitable center-all right-2 left-3" | ||
|- | |||
! # | |||
! [[Cent]]s | |||
! Approximate ratios<ref group="note">{{sg|limit=2.3.5.11.13/7.17.19.23.29.31.47 subgroup}}</ref> | |||
! colspan="2" | [[Ups and downs notation]] | |||
|- | |||
| 0 | |||
| 0.00 | |||
| 1/1 | |||
| P1 | |||
| D | |||
|- | |||
| 1 | |||
| 18.46 | |||
| 81/80, 88/87, 93/92, 94/93, 95/94, 96/95, 100/99, 121/120, 115/114, 116/115, 125/124 | |||
| ^1 | |||
| ^D | |||
|- | |||
| 2 | |||
| 36.92 | |||
| 45/44, 46/45, 47/46, 48/47, 55/54, 128/125 | |||
| ^^1 | |||
| ^^D | |||
|- | |||
| 3 | |||
| 55.38 | |||
| 30/29, 31/30, 32/31, 33/32, 34/33 | |||
| vvm2 | |||
| vvEb | |||
|- | |||
| 4 | |||
| 73.85 | |||
| 23/22, 24/23, 25/24, 47/45 | |||
| vm2 | |||
| vEb | |||
|- | |||
| 5 | |||
| 92.31 | |||
| 18/17, 19/18, 20/19, 58/55, 135/128, 256/243 | |||
| m2 | |||
| Eb | |||
|- | |||
| 6 | |||
| 110.77 | |||
| 16/15, 17/16, 33/31 | |||
| A1/^m2 | |||
| D#/^Eb | |||
|- | |||
| 7 | |||
| 129.23 | |||
| 14/13, 27/25, 55/51 | |||
| v~2 | |||
| ^^Eb | |||
|- | |||
| 8 | |||
| 147.69 | |||
| 12/11, 25/23 | |||
| ~2 | |||
| vvvE | |||
|- | |||
| 9 | |||
| 166.15 | |||
| 11/10, 32/29 | |||
| ^~2 | |||
| vvE | |||
|- | |||
| 10 | |||
| 184.62 | |||
| 10/9, 19/17 | |||
| vM2 | |||
| vE | |||
|- | |||
| 11 | |||
| 203.08 | |||
| 9/8, 64/57 | |||
| M2 | |||
| E | |||
|- | |||
| 12 | |||
| 221.54 | |||
| 17/15, 25/22, 33/29, 58/51 | |||
| ^M2 | |||
| ^E | |||
|- | |||
| 13 | |||
| 240.00 | |||
| 23/20, 31/27, 38/33, 54/47, 55/48 | |||
| ^^M2 | |||
| ^^E | |||
|- | |||
| 14 | |||
| 258.46 | |||
| 22/19, 29/25, 36/31, 64/55 | |||
| vvm3 | |||
| vvF | |||
|- | |||
| 15 | |||
| 276.92 | |||
| 20/17, 27/23, 34/29, 75/64 | |||
| vm3 | |||
| vF | |||
|- | |||
| 16 | |||
| 295.38 | |||
| 19/16, 32/27 | |||
| m3 | |||
| F | |||
|- | |||
| 17 | |||
| 313.85 | |||
| 6/5, 55/46 | |||
| ^m3 | |||
| ^F | |||
|- | |||
| 18 | |||
| 332.31 | |||
| 23/19, 40/33 | |||
| v~3 | |||
| ^^F | |||
|- | |||
| 19 | |||
| 350.77 | |||
| 11/9, 27/22, 38/31 | |||
| ~3 | |||
| ^^^F | |||
|- | |||
| 20 | |||
| 369.23 | |||
| 26/21, 47/38, 68/55 | |||
| ^~3 | |||
| vvF# | |||
|- | |||
| 21 | |||
| 387.69 | |||
| 5/4, 64/51 | |||
| vM3 | |||
| vF# | |||
|- | |||
| 22 | |||
| 406.15 | |||
| 19/15, 24/19, 29/23, 34/27, 81/64 | |||
| M3 | |||
| F# | |||
|- | |||
| 23 | |||
| 424.62 | |||
| 23/18, 32/25 | |||
| ^M3 | |||
| ^F# | |||
|- | |||
| 24 | |||
| 443.08 | |||
| 22/17, 31/24, 40/31, 128/99 | |||
| ^^M3 | |||
| ^^F# | |||
|- | |||
| 25 | |||
| 461.54 | |||
| 30/23, 47/36, 72/55 | |||
| vv4 | |||
| vvG | |||
|- | |||
| 26 | |||
| 480.00 | |||
| 29/22, 33/25, 62/47 | |||
| v4 | |||
| vG | |||
|- | |||
| 27 | |||
| 498.46 | |||
| 4/3 | |||
| P4 | |||
| G | |||
|- | |||
| 28 | |||
| 516.92 | |||
| 23/17, 27/20, 31/23 | |||
| ^4 | |||
| ^G | |||
|- | |||
| 29 | |||
| 535.38 | |||
| 15/11, 34/25, 64/47 | |||
| v~4 | |||
| ^^G | |||
|- | |||
| 30 | |||
| 553.85 | |||
| 11/8, 40/29, 62/45 | |||
| ~4 | |||
| ^^^G | |||
|- | |||
| 31 | |||
| 572.31 | |||
| 25/18, 32/23 | |||
| ^~4/vd5 | |||
| vvG#/vAb | |||
|- | |||
| 32 | |||
| 590.77 | |||
| 24/17, 31/22, 38/27, 45/32 | |||
| vA4/d5 | |||
| vG#/Ab | |||
|- | |||
| 33 | |||
| 609.23 | |||
| 17/12, 27/19, 44/31, 64/45 | |||
| A4/^d5 | |||
| G#/^Ab | |||
|- | |||
| 34 | |||
| 627.69 | |||
| 36/25, 23/16 | |||
| ^A4/v~5 | |||
| ^G#/^^Ab | |||
|- | |||
| 35 | |||
| 646.15 | |||
| 16/11, 29/20, 45/31 | |||
| ~5 | |||
| vvvA | |||
|- | |||
| 36 | |||
| 664.62 | |||
| 22/15, 25/17, 47/32 | |||
| ^~5 | |||
| vvA | |||
|- | |||
| 37 | |||
| 683.08 | |||
| 34/23, 40/27, 46/31 | |||
| v5 | |||
| vA | |||
|- | |||
| 38 | |||
| 701.54 | |||
| 3/2 | |||
| P5 | |||
| A | |||
|- | |||
| 39 | |||
| 720.00 | |||
| 44/29, 50/33, 47/31 | |||
| ^5 | |||
| ^A | |||
|- | |||
| 40 | |||
| 738.46 | |||
| 23/15, 55/36, 72/47 | |||
| ^^5 | |||
| ^^A | |||
|- | |||
| 41 | |||
| 756.92 | |||
| 17/11, 48/31, 31/20, 99/64 | |||
| vvm6 | |||
| vvBb | |||
|- | |||
| 42 | |||
| 775.38 | |||
| 25/16, 36/23 | |||
| vm6 | |||
| vBb | |||
|- | |||
| 43 | |||
| 793.85 | |||
| 19/12, 27/17, 30/19, 46/29, 128/81 | |||
| m6 | |||
| Bb | |||
|- | |||
| 44 | |||
| 812.31 | |||
| 8/5, 51/32 | |||
| ^m6 | |||
| ^Bb | |||
|- | |||
| 45 | |||
| 830.77 | |||
| 21/13, 55/34, 76/47 | |||
| v~6 | |||
| ^^Bb | |||
|- | |||
| 46 | |||
| 849.23 | |||
| 18/11, 31/19, 44/27 | |||
| ~6 | |||
| vvvB | |||
|- | |||
| 47 | |||
| 867.69 | |||
| 33/20, 38/23 | |||
| ^~6 | |||
| vvB | |||
|- | |||
| 48 | |||
| 886.15 | |||
| 5/3, 92/55 | |||
| vM6 | |||
| vB | |||
|- | |||
| 49 | |||
| 904.62 | |||
| 27/16, 32/19 | |||
| M6 | |||
| B | |||
|- | |||
| 50 | |||
| 923.08 | |||
| 17/10, 29/17, 46/27, 128/75 | |||
| ^M6 | |||
| ^B | |||
|- | |||
| 51 | |||
| 941.54 | |||
| 19/11, 31/18, 50/29, 55/32 | |||
| ^^M6 | |||
| ^^B | |||
|- | |||
| 52 | |||
| 960.00 | |||
| 33/19, 40/23, 47/27, 54/31, 96/55 | |||
| vvm7 | |||
| vvC | |||
|- | |||
| 53 | |||
| 978.46 | |||
| 30/17, 44/25, 51/29, 58/33 | |||
| vm7 | |||
| vC | |||
|- | |||
| 54 | |||
| 996.92 | |||
| 16/9, 57/32 | |||
| m7 | |||
| C | |||
|- | |||
| 55 | |||
| 1015.38 | |||
| 9/5, 34/19 | |||
| ^m7 | |||
| ^C | |||
|- | |||
| 56 | |||
| 1033.85 | |||
| 20/11, 29/16 | |||
| v~7 | |||
| ^^C | |||
|- | |||
| 57 | |||
| 1052.31 | |||
| 11/6, 46/25 | |||
| ~7 | |||
| ^^^C | |||
|- | |||
| 58 | |||
| 1070.77 | |||
| 13/7, 50/27, 102/55 | |||
| ^~7 | |||
| vvC# | |||
|- | |||
| 59 | |||
| 1089.23 | |||
| 15/8, 32/17, 62/33 | |||
| vM7 | |||
| vC# | |||
|- | |||
| 60 | |||
| 1107.69 | |||
| 17/9, 19/10, 36/19, 55/29, 243/128, 256/135 | |||
| M7 | |||
| C# | |||
|- | |||
| 61 | |||
| 1126.15 | |||
| 23/12, 44/23, 48/25, 90/47 | |||
| ^M7 | |||
| ^C# | |||
|- | |||
| 62 | |||
| 1144.62 | |||
| 29/15, 31/16, 33/17, 60/31, 64/33 | |||
| ^^M7 | |||
| ^^C# | |||
|- | |||
| 63 | |||
| 1163.08 | |||
| 45/23, 47/24, 88/45, 92/47, 108/55, 125/64 | |||
| vv8 | |||
| vvD | |||
|- | |||
| 64 | |||
| 1181.54 | |||
| 87/55, 93/47, 95/48, 99/50, 115/58, 160/81, 184/93, 188/95, 228/115, 240/121, 248/125 | |||
| v8 | |||
| vD | |||
|- | |||
| 65 | |||
| 1200.00 | |||
| 2/1 | |||
| P8 | |||
| D | |||
|} | |||
<references group="note" /> | |||
== Notation == | |||
=== Ups and downs notation === | |||
65edo can be notated with ups and downs, spoken as up, dup, trup, dudsharp, downsharp, sharp, upsharp etc. and down, dud, trud, dupflat etc. | |||
{{Sharpness-sharp6a}} | |||
Half-sharps and half-flats can be used to avoid triple arrows: | |||
{{Sharpness-sharp6b}} | |||
[[Alternative symbols for ups and downs notation#Sharp-6| Alternative ups and downs]] have arrows borrowed from extended [[Helmholtz–Ellis notation]]: | |||
{{Sharpness-sharp6}} | |||
If double arrows are not desirable, arrows can be attached to quarter-tone accidentals: | |||
{{Sharpness-sharp6-qt}} | |||
=== Ivan Wyschnegradsky's notation === | |||
Since a sharp raises by six steps, Wyschnegradsky accidentals borrowed from [[72edo]] can also be used: | |||
{{sharpness-sharp6-iw}} | |||
=== Sagittal notation === | |||
This notation uses the same sagittal sequence as EDOs [[72edo#Sagittal notation|72]] and [[79edo#Sagittal notation|79]]. | |||
==== Evo flavor ==== | |||
<imagemap> | |||
File:65-EDO_Evo_Sagittal.svg | |||
desc none | |||
rect 80 0 300 50 [[Sagittal_notation]] | |||
rect 300 0 655 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation] | |||
rect 20 80 120 106 [[81/80]] | |||
rect 120 80 220 106 [[64/63]] | |||
rect 220 80 340 106 [[33/32]] | |||
default [[File:65-EDO_Evo_Sagittal.svg]] | |||
</imagemap> | |||
==== Revo flavor ==== | |||
<imagemap> | |||
File:65-EDO_Revo_Sagittal.svg | |||
desc none | |||
rect 80 0 300 50 [[Sagittal_notation]] | |||
rect 300 0 650 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation] | |||
rect 20 80 120 106 [[81/80]] | |||
rect 120 80 220 106 [[64/63]] | |||
rect 220 80 340 106 [[33/32]] | |||
default [[File:65-EDO_Revo_Sagittal.svg]] | |||
</imagemap> | |||
==== Evo-SZ flavor ==== | |||
<imagemap> | |||
File:65-EDO_Evo-SZ_Sagittal.svg | |||
desc none | |||
rect 80 0 300 50 [[Sagittal_notation]] | |||
rect 300 0 639 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation] | |||
rect 20 80 120 106 [[81/80]] | |||
rect 120 80 220 106 [[64/63]] | |||
rect 220 80 340 106 [[33/32]] | |||
default [[File:65-EDO_Evo-SZ_Sagittal.svg]] | |||
</imagemap> | |||
== Approximation to JI == | |||
=== Zeta peak index === | |||
{{ZPI | |||
| zpi = 334 | |||
| steps = 65.0158450885860 | |||
| step size = 18.4570391781413 | |||
| tempered height = 7.813349 | |||
| pure height = 7.642373 | |||
| integral = 1.269821 | |||
| gap = 16.514861 | |||
| octave = 1199.70754657919 | |||
| consistent = 6 | |||
| distinct = 6 | |||
}} | |||
== Regular temperament properties == | |||
{| class="wikitable center-4 center-5 center-6" | |||
|- | |||
! rowspan="2" | [[Subgroup]] | |||
! rowspan="2" | [[Comma list]] | |||
! rowspan="2" | [[Mapping]] | |||
! rowspan="2" | Optimal<br>8ve stretch (¢) | |||
! colspan="2" | Tuning error | |||
|- | |||
! [[TE error|Absolute]] (¢) | |||
! [[TE simple badness|Relative]] (%) | |||
|- | |||
| 2.3 | |||
| {{monzo| -103 65 }} | |||
| {{mapping| 65 103 }} | |||
| +0.131 | |||
| 0.131 | |||
| 0.71 | |||
|- | |||
| 2.3.5 | |||
| 32805/32768, 78732/78125 | |||
| {{mapping| 65 103 151 }} | |||
| −0.110 | |||
| 0.358 | |||
| 1.94 | |||
|- | |||
| 2.3.5.11 | |||
| 243/242, 4000/3993, 5632/5625 | |||
| {{mapping| 65 103 151 225 }} | |||
| −0.266 | |||
| 0.410 | |||
| 2.22 | |||
|} | |||
=== Rank-2 temperaments === | |||
{| class="wikitable center-all left-5" | |||
|+ style="font-size: 105%;" | Table of rank-2 temperaments by generator | |||
|- | |||
! Periods<br>per 8ve | |||
! Generator* | |||
! Cents* | |||
! Associated<br>ratio* | |||
! Temperament | |||
|- | |||
| 1 | |||
| 3\65 | |||
| 55.38 | |||
| 33/32 | |||
| [[Escapade]] | |||
|- | |||
| 1 | |||
| 9\65 | |||
| 166.15 | |||
| 11/10 | |||
| [[Squirrel]] etc. | |||
|- | |||
| 1 | |||
| 12\65 | |||
| 221.54 | |||
| 25/22 | |||
| [[Hemisensi]] | |||
|- | |||
| 1 | |||
| 19\65 | |||
| 350.77 | |||
| 11/9 | |||
| [[Karadeniz]] | |||
|- | |||
| 1 | |||
| 21\65 | |||
| 387.69 | |||
| 5/4 | |||
| [[Würschmidt]] | |||
|- | |||
| 1 | |||
| 24\65 | |||
| 443.08 | |||
| 162/125 | |||
| [[Sensipent]] | |||
|- | |||
| 1 | |||
| 27\65 | |||
| 498.46 | |||
| 4/3 | |||
| [[Helmholtz (temperament)|Helmholtz]] / [[nestoria]] / [[photia]] | |||
|- | |||
| 1 | |||
| 28\65 | |||
| 516.92 | |||
| 27/20 | |||
| [[Larry]] | |||
|- | |||
| 5 | |||
| 20\65<br>(6\65) | |||
| 369.23<br>(110.77) | |||
| 99/80<br>(16/15) | |||
| [[Quintosec]] | |||
|- | |||
| 5 | |||
| 27\65<br>(1\65) | |||
| 498.46<br>(18.46) | |||
| 4/3<br>(81/80) | |||
| [[Quintile]] | |||
|- | |||
| 5 | |||
| 30\65<br>(4\65) | |||
| 553.85<br>(73.85) | |||
| 11/8<br>(25/24) | |||
| [[Countdown]] | |||
|} | |||
<nowiki/>* [[Normal lists|Octave-reduced form]], reduced to the first half-octave, and [[Normal lists|minimal form]] in parentheses if distinct | |||
== Scales == | |||
* Amulet{{idiosyncratic}}, (approximated from [[25edo]], subset of [[würschmidt]]): 5 3 5 5 3 5 12 5 5 3 5 12 5 | |||
* [[Photia7]] | |||
* [[Photia12]] | |||
* [[Skateboard7]] | |||
== Instruments == | |||
[[Lumatone mapping for 65edo]] | |||
== Music == | |||
; [[Bryan Deister]] | |||
* [https://www.youtube.com/shorts/W5PXWFduPco ''microtonal improvisation in 65edo''] (2025). | |||
[[Category:Listen]] | |||
[[Category:Schismic]] | |||
[[Category:Sensipent]] | |||
[[Category:Subgroup temperaments]] | |||
[[Category:Würschmidt]] | |||
Latest revision as of 08:08, 22 July 2025
| ← 64edo | 65edo | 66edo → |
65 equal divisions of the octave (abbreviated 65edo or 65ed2), also called 65-tone equal temperament (65tet) or 65 equal temperament (65et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 65 equal parts of about 18.5 ¢ each. Each step represents a frequency ratio of 21/65, or the 65th root of 2.
Theory
65et can be characterized as the temperament which tempers out 32805/32768 (schisma), 78732/78125 (sensipent comma), 393216/390625 (würschmidt comma), and [-13 17 -6⟩ (graviton). In the 7-limit, there are two different maps; the first is ⟨65 103 151 182] (65), tempering out 126/125, 245/243 and 686/675, so that it supports sensi, and the second is ⟨65 103 151 183] (65d), tempering out 225/224, 3125/3087, 4000/3969 and 5120/5103, so that it supports garibaldi. In both cases, the tuning privileges the 5-limit over the 7-limit, as the 5-limit of 65 is quite accurate. The same can be said for the two different versions of 7-limit würschmidt temperament (wurschmidt and worschmidt) these two mappings provide.
65edo approximates the intervals 3/2, 5/4, 11/8, 19/16, 23/16, 31/16 and 47/32 well, so that it does a good job representing the 2.3.5.11.19.23.31.47 just intonation subgroup. To this one may want to add 17/16, 29/16 and 43/32, giving the 47-limit no-7's no-13's no-37's no-41's subgroup 2.3.5.11.17.19.23.29.31.43.47. In this sense it is a tuning of schismic/nestoria that focuses on the very primes that 53edo neglects (which instead elegantly connects primes 7, 13, 37, and 41 to nestoria). Also of interest is the 19-limit 2*65 subgroup 2.3.5.49.11.91.119.19, on which 65 has the same tuning and commas as the zeta edo 130edo.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | 41 | 43 | 47 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.00 | -0.42 | +1.38 | -8.83 | +2.53 | +8.70 | +5.81 | -2.13 | -0.58 | +4.27 | -0.42 | +7.12 | -4.45 | +5.41 | -0.89 |
| Relative (%) | +0.0 | -2.3 | +7.5 | -47.8 | +13.7 | +47.1 | +31.5 | -11.5 | -3.2 | +23.1 | -2.3 | +38.6 | -24.1 | +29.3 | -4.8 | |
| Steps (reduced) |
65 (0) |
103 (38) |
151 (21) |
182 (52) |
225 (30) |
241 (46) |
266 (6) |
276 (16) |
294 (34) |
316 (56) |
322 (62) |
339 (14) |
348 (23) |
353 (28) |
361 (36) | |
Subsets and supersets
65edo contains 5edo and 13edo as subsets. The offset between a just perfect fifth at 702 cents and the 13edo superfifth at 738.5 cents, is approximately 2 degrees of 65edo. Therefore, an instrument fretted to 13edo, with open strings tuned to 3-limit intervals such as 4/3, 3/2, 9/8, 16/9 etc, will approximate a subset of 65edo. For an example of this, see Andrew Heathwaite's composition Rubble: a Xenuke Unfolded.
130edo, which doubles its, corrects its approximation to harmonics 7 and 13.
Intervals
| # | Cents | Approximate ratios[note 1] | Ups and downs notation | |
|---|---|---|---|---|
| 0 | 0.00 | 1/1 | P1 | D |
| 1 | 18.46 | 81/80, 88/87, 93/92, 94/93, 95/94, 96/95, 100/99, 121/120, 115/114, 116/115, 125/124 | ^1 | ^D |
| 2 | 36.92 | 45/44, 46/45, 47/46, 48/47, 55/54, 128/125 | ^^1 | ^^D |
| 3 | 55.38 | 30/29, 31/30, 32/31, 33/32, 34/33 | vvm2 | vvEb |
| 4 | 73.85 | 23/22, 24/23, 25/24, 47/45 | vm2 | vEb |
| 5 | 92.31 | 18/17, 19/18, 20/19, 58/55, 135/128, 256/243 | m2 | Eb |
| 6 | 110.77 | 16/15, 17/16, 33/31 | A1/^m2 | D#/^Eb |
| 7 | 129.23 | 14/13, 27/25, 55/51 | v~2 | ^^Eb |
| 8 | 147.69 | 12/11, 25/23 | ~2 | vvvE |
| 9 | 166.15 | 11/10, 32/29 | ^~2 | vvE |
| 10 | 184.62 | 10/9, 19/17 | vM2 | vE |
| 11 | 203.08 | 9/8, 64/57 | M2 | E |
| 12 | 221.54 | 17/15, 25/22, 33/29, 58/51 | ^M2 | ^E |
| 13 | 240.00 | 23/20, 31/27, 38/33, 54/47, 55/48 | ^^M2 | ^^E |
| 14 | 258.46 | 22/19, 29/25, 36/31, 64/55 | vvm3 | vvF |
| 15 | 276.92 | 20/17, 27/23, 34/29, 75/64 | vm3 | vF |
| 16 | 295.38 | 19/16, 32/27 | m3 | F |
| 17 | 313.85 | 6/5, 55/46 | ^m3 | ^F |
| 18 | 332.31 | 23/19, 40/33 | v~3 | ^^F |
| 19 | 350.77 | 11/9, 27/22, 38/31 | ~3 | ^^^F |
| 20 | 369.23 | 26/21, 47/38, 68/55 | ^~3 | vvF# |
| 21 | 387.69 | 5/4, 64/51 | vM3 | vF# |
| 22 | 406.15 | 19/15, 24/19, 29/23, 34/27, 81/64 | M3 | F# |
| 23 | 424.62 | 23/18, 32/25 | ^M3 | ^F# |
| 24 | 443.08 | 22/17, 31/24, 40/31, 128/99 | ^^M3 | ^^F# |
| 25 | 461.54 | 30/23, 47/36, 72/55 | vv4 | vvG |
| 26 | 480.00 | 29/22, 33/25, 62/47 | v4 | vG |
| 27 | 498.46 | 4/3 | P4 | G |
| 28 | 516.92 | 23/17, 27/20, 31/23 | ^4 | ^G |
| 29 | 535.38 | 15/11, 34/25, 64/47 | v~4 | ^^G |
| 30 | 553.85 | 11/8, 40/29, 62/45 | ~4 | ^^^G |
| 31 | 572.31 | 25/18, 32/23 | ^~4/vd5 | vvG#/vAb |
| 32 | 590.77 | 24/17, 31/22, 38/27, 45/32 | vA4/d5 | vG#/Ab |
| 33 | 609.23 | 17/12, 27/19, 44/31, 64/45 | A4/^d5 | G#/^Ab |
| 34 | 627.69 | 36/25, 23/16 | ^A4/v~5 | ^G#/^^Ab |
| 35 | 646.15 | 16/11, 29/20, 45/31 | ~5 | vvvA |
| 36 | 664.62 | 22/15, 25/17, 47/32 | ^~5 | vvA |
| 37 | 683.08 | 34/23, 40/27, 46/31 | v5 | vA |
| 38 | 701.54 | 3/2 | P5 | A |
| 39 | 720.00 | 44/29, 50/33, 47/31 | ^5 | ^A |
| 40 | 738.46 | 23/15, 55/36, 72/47 | ^^5 | ^^A |
| 41 | 756.92 | 17/11, 48/31, 31/20, 99/64 | vvm6 | vvBb |
| 42 | 775.38 | 25/16, 36/23 | vm6 | vBb |
| 43 | 793.85 | 19/12, 27/17, 30/19, 46/29, 128/81 | m6 | Bb |
| 44 | 812.31 | 8/5, 51/32 | ^m6 | ^Bb |
| 45 | 830.77 | 21/13, 55/34, 76/47 | v~6 | ^^Bb |
| 46 | 849.23 | 18/11, 31/19, 44/27 | ~6 | vvvB |
| 47 | 867.69 | 33/20, 38/23 | ^~6 | vvB |
| 48 | 886.15 | 5/3, 92/55 | vM6 | vB |
| 49 | 904.62 | 27/16, 32/19 | M6 | B |
| 50 | 923.08 | 17/10, 29/17, 46/27, 128/75 | ^M6 | ^B |
| 51 | 941.54 | 19/11, 31/18, 50/29, 55/32 | ^^M6 | ^^B |
| 52 | 960.00 | 33/19, 40/23, 47/27, 54/31, 96/55 | vvm7 | vvC |
| 53 | 978.46 | 30/17, 44/25, 51/29, 58/33 | vm7 | vC |
| 54 | 996.92 | 16/9, 57/32 | m7 | C |
| 55 | 1015.38 | 9/5, 34/19 | ^m7 | ^C |
| 56 | 1033.85 | 20/11, 29/16 | v~7 | ^^C |
| 57 | 1052.31 | 11/6, 46/25 | ~7 | ^^^C |
| 58 | 1070.77 | 13/7, 50/27, 102/55 | ^~7 | vvC# |
| 59 | 1089.23 | 15/8, 32/17, 62/33 | vM7 | vC# |
| 60 | 1107.69 | 17/9, 19/10, 36/19, 55/29, 243/128, 256/135 | M7 | C# |
| 61 | 1126.15 | 23/12, 44/23, 48/25, 90/47 | ^M7 | ^C# |
| 62 | 1144.62 | 29/15, 31/16, 33/17, 60/31, 64/33 | ^^M7 | ^^C# |
| 63 | 1163.08 | 45/23, 47/24, 88/45, 92/47, 108/55, 125/64 | vv8 | vvD |
| 64 | 1181.54 | 87/55, 93/47, 95/48, 99/50, 115/58, 160/81, 184/93, 188/95, 228/115, 240/121, 248/125 | v8 | vD |
| 65 | 1200.00 | 2/1 | P8 | D |
- ↑ Based on treating 65edo as a 2.3.5.11.13/7.17.19.23.29.31.47 subgroup temperament; other approaches are also possible.
Notation
Ups and downs notation
65edo can be notated with ups and downs, spoken as up, dup, trup, dudsharp, downsharp, sharp, upsharp etc. and down, dud, trud, dupflat etc.
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |||||||||||||
| Flat symbol |
Half-sharps and half-flats can be used to avoid triple arrows:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |||||||||||||
| Flat symbol |
Alternative ups and downs have arrows borrowed from extended Helmholtz–Ellis notation:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Flat symbol | |
|
|
|
|
|
|
|
|
|
|
|
|
|
If double arrows are not desirable, arrows can be attached to quarter-tone accidentals:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
|
|
|
|
|
|
| |
| Flat symbol | |
|
|
|
|
|
|
|
|
|
|
|
|
Ivan Wyschnegradsky's notation
Since a sharp raises by six steps, Wyschnegradsky accidentals borrowed from 72edo can also be used:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
|
|
|
|
|
| ||
| Flat symbol | |
|
|
|
|
|
|
|
|
|
|
|
Sagittal notation
This notation uses the same sagittal sequence as EDOs 72 and 79.
Evo flavor

Revo flavor

Evo-SZ flavor

Approximation to JI
Zeta peak index
| Tuning | Strength | Octave (cents) | Integer limit | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ZPI | Steps per 8ve |
Step size (cents) |
Height | Integral | Gap | Size | Stretch | Consistent | Distinct | |
| Tempered | Pure | |||||||||
| 334zpi | 65.015845 | 18.457039 | 7.813349 | 7.642373 | 1.269821 | 16.514861 | 1199.707547 | −0.292453 | 6 | 6 |
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3 | [-103 65⟩ | [⟨65 103]] | +0.131 | 0.131 | 0.71 |
| 2.3.5 | 32805/32768, 78732/78125 | [⟨65 103 151]] | −0.110 | 0.358 | 1.94 |
| 2.3.5.11 | 243/242, 4000/3993, 5632/5625 | [⟨65 103 151 225]] | −0.266 | 0.410 | 2.22 |
Rank-2 temperaments
| Periods per 8ve |
Generator* | Cents* | Associated ratio* |
Temperament |
|---|---|---|---|---|
| 1 | 3\65 | 55.38 | 33/32 | Escapade |
| 1 | 9\65 | 166.15 | 11/10 | Squirrel etc. |
| 1 | 12\65 | 221.54 | 25/22 | Hemisensi |
| 1 | 19\65 | 350.77 | 11/9 | Karadeniz |
| 1 | 21\65 | 387.69 | 5/4 | Würschmidt |
| 1 | 24\65 | 443.08 | 162/125 | Sensipent |
| 1 | 27\65 | 498.46 | 4/3 | Helmholtz / nestoria / photia |
| 1 | 28\65 | 516.92 | 27/20 | Larry |
| 5 | 20\65 (6\65) |
369.23 (110.77) |
99/80 (16/15) |
Quintosec |
| 5 | 27\65 (1\65) |
498.46 (18.46) |
4/3 (81/80) |
Quintile |
| 5 | 30\65 (4\65) |
553.85 (73.85) |
11/8 (25/24) |
Countdown |
* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct
Scales
- Amulet[idiosyncratic term], (approximated from 25edo, subset of würschmidt): 5 3 5 5 3 5 12 5 5 3 5 12 5
- Photia7
- Photia12
- Skateboard7