User:Aura/Aura's Ideas on Functional Harmony (Part 1): Difference between revisions
No edit summary |
Found a better follow-up to a sycophant chord that stays in key. |
||
| (184 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
One construct from Western Classical music with potential implications for Microtonalists is '''[[Wikipedia:Function (music)|harmonic function]]'''- especially as it pertains to the [[5L 2s|diatonic]] MOS scale and its various relatives. | One construct from Western Classical music with potential implications for Microtonalists is '''[[Wikipedia:Function (music)|harmonic function]]'''- especially as it pertains to the [[5L 2s|diatonic]] MOS scale and its various relatives. In Mainstream Music Theory there were once two prevailing schools of thought in regards to diatonic functional harmony- '''[[Wikipedia:Function (music) #German functional theory|German Theory]]''' and '''[[Wikipedia:Function (music) #Viennese theory of the degrees|Viennese Theory]]'''- however, in a conversation with [[User:Mousemambo|Mousemambo]] on Discord, it has been revealed to me that in modern practice, the old ideas of functional harmony have largely disintegrated due firstly to the conviction that after around 1900 CE, art music took a turn away from Common Practice Period foundations and those old analyses just don't work anymore as originally formulated, and secondly due to a suspicion that they never really existed beyond the pareidolia of minds trying to see patterns in noise. Mousemambo has also pointed out to me that modern writers have moved away from the convoluted depths of the two Germanic schools, now more often simply identifying scale degrees and the chords for which they are the root as either Tonic; Dominant, which is basically anything leading to Tonic; and Predominant, which is basically anything leading to Dominant. However, upon listening to the ways in which Plagal cadences get used, and how the chords on the perfect 4th above the Tonic get used as a sort of "home away from home" in some tunings, it is obvious to me that the stance taken by modern writers is an oversimplification, and that there are more remnants of the ideas of the two schools in modern music than one would initially think. Furthermore, the genres of music I write call for a reconstruction of at least some of the ideals of the old Germanic schools from the ground up. Thus, ideas from both schools, as well as a number of other ideas, find a home in my microtonal theory and practice. If the reader will bear with me, I shall use narrative set-ups and character metaphors to describe how the various harmonic functions act in composition and the way they relate to one another, and, furthermore, I'll eventually be looking at ways to extend this reconstruction of functional harmony into the microtonal realm. However, before I get into that, I must answer a few questions about how function relates to different parts of the chord. | ||
== Harmonic Information, Tonic, and Chord Structure == | |||
In modern theory, it is often contended that the third is the most important scale degree for determining harmonic information, followed by the root and the seventh while the fifth is the least important, however, I disagree with this assessment. | |||
Instead, I contend that it's the root of a chord and the relationship between the chord root and the [[Tonic]] that dictates the bulk of the context for the function of the other notes in a given chord, with other bits of information being dictated by the relationship of other notes in the chord to both the Tonic and the actual chord root- do note that which note is considered to be the Tonic can in fact change based on additional context, such as the location of tritones- and, to a lesser extent, wolf fifths and wolf fourths- in a scale, as these, in combination with a tonality's direction of construction, can tonicize certain notes. From there, I think that only perfect fourths or perfect fifths that are either above or below a chord root can actually create stable frameworks for building chords, while dividing such intervals in two pieces without causing crowding creates the notes that impart character and color to chords. However, because perfect fifths are larger than perfect fourths, there's greater ease and a greater selection of options in dividing a perfect fifth without causing crowding than there is in doing the same with a perfect fourth. | |||
I must also admit that I think additional harmonic information can be supplied by the likes of both otonal and utonal [[primodality]], albeit my approach is a bit more unusual. While primes other than 2 can form the basis of tonality, it should be mentioned that the higher the prime involved as common numerator and or common denominator, the weaker the tonicization effect. Furthermore, I'm of the opinion that if you want to add intervals from segments with higher-prime denominators such as /3 or /5 to an otherwise /2^n segment to help flesh out what is essentially a Bass-Up tonality, it will usually work out best if that /3 or /5 interval is also a 2^n/ type of interval- in this case, 4/3 or 8/5. Similarly, I'm of the opinion that if you want to add intervals from segments with higher-prime denominators such as /5 or /7 to an otherwise /3*2^n segment to help flesh out what is essentially a Bass-Up tonality, it will usually work out best if that /5 or /7 interval is also a 3*2^n/ type of interval- in this case, 6/5 or 12/7. | |||
== Facets Derived from German Theory == | == Facets Derived from German Theory == | ||
Among the chief ideas that come from German Theory is that there are three basic, or primary functions, and that there are multiple operations that can be applied to these three basic functions in order to derive new functions. | Among the chief ideas that come from German Theory is that there are three basic, or primary functions, and that there are multiple operations that can be applied to these three basic functions in order to derive new functions. However, compared to those ideal functions, one of the three is in part original to my work. | ||
[[File:Diatonic Function Map (Version 4).png|thumb|Current diagram of diatonic and paradiatonic function locations as of the current edition of this article.]] | |||
=== Basic Diatonic Functions === | === Basic Diatonic Functions === | ||
The three basic functions have their roots in [[LCJI]] | The three basic functions have their roots in [[LCJI]]. The functions themselves are labeled as follows: | ||
'''Tonic''' - | '''[[Tonic]]''' - This functionality has its roots in the fundamental at the root of both the harmonic and subharmonic series, which for all intents and purposes, can be thought of as [[1/1]], and, in [[octave equivalence|octave equivalent]] systems, [[2/1]]. To use a character metaphor for how the Tonic acts in functional harmony, the Tonic is the king of the Kingdom of Tonality- a very good king who not only exercises the highest authority in matters of governing the kingdom and does not tolerate challenges to his leadership, but also knows how be a top-notch confidante to his subjects both wherever and whenever possible. For more specifics on the functions of the Tonic, see the linked article. | ||
'''Dominant''' - As per the name, and as noted on the [[Wikipedia:Dominant (music)|Wikipedia article]], the Dominant is the second most important after the Tonic, | '''Dominant''' - As per the name, and as noted on the [[Wikipedia:Dominant (music)|Wikipedia article]], the Dominant is the second most important after the Tonic, However, in contrast to what is stated about the Dominant in the article, there are several caveats which must be addressed in the realm of microtonality. Firstly, there's the matter of its origins- specifically, it is generated by the tonic as the first [[3-limit]] interval and indeed the first nontonic note in the "majoresque" direction. Secondly, there's the matter of just what it does, as it typically serves as one, or often more, of the following- a primary creator of instability in the "majoresque" direction that requires the Tonic for resolution, the second most important melodic and or harmonic anchor after the Tonic- a function that requires it to be tuned with a great deal of accuracy in order to blend well with the Tonic- as well as a generator of many of the "majoresque" notes in a [[5L 2s|diatonic MOS]], and or a discourager against the usage of other microtonally nearby pitches. Thirdly, one must take stock of the fact that, aside from the Unison and Octave, each octave-reduced harmonic and corresponding subharmonic interval come together to generate their own axis which has a preferred direction of travel<ref>[https://www.youtube.com/watch?v=HBdWxSxxe1M Quartertone Harmony - Beyond the Circle of Fifths SD 480p]</ref> which is determined by a Tonality's direction of construction. Finally, one must take stock of the fact that when you take the notes that occur before the Tonic on each of these axes when moving in the preferred direction of travel and place them in a sequence, one finds that a clear hierarchy of functional strength based on the closeness of harmonic and subharmonic connection to the Tonic becomes apparent, with the [[3/2]] Perfect 5th away from the Tonic in a tonality's direction of construction naturally emerging as the note with the strongest connection to the Tonic, though it should be noted that the relationships in this hierarchy are quite sensitive to detuning, and can even be scrambled by such detuning. Thus, the term "Dominant"- in its most basic form as referred to in this article, and specifically at the root level- is restricted to where it only refers to such notes that occur roughly at a 3/2 interval away from the Tonic in the scale's direction of construction, with acceptable detuning levels being at around 3.5 cents from JI on either side. On the chord level, not only is the root level definition of the Dominant function at play, but it should also be noted that the Dominant does not see the Tonic occurring in the proximal tertian structure of its chord- that is, as a third or fifth. To use a character metaphor for how the Dominant acts in functional harmony, the Dominant is both the Head Steward of the Tonic's castle, and the one that executes the Tonic's directives as a Manager of Civil Service in the Kingdom of Tonality. | ||
'''Serviant''' - Compared to the term "''Subdominant''" from | '''Serviant''' - Compared to the term "''Subdominant''" from music theory of old, the term "Serviant" (or, alternatively "Servient"), specifically at the root level, is restricted to those notes that occur roughly at a [[4/3]] interval away from the Tonic in the scale's direction of construction since the Serviant function is essentially the inverse of the Dominant function, and acts as a sort of counterweight to the Dominant relative to the Tonic. It typically serves as one, or often more, of the following— a primary creator of instability in the "minoresque" direction that can either be intensified with the dominant or resolved with the tonic, the third most important melodic and or harmonic anchor after the tonic and the dominant, a generator of many of the "minoresque" notes in a diatonic MOS, and or a discourager against the usage of other microtonally nearby pitches. To use a character metaphor for how the Serviant acts in functional harmony, the Serviant is a Servant who goes above and beyond the call of duty and acts as a confidante that observes things and reports back to the Dominant and Tonic about the way things are working both inside and outside the Tonic's castle due to its relationships to various Nontonic functions. Although one might think that the term "Subdominant" would be eligible for getting a similar treatment to the term "Dominant" here, the problems with such an option are threefold. Firstly, not all possible "Subdominant" harmonies have the same harmonic properties relative to the Tonic, as there is an extremely close connection between the Tonic and the 4/3 Perfect 4th. Secondly, in music built from the Treble downwards, the notes with these sorts of functions are actually located ''above'' the Dominant. Thirdly, in common parlance, "Subdominant" is often equated with "Predominant", however, while the Serviant does tend to resolve towards the Dominant, or else some other note that acts as a surrogate for the Dominant, the fact remains that it can also create plagal cadences, which break the modern Tonic-Dominant-Predominant paradigm and are better explained in part by the ideals of the two Germanic schools. On the chord level, not only is the root level definition of the Serviant function at play, but it should also be noted that a Serviant chord often sees the Tonic occurring in the proximal structure of its chord- that is, as either a third or fifth- which explains why Serviant chords are weaker than their Dominant counterparts in both Bass-Up and Treble-Down Tonalities. | ||
=== Basic Operations === | === Basic Diatonic Function-Deriving Operations === | ||
The way I see it, there are | The way I see it, there are seven known operations which can be used to derive additional diatonic functions from the three basic functions listed above. | ||
'''Stacking''' - The notes that are arrived at through stacking multiple instances of either 3/2 or 4/3 (or their tempered counterparts) are dubbed according to the number of instances stacked, and the nature of the notes separated by the interval being stacked. Thus, stacking two instances of the Dominant or the Serviant results in the creation of the " | '''Stacking''' - The notes that are arrived at through stacking multiple instances of either 3/2 or 4/3 (or their tempered counterparts) are dubbed according to the number of instances stacked, and the nature of the notes separated by the interval being stacked. Thus, stacking two instances of the Dominant or the Serviant results in the creation of the "Bidominant" or "Biserviant" respectively. This concept comes from the German language's way of referring to the chord built on the second scale degree of the Diatonic scale as the "Doppeldominante", which literally means "Double Dominant". | ||
'''Parallelism''' - Notes located in the same primary [[tetrachord]] as either the Tonic, the Dominant, or the Serviant take on similar functions to said notes, with the caveat that functions derived from the Tonic in this fashion are still technically | '''Parallelism''' - Notes located in the same primary [[tetrachord]] as either the Tonic, the Dominant, or the Serviant but that don't crowd them tend to take on similar functions to said notes, with the caveat that functions derived from the Tonic in this fashion are still technically Nontonic functions. This process is one of two that create what in traditional music theory are referred to as [[Wikipedia:Parallel and counter parallel|"''parallels''" and "''counter parallels''"]]. It should be noted that the ability of an interval to relate to the Tonic through Parallelism, as well as the surrounding of more dissonant intervals by consonant intervals in the same region displaying such relationships to the Tonic, results in a tendency towards harmonic stagnation. | ||
'''Adjacency''' - Notes within a suitable voice leading distance from either the Dominant or Serviant tend to have the opposite function relative to the Tonic- this process even extends to the relationship between the Dominant and Serviant themselves. This process is one of two that create what in traditional music theory are referred to as "''parallels''" and "''counter parallels''", however, unlike Parallelism proper, this process can establish these kinds of relationships outside the primary tetrachord. | '''Adjacency''' - Notes within a suitable voice leading distance from either the Dominant or Serviant tend to have the opposite function relative to the Tonic- this process even extends to the relationship between the Dominant and Serviant themselves. On the other hand, notes within this same kind of distance from the Tonic often tend to have their functions colored more by their relationships to both the Dominant and Serviant. This process is one of two that create what in traditional music theory are referred to as "''parallels''" and "''counter parallels''", however, unlike Parallelism proper, this process can establish these kinds of relationships outside the primary tetrachord. | ||
'''Antipodism''' - Notes that are either opposite in | '''Antipodism''' - Notes that are either opposite in pitch hue or nearly so due to being approximately half an octave away from the starting point are harmonically opposed to the starting point. Non-tonic notes related through this process tend to have the opposite function relative to the Tonic. For the notes related to the Tonic by this process, see Antitonic below. | ||
'''Preparation''' - Notes that "prepare the way" for either a Dominant or a Serviant through any of the above operations, or through some other mechanism, relate to said notes by this process. Functions which have this kind of role relative to some other function are denoted with a "pre-" prefix here. | |||
'''Detempering''' - When the comma or subchroma that separates a note from one of the three primary functions is not tempered out, it results in the appearance of notes with either similar functions to the Dominant or Serviant, or, in the case of this function being applied to the Tonic, a Nontonic function similar to one of the Chromatic functions. Often, though not always, these notes fall within the uncanny valleys of the three primary functions. | |||
'''Neutralization''' - When one hybridizes Major and Minor Diatonic scale degrees of the same class or even tempers them together, one is using this process. | |||
== Facets Derived from Viennese Theory == | == Facets Derived from Viennese Theory == | ||
Among the chief ideas that come from Viennese Theory is the idea that each degree has its own function relative to the Tonic. However, while in Viennese Theory proper, the degrees are strictly defined only relative to the cycle of fifths, I, for the realm of Microtonality, not only take stacks of 3/2 to form a key navigational axis called the "'''Diatonic Axis'''", but also additionally take things like Bass-Up | Among the chief ideas that come from Viennese Theory is the idea that each degree has its own function relative to the Tonic. However, while in Viennese Theory proper, the degrees are strictly defined only relative to the cycle of fifths, I, for the realm of Microtonality, not only take stacks of 3/2 to form a key navigational axis called the "'''Diatonic Axis'''", but also additionally take things like Bass-Up tonality (that is, tonal music built from the low pitches upwards) and Treble-Down tonality (that is, tonal music built from the high pitches downwards) into consideration. On top of that, I also contend that virtually all of the functions described by Viennese Theory find their roots in specific combinations of the different operations described above on the basic functions from German Theory. | ||
=== Derivative Diatonic Functions === | |||
I should point out that all of the scale degree functions described in Viennese Theory, as well as a few additional functions listed on this page, can be classified as '''first derivative''' functions because only one instance of any given derivational process is needed to reach them. Do note that of all the original Viennese functions, only the Mediant remains virtually unchanged from the original theories to this reconstruction, as another has been renamed, while others have been grouped together under new functions. | |||
'''Supervicinant''' - This is any note that maps to 1\7 above the Tonic, and in fact, intervals in this vicinity have both Tonic Adjacent and Serviant Parallel functions, beyond that, however, the precise behavior of notes in this range is determined by both mappings and concrete tuning ranges, see the Supervicinant and Subvicinant Subtypes section for more discussion of this function. | |||
'''Mediant''' - This is the note that maps to 2\7 from the Tonic in the scale's direction of construction and is named due to being roughly halfway between the Tonic and the Dominant. This is the first of the two diatonic scale degrees that are located relatively far from the Tonic along the Circle of Third Harmonics, and, as a consequence, not only has the most possibilities for realization, but also a tendency towards stagnation, leading to the historical designation as a "weak harmony". Aside from these, the properties that are central to the Mediant function are all most easily derived through the Tonic Parallel function and the Serviant Adjacent function, and in addition, Mediants have both Preserviant and Predominant functions. Furthermore, since there's such a large range of Mediants, there are a multitude of subtypes, see the Mediant Subtypes section for more discussion of this function. | |||
'''Antitonic''' - This is a special case, see the Antitonic Subtypes section for more discussion of this function. | |||
'''Contramediant''' - Compared to the term "''Submediant''" from traditional music theory, the term "Contramediant" may have a slightly different frame of reference, as while a "Submediant" is halfway between the Tonic and a "Subdominant", the "Contramediant" is halfway between the Tonic and the Serviant. The Contramediant is the note that maps to 5\7 from the Tonic in the scale's direction of construction, and is the second of two that are located relatively far from the Tonic along the Circle of Third Harmonics, and, as a consequence, is not only tied with the Mediant for having the most possibilities for realization, but also has a tendency towards stagnation, leading to the historical designation as a "weak harmony". From a functional standpoint, the properties that are central to the Contramediant function are most easily derived through the Tonic Parallel function and the Dominant Adjacent function, and in addition, Contramediants have both Preserviant and Predominant functions. Furthermore, since there's such a large range of Contramediants, there are a multitude of subtypes, see the Contramediant Subtypes section for more discussion of this function. | |||
'''Subvicinant''' - This is any note that maps to 1\7 below the Tonic, and in fact, intervals in this vicinity have both Tonic Adjacent and Dominant Parallel functions, beyond that, however, the precise behavior of notes in this range is determined by both mappings and concrete tuning ranges, see the Supervicinant and Subvicinant Subtypes section for more discussion of this function. | |||
== Supervicinant and Subvicinant Subtypes == | |||
The Supervicinant and Subvicinant functions each have two subtypes that are common to traditional music theory and one subtype that's not diatonic at all, although leading tones have been specified according to their position and have been given distinct functions. | |||
=== Specific Types of Supervicinant === | |||
The four subtypes of Supervicinant are as follows... | |||
'''Supercollocant''' - This subtype of Supervicinant, although not found in Viennese Theory proper, is an interval that usually maps to both 1\7 and 2\24 in Bass-Up tonality. Additionally, it has the Antidominant function as typified by the root of the [[Wikipedia:Neapolitan chord|Neapolitan chord]] in Bass-Up tonality and the Antiserviant function in Treble-Down tonality. In actuality, two subtypes of Supercollocant exist- the "'''Proximosupercollocant'''", which always maps to both 1\7 and 2\24 in Bass-Up tonality, and the "'''Distosupercollocant'''", which maps to 1\7 and either 2\24 or 3\24 depending on a variety of factors, and is distinct from both Proximosupercollocant and Superabrogant only in finer tuning systems where it is usually more consonant, and thus, weaker. An example of a Proximosupercollocant is [[256/243]] while an example of a Distosupercollocant is [[16/15]]. | |||
'''Superabrogant''' - This subtype of Supervicinant is not a traditional diatonic function at all since it is an interval that maps to both 1\7 and 3\24 in Bass-Up tonality. As per this function's name, the intervals in this range are like Supercollocants in that they may cause listeners to forget the ending pitch's relationship to the starting pitch in voice-leading. However, they are noticeably too wide for them to convincingly pass off as being totally semitone-like since they feel as if they're rather disconnected from the Tonic, and furthermore, the occurrence of two successive instances of these sorts of intervals in the same melodic line in the same direction is liable to come across as jarring. | |||
'''Superaequient''' - This subtype of Supervicinant is an interval that maps to 1\7 and either 3\24 or 4\24 depending on a variety of factors. It is so named for the [[equable heptatonic]] region above the Tonic, which comprises the bulk of its range, and for its capacity to straddle the line between the Supertonic and Superabrogant functions in voice-leading. Conspicuously, it is distinct from Supertonic and Superabrogant functions only in finer tuning systems, with the approximation ranges for [[11/10]] and [[10/9]] being located at its borders. | |||
'''Supertonic''' - This subtype of Supervicinant is an interval that maps to both 1\7 and 4\24 in Bass-Up tonality and occurs above the Tonic as the second scale degree. However, it should be noted that the lower boundary of this function is situated at roughly 119/108 above the Tonic, since notes located at smaller distances from the Tonic are liable to cause listeners to forget the ending pitch's relationship to the starting pitch- something which Supertonics don't do under any circumstances. Conspicuously, one type of Supertonic is the "'''Bidominant'''", which is the function specifically of [[9/8]]. | |||
=== Specific Types of Subvicinant === | |||
The four subtypes of Subvicinant are as follows... | |||
'''Subtonic''' - This subtype of Subvicinant is an interval that maps to both 6\7 and 20\24 in Bass-Up tonality and occurs above the Tonic as the seventh scale degree. However, it should be noted that the upper boundary of this function is situated at roughly 216/119 above the Tonic, since notes located at larger distances from the Tonic are liable to cause listeners to forget the ending pitch's relationship to the starting pitch- something which Subtonics don't do under any circumstances. Conspicuously, one type of Supertonic is the "'''Biserviant'''", which is the function specifically of [[16/9]]. | |||
'''Subaequient''' - This subtype of Subvicinant is an interval that maps to 6\7 and either 20\24 or 21\24 depending on a variety of factors. It is so named for the equable heptatonic region below the Tonic, which comprises the bulk of its range, and for its capacity to straddle the line between the Subtonic and Subabrogant functions in voice-leading. Conspicuously, it is distinct from Subtonic and Subabrogant functions only in finer tuning systems, with the approximation ranges for [[9/5]] and [[20/11]] being located at its borders. | |||
'''Subabrogant''' - This subtype of Subvicinant is not a traditional diatonic function at all since it is an interval that maps to both 6\7 and 21\24 in Bass-Up tonality. As per this function's name, the intervals in this range are like Subcollocants in that they may cause listeners to forget the ending pitch's relationship to the starting pitch in voice-leading. However, they, like Superabrogants, feel as if they're rather disconnected from the Tonic, and furthermore, the occurrence of two successive instances of these sorts of intervals in the same melodic line in the same direction is liable to come across as jarring. | |||
'''Subcollocant''' - This subtype of Subvicinant is the note typically referred to when people say "the leading tone", and an interval that usually maps to both 6\7 and 22\24 in Bass-Up tonality. Additionally, it has the Antiserviant function in Bass-Up tonality and the Antidominant function in Treble-Down tonality. Although triads built on this scale degree are regarded by some as simply incomplete Dominant Seventh chords, my own analysis, while acknowledging the functional similarities between the Subcollocant and the Dominant in Bass-Up tonality, sees this interval as functionally distinct from the Dominant due to the Subcollocant also being potentially related to the Mediant in the same way that the Dominant is related to the Tonic- a key functionality that is often exploited in [[Wikipedia:Vi–ii–V–I|circle progression]]s. In actuality, two subtypes of Subcollocant exist- the "'''Proximosubcollocant'''", which always maps to both 6\7 and 22\24 in Bass-Up tonality, and the "'''Distosubcollocant'''", which maps to 6\7 and either 21\24 or 22\24 depending on a variety of factors, and is distinct from both Proximosubcollocant and Subabrogant only in finer tuning systems where it is usually more consonant, and thus, weaker. An example of a Proximosubcollocant is [[243/128]] while an example of a Distosubcollocant is [[15/8]]. | |||
== Mediant and Contramediant Subtypes == | |||
There are five basic types of Mediant, although only three of them are distinct in [[24edo]]- you'd need to go to [[41edo]] or [[53edo]] to see all five. Similarly, there are five basic types of Contramediant, with only three of them being distinct in [[24edo]], so you'd need to go to [[41edo]] or [[53edo]] to see all five. | |||
=== Specific Types of Mediant === | |||
The five subtypes of Mediant are as follows... | |||
'''Proximomediant''' - This type of Mediant is mapped to 2\7 and 6\24 and is so named due to being located on the end of the Mediant range closest to the Tonic. Conspicuously, it is one of the possible the types of Mediant seen in Minor keys and is only distinct from the Mesoproximomediant in finer tuning systems where it is usually more dissonant. One subtype of Proximomediant is the "'''Triserviant'''", which is the function specifically of [[32/27]]. | |||
'''Mesoproximomediant''' - This type of Mediant is mapped to both 2\7 and either 6\24 or 7\24 depending on a variety of factors. It is so named due to being located between the proximal end of the Mediant range and the midline between the Tonic and the Dominant. Conspicuously, it is one of the possible the types of Mediant seen in Minor keys and is only distinct from the Proximomediant and Mesomediant in finer tuning systems where it's notable for containing the approximation range for [[6/5]] at its lower border and for being the [[fourth complement]] of the Superaequient, hence why it's not merely a simple compositing of the adjacent functions. | |||
'''Mesomediant''' - This type of Mediant is mapped to both 2\7 and 7\24 and is so named due to being located along the midline between the Tonic and the Dominant. This type of Mediant is arguably the most dissonant, and is not a traditional diatonic function at all, and in fact, it doesn't serve well at phrase endings- rather, its Tonic Parallel function is only appropriate during the middle of musical phrases. Intervals with this type of function include [[11/9]] and [[27/22]]. | |||
'''Mesodistomediant''' - This type of Mediant is mapped to both 2\7 and either 7\24 or 8\24 depending on a variety of factors. It is so named due to being located between the distal end of the Mediant range and the midline between the Tonic and the Dominant. Conspicuously, it is one of the possible the types of Mediant seen in Major keys and is only distinct from the Mesomediant and Distomediant in finer tuning systems where it's notable for containing the approximation range for [[5/4]] at its upper border and for being the fourth complement of the Distosupercollocant, hence why it's not merely a simple compositing of the adjacent functions. | |||
'''Distomediant''' - This type of Mediant is mapped to both 2\7 and 8\24 and is so named due to being located on the end of the Mediant range furthest from the Tonic. Conspicuously, it is one of the possible the types of Mediant seen in Major keys and is only distinct from the Mesodistomediant in finer tuning systems where it is usually more dissonant. One subtype of Distomediant is the "'''Quadridominant'''", which is the function specifically of [[81/64]]. | |||
=== Specific Types of Contramediant === | |||
The five subtypes of Contramediant are as follows... | |||
''' | '''Proximocontramediant''' - This type of Contramediant is mapped to 5\7 and 18\24 and is so named due to being located on the end of the Contramediant range closest to the Tonic. Conspicuously, it is one of the possible the types of Contraediant seen in Major keys and is only distinct from the Mesoproximocontramediant in finer tuning systems where it is usually more dissonant. One subtype of Proximocontramediant is the "'''Tridominant'''", which is the function specifically of [[27/16]]. | ||
''' | '''Mesoproximocontramediant''' - This type of Contramediant is mapped to 5\7 and either 17\24 or 18\24 depending on a variety of factors. It is so named due to being located between the proximal end of the Contramediant range and the midline between the Tonic and the Serviant. Conspicuously, it is one of the possible the types of Contramediant seen in Major keys and is only distinct from the Proximocontramediant and Mesocontramediant in finer tuning systems where it's notable for containing the approximation range for [[5/3]] at its upper border, hence why it's not merely a simple compositing of the adjacent functions. | ||
''' | '''Mesocontramediant''' - This type of Contramediant is mapped to both 5\7 and 17\24 and is so named due to being located along the midline between the Tonic and the Serviant. This type of Contramediant is arguably the most dissonant, and is not a traditional diatonic function at all, and in fact, it doesn't serve well at phrase endings- rather, its Tonic Parallel function is only appropriate during the middle of musical phrases. Intervals with this type of function include [[18/11]] and [[44/27]]. | ||
''' | '''Mesodistocontramediant''' - This type of Contramediant is mapped to both 5\7 and either 16\24 or 17\24 depending on a variety of factors. It is so named due to being located between the distal end of the Contramediant range and the midline between the Tonic and the Serviant. Conspicuously, it is one of the possible the types of Contramediant seen in Minor keys and is only distinct from the Mesocontramediant and Distocontramediant in finer tuning systems where it's notable for containing the approximation range for [[8/5]] at its lower border, hence why it's not merely a simple compositing of the adjacent functions. | ||
''' | '''Distocontramediant''' - This type of Contramediant is mapped to both 5\7 and 16\24 and is so named due to being located on the end of the Contramediant range furthest from the Tonic. Conspicuously, it is one of the possible the types of Contramediant seen in Minor keys and is only distinct from the Mesodistocontramediant in finer tuning systems where it is usually more dissonant. One subtype of Distomediant is the "'''Quadriserviant'''", which is the function specifically of [[128/81]]. | ||
== Antitonic == | == Antitonic Subtypes == | ||
Notes that occur around half an octave away from the Tonic | Notes that occur around half an octave away from the Tonic, on account of harmonies built on notes in this area tending to oppose that of the Tonic, are referred to by the term "Antitonic" by myself and others. It should be noted that the Antitonic is basically a first derivative function as it is derived from the Tonic through either perfect or imperfect Antipodism. In addition, the term "Antitonic" acts as a generic term for any of a group of diatonic functions found in this region. While some microtonal theorists insist that the Antitonic functionality is more fundamental than perhaps even the Dominant or Serviant, others, such as myself, disagree. | ||
=== Specific Types of Antitonic === | === Specific Types of Antitonic === | ||
The exact outcome and specific function of any given Antitonic depends on | The exact outcome and specific function of any given Antitonic depends on whether or not the interval in question is an augmented fourth or a diminished fifth. | ||
'''Sycophant''' - This type of Antitonic is mapped to both 3\7 and 12\24, and is named as such on account of it having a tendency to "kiss up to" and tonicize the Dominant- that is, to cause the Dominant to become a new Tonic- unless followed up by a different note such as some type of Mediant. A prototypical example of this type of Antitonic is 45/32. | |||
'''Tyrant''' - This type of Antitonic is mapped to both 4\7 and 12\24, and it tends to contrast with the Tonic in a manner somewhat akin to that of a Dominant, but by sheer brute force and contrary harmonic nature, and indeed these brute force Dominant-esque tendencies are the source of the name "Tyrant". For example, if the Tonic harmony is Minor in nature, the Antitonic harmony will be Major- or more rarely, Supermajor- in nature. Furthermore, in scales such as the Locrian scale, any type of Serviant harmony tends to resolve towards some other type of substitute for a Dominant, often bypassing this type of Antitonic, though on rare occasions, a Tyrant will act as a leading tone to the Serviant. A prototypical example of this type of Antitonic is 64/45. | |||
== Chromatic Functions == | |||
These functions are either derived through Adjacency relative to some First Derivative Diatonic function, or else, are derived from the Primary Diatonic functions through a Chromatic function-deriving operation. | |||
=== Primary Chromatic functions === | |||
The four basic Chromatic functions are as follows... | |||
'''Superdislocant''' - This is a note that is to the Supercollocant what a Tyrant is to a Sycophant. Specifically, it is the result of the Tonic being altered by some kind of chromatic semitone upwards and thus being displaced by a Nontonic function which leads away from the Tonic proper. | |||
'''Subdislocant''' - This is a note that is to the Subcollocant what a Tyrant is to a Sycophant. Specifically, it is the result of the Tonic being altered by some kind of chromatic semitone downwards and thus being displaced by a Nontonic function which leads away from the Tonic proper. | |||
'''Protosycophant''' - This is a note which can tonicize the Dominant, but because its harmonies fail to completely oppose those of the Tonic, it fails to count as a true Sycophant. A prototypical example of this type of interval is [[7/5]]. | |||
'''Prototyrant''' - This is a note which can tonicize the Serviant, but because its harmonies fail to completely oppose those of the Tonic, it fails to count as a true Tyrant. A prototypical example of this type of interval is [[10/7]]. | |||
=== Basic Chromatic Function-Deriving Operations === | |||
The way I see it, there are at least one known operation which can be used to derive additional Chromatic functions from various Diatonic functions. | |||
'''Displacement''' - This process results in a note that is near the Dominant or Serviant taking on similar functions to said notes rather than the opposite function, or, when applied to the Tonic, results in a Nontonic function that tends to want to lead away from the Tonic rather than towards it. This process is distinct from Detempering in that the notes created by this process are located at further distances from the note to which this process is applied. | |||
== Wolf Fifths, Wolf Fourths and the Uncanny Valleys of Harmony == | |||
As per Flora Canou's analysis<ref>''[[User:FloraC/Analysis on the 13-limit just intonation space: episode ii #Chapter V. Things Repel the Similar but Not Identical| Analysis on the 13-limit just intonation space: episode ii]]''. Flora Canou. Xenharmonic Wiki.</ref>, there are uncanny valleys on either side of each of the three primary functions. In this analysis, she states the following: | |||
<div style="font-style: italic; border: 1px solid silver; margin: 15px; padding: 15px;"> | |||
: From a historical perspective, meantone was discovered for a good reason. Letting it do its duty is of the greatest mercy. Not accounting for the discordance of wolf fifths or melodic bumps is equivalent to holding that meantone need not exist, and that most recent to modern theories are either failure or flukes based on wrong principles. | |||
</div> | |||
However, my contention is that while meantone doing its duty around the Tonic makes sense as [[81/80]] is really quite discordant, it seems that under certain circumstances, the average listener acquainted with [[12edo]] music will not notice wolf fourths or wolf fifths unless they are explicitly pointed out, thus not only are there other methods of accounting for the discordance of wolf fourths and wolf fifths besides shunning them, but there are additional functions hiding in the shadows of the three primary functions, along with rules governing their usage, which shall be covered in this section. | |||
=== Circumtonic Regions === | |||
The Circumtonic regions are the two main regions on either side of the Tonic, outside the Tonic's "event horizon". These intervals are invariably inside the Tonic's uncanny valleys, and the uncanny valleys around the Tonic, unlike those around the other two functions, are very deep, and as a result, wolf intervals around the Tonic are tolerable in ornamentation but not melody or harmony. Thus, these intervals cannot be directly approached from the Tonic, even melodically, and so they're usually avoided outside of modulation. | |||
'''Supercommatic''' - This is a note that occurs at intervals from about 3.5 cents to roughly 25 cents above the Tonic. These intervals are little more than stepping stones in modulation, and extra intervals that can be used together with the Tonic for a sense of dissonance, or for a slightly less resolved version of a Unison or Octave. | |||
'''Subcommatic''' - This is a note that occurs at intervals from about 3.5 cents to roughly 25 cents below the Tonic. As with Supercommatic intervals, these intervals are little more than stepping stones in modulation, and extra intervals that can be used together with the Tonic for a sense of dissonance. | |||
=== Circumdominant Regions === | |||
The circumdomimant regions are the two main regions on either side of the Dominant proper, and since the uncanny valleys around the Dominant are not as deep as those around the Tonic, there is more room for actual first derivative diatonic functionality, as well as other functionalities. Note that together with the Dominant itself, these functions are collectively called "'''Protodominants'''", as there are many systems where what would be the Dominant fails to get distinguished from either one or the other of the functions listed here. | |||
'''Geminodominant''' - This is a note that occurs roughly at intervals ranging from about 3.5 cents beyond [[22/15]] to about 3.5 cents short of the 3/2 perfect fifth in the scale's direction of construction. Although often overlooked or even outright shunned by traditional theorists, the Geminodominant is a legitimate diatonic function in terms of this analysis- albeit one only existing in non-meantone environments in which it is easily derived from the Dominant through detempering, occurring in [[5-limit]] diatonic environments, and acting as a sort of "fraternal twin" to the Dominant, hence its name. Specifically, as typified by intervals like [[40/27]], Geminodominants are dissonant intervals that simultaneously act as alternatives to the Dominant in both chord progressions and chord construction, and often require resolution, though they also have a Preserviant function. The dissonance of this function relative to a chord root is useful in preventing tonicization of chords built on the traditional weak harmonies- the Mediant and the Contramediant- which also has the benefits of strengthening interrupted cadences and creating the sense of impending movement, but outside of these usages and well supported chords, this kind of thing is best avoided since things repel the similar but not identical. Apart from diatonic contexts, Geminodominants only rise to prominence in systems where what might otherwise function as a Dominant is found just short of the sweet spot range near the standard issue 3/2. | |||
'''Pseudodominant''' - This is a note that occurs roughly at intervals ranging from about 3.5 cents to about 25 cents beyond the 3/2 perfect fifth in the scale's direction of construction. Because none of these intervals arise naturally in a [[5-limit]] diatonic scale, and because they fall within one of the Dominant's uncanny valleys, it is rare to see this functionality outside of systems where what might otherwise function as a Dominant is found just beyond the sweet spot range near the standard issue 3/2. However, these intervals naturally arise in the Circle of Thirteenth Harmonics, in which case they have a Predominant function. | |||
=== Circumserviant Regions === | |||
The circumserviant regions are the two main regions on either side of the Serviant proper, and since the uncanny valleys around the Dominant are not as deep as those around the Tonic, there is more room for actual first derivative diatonic functionality, as well as other functionalities. Note that together with the Serviant itself, these functions are collectively called "'''Protoserviants'''", as there are many systems where what would be the Serviant fails to get distinguished from either one or the other of the functions listed here. | |||
'''Geminoserviant''' - This is a note that occurs roughly at intervals ranging from about 3.5 cents beyond the 4/3 perfect fourth to about 3.5 cents short of [[15/11]] in the scale's direction of construction. Although often overlooked or even outright shunned by traditional theorists, the Geminodominant is a legitimate diatonic function in terms of this analysis- albeit one only existing in non-meantone environments in which it is easily derived from the Serviant through detempering, occurring in 5-limit diatonic environments, and acting as a sort of "fraternal twin" to the Serviant, hence its name. As typified by intervals like [[27/20]], Geminoserviants are dissonant intervals that often act as a sort of Predominant and or as the inverses of Geminodominants. The dissonance of this function relative to a chord root is useful in preventing tonicization of chords built on the Mediant and the Contramediant, but outside of these usages and well supported chords, this kind of thing is best avoided. Apart from diatonic contexts, Geminoserviants only rise to prominence in systems where what might otherwise function as a Serviant is found just beyond the sweet spot range near the standard issue 4/3. | |||
'''Pseudoserviant''' - This is a note that occurs roughly at intervals ranging from about 25 cents to about 3.5 cents short of the 4/3 perfect fourth in the scale's direction of construction. Because none of these intervals arise naturally in a [[5-limit]] diatonic scale, and because they fall within one of the Serviant's uncanny valleys, it is rare to see this functionality outside of systems where what might otherwise function as a Serviant is found just short the sweet spot range near the standard issue 4/3. However, these intervals naturally arise in the Circle of Thirteenth Harmonics, in which case they have a Preserviant function. | |||
=== Governing Rules === | |||
'''Commatic Repulsion''' - This rule is best summed up in Flora Canou's statement that things repel the similar but not identical. To illustrate this principle, let's take a look at the VImin chord as is present in [[meantone]] and contrast it to the situation outside of meantone. Believe it or not, the meantone VImin chord has no fewer than two separate functions relative to the Tonic. First of all, there's the Relative Minor functionality, which is 5/3–1/1–5/4 relative to the Tonic and can tonicize as a new Imin either temporarily, as in a deceptive cadence, or permanently as in a modulation. Secondly, there's the Tertiary Dominant functionality, which is 27/16-81/80-81/64 relative to the Tonic and, as the name suggests, acts as the Dominant of the Dominant's own Dominant. While both of these are fused together in meantone, these two functions are separated exactly by the syntonic comma in non-meantone environments, and the only way to use a VImin chord with both functions is to temper out the syntonic comma. As Flora Canou has stated: | |||
<div style="font-style: italic; border: 1px solid silver; margin: 15px; padding: 15px;"> | |||
: If the comma is not tempered out, the progression does not hold. The idea to force it is absurd. Fitting one function will leave the other emergent function[s] misplaced by a comma, which is easily the most catastrophic scene [musically] – the uncanny valley of harmony. | |||
</div> | |||
However, in non-meantone settings, it is possible to have a chord which shares its root with the Tertiary Dominant and shares both its third and fifth with the Relative Minor. Since such an arrangement results in a wolf fifth, and since the wolf fifth is a dissonance requiring resolution, one could argue that such a chord has a function distinct from the more traditional options- specifically one which is involved in interrupted cadences, as well as in starting cadences that "wind down" such as VImin-IVmaj-Imaj or even VImin-Vmaj-Imaj. This particular function is what I call the ''Major Contramediant Tensive''. | |||
'''Primary Adpositive Purity''' - This rule is that for every chord root located one step away from either the Tonic, Dominant or Serviant along the Circle of Fifths, there is a demand for the fifth of the chord in question to be within 3.5 cents of a just 3/2, though in the case of a chord that has a root located at two steps away from the Tonic along the along the Circle of Fifths, the fifth of the chord can be deliberately subjected to the process of Displacement as mentioned before and not run afoul of this restriction. However, chord roots that are located three or more steps away from the Tonic along the circle of fifths are not subject to the aforementioned restriction due to their distance. This means that the Tonic, Dominant, Serviant, Supertonic and Subtonic chords all demand a perfect fifth as the fifth of the chord, whether you are building the Tonality upwards or downwards, but wolf fifths can occur easily as the fifth of chords which are located three or more steps away from the Tonic. | |||
== | == Beyond Diatonic and Chromatic Functional Harmony == | ||
In addition to all the aforementioned Diatonic functions, there is an additional set of categories for dealing with the notes in between the various Diatonic scale degrees. | In addition to all the aforementioned Diatonic and Chromatic functions, as well as the detemperings of diatonic functions, there is an additional set of categories for dealing with the notes in between the various Diatonic scale degrees. | ||
=== History === | === History === | ||
I've been in the process of developing this since well before I officially joined the Microtonal community, in fact, it all started for me with my discovery of the nature of the eleventh harmonic as a quartertone, however, while it is only thanks to a YouTuber who goes by "Quartertone Harmony" <ref>[https://www.youtube.com/channel/UCeDhhWQYqGRPy5ES8gTtIAQ Quartertone Harmony - YouTube]</ref> that I've been able to fill in significant gaps in my theory, the reality is that the idea of extending Diatonic functional harmony to cover intervals between the standard scale degrees, can trace at least some of its roots back to the work of [[Ivan Wyschnegradsky]]. | |||
[[File: | Specifically, idea of extending Diatonic functional harmony to cover intervals between the standard scale degrees- an idea that has at least some roots in Wyschnegradsky's concept of [[Wikipedia: Major fourth and minor fifth|"Major Fourth" and "Minor Fifth"]]. However, I wanted to use LCJI as a basis for defining these intervals and thus decided to take [[11/8]] as being the just version of Wyschnegradsky's "Major Fourth", and while I drew up sketches based loosely on [[24edo]] for early versions of this concept, I also realized that that two instances of [[33/32]] added up to an interval smaller than [[2187/2048]] but which had a similar function. Furthermore, since two instances of 11/8 resulted in an interval in the vicinity of a Major seventh, I decided to take stacks of 11/8 to form a second navigational axis which works together with the Diatonic Axis in order to define the microtonal functions positioned roughly halfway between the German and Viennese Diatonic functions, though there are a few other microtonal functions as well that are not immediately covered by this second axis. | ||
[[File:Diatonic Function Map.png|thumb|Initial diagram of paradiatonic function locations I made around the time of officially joining the Xenharmonic community. Note that a number of the functions listed on this page are missing, while the Supercollocant, the Superabrogant, the Subabrogant, the Intersubiant, the Interregnant, the Superobstant and the Subobstant initially had different names.]] | |||
Most traditional music theorists know that there are basically two types of semitones- the diatonic semitone or minor second, and the chromatic semitone or augmented prime. They also know that a diatonic semitone and a chromatic semitone add up to a whole tone. The same things are true in Just Intonation as well as in EDOs other than 12edo or even 24edo. In [[Talk:159edo notation #My Second Idea for a Notation System|a conversation]] between myself and [[Kite Giedraitis]] about this topic, Kite mentioned that there are two types of semitone in 3-limit tuning- a diatonic semitone of with a ratio of 256/243, and the aforementioned 2187/2048- a chromatic semitone that is otherwise known as the Apotome- which, when added together, add up to a 9/8 whole tone. Furthermore, Kite also mentioned how in 5-limit tuning, these same semitones exist alongside other semitones derived through alteration by [[81/80]]. On one hand, adding 81/80 to 256/243 yields 16/15, and adding another 81/80 yields [[27/25]]- two additional diatonic semitones. On the other hand, subtracting 81/80 from the Apotome yields [[135/128]], and subtracting another 81/80 yields 25/24- two additional chromatic semitones. When added up in the proper pairs- 16/15 with 135/128, and 27/25 with 25/24- the additional sets of semitones again yield a 9/8 whole tone. In light of all this, Kite argued that the familiar sharp signs and flat signs- which are used to denote the chromatic semitone- were never meant to denote exactly half of a whole tone, but rather, a whole tone minus a minor second. | Most traditional music theorists know that there are basically two types of semitones- the diatonic semitone or minor second, and the chromatic semitone or augmented prime. They also know that a diatonic semitone and a chromatic semitone add up to a whole tone. The same things are true in Just Intonation as well as in EDOs other than 12edo or even 24edo. In [[Talk:159edo notation #My Second Idea for a Notation System|a conversation]] between myself and [[Kite Giedraitis]] about this topic, Kite mentioned that there are two types of semitone in 3-limit tuning- a diatonic semitone of with a ratio of 256/243, and the aforementioned 2187/2048- a chromatic semitone that is otherwise known as the Apotome- which, when added together, add up to a 9/8 whole tone. Furthermore, Kite also mentioned how in 5-limit tuning, these same semitones exist alongside other semitones derived through alteration by [[81/80]]. On one hand, adding 81/80 to 256/243 yields 16/15, and adding another 81/80 yields [[27/25]]- two additional diatonic semitones. On the other hand, subtracting 81/80 from the Apotome yields [[135/128]], and subtracting another 81/80 yields 25/24- two additional chromatic semitones. When added up in the proper pairs- 16/15 with 135/128, and 27/25 with 25/24- the additional sets of semitones again yield a 9/8 whole tone. In light of all this, Kite argued that the familiar sharp signs and flat signs- which are used to denote the chromatic semitone- were never meant to denote exactly half of a whole tone, but rather, a whole tone minus a minor second. | ||
Building on Kite's logic, I then decided to apply similar distinctions among quartertones, and thus make the argument that quartertones don't have to denote exactly one fourth of a whole tone in as of themselves, but rather, they only have to add up to a whole tone when paired up correctly. However, the catch was that for quartertones, there are sometimes multiple correct options, making things more complicated. I decided to define the musical functions of quartertones initially on an informal basis by drawing a distinction between the terms "'''Parachromatic'''" (from the prefix ''para-'' in both the senses of ''alongside'' and ''resembling''<ref>[[Wiktionary: para- #Etymology 1]]</ref>, and the word ''chromatic'') and "'''Paradiatonic'''" (from the same two senses of the prefix ''para-'' and the word ''diatonic'') for purposes of classifying quartertone intervals. This was easy, since | Building on Kite's logic, I then decided to apply similar distinctions among quartertones, and thus make the argument that quartertones don't have to denote exactly one fourth of a whole tone in as of themselves, but rather, they only have to add up to a whole tone when paired up correctly. However, the catch was that for quartertones, there are sometimes multiple correct options, making things more complicated. I decided to define the musical functions of quartertones initially on an informal basis by drawing a distinction between the terms "'''Parachromatic'''" (from the prefix ''para-'' in both the senses of ''alongside'' and ''resembling''<ref>[[Wiktionary: para- #Etymology 1]]</ref>, and the word ''chromatic'') and "'''Paradiatonic'''" (from the same two senses of the prefix ''para-'' and the word ''diatonic'') for purposes of classifying quartertone intervals. This was easy, since I had found that two instances of 33/32 added up to [[1089/1024]] rather than 2187/2048, and, since I had informally added the "para-" prefix (in the same senses) to both "Major" and "Minor" to create the terms '''Paramajor''' and '''Paraminor''' to better describe how 11/8 and 16/11 related to 128/99 and 99/64 respectively in order to describe how, for instance, the notes at 99/64 and 16/11 above the Tonic relate to each other in much the same way as major and minor intervals do, except that this relationship occurs in a context where the note halfway between them is actually part of the base scale rather than the two notes in question, and there's a different interval between said two notes than the base scale's chroma. | ||
The way I see it, paradiatonic quartertones are analogous to diatonic semitones in that they are denoted as seconds, albeit inframinor seconds by default, while parachromatic quartertones are analogous to chromatic semitones in that they are denoted as primes, albiet as ultraprimes by default. However, the distinction goes further than that- a parachromatic quartertone and a paradiatonic quartertone add up to a diatonic semitone, while two parachromatic quartertones add up to a chromatic semitone. Given both these definitions for "paradiatonic" and "parachromatic", and given that a diatonic semitone and a chromatic semitone add up to a whole tone when paired correctly, it can be deduced that a whole tone can be assembled from three parachromatic quartertones and one paradiatonic quartertone. Because there are sometimes multiple correct options for assembling parachromatic and paradiatonic intervals to make a 9/8 whole tone, I ended up choosing the simplest configuration of paradiatonic and parachromatic intervals to assemble in order to create a 9/8 whole tone- a configuration that only requires one type of parachromatic quartertone and one type of paradiatonic quartertone. As a result of multiple factors, I ended up choosing the combination of three 33/32 parachromatic quartertones and one [[4096/3993]] paradiatonic quartertone as the JI basis for this in regards to both Diatonic theory and [[Alpharabian tuning]], and, through interactions with others in the Xenharmonic community, I was later influenced by others on Discord to take [[MOS]]-based structural considerations into account. This eventually resulted in the first formal definition of a "'''parachroma'''" (an interval that can be easily tempered to equal half of a MOS-chroma), and later, the "'''parastep'''" (the interval that remains after subtracting as many parachromas from a Major MOS-step as possible without resulting in a negative interval). Finally, drawing from the concept of "parachromas" as applied to MOS-based contexts, I was able to finally give a formal definition of terms like "paramajor" (the result of adding a parachroma to either a MOS generator or its period-inverse) and "paraminor" (the result of subtracting a parachroma from a MOS generator or its period-inverse), which I had previously come up with on an informal basis. | The way I see it, paradiatonic quartertones are analogous to diatonic semitones in that they are denoted as seconds, albeit inframinor seconds by default, while parachromatic quartertones are analogous to chromatic semitones in that they are denoted as primes, albiet as ultraprimes by default. However, the distinction goes further than that- a parachromatic quartertone and a paradiatonic quartertone add up to a diatonic semitone, while two parachromatic quartertones add up to a chromatic semitone. Given both these definitions for "paradiatonic" and "parachromatic", and given that a diatonic semitone and a chromatic semitone add up to a whole tone when paired correctly, it can be deduced that a whole tone can be assembled from three parachromatic quartertones and one paradiatonic quartertone. Because there are sometimes multiple correct options for assembling parachromatic and paradiatonic intervals to make a 9/8 whole tone, I ended up choosing the simplest configuration of paradiatonic and parachromatic intervals to assemble in order to create a 9/8 whole tone- a configuration that only requires one type of parachromatic quartertone and one type of paradiatonic quartertone. As a result of multiple factors, I ended up choosing the combination of three 33/32 parachromatic quartertones and one [[4096/3993]] paradiatonic quartertone as the JI basis for this in regards to both Diatonic theory and [[Alpharabian tuning]], and, through interactions with others in the Xenharmonic community, I was later influenced by others on Discord to take [[MOS]]-based structural considerations into account. This eventually resulted in the first formal definition of a "'''parachroma'''" (an interval that can be easily tempered to equal half of a MOS-chroma), and later, the "'''parastep'''" (the interval that remains after subtracting as many parachromas from a Major MOS-step as possible without resulting in a negative interval). Finally, drawing from the concept of "parachromas" as applied to MOS-based contexts, I was able to finally give a formal definition of terms like "paramajor" (the result of adding a parachroma to either a MOS generator or its period-inverse) and "paraminor" (the result of subtracting a parachroma from a MOS generator or its period-inverse), which I had previously come up with on an informal basis. | ||
=== | == The Realm of the Paradiatonic and the Parachormatic == | ||
In January of 2022, Quartertone Harmony posted a video in which he grouped together a series of functions he refered to in the video as the "shadow scale"<ref>[https://www.youtube.com/watch?v=P6WJryxB_0Y Quartertone Harmony - Harmonic Functions of Quartertones SD 480p]</ref>, which I will refer to here as a '''paradiatonic scale''' since there are technically two of these, and this in turn led to the separation of Paradiatonic and Parachromatic harmonic functions for me. This whole concept of a "shadow scale", in addition to everything else discuss in this section, paves the way for my idea of [[MOS-Shadow theory]], but, aside from how it applies to Diatonic-scale based functional harmony, MOS-Shadow theory is another whole discussion for another time. | |||
=== The Paradiatonic Scales === | |||
The Paradiatonic scales from a given tonic acts as a sort of "second shelf" of that tonality. Note that scale degrees in parentheses are optional. | |||
The '''Bright Paradiatonic Scale''' consists of the following scale degrees as analyzed relative to Viennese Theory's scale steps: | |||
I, tII/dbIII, (dIII), tIV, dV, (dVI), tVI/dbVII, tVII | |||
''' | The '''Dark Paradiatonic Scale''' consists of the following scale degrees as analyzed relative to Viennese Theory's scale steps: | ||
I, dbII tII/dbIII, (dIII), tIV, dV, (dVI), tVI/dbVII | |||
While the Diatonic scale itself has seven notes, the two Paradiatonic scales each have eight notes, furthermore, the tunings of each note in each Paradiatonic scale not only depend upon the exact tuning of the Diatonic scale used as a basis, but also vary considerably when it comes to the notes of the Paradiatonic that occur between the main Diatonic interval category ranges. | |||
=== Basic Paradiatonic Functions === | |||
Out of the various functions found in the Paradiatonic scales, four of them- specifically, the tII/dbIII, tIV, dV and tVI/dbVII- can be considered basic, while the other three are first derivatives. As with the three basic diatonic functions, the four most basic paradiatonic functions have their roots in LCJI. In the order listed, the tII/dbIII, tIV, dV and tVI/dbVII functions are the following... | |||
'''Contravaricant''' - | '''Contravaricant''' - Named in contrast to the Varicant function, this is an interval that maps to both 1\5 and 5\24 in the scale's direction of construction, lying roughly in the middle of the 4/3 interval separating the Tonic and the Serviant above it. Intervals in the Contravaricant region often don't consistently act as either seconds or thirds, or even act as a cross between a second and a third, only without potential for crowding in chords. In Bass-Up tonality, this functionality is first encountered in the form of [[8/7]], though [[7/6]] is another notable interval included in this range, with intervals in this range having Predominant, Preserviant, and Dominant Parallel functions, as well as an overlap between Tonic Adjacent and Tonic Parallel functions. There are two different subtypes of this function that differ from each other based on how they are approached in interval stacking, the "'''Pseudobidominant'''", which arises from stacking two Pseudodominants, and the "'''Pseudotriserviant'''", which arises from stacking three Pseudoserviants. | ||
''' | '''Intersubiant''' - This is an interval that maps to both 3\7 and 11\24 in the scale's direction of construction and comprises the intervals ranging from around 3.5 cents short of [[15/11]] to around 3.5 cents beyond [[11/8]]. Like both the Serviant and the Sycophant, intervals in this region have a Predominant function, however, this predominant function is weaker than that of the surrounding interval regions since they neither act as a counterweight to the Dominant like a Serviant nor do they completely tonicize the Dominant like a Sycophant- at least to those who are more familiar with quartertones. What is even less expected is that these same intervals also have Preserviant and Mocktyrant functions. Since the Intersubiant is not found in the Tonic's quartertone field, there is a tendency for Intersubiant chords to be preceded and or followed by other chords with roots in the same quartertone field, though one could also reasonably approach it from the Tonic, the Serviant, some kind of Contramediant, some kind of Supervicinant, or, in some tuning systems, certain kinds of Mediant. In Bass-Up tonality, this functionality has its roots in the eleventh harmonic. | ||
''' | '''Interregnant''' - This is an interval that maps to both 4\7 and 13\24 in the scale's direction of construction and comprises the intervals ranging from around 3.5 cents short of [[16/11]] to around 3.5 cents beyond [[22/15]]. Accordingly, intervals in this region behave as a cross between a Tyrant Antitonic on one hand and a Dominant on the other in that they often contrast with the Tonic through some combination of harmonic connection and brute force contrast, though it unexpectedly has decent Predominant and Mocksycophant functions. Like the Intersubiant, the Interregnant is not found in the Tonic's quartertone field and is either very distant from the Tonic along the circle of fifths or is completely missed by said circle of fifths, thus, there is a tendency for Interregnant chords to be preceded and or followed by other chords with roots in the same quartertone field. Conspicuously, the distance between the Interregnant is only about a Minor Second- or, at the very most, a Supraminor Second- away from the Intersubiant, so as a result, the Interregnant can be both a set-up and a follow-up to the Intersubiant. In Bass-Up tonality, the Interregnant functionality has its roots in the eleventh subharmonic. | ||
'''Varicant''' - Just as a Mediant lies roughly in the middle of the 3/2 interval separating the Tonic and the Dominant above it, a Varicant lies roughly in the middle of the 4/3 interval separating the Dominant and the Tonic above it. Intervals in this region often don’t consistently act as either sixths or sevenths, or even act as a cross between a sixth and a seventh, only without potential for crowding in chords- effectively straddling the border between these two diatonic categories, hence the name "Varicant", from Latin "vāricō"<ref>[[Wiktionary: varico #Latin]]</ref>. This is an interval that maps to both 4\5 and 19\24 in the scale's direction of construction. In Bass-Up Tonality, this functionality is first encountered in the form of the [[7/4]] interval, though [[12/7]] is another notable interval included in this range. While many microtonalists think of 7/4 as being purely a type of seventh- and indeed, it most commonly acts as a sort of subminor seventh- I counterargue based on this same interval's relationships with 11/8 in particular that 7/4 is not merely a type of seventh, but rather, a type of a cross between a sixth and a seventh, with such a property explaining why [[14/11]] is generally considered to be a type of third. Furthermore, in contrast to the Subtonics of Bass-Up Tonality, Varicants are liable to act as Predominants, Preserviants, and Serviant Parallels, as well as display an overlap between Tonic Adjacent and Tonic Parallel functions. There are two different subtypes of this function that differ from each other based on how they are approached in interval stacking, the "'''Pseudotridominant'''", which arises from stacking three Pseudodominants, and the "'''Pseudobiserviant'''", which arises from stacking two Pseudoserviants. | |||
=== Derivative Paradiatonic Functions === | |||
''' | '''Subgradient''' - This is a note that occurs at intervals between roughly 48/25 above the Tonic and roughly 25 cents below the octave reduplication of the Tonic. These intervals tend to act as parachromatic alterations of either the Tonic, or, more rarely in Bass-Up Tonality, the Subcollocant- however, there are functional differences between a Subgradient and a Subcollocant in Bass-Up Tonality. In Bass-Up Tonality, Subgradients are often more likely to be passing tones than Subcollocants, and, when they’re not merely passing non-chord tones, they are often harder to approach and or follow up without creating some kind of awkward tonal disconnect, with such a disconnect being especially noticeable for intervals like [[64/33]]. Furthermore, whereas a Lead can resolve to the Tonic in part through a strong harmonic connection, a Subgradient is much more likely to do so through sheer brute force, and even these cases require a proper set-up, as otherwise, the awkward tonal disconnect between the Subgradient and the Tonic is likely to result in the Subgradient resolving back down to either the Subcollocant or the Subabrogant. As if that weren't enough, the Subgradient also has the Antintersubiant function. This function used to be called the "Subdietic", though that term has since been restricted to a related composite function (see below on Composite Functions). | ||
''' | '''Supergradient''' - This is a note that occurs at intervals between roughly 25 cents above the Tonic and 25/24 above the Tonic. These intervals tend to act as parachromatic alterations of either the Tonic, or, more rarely in Bass-Up Tonality, the Supercollocant. However, there are a few functional differences between a Supergradient and a Supercollocant in Bass-Up Tonality that are worth considering. For starters, Supergradients are often more likely to be passing tones than Supercollocants, and, when they’re not merely passing non-chord tones, they are just as liable to resolve upward through some sort of semitone-like motion to some form of Supercollocant or Superabrogant, as they are to resolve downwards toward the Tonic, a property which intervals like 33/32 in particular are apt to demonstrate. Furthermore, whereas a Supercollocant can resolve to the Tonic in part through a strong harmonic connection, a Supergradient is much more likely to do so through sheer brute force when such a resolution is noticeable. As if that weren't enough, the Subgradient also has the Antinterregnant function. This function used to be called the "Superdietic", though that term has since been restricted to a related composite function (see below on Composite Functions). | ||
=== | === Parachromatic Functions === | ||
These are quartertone functions that are not on the Paradiatonic Scale. Of these, there are only two basic functions... | |||
''' | '''Superobstant''' - This is a note which, in Bass-Up tonality, is mapped to 9\24. This region is characterized by intervals that don’t consistently act as either thirds or fourths, or even act as a cross between a third and a fourth, as well as by intervals that act as parachromatic alterations of either the Mediant or the Serviant. As per the name, which comes from "super-" and "obstant", the latter of which comes from Latin "obstō"<ref>[[Wiktionary: obsto #Latin]]</ref>, intervals in this region are also generally more dissonant and have a tendency to disrupt both chords and melodies, leading to their avoidance in chords outside of deliberate dissonances. Chords of this type have Preserviant, Preintersubiant and Preinterregnant functions as well as Premediant functions. | ||
''' | '''Subobstant''' - This is a note which, in Bass-Up tonality, is mapped to 15\24. This region is characterized by intervals that don’t consistently act as either fifths or sixths, or even act as a cross between a fifth and a sixth, as well as by intervals that act as parachromatic alterations of either the Dominant or the Contramediant. As per the name, which comes from "sub-" and "obstant", which, as mentioned before, comes from Latin "obstō", intervals in this region are also generally more dissonant, leading to their avoidance in chords outside of deliberate dissonances. Chords of this type have Predominant, Preintersubiant and Preinterregnant functions, as well as Precontramediant functions, and, perhaps very tellingly, tend to utilize Diminished Fourths instead of Major Thirds due to the functions of the Subgradient- which usually gets incorporated into these kinds of chords. | ||
== Diatonic, Paradiatonic, and the Tonic's Proximal Pythagorean Aura == | |||
''' | One of the things that Quartertone Harmony has found and mentioned<ref>[https://www.youtube.com/watch?v=3N_l5ciE14g Quartertone Harmony - The Truth About Quartertone Melodies]</ref> is that when dealing with quartertones, there seems to be something about a given 12-tone scale in 24edo which assures that notes in that same field will sound like they go together. However, in systems such as 159edo, you begin to see that things are slightly more complicated, as this distinctive atmosphere or quality turns out to be around 20 cents at widest and seems to surround and be generated by notes related to the Tonic by Pythagorean intervals that aren't all that far away from the Tonic, hence the term '''proximal Pythagorean aura''' to refer to it. Notably, the proximal Pythagorean aura is at its thickest at around six or seven steps away from the Tonic in either direction along the circle of fifths, and extends along the circle of fifths on either side of these areas from two steps away from the Tonic to eleven steps away from the Tonic. The presence of this aura explains things related to the uncanny valleys around the Dominant and Serviant- namely why these uncanny valleys are not as deep or as wide as those around the Tonic, and why simple intervals with single factors of prime 5 seem to be at least somewhat "in key" relative to the Tonic. It should be noted that the Tonic, the Dominant, and the Serviant work together with this aura to define safe regions for field shifts that are guaranteed to not come across as jarring. Intervals outside of this aura, such as most paradiatonic intervals, must abide by certain rules in order to not come across as jarring. | ||
== Additional Functions == | == Additional Composite Functions == | ||
Notes on the boundaries of functional regions have multiple functions due to occurring at the boundary between different functions, the process by which this happens is known as '''Compositing'''. As for the actual composite functions themselves, there are quite a few of them. | |||
'''Subdietic''' - This function is a compositing of Subcommatic and Subgradient, and as Subcommatic is part of its nature, it is effectively repelled harmonically. It should be noted that this is one of only a handful of composite functions which are formed by the overlap between different functional regions rather than merely being located at a boundary. | |||
'''Superdietic''' - This function is a compositing of Supercommatic and Supergradient, and as Supercommatic is part of its nature, it is effectively repelled harmonically. It should be noted that this is one of only a handful of composite functions which are formed by the overlap between different functional regions rather than merely being located at a boundary. | |||
''' | '''Subsanguinant''' - This function is one of two "bleeding tone" functions- hence its Latin-derived name- and is a compositing of Subgradient and Proximosubcollocant functions, and thus, has a more tense feel than a Proximosubcollocant alone. It should be noted that this function is formed by the overlap between different functional regions rather than merely being located at a boundary. | ||
''' | '''Supersanguinant''' - This function is one of two "bleeding tone" functions- hence its Latin-derived name- and is a compositing of Supergradient and Proximosupercollocant functions, and thus, has a more tense feel than a Proximosupercollocant alone. It should be noted that this function is formed by the overlap between different functional regions rather than merely being located at a boundary. | ||
''' | '''Submaculant''' - This function is a compositing of Subgradient and Subdislocant, and thus is like the chromatic version of the Subsanguinant. | ||
''' | '''Supermaculant''' - This function is a compositing of Supergradient and Superdislocant, and thus is like the chromatic version of the Supersanguinant. | ||
''' | '''Acuotyrant''' - This function is a compositing of Prototyrant and Interregnant in Bass-Up Tonality, and although an interval like this generally fails to truly oppose the harmonies of the Tonic, it nevertheless operates more on the side of brute force when it contrasts with the Tonic. | ||
'''Gravosycophant''' - This function is a compositing of Protosycophant and Intersubiant in Bass-Up Tonality, and although an interval like this generally fails to truly oppose the harmonies of the Tonic, it nevertheless often runs a high risk of tonicizing the Geminodominant. | |||
'''Gravotyrant''' this function is a compositing of Prototyrant and Interregnant in Treble-Down Tonality, and although an interval like this generally fails to truly oppose the harmonies of the Tonic, it nevertheless operates more on the side of brute force when it contrasts with the Tonic. | |||
''' | '''Acuosycophant''' - This function is a compositing of Protosycophant and Intersubiant in Treble-Down Tonality, and although an interval like this generally fails to truly oppose the harmonies of the Tonic, it nevertheless often runs a high risk of tonicizing the Geminodominant. | ||
== Extra Functions of Prime Harmonics and Subharmonics == | |||
It should be noted that there are other layers of function besides those oriented around the [[3-limit]]. These are detailed here. | |||
''' | '''Paradominant''' - This function typically appears along prime axes other than that of the 3-limit in which they take Dominant-like function. Thus, for example, in Bass-Up Tonality, the note at 5/4 above the Tonic, being a direct prime harmonic of the Tonic, gets to serve this function in addition to its Mesodistomediant function as defined by the 3-limit, with the Paradominant function emerging mainly in a series of 5/4-based motions leading to the Tonic. When considered alongside the actual Dominant function of 3/2, however, Paradominants take on the function of Predominant owing to the fact that the Dominant function of 3/2 is actually stronger than that of any predominant due to being closer to the fundamental. | ||
''' | '''Paraserviant''' - This function is essentially the inverse of the Paradominant function, and acts as a sort of counterweight to the Paradominant relative to the Tonic. Like the Paradominant function, it typically appears along prime axes other than that of the 3-limit in which they take Serviant-like function. Thus, for example, in Bass-Up tonality, the note at 8/5 above the Tonic, being a direct prime subharmonic of the Tonic, gets to serve this function in addition to its Mesodistocontramediant function as defined by the 3-limit. When considered alongside the actual Serviant function of 4/3, however, Paraserviants take on the function of Preserviant since the Serviant function of 4/3 is stronger. | ||
== References == | == References == | ||
| Line 151: | Line 307: | ||
[[Category:Terms]] | [[Category:Terms]] | ||
[[Category: | [[Category:Harmony]] | ||
[[Category:Method]] | [[Category:Method]] | ||
[[Category:Diatonic]] | [[Category:Diatonic]] | ||
Latest revision as of 19:57, 17 May 2025
One construct from Western Classical music with potential implications for Microtonalists is harmonic function- especially as it pertains to the diatonic MOS scale and its various relatives. In Mainstream Music Theory there were once two prevailing schools of thought in regards to diatonic functional harmony- German Theory and Viennese Theory- however, in a conversation with Mousemambo on Discord, it has been revealed to me that in modern practice, the old ideas of functional harmony have largely disintegrated due firstly to the conviction that after around 1900 CE, art music took a turn away from Common Practice Period foundations and those old analyses just don't work anymore as originally formulated, and secondly due to a suspicion that they never really existed beyond the pareidolia of minds trying to see patterns in noise. Mousemambo has also pointed out to me that modern writers have moved away from the convoluted depths of the two Germanic schools, now more often simply identifying scale degrees and the chords for which they are the root as either Tonic; Dominant, which is basically anything leading to Tonic; and Predominant, which is basically anything leading to Dominant. However, upon listening to the ways in which Plagal cadences get used, and how the chords on the perfect 4th above the Tonic get used as a sort of "home away from home" in some tunings, it is obvious to me that the stance taken by modern writers is an oversimplification, and that there are more remnants of the ideas of the two schools in modern music than one would initially think. Furthermore, the genres of music I write call for a reconstruction of at least some of the ideals of the old Germanic schools from the ground up. Thus, ideas from both schools, as well as a number of other ideas, find a home in my microtonal theory and practice. If the reader will bear with me, I shall use narrative set-ups and character metaphors to describe how the various harmonic functions act in composition and the way they relate to one another, and, furthermore, I'll eventually be looking at ways to extend this reconstruction of functional harmony into the microtonal realm. However, before I get into that, I must answer a few questions about how function relates to different parts of the chord.
Harmonic Information, Tonic, and Chord Structure
In modern theory, it is often contended that the third is the most important scale degree for determining harmonic information, followed by the root and the seventh while the fifth is the least important, however, I disagree with this assessment.
Instead, I contend that it's the root of a chord and the relationship between the chord root and the Tonic that dictates the bulk of the context for the function of the other notes in a given chord, with other bits of information being dictated by the relationship of other notes in the chord to both the Tonic and the actual chord root- do note that which note is considered to be the Tonic can in fact change based on additional context, such as the location of tritones- and, to a lesser extent, wolf fifths and wolf fourths- in a scale, as these, in combination with a tonality's direction of construction, can tonicize certain notes. From there, I think that only perfect fourths or perfect fifths that are either above or below a chord root can actually create stable frameworks for building chords, while dividing such intervals in two pieces without causing crowding creates the notes that impart character and color to chords. However, because perfect fifths are larger than perfect fourths, there's greater ease and a greater selection of options in dividing a perfect fifth without causing crowding than there is in doing the same with a perfect fourth.
I must also admit that I think additional harmonic information can be supplied by the likes of both otonal and utonal primodality, albeit my approach is a bit more unusual. While primes other than 2 can form the basis of tonality, it should be mentioned that the higher the prime involved as common numerator and or common denominator, the weaker the tonicization effect. Furthermore, I'm of the opinion that if you want to add intervals from segments with higher-prime denominators such as /3 or /5 to an otherwise /2^n segment to help flesh out what is essentially a Bass-Up tonality, it will usually work out best if that /3 or /5 interval is also a 2^n/ type of interval- in this case, 4/3 or 8/5. Similarly, I'm of the opinion that if you want to add intervals from segments with higher-prime denominators such as /5 or /7 to an otherwise /3*2^n segment to help flesh out what is essentially a Bass-Up tonality, it will usually work out best if that /5 or /7 interval is also a 3*2^n/ type of interval- in this case, 6/5 or 12/7.
Facets Derived from German Theory
Among the chief ideas that come from German Theory is that there are three basic, or primary functions, and that there are multiple operations that can be applied to these three basic functions in order to derive new functions. However, compared to those ideal functions, one of the three is in part original to my work.

Basic Diatonic Functions
The three basic functions have their roots in LCJI. The functions themselves are labeled as follows:
Tonic - This functionality has its roots in the fundamental at the root of both the harmonic and subharmonic series, which for all intents and purposes, can be thought of as 1/1, and, in octave equivalent systems, 2/1. To use a character metaphor for how the Tonic acts in functional harmony, the Tonic is the king of the Kingdom of Tonality- a very good king who not only exercises the highest authority in matters of governing the kingdom and does not tolerate challenges to his leadership, but also knows how be a top-notch confidante to his subjects both wherever and whenever possible. For more specifics on the functions of the Tonic, see the linked article.
Dominant - As per the name, and as noted on the Wikipedia article, the Dominant is the second most important after the Tonic, However, in contrast to what is stated about the Dominant in the article, there are several caveats which must be addressed in the realm of microtonality. Firstly, there's the matter of its origins- specifically, it is generated by the tonic as the first 3-limit interval and indeed the first nontonic note in the "majoresque" direction. Secondly, there's the matter of just what it does, as it typically serves as one, or often more, of the following- a primary creator of instability in the "majoresque" direction that requires the Tonic for resolution, the second most important melodic and or harmonic anchor after the Tonic- a function that requires it to be tuned with a great deal of accuracy in order to blend well with the Tonic- as well as a generator of many of the "majoresque" notes in a diatonic MOS, and or a discourager against the usage of other microtonally nearby pitches. Thirdly, one must take stock of the fact that, aside from the Unison and Octave, each octave-reduced harmonic and corresponding subharmonic interval come together to generate their own axis which has a preferred direction of travel[1] which is determined by a Tonality's direction of construction. Finally, one must take stock of the fact that when you take the notes that occur before the Tonic on each of these axes when moving in the preferred direction of travel and place them in a sequence, one finds that a clear hierarchy of functional strength based on the closeness of harmonic and subharmonic connection to the Tonic becomes apparent, with the 3/2 Perfect 5th away from the Tonic in a tonality's direction of construction naturally emerging as the note with the strongest connection to the Tonic, though it should be noted that the relationships in this hierarchy are quite sensitive to detuning, and can even be scrambled by such detuning. Thus, the term "Dominant"- in its most basic form as referred to in this article, and specifically at the root level- is restricted to where it only refers to such notes that occur roughly at a 3/2 interval away from the Tonic in the scale's direction of construction, with acceptable detuning levels being at around 3.5 cents from JI on either side. On the chord level, not only is the root level definition of the Dominant function at play, but it should also be noted that the Dominant does not see the Tonic occurring in the proximal tertian structure of its chord- that is, as a third or fifth. To use a character metaphor for how the Dominant acts in functional harmony, the Dominant is both the Head Steward of the Tonic's castle, and the one that executes the Tonic's directives as a Manager of Civil Service in the Kingdom of Tonality.
Serviant - Compared to the term "Subdominant" from music theory of old, the term "Serviant" (or, alternatively "Servient"), specifically at the root level, is restricted to those notes that occur roughly at a 4/3 interval away from the Tonic in the scale's direction of construction since the Serviant function is essentially the inverse of the Dominant function, and acts as a sort of counterweight to the Dominant relative to the Tonic. It typically serves as one, or often more, of the following— a primary creator of instability in the "minoresque" direction that can either be intensified with the dominant or resolved with the tonic, the third most important melodic and or harmonic anchor after the tonic and the dominant, a generator of many of the "minoresque" notes in a diatonic MOS, and or a discourager against the usage of other microtonally nearby pitches. To use a character metaphor for how the Serviant acts in functional harmony, the Serviant is a Servant who goes above and beyond the call of duty and acts as a confidante that observes things and reports back to the Dominant and Tonic about the way things are working both inside and outside the Tonic's castle due to its relationships to various Nontonic functions. Although one might think that the term "Subdominant" would be eligible for getting a similar treatment to the term "Dominant" here, the problems with such an option are threefold. Firstly, not all possible "Subdominant" harmonies have the same harmonic properties relative to the Tonic, as there is an extremely close connection between the Tonic and the 4/3 Perfect 4th. Secondly, in music built from the Treble downwards, the notes with these sorts of functions are actually located above the Dominant. Thirdly, in common parlance, "Subdominant" is often equated with "Predominant", however, while the Serviant does tend to resolve towards the Dominant, or else some other note that acts as a surrogate for the Dominant, the fact remains that it can also create plagal cadences, which break the modern Tonic-Dominant-Predominant paradigm and are better explained in part by the ideals of the two Germanic schools. On the chord level, not only is the root level definition of the Serviant function at play, but it should also be noted that a Serviant chord often sees the Tonic occurring in the proximal structure of its chord- that is, as either a third or fifth- which explains why Serviant chords are weaker than their Dominant counterparts in both Bass-Up and Treble-Down Tonalities.
Basic Diatonic Function-Deriving Operations
The way I see it, there are seven known operations which can be used to derive additional diatonic functions from the three basic functions listed above.
Stacking - The notes that are arrived at through stacking multiple instances of either 3/2 or 4/3 (or their tempered counterparts) are dubbed according to the number of instances stacked, and the nature of the notes separated by the interval being stacked. Thus, stacking two instances of the Dominant or the Serviant results in the creation of the "Bidominant" or "Biserviant" respectively. This concept comes from the German language's way of referring to the chord built on the second scale degree of the Diatonic scale as the "Doppeldominante", which literally means "Double Dominant".
Parallelism - Notes located in the same primary tetrachord as either the Tonic, the Dominant, or the Serviant but that don't crowd them tend to take on similar functions to said notes, with the caveat that functions derived from the Tonic in this fashion are still technically Nontonic functions. This process is one of two that create what in traditional music theory are referred to as "parallels" and "counter parallels". It should be noted that the ability of an interval to relate to the Tonic through Parallelism, as well as the surrounding of more dissonant intervals by consonant intervals in the same region displaying such relationships to the Tonic, results in a tendency towards harmonic stagnation.
Adjacency - Notes within a suitable voice leading distance from either the Dominant or Serviant tend to have the opposite function relative to the Tonic- this process even extends to the relationship between the Dominant and Serviant themselves. On the other hand, notes within this same kind of distance from the Tonic often tend to have their functions colored more by their relationships to both the Dominant and Serviant. This process is one of two that create what in traditional music theory are referred to as "parallels" and "counter parallels", however, unlike Parallelism proper, this process can establish these kinds of relationships outside the primary tetrachord.
Antipodism - Notes that are either opposite in pitch hue or nearly so due to being approximately half an octave away from the starting point are harmonically opposed to the starting point. Non-tonic notes related through this process tend to have the opposite function relative to the Tonic. For the notes related to the Tonic by this process, see Antitonic below.
Preparation - Notes that "prepare the way" for either a Dominant or a Serviant through any of the above operations, or through some other mechanism, relate to said notes by this process. Functions which have this kind of role relative to some other function are denoted with a "pre-" prefix here.
Detempering - When the comma or subchroma that separates a note from one of the three primary functions is not tempered out, it results in the appearance of notes with either similar functions to the Dominant or Serviant, or, in the case of this function being applied to the Tonic, a Nontonic function similar to one of the Chromatic functions. Often, though not always, these notes fall within the uncanny valleys of the three primary functions.
Neutralization - When one hybridizes Major and Minor Diatonic scale degrees of the same class or even tempers them together, one is using this process.
Facets Derived from Viennese Theory
Among the chief ideas that come from Viennese Theory is the idea that each degree has its own function relative to the Tonic. However, while in Viennese Theory proper, the degrees are strictly defined only relative to the cycle of fifths, I, for the realm of Microtonality, not only take stacks of 3/2 to form a key navigational axis called the "Diatonic Axis", but also additionally take things like Bass-Up tonality (that is, tonal music built from the low pitches upwards) and Treble-Down tonality (that is, tonal music built from the high pitches downwards) into consideration. On top of that, I also contend that virtually all of the functions described by Viennese Theory find their roots in specific combinations of the different operations described above on the basic functions from German Theory.
Derivative Diatonic Functions
I should point out that all of the scale degree functions described in Viennese Theory, as well as a few additional functions listed on this page, can be classified as first derivative functions because only one instance of any given derivational process is needed to reach them. Do note that of all the original Viennese functions, only the Mediant remains virtually unchanged from the original theories to this reconstruction, as another has been renamed, while others have been grouped together under new functions.
Supervicinant - This is any note that maps to 1\7 above the Tonic, and in fact, intervals in this vicinity have both Tonic Adjacent and Serviant Parallel functions, beyond that, however, the precise behavior of notes in this range is determined by both mappings and concrete tuning ranges, see the Supervicinant and Subvicinant Subtypes section for more discussion of this function.
Mediant - This is the note that maps to 2\7 from the Tonic in the scale's direction of construction and is named due to being roughly halfway between the Tonic and the Dominant. This is the first of the two diatonic scale degrees that are located relatively far from the Tonic along the Circle of Third Harmonics, and, as a consequence, not only has the most possibilities for realization, but also a tendency towards stagnation, leading to the historical designation as a "weak harmony". Aside from these, the properties that are central to the Mediant function are all most easily derived through the Tonic Parallel function and the Serviant Adjacent function, and in addition, Mediants have both Preserviant and Predominant functions. Furthermore, since there's such a large range of Mediants, there are a multitude of subtypes, see the Mediant Subtypes section for more discussion of this function.
Antitonic - This is a special case, see the Antitonic Subtypes section for more discussion of this function.
Contramediant - Compared to the term "Submediant" from traditional music theory, the term "Contramediant" may have a slightly different frame of reference, as while a "Submediant" is halfway between the Tonic and a "Subdominant", the "Contramediant" is halfway between the Tonic and the Serviant. The Contramediant is the note that maps to 5\7 from the Tonic in the scale's direction of construction, and is the second of two that are located relatively far from the Tonic along the Circle of Third Harmonics, and, as a consequence, is not only tied with the Mediant for having the most possibilities for realization, but also has a tendency towards stagnation, leading to the historical designation as a "weak harmony". From a functional standpoint, the properties that are central to the Contramediant function are most easily derived through the Tonic Parallel function and the Dominant Adjacent function, and in addition, Contramediants have both Preserviant and Predominant functions. Furthermore, since there's such a large range of Contramediants, there are a multitude of subtypes, see the Contramediant Subtypes section for more discussion of this function.
Subvicinant - This is any note that maps to 1\7 below the Tonic, and in fact, intervals in this vicinity have both Tonic Adjacent and Dominant Parallel functions, beyond that, however, the precise behavior of notes in this range is determined by both mappings and concrete tuning ranges, see the Supervicinant and Subvicinant Subtypes section for more discussion of this function.
Supervicinant and Subvicinant Subtypes
The Supervicinant and Subvicinant functions each have two subtypes that are common to traditional music theory and one subtype that's not diatonic at all, although leading tones have been specified according to their position and have been given distinct functions.
Specific Types of Supervicinant
The four subtypes of Supervicinant are as follows...
Supercollocant - This subtype of Supervicinant, although not found in Viennese Theory proper, is an interval that usually maps to both 1\7 and 2\24 in Bass-Up tonality. Additionally, it has the Antidominant function as typified by the root of the Neapolitan chord in Bass-Up tonality and the Antiserviant function in Treble-Down tonality. In actuality, two subtypes of Supercollocant exist- the "Proximosupercollocant", which always maps to both 1\7 and 2\24 in Bass-Up tonality, and the "Distosupercollocant", which maps to 1\7 and either 2\24 or 3\24 depending on a variety of factors, and is distinct from both Proximosupercollocant and Superabrogant only in finer tuning systems where it is usually more consonant, and thus, weaker. An example of a Proximosupercollocant is 256/243 while an example of a Distosupercollocant is 16/15.
Superabrogant - This subtype of Supervicinant is not a traditional diatonic function at all since it is an interval that maps to both 1\7 and 3\24 in Bass-Up tonality. As per this function's name, the intervals in this range are like Supercollocants in that they may cause listeners to forget the ending pitch's relationship to the starting pitch in voice-leading. However, they are noticeably too wide for them to convincingly pass off as being totally semitone-like since they feel as if they're rather disconnected from the Tonic, and furthermore, the occurrence of two successive instances of these sorts of intervals in the same melodic line in the same direction is liable to come across as jarring.
Superaequient - This subtype of Supervicinant is an interval that maps to 1\7 and either 3\24 or 4\24 depending on a variety of factors. It is so named for the equable heptatonic region above the Tonic, which comprises the bulk of its range, and for its capacity to straddle the line between the Supertonic and Superabrogant functions in voice-leading. Conspicuously, it is distinct from Supertonic and Superabrogant functions only in finer tuning systems, with the approximation ranges for 11/10 and 10/9 being located at its borders.
Supertonic - This subtype of Supervicinant is an interval that maps to both 1\7 and 4\24 in Bass-Up tonality and occurs above the Tonic as the second scale degree. However, it should be noted that the lower boundary of this function is situated at roughly 119/108 above the Tonic, since notes located at smaller distances from the Tonic are liable to cause listeners to forget the ending pitch's relationship to the starting pitch- something which Supertonics don't do under any circumstances. Conspicuously, one type of Supertonic is the "Bidominant", which is the function specifically of 9/8.
Specific Types of Subvicinant
The four subtypes of Subvicinant are as follows...
Subtonic - This subtype of Subvicinant is an interval that maps to both 6\7 and 20\24 in Bass-Up tonality and occurs above the Tonic as the seventh scale degree. However, it should be noted that the upper boundary of this function is situated at roughly 216/119 above the Tonic, since notes located at larger distances from the Tonic are liable to cause listeners to forget the ending pitch's relationship to the starting pitch- something which Subtonics don't do under any circumstances. Conspicuously, one type of Supertonic is the "Biserviant", which is the function specifically of 16/9.
Subaequient - This subtype of Subvicinant is an interval that maps to 6\7 and either 20\24 or 21\24 depending on a variety of factors. It is so named for the equable heptatonic region below the Tonic, which comprises the bulk of its range, and for its capacity to straddle the line between the Subtonic and Subabrogant functions in voice-leading. Conspicuously, it is distinct from Subtonic and Subabrogant functions only in finer tuning systems, with the approximation ranges for 9/5 and 20/11 being located at its borders.
Subabrogant - This subtype of Subvicinant is not a traditional diatonic function at all since it is an interval that maps to both 6\7 and 21\24 in Bass-Up tonality. As per this function's name, the intervals in this range are like Subcollocants in that they may cause listeners to forget the ending pitch's relationship to the starting pitch in voice-leading. However, they, like Superabrogants, feel as if they're rather disconnected from the Tonic, and furthermore, the occurrence of two successive instances of these sorts of intervals in the same melodic line in the same direction is liable to come across as jarring.
Subcollocant - This subtype of Subvicinant is the note typically referred to when people say "the leading tone", and an interval that usually maps to both 6\7 and 22\24 in Bass-Up tonality. Additionally, it has the Antiserviant function in Bass-Up tonality and the Antidominant function in Treble-Down tonality. Although triads built on this scale degree are regarded by some as simply incomplete Dominant Seventh chords, my own analysis, while acknowledging the functional similarities between the Subcollocant and the Dominant in Bass-Up tonality, sees this interval as functionally distinct from the Dominant due to the Subcollocant also being potentially related to the Mediant in the same way that the Dominant is related to the Tonic- a key functionality that is often exploited in circle progressions. In actuality, two subtypes of Subcollocant exist- the "Proximosubcollocant", which always maps to both 6\7 and 22\24 in Bass-Up tonality, and the "Distosubcollocant", which maps to 6\7 and either 21\24 or 22\24 depending on a variety of factors, and is distinct from both Proximosubcollocant and Subabrogant only in finer tuning systems where it is usually more consonant, and thus, weaker. An example of a Proximosubcollocant is 243/128 while an example of a Distosubcollocant is 15/8.
Mediant and Contramediant Subtypes
There are five basic types of Mediant, although only three of them are distinct in 24edo- you'd need to go to 41edo or 53edo to see all five. Similarly, there are five basic types of Contramediant, with only three of them being distinct in 24edo, so you'd need to go to 41edo or 53edo to see all five.
Specific Types of Mediant
The five subtypes of Mediant are as follows...
Proximomediant - This type of Mediant is mapped to 2\7 and 6\24 and is so named due to being located on the end of the Mediant range closest to the Tonic. Conspicuously, it is one of the possible the types of Mediant seen in Minor keys and is only distinct from the Mesoproximomediant in finer tuning systems where it is usually more dissonant. One subtype of Proximomediant is the "Triserviant", which is the function specifically of 32/27.
Mesoproximomediant - This type of Mediant is mapped to both 2\7 and either 6\24 or 7\24 depending on a variety of factors. It is so named due to being located between the proximal end of the Mediant range and the midline between the Tonic and the Dominant. Conspicuously, it is one of the possible the types of Mediant seen in Minor keys and is only distinct from the Proximomediant and Mesomediant in finer tuning systems where it's notable for containing the approximation range for 6/5 at its lower border and for being the fourth complement of the Superaequient, hence why it's not merely a simple compositing of the adjacent functions.
Mesomediant - This type of Mediant is mapped to both 2\7 and 7\24 and is so named due to being located along the midline between the Tonic and the Dominant. This type of Mediant is arguably the most dissonant, and is not a traditional diatonic function at all, and in fact, it doesn't serve well at phrase endings- rather, its Tonic Parallel function is only appropriate during the middle of musical phrases. Intervals with this type of function include 11/9 and 27/22.
Mesodistomediant - This type of Mediant is mapped to both 2\7 and either 7\24 or 8\24 depending on a variety of factors. It is so named due to being located between the distal end of the Mediant range and the midline between the Tonic and the Dominant. Conspicuously, it is one of the possible the types of Mediant seen in Major keys and is only distinct from the Mesomediant and Distomediant in finer tuning systems where it's notable for containing the approximation range for 5/4 at its upper border and for being the fourth complement of the Distosupercollocant, hence why it's not merely a simple compositing of the adjacent functions.
Distomediant - This type of Mediant is mapped to both 2\7 and 8\24 and is so named due to being located on the end of the Mediant range furthest from the Tonic. Conspicuously, it is one of the possible the types of Mediant seen in Major keys and is only distinct from the Mesodistomediant in finer tuning systems where it is usually more dissonant. One subtype of Distomediant is the "Quadridominant", which is the function specifically of 81/64.
Specific Types of Contramediant
The five subtypes of Contramediant are as follows...
Proximocontramediant - This type of Contramediant is mapped to 5\7 and 18\24 and is so named due to being located on the end of the Contramediant range closest to the Tonic. Conspicuously, it is one of the possible the types of Contraediant seen in Major keys and is only distinct from the Mesoproximocontramediant in finer tuning systems where it is usually more dissonant. One subtype of Proximocontramediant is the "Tridominant", which is the function specifically of 27/16.
Mesoproximocontramediant - This type of Contramediant is mapped to 5\7 and either 17\24 or 18\24 depending on a variety of factors. It is so named due to being located between the proximal end of the Contramediant range and the midline between the Tonic and the Serviant. Conspicuously, it is one of the possible the types of Contramediant seen in Major keys and is only distinct from the Proximocontramediant and Mesocontramediant in finer tuning systems where it's notable for containing the approximation range for 5/3 at its upper border, hence why it's not merely a simple compositing of the adjacent functions.
Mesocontramediant - This type of Contramediant is mapped to both 5\7 and 17\24 and is so named due to being located along the midline between the Tonic and the Serviant. This type of Contramediant is arguably the most dissonant, and is not a traditional diatonic function at all, and in fact, it doesn't serve well at phrase endings- rather, its Tonic Parallel function is only appropriate during the middle of musical phrases. Intervals with this type of function include 18/11 and 44/27.
Mesodistocontramediant - This type of Contramediant is mapped to both 5\7 and either 16\24 or 17\24 depending on a variety of factors. It is so named due to being located between the distal end of the Contramediant range and the midline between the Tonic and the Serviant. Conspicuously, it is one of the possible the types of Contramediant seen in Minor keys and is only distinct from the Mesocontramediant and Distocontramediant in finer tuning systems where it's notable for containing the approximation range for 8/5 at its lower border, hence why it's not merely a simple compositing of the adjacent functions.
Distocontramediant - This type of Contramediant is mapped to both 5\7 and 16\24 and is so named due to being located on the end of the Contramediant range furthest from the Tonic. Conspicuously, it is one of the possible the types of Contramediant seen in Minor keys and is only distinct from the Mesodistocontramediant in finer tuning systems where it is usually more dissonant. One subtype of Distomediant is the "Quadriserviant", which is the function specifically of 128/81.
Antitonic Subtypes
Notes that occur around half an octave away from the Tonic, on account of harmonies built on notes in this area tending to oppose that of the Tonic, are referred to by the term "Antitonic" by myself and others. It should be noted that the Antitonic is basically a first derivative function as it is derived from the Tonic through either perfect or imperfect Antipodism. In addition, the term "Antitonic" acts as a generic term for any of a group of diatonic functions found in this region. While some microtonal theorists insist that the Antitonic functionality is more fundamental than perhaps even the Dominant or Serviant, others, such as myself, disagree.
Specific Types of Antitonic
The exact outcome and specific function of any given Antitonic depends on whether or not the interval in question is an augmented fourth or a diminished fifth.
Sycophant - This type of Antitonic is mapped to both 3\7 and 12\24, and is named as such on account of it having a tendency to "kiss up to" and tonicize the Dominant- that is, to cause the Dominant to become a new Tonic- unless followed up by a different note such as some type of Mediant. A prototypical example of this type of Antitonic is 45/32.
Tyrant - This type of Antitonic is mapped to both 4\7 and 12\24, and it tends to contrast with the Tonic in a manner somewhat akin to that of a Dominant, but by sheer brute force and contrary harmonic nature, and indeed these brute force Dominant-esque tendencies are the source of the name "Tyrant". For example, if the Tonic harmony is Minor in nature, the Antitonic harmony will be Major- or more rarely, Supermajor- in nature. Furthermore, in scales such as the Locrian scale, any type of Serviant harmony tends to resolve towards some other type of substitute for a Dominant, often bypassing this type of Antitonic, though on rare occasions, a Tyrant will act as a leading tone to the Serviant. A prototypical example of this type of Antitonic is 64/45.
Chromatic Functions
These functions are either derived through Adjacency relative to some First Derivative Diatonic function, or else, are derived from the Primary Diatonic functions through a Chromatic function-deriving operation.
Primary Chromatic functions
The four basic Chromatic functions are as follows...
Superdislocant - This is a note that is to the Supercollocant what a Tyrant is to a Sycophant. Specifically, it is the result of the Tonic being altered by some kind of chromatic semitone upwards and thus being displaced by a Nontonic function which leads away from the Tonic proper.
Subdislocant - This is a note that is to the Subcollocant what a Tyrant is to a Sycophant. Specifically, it is the result of the Tonic being altered by some kind of chromatic semitone downwards and thus being displaced by a Nontonic function which leads away from the Tonic proper.
Protosycophant - This is a note which can tonicize the Dominant, but because its harmonies fail to completely oppose those of the Tonic, it fails to count as a true Sycophant. A prototypical example of this type of interval is 7/5.
Prototyrant - This is a note which can tonicize the Serviant, but because its harmonies fail to completely oppose those of the Tonic, it fails to count as a true Tyrant. A prototypical example of this type of interval is 10/7.
Basic Chromatic Function-Deriving Operations
The way I see it, there are at least one known operation which can be used to derive additional Chromatic functions from various Diatonic functions.
Displacement - This process results in a note that is near the Dominant or Serviant taking on similar functions to said notes rather than the opposite function, or, when applied to the Tonic, results in a Nontonic function that tends to want to lead away from the Tonic rather than towards it. This process is distinct from Detempering in that the notes created by this process are located at further distances from the note to which this process is applied.
Wolf Fifths, Wolf Fourths and the Uncanny Valleys of Harmony
As per Flora Canou's analysis[2], there are uncanny valleys on either side of each of the three primary functions. In this analysis, she states the following:
- From a historical perspective, meantone was discovered for a good reason. Letting it do its duty is of the greatest mercy. Not accounting for the discordance of wolf fifths or melodic bumps is equivalent to holding that meantone need not exist, and that most recent to modern theories are either failure or flukes based on wrong principles.
However, my contention is that while meantone doing its duty around the Tonic makes sense as 81/80 is really quite discordant, it seems that under certain circumstances, the average listener acquainted with 12edo music will not notice wolf fourths or wolf fifths unless they are explicitly pointed out, thus not only are there other methods of accounting for the discordance of wolf fourths and wolf fifths besides shunning them, but there are additional functions hiding in the shadows of the three primary functions, along with rules governing their usage, which shall be covered in this section.
Circumtonic Regions
The Circumtonic regions are the two main regions on either side of the Tonic, outside the Tonic's "event horizon". These intervals are invariably inside the Tonic's uncanny valleys, and the uncanny valleys around the Tonic, unlike those around the other two functions, are very deep, and as a result, wolf intervals around the Tonic are tolerable in ornamentation but not melody or harmony. Thus, these intervals cannot be directly approached from the Tonic, even melodically, and so they're usually avoided outside of modulation.
Supercommatic - This is a note that occurs at intervals from about 3.5 cents to roughly 25 cents above the Tonic. These intervals are little more than stepping stones in modulation, and extra intervals that can be used together with the Tonic for a sense of dissonance, or for a slightly less resolved version of a Unison or Octave.
Subcommatic - This is a note that occurs at intervals from about 3.5 cents to roughly 25 cents below the Tonic. As with Supercommatic intervals, these intervals are little more than stepping stones in modulation, and extra intervals that can be used together with the Tonic for a sense of dissonance.
Circumdominant Regions
The circumdomimant regions are the two main regions on either side of the Dominant proper, and since the uncanny valleys around the Dominant are not as deep as those around the Tonic, there is more room for actual first derivative diatonic functionality, as well as other functionalities. Note that together with the Dominant itself, these functions are collectively called "Protodominants", as there are many systems where what would be the Dominant fails to get distinguished from either one or the other of the functions listed here.
Geminodominant - This is a note that occurs roughly at intervals ranging from about 3.5 cents beyond 22/15 to about 3.5 cents short of the 3/2 perfect fifth in the scale's direction of construction. Although often overlooked or even outright shunned by traditional theorists, the Geminodominant is a legitimate diatonic function in terms of this analysis- albeit one only existing in non-meantone environments in which it is easily derived from the Dominant through detempering, occurring in 5-limit diatonic environments, and acting as a sort of "fraternal twin" to the Dominant, hence its name. Specifically, as typified by intervals like 40/27, Geminodominants are dissonant intervals that simultaneously act as alternatives to the Dominant in both chord progressions and chord construction, and often require resolution, though they also have a Preserviant function. The dissonance of this function relative to a chord root is useful in preventing tonicization of chords built on the traditional weak harmonies- the Mediant and the Contramediant- which also has the benefits of strengthening interrupted cadences and creating the sense of impending movement, but outside of these usages and well supported chords, this kind of thing is best avoided since things repel the similar but not identical. Apart from diatonic contexts, Geminodominants only rise to prominence in systems where what might otherwise function as a Dominant is found just short of the sweet spot range near the standard issue 3/2.
Pseudodominant - This is a note that occurs roughly at intervals ranging from about 3.5 cents to about 25 cents beyond the 3/2 perfect fifth in the scale's direction of construction. Because none of these intervals arise naturally in a 5-limit diatonic scale, and because they fall within one of the Dominant's uncanny valleys, it is rare to see this functionality outside of systems where what might otherwise function as a Dominant is found just beyond the sweet spot range near the standard issue 3/2. However, these intervals naturally arise in the Circle of Thirteenth Harmonics, in which case they have a Predominant function.
Circumserviant Regions
The circumserviant regions are the two main regions on either side of the Serviant proper, and since the uncanny valleys around the Dominant are not as deep as those around the Tonic, there is more room for actual first derivative diatonic functionality, as well as other functionalities. Note that together with the Serviant itself, these functions are collectively called "Protoserviants", as there are many systems where what would be the Serviant fails to get distinguished from either one or the other of the functions listed here.
Geminoserviant - This is a note that occurs roughly at intervals ranging from about 3.5 cents beyond the 4/3 perfect fourth to about 3.5 cents short of 15/11 in the scale's direction of construction. Although often overlooked or even outright shunned by traditional theorists, the Geminodominant is a legitimate diatonic function in terms of this analysis- albeit one only existing in non-meantone environments in which it is easily derived from the Serviant through detempering, occurring in 5-limit diatonic environments, and acting as a sort of "fraternal twin" to the Serviant, hence its name. As typified by intervals like 27/20, Geminoserviants are dissonant intervals that often act as a sort of Predominant and or as the inverses of Geminodominants. The dissonance of this function relative to a chord root is useful in preventing tonicization of chords built on the Mediant and the Contramediant, but outside of these usages and well supported chords, this kind of thing is best avoided. Apart from diatonic contexts, Geminoserviants only rise to prominence in systems where what might otherwise function as a Serviant is found just beyond the sweet spot range near the standard issue 4/3.
Pseudoserviant - This is a note that occurs roughly at intervals ranging from about 25 cents to about 3.5 cents short of the 4/3 perfect fourth in the scale's direction of construction. Because none of these intervals arise naturally in a 5-limit diatonic scale, and because they fall within one of the Serviant's uncanny valleys, it is rare to see this functionality outside of systems where what might otherwise function as a Serviant is found just short the sweet spot range near the standard issue 4/3. However, these intervals naturally arise in the Circle of Thirteenth Harmonics, in which case they have a Preserviant function.
Governing Rules
Commatic Repulsion - This rule is best summed up in Flora Canou's statement that things repel the similar but not identical. To illustrate this principle, let's take a look at the VImin chord as is present in meantone and contrast it to the situation outside of meantone. Believe it or not, the meantone VImin chord has no fewer than two separate functions relative to the Tonic. First of all, there's the Relative Minor functionality, which is 5/3–1/1–5/4 relative to the Tonic and can tonicize as a new Imin either temporarily, as in a deceptive cadence, or permanently as in a modulation. Secondly, there's the Tertiary Dominant functionality, which is 27/16-81/80-81/64 relative to the Tonic and, as the name suggests, acts as the Dominant of the Dominant's own Dominant. While both of these are fused together in meantone, these two functions are separated exactly by the syntonic comma in non-meantone environments, and the only way to use a VImin chord with both functions is to temper out the syntonic comma. As Flora Canou has stated:
- If the comma is not tempered out, the progression does not hold. The idea to force it is absurd. Fitting one function will leave the other emergent function[s] misplaced by a comma, which is easily the most catastrophic scene [musically] – the uncanny valley of harmony.
However, in non-meantone settings, it is possible to have a chord which shares its root with the Tertiary Dominant and shares both its third and fifth with the Relative Minor. Since such an arrangement results in a wolf fifth, and since the wolf fifth is a dissonance requiring resolution, one could argue that such a chord has a function distinct from the more traditional options- specifically one which is involved in interrupted cadences, as well as in starting cadences that "wind down" such as VImin-IVmaj-Imaj or even VImin-Vmaj-Imaj. This particular function is what I call the Major Contramediant Tensive.
Primary Adpositive Purity - This rule is that for every chord root located one step away from either the Tonic, Dominant or Serviant along the Circle of Fifths, there is a demand for the fifth of the chord in question to be within 3.5 cents of a just 3/2, though in the case of a chord that has a root located at two steps away from the Tonic along the along the Circle of Fifths, the fifth of the chord can be deliberately subjected to the process of Displacement as mentioned before and not run afoul of this restriction. However, chord roots that are located three or more steps away from the Tonic along the circle of fifths are not subject to the aforementioned restriction due to their distance. This means that the Tonic, Dominant, Serviant, Supertonic and Subtonic chords all demand a perfect fifth as the fifth of the chord, whether you are building the Tonality upwards or downwards, but wolf fifths can occur easily as the fifth of chords which are located three or more steps away from the Tonic.
Beyond Diatonic and Chromatic Functional Harmony
In addition to all the aforementioned Diatonic and Chromatic functions, as well as the detemperings of diatonic functions, there is an additional set of categories for dealing with the notes in between the various Diatonic scale degrees.
History
I've been in the process of developing this since well before I officially joined the Microtonal community, in fact, it all started for me with my discovery of the nature of the eleventh harmonic as a quartertone, however, while it is only thanks to a YouTuber who goes by "Quartertone Harmony" [3] that I've been able to fill in significant gaps in my theory, the reality is that the idea of extending Diatonic functional harmony to cover intervals between the standard scale degrees, can trace at least some of its roots back to the work of Ivan Wyschnegradsky.
Specifically, idea of extending Diatonic functional harmony to cover intervals between the standard scale degrees- an idea that has at least some roots in Wyschnegradsky's concept of "Major Fourth" and "Minor Fifth". However, I wanted to use LCJI as a basis for defining these intervals and thus decided to take 11/8 as being the just version of Wyschnegradsky's "Major Fourth", and while I drew up sketches based loosely on 24edo for early versions of this concept, I also realized that that two instances of 33/32 added up to an interval smaller than 2187/2048 but which had a similar function. Furthermore, since two instances of 11/8 resulted in an interval in the vicinity of a Major seventh, I decided to take stacks of 11/8 to form a second navigational axis which works together with the Diatonic Axis in order to define the microtonal functions positioned roughly halfway between the German and Viennese Diatonic functions, though there are a few other microtonal functions as well that are not immediately covered by this second axis.
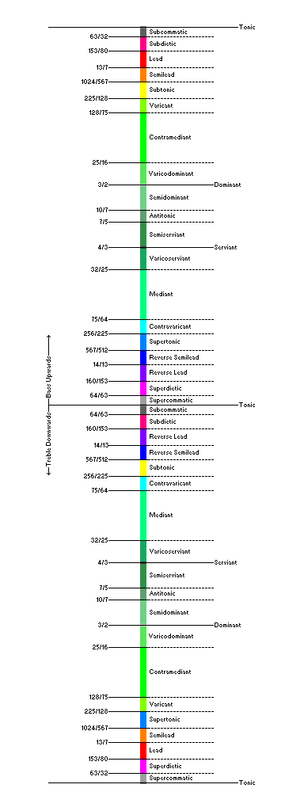
Most traditional music theorists know that there are basically two types of semitones- the diatonic semitone or minor second, and the chromatic semitone or augmented prime. They also know that a diatonic semitone and a chromatic semitone add up to a whole tone. The same things are true in Just Intonation as well as in EDOs other than 12edo or even 24edo. In a conversation between myself and Kite Giedraitis about this topic, Kite mentioned that there are two types of semitone in 3-limit tuning- a diatonic semitone of with a ratio of 256/243, and the aforementioned 2187/2048- a chromatic semitone that is otherwise known as the Apotome- which, when added together, add up to a 9/8 whole tone. Furthermore, Kite also mentioned how in 5-limit tuning, these same semitones exist alongside other semitones derived through alteration by 81/80. On one hand, adding 81/80 to 256/243 yields 16/15, and adding another 81/80 yields 27/25- two additional diatonic semitones. On the other hand, subtracting 81/80 from the Apotome yields 135/128, and subtracting another 81/80 yields 25/24- two additional chromatic semitones. When added up in the proper pairs- 16/15 with 135/128, and 27/25 with 25/24- the additional sets of semitones again yield a 9/8 whole tone. In light of all this, Kite argued that the familiar sharp signs and flat signs- which are used to denote the chromatic semitone- were never meant to denote exactly half of a whole tone, but rather, a whole tone minus a minor second.
Building on Kite's logic, I then decided to apply similar distinctions among quartertones, and thus make the argument that quartertones don't have to denote exactly one fourth of a whole tone in as of themselves, but rather, they only have to add up to a whole tone when paired up correctly. However, the catch was that for quartertones, there are sometimes multiple correct options, making things more complicated. I decided to define the musical functions of quartertones initially on an informal basis by drawing a distinction between the terms "Parachromatic" (from the prefix para- in both the senses of alongside and resembling[4], and the word chromatic) and "Paradiatonic" (from the same two senses of the prefix para- and the word diatonic) for purposes of classifying quartertone intervals. This was easy, since I had found that two instances of 33/32 added up to 1089/1024 rather than 2187/2048, and, since I had informally added the "para-" prefix (in the same senses) to both "Major" and "Minor" to create the terms Paramajor and Paraminor to better describe how 11/8 and 16/11 related to 128/99 and 99/64 respectively in order to describe how, for instance, the notes at 99/64 and 16/11 above the Tonic relate to each other in much the same way as major and minor intervals do, except that this relationship occurs in a context where the note halfway between them is actually part of the base scale rather than the two notes in question, and there's a different interval between said two notes than the base scale's chroma.
The way I see it, paradiatonic quartertones are analogous to diatonic semitones in that they are denoted as seconds, albeit inframinor seconds by default, while parachromatic quartertones are analogous to chromatic semitones in that they are denoted as primes, albiet as ultraprimes by default. However, the distinction goes further than that- a parachromatic quartertone and a paradiatonic quartertone add up to a diatonic semitone, while two parachromatic quartertones add up to a chromatic semitone. Given both these definitions for "paradiatonic" and "parachromatic", and given that a diatonic semitone and a chromatic semitone add up to a whole tone when paired correctly, it can be deduced that a whole tone can be assembled from three parachromatic quartertones and one paradiatonic quartertone. Because there are sometimes multiple correct options for assembling parachromatic and paradiatonic intervals to make a 9/8 whole tone, I ended up choosing the simplest configuration of paradiatonic and parachromatic intervals to assemble in order to create a 9/8 whole tone- a configuration that only requires one type of parachromatic quartertone and one type of paradiatonic quartertone. As a result of multiple factors, I ended up choosing the combination of three 33/32 parachromatic quartertones and one 4096/3993 paradiatonic quartertone as the JI basis for this in regards to both Diatonic theory and Alpharabian tuning, and, through interactions with others in the Xenharmonic community, I was later influenced by others on Discord to take MOS-based structural considerations into account. This eventually resulted in the first formal definition of a "parachroma" (an interval that can be easily tempered to equal half of a MOS-chroma), and later, the "parastep" (the interval that remains after subtracting as many parachromas from a Major MOS-step as possible without resulting in a negative interval). Finally, drawing from the concept of "parachromas" as applied to MOS-based contexts, I was able to finally give a formal definition of terms like "paramajor" (the result of adding a parachroma to either a MOS generator or its period-inverse) and "paraminor" (the result of subtracting a parachroma from a MOS generator or its period-inverse), which I had previously come up with on an informal basis.
The Realm of the Paradiatonic and the Parachormatic
In January of 2022, Quartertone Harmony posted a video in which he grouped together a series of functions he refered to in the video as the "shadow scale"[5], which I will refer to here as a paradiatonic scale since there are technically two of these, and this in turn led to the separation of Paradiatonic and Parachromatic harmonic functions for me. This whole concept of a "shadow scale", in addition to everything else discuss in this section, paves the way for my idea of MOS-Shadow theory, but, aside from how it applies to Diatonic-scale based functional harmony, MOS-Shadow theory is another whole discussion for another time.
The Paradiatonic Scales
The Paradiatonic scales from a given tonic acts as a sort of "second shelf" of that tonality. Note that scale degrees in parentheses are optional.
The Bright Paradiatonic Scale consists of the following scale degrees as analyzed relative to Viennese Theory's scale steps:
I, tII/dbIII, (dIII), tIV, dV, (dVI), tVI/dbVII, tVII
The Dark Paradiatonic Scale consists of the following scale degrees as analyzed relative to Viennese Theory's scale steps:
I, dbII tII/dbIII, (dIII), tIV, dV, (dVI), tVI/dbVII
While the Diatonic scale itself has seven notes, the two Paradiatonic scales each have eight notes, furthermore, the tunings of each note in each Paradiatonic scale not only depend upon the exact tuning of the Diatonic scale used as a basis, but also vary considerably when it comes to the notes of the Paradiatonic that occur between the main Diatonic interval category ranges.
Basic Paradiatonic Functions
Out of the various functions found in the Paradiatonic scales, four of them- specifically, the tII/dbIII, tIV, dV and tVI/dbVII- can be considered basic, while the other three are first derivatives. As with the three basic diatonic functions, the four most basic paradiatonic functions have their roots in LCJI. In the order listed, the tII/dbIII, tIV, dV and tVI/dbVII functions are the following...
Contravaricant - Named in contrast to the Varicant function, this is an interval that maps to both 1\5 and 5\24 in the scale's direction of construction, lying roughly in the middle of the 4/3 interval separating the Tonic and the Serviant above it. Intervals in the Contravaricant region often don't consistently act as either seconds or thirds, or even act as a cross between a second and a third, only without potential for crowding in chords. In Bass-Up tonality, this functionality is first encountered in the form of 8/7, though 7/6 is another notable interval included in this range, with intervals in this range having Predominant, Preserviant, and Dominant Parallel functions, as well as an overlap between Tonic Adjacent and Tonic Parallel functions. There are two different subtypes of this function that differ from each other based on how they are approached in interval stacking, the "Pseudobidominant", which arises from stacking two Pseudodominants, and the "Pseudotriserviant", which arises from stacking three Pseudoserviants.
Intersubiant - This is an interval that maps to both 3\7 and 11\24 in the scale's direction of construction and comprises the intervals ranging from around 3.5 cents short of 15/11 to around 3.5 cents beyond 11/8. Like both the Serviant and the Sycophant, intervals in this region have a Predominant function, however, this predominant function is weaker than that of the surrounding interval regions since they neither act as a counterweight to the Dominant like a Serviant nor do they completely tonicize the Dominant like a Sycophant- at least to those who are more familiar with quartertones. What is even less expected is that these same intervals also have Preserviant and Mocktyrant functions. Since the Intersubiant is not found in the Tonic's quartertone field, there is a tendency for Intersubiant chords to be preceded and or followed by other chords with roots in the same quartertone field, though one could also reasonably approach it from the Tonic, the Serviant, some kind of Contramediant, some kind of Supervicinant, or, in some tuning systems, certain kinds of Mediant. In Bass-Up tonality, this functionality has its roots in the eleventh harmonic.
Interregnant - This is an interval that maps to both 4\7 and 13\24 in the scale's direction of construction and comprises the intervals ranging from around 3.5 cents short of 16/11 to around 3.5 cents beyond 22/15. Accordingly, intervals in this region behave as a cross between a Tyrant Antitonic on one hand and a Dominant on the other in that they often contrast with the Tonic through some combination of harmonic connection and brute force contrast, though it unexpectedly has decent Predominant and Mocksycophant functions. Like the Intersubiant, the Interregnant is not found in the Tonic's quartertone field and is either very distant from the Tonic along the circle of fifths or is completely missed by said circle of fifths, thus, there is a tendency for Interregnant chords to be preceded and or followed by other chords with roots in the same quartertone field. Conspicuously, the distance between the Interregnant is only about a Minor Second- or, at the very most, a Supraminor Second- away from the Intersubiant, so as a result, the Interregnant can be both a set-up and a follow-up to the Intersubiant. In Bass-Up tonality, the Interregnant functionality has its roots in the eleventh subharmonic.
Varicant - Just as a Mediant lies roughly in the middle of the 3/2 interval separating the Tonic and the Dominant above it, a Varicant lies roughly in the middle of the 4/3 interval separating the Dominant and the Tonic above it. Intervals in this region often don’t consistently act as either sixths or sevenths, or even act as a cross between a sixth and a seventh, only without potential for crowding in chords- effectively straddling the border between these two diatonic categories, hence the name "Varicant", from Latin "vāricō"[6]. This is an interval that maps to both 4\5 and 19\24 in the scale's direction of construction. In Bass-Up Tonality, this functionality is first encountered in the form of the 7/4 interval, though 12/7 is another notable interval included in this range. While many microtonalists think of 7/4 as being purely a type of seventh- and indeed, it most commonly acts as a sort of subminor seventh- I counterargue based on this same interval's relationships with 11/8 in particular that 7/4 is not merely a type of seventh, but rather, a type of a cross between a sixth and a seventh, with such a property explaining why 14/11 is generally considered to be a type of third. Furthermore, in contrast to the Subtonics of Bass-Up Tonality, Varicants are liable to act as Predominants, Preserviants, and Serviant Parallels, as well as display an overlap between Tonic Adjacent and Tonic Parallel functions. There are two different subtypes of this function that differ from each other based on how they are approached in interval stacking, the "Pseudotridominant", which arises from stacking three Pseudodominants, and the "Pseudobiserviant", which arises from stacking two Pseudoserviants.
Derivative Paradiatonic Functions
Subgradient - This is a note that occurs at intervals between roughly 48/25 above the Tonic and roughly 25 cents below the octave reduplication of the Tonic. These intervals tend to act as parachromatic alterations of either the Tonic, or, more rarely in Bass-Up Tonality, the Subcollocant- however, there are functional differences between a Subgradient and a Subcollocant in Bass-Up Tonality. In Bass-Up Tonality, Subgradients are often more likely to be passing tones than Subcollocants, and, when they’re not merely passing non-chord tones, they are often harder to approach and or follow up without creating some kind of awkward tonal disconnect, with such a disconnect being especially noticeable for intervals like 64/33. Furthermore, whereas a Lead can resolve to the Tonic in part through a strong harmonic connection, a Subgradient is much more likely to do so through sheer brute force, and even these cases require a proper set-up, as otherwise, the awkward tonal disconnect between the Subgradient and the Tonic is likely to result in the Subgradient resolving back down to either the Subcollocant or the Subabrogant. As if that weren't enough, the Subgradient also has the Antintersubiant function. This function used to be called the "Subdietic", though that term has since been restricted to a related composite function (see below on Composite Functions).
Supergradient - This is a note that occurs at intervals between roughly 25 cents above the Tonic and 25/24 above the Tonic. These intervals tend to act as parachromatic alterations of either the Tonic, or, more rarely in Bass-Up Tonality, the Supercollocant. However, there are a few functional differences between a Supergradient and a Supercollocant in Bass-Up Tonality that are worth considering. For starters, Supergradients are often more likely to be passing tones than Supercollocants, and, when they’re not merely passing non-chord tones, they are just as liable to resolve upward through some sort of semitone-like motion to some form of Supercollocant or Superabrogant, as they are to resolve downwards toward the Tonic, a property which intervals like 33/32 in particular are apt to demonstrate. Furthermore, whereas a Supercollocant can resolve to the Tonic in part through a strong harmonic connection, a Supergradient is much more likely to do so through sheer brute force when such a resolution is noticeable. As if that weren't enough, the Subgradient also has the Antinterregnant function. This function used to be called the "Superdietic", though that term has since been restricted to a related composite function (see below on Composite Functions).
Parachromatic Functions
These are quartertone functions that are not on the Paradiatonic Scale. Of these, there are only two basic functions...
Superobstant - This is a note which, in Bass-Up tonality, is mapped to 9\24. This region is characterized by intervals that don’t consistently act as either thirds or fourths, or even act as a cross between a third and a fourth, as well as by intervals that act as parachromatic alterations of either the Mediant or the Serviant. As per the name, which comes from "super-" and "obstant", the latter of which comes from Latin "obstō"[7], intervals in this region are also generally more dissonant and have a tendency to disrupt both chords and melodies, leading to their avoidance in chords outside of deliberate dissonances. Chords of this type have Preserviant, Preintersubiant and Preinterregnant functions as well as Premediant functions.
Subobstant - This is a note which, in Bass-Up tonality, is mapped to 15\24. This region is characterized by intervals that don’t consistently act as either fifths or sixths, or even act as a cross between a fifth and a sixth, as well as by intervals that act as parachromatic alterations of either the Dominant or the Contramediant. As per the name, which comes from "sub-" and "obstant", which, as mentioned before, comes from Latin "obstō", intervals in this region are also generally more dissonant, leading to their avoidance in chords outside of deliberate dissonances. Chords of this type have Predominant, Preintersubiant and Preinterregnant functions, as well as Precontramediant functions, and, perhaps very tellingly, tend to utilize Diminished Fourths instead of Major Thirds due to the functions of the Subgradient- which usually gets incorporated into these kinds of chords.
Diatonic, Paradiatonic, and the Tonic's Proximal Pythagorean Aura
One of the things that Quartertone Harmony has found and mentioned[8] is that when dealing with quartertones, there seems to be something about a given 12-tone scale in 24edo which assures that notes in that same field will sound like they go together. However, in systems such as 159edo, you begin to see that things are slightly more complicated, as this distinctive atmosphere or quality turns out to be around 20 cents at widest and seems to surround and be generated by notes related to the Tonic by Pythagorean intervals that aren't all that far away from the Tonic, hence the term proximal Pythagorean aura to refer to it. Notably, the proximal Pythagorean aura is at its thickest at around six or seven steps away from the Tonic in either direction along the circle of fifths, and extends along the circle of fifths on either side of these areas from two steps away from the Tonic to eleven steps away from the Tonic. The presence of this aura explains things related to the uncanny valleys around the Dominant and Serviant- namely why these uncanny valleys are not as deep or as wide as those around the Tonic, and why simple intervals with single factors of prime 5 seem to be at least somewhat "in key" relative to the Tonic. It should be noted that the Tonic, the Dominant, and the Serviant work together with this aura to define safe regions for field shifts that are guaranteed to not come across as jarring. Intervals outside of this aura, such as most paradiatonic intervals, must abide by certain rules in order to not come across as jarring.
Additional Composite Functions
Notes on the boundaries of functional regions have multiple functions due to occurring at the boundary between different functions, the process by which this happens is known as Compositing. As for the actual composite functions themselves, there are quite a few of them.
Subdietic - This function is a compositing of Subcommatic and Subgradient, and as Subcommatic is part of its nature, it is effectively repelled harmonically. It should be noted that this is one of only a handful of composite functions which are formed by the overlap between different functional regions rather than merely being located at a boundary.
Superdietic - This function is a compositing of Supercommatic and Supergradient, and as Supercommatic is part of its nature, it is effectively repelled harmonically. It should be noted that this is one of only a handful of composite functions which are formed by the overlap between different functional regions rather than merely being located at a boundary.
Subsanguinant - This function is one of two "bleeding tone" functions- hence its Latin-derived name- and is a compositing of Subgradient and Proximosubcollocant functions, and thus, has a more tense feel than a Proximosubcollocant alone. It should be noted that this function is formed by the overlap between different functional regions rather than merely being located at a boundary.
Supersanguinant - This function is one of two "bleeding tone" functions- hence its Latin-derived name- and is a compositing of Supergradient and Proximosupercollocant functions, and thus, has a more tense feel than a Proximosupercollocant alone. It should be noted that this function is formed by the overlap between different functional regions rather than merely being located at a boundary.
Submaculant - This function is a compositing of Subgradient and Subdislocant, and thus is like the chromatic version of the Subsanguinant.
Supermaculant - This function is a compositing of Supergradient and Superdislocant, and thus is like the chromatic version of the Supersanguinant.
Acuotyrant - This function is a compositing of Prototyrant and Interregnant in Bass-Up Tonality, and although an interval like this generally fails to truly oppose the harmonies of the Tonic, it nevertheless operates more on the side of brute force when it contrasts with the Tonic.
Gravosycophant - This function is a compositing of Protosycophant and Intersubiant in Bass-Up Tonality, and although an interval like this generally fails to truly oppose the harmonies of the Tonic, it nevertheless often runs a high risk of tonicizing the Geminodominant.
Gravotyrant this function is a compositing of Prototyrant and Interregnant in Treble-Down Tonality, and although an interval like this generally fails to truly oppose the harmonies of the Tonic, it nevertheless operates more on the side of brute force when it contrasts with the Tonic.
Acuosycophant - This function is a compositing of Protosycophant and Intersubiant in Treble-Down Tonality, and although an interval like this generally fails to truly oppose the harmonies of the Tonic, it nevertheless often runs a high risk of tonicizing the Geminodominant.
Extra Functions of Prime Harmonics and Subharmonics
It should be noted that there are other layers of function besides those oriented around the 3-limit. These are detailed here.
Paradominant - This function typically appears along prime axes other than that of the 3-limit in which they take Dominant-like function. Thus, for example, in Bass-Up Tonality, the note at 5/4 above the Tonic, being a direct prime harmonic of the Tonic, gets to serve this function in addition to its Mesodistomediant function as defined by the 3-limit, with the Paradominant function emerging mainly in a series of 5/4-based motions leading to the Tonic. When considered alongside the actual Dominant function of 3/2, however, Paradominants take on the function of Predominant owing to the fact that the Dominant function of 3/2 is actually stronger than that of any predominant due to being closer to the fundamental.
Paraserviant - This function is essentially the inverse of the Paradominant function, and acts as a sort of counterweight to the Paradominant relative to the Tonic. Like the Paradominant function, it typically appears along prime axes other than that of the 3-limit in which they take Serviant-like function. Thus, for example, in Bass-Up tonality, the note at 8/5 above the Tonic, being a direct prime subharmonic of the Tonic, gets to serve this function in addition to its Mesodistocontramediant function as defined by the 3-limit. When considered alongside the actual Serviant function of 4/3, however, Paraserviants take on the function of Preserviant since the Serviant function of 4/3 is stronger.
References
- ↑ Quartertone Harmony - Beyond the Circle of Fifths SD 480p
- ↑ Analysis on the 13-limit just intonation space: episode ii. Flora Canou. Xenharmonic Wiki.
- ↑ Quartertone Harmony - YouTube
- ↑ Wiktionary: para- #Etymology 1
- ↑ Quartertone Harmony - Harmonic Functions of Quartertones SD 480p
- ↑ Wiktionary: varico #Latin
- ↑ Wiktionary: obsto #Latin
- ↑ Quartertone Harmony - The Truth About Quartertone Melodies