User:FloraC/Analysis on the 13-limit just intonation space: episode ii

Preface

The Previous Episode mainly addresses how to make sense of the 13-limit JI space. On that basis, this one goes much in depth with the practical side such as interval semiotics, chord construction, chord progression, and some tempering possibilities.

More fundamental context can be found in Fundamental Principles to Musical Sense and There Is Not a Third Side of the River.

Chapter I. Ionian versus Mode 8

Scales generated by octaves and fifths i.e. the 2nd and 3rd harmonics, has proved to be quintessential in functional harmony. It is easy to see how functional harmony unfolds through fifth disposition, up to octave equivalence. The diatonic scale is such an instance. It has also been explained how the major tonality demonstrates the presence of harmonics. Now we investigate if there is a specific diatonic mode implied by the major tonality.

In 5-limit JI, the Ionian mode is the clear favorite. The logic is that the diatonic scale can be generated by the three functional positions of the classical major triad, and the result is in Ionian. In 13-limit JI, things must be re-evaluated. The chord cannot stay classical. More is different. Let us consider the first 16 harmonics. Mode 8 is a good candidate subject to our account since it is a very coherent scale and chord structure in itself. Assume the root is C, we see each step in mode 8 is mapped to C, D, E, F+, G, Ad, Bb, and B by the interval category scheme introduced in the Previous Episode.

Figure: first 16 harmonics in neutral circle-of-fifths notation on C

If neutral intervals are taken as exactly half of what it splits, the diatonic generator steps of each step in mode 8 are 0, +2, +4, +5/2, +1, -1/2, -2, and +5, with an average of +3/2. The number has the meaning such that it can be compared to the average brightness of the diatonic modes shown in the following table.

Brightness of diatonic modes

Mode	UDP	Average Brightness
Lydian	6|0	+3
Ionian	5|1	+2
Mixolydian	4|2	+1
Dorian	3|3	0
Aeolian	2|4	-1
Phrygian	1|5	-2
Locrian	0|6	-3

Hence, the brightness of mode 8 is halfway between Ionian and Mixolydian. The two diatonic modes' only difference is the quality of the seventh. Indeed, both the minor seventh (precisely the subminor seventh) and the major seventh are present in mode 8, so it all narrows down to which seventh should be the default. This is a question where, when suddenly asked about, one tends to refer to jazz chord notation for an answer – jazz has chosen the minor seventh. Actually, tonality is not a fixed chord structure built on tonic. In common practice, tonality is established through progressions of various functions, dominant–tonic being the most important, and regarding the dominant seventh chord, although itself contains a minor seventh, its third is a major seventh on the tonic. It is this third that is the spirit of the major tonality. For that reason, Ionian remains the most favorable general framework for mode 8, and by extension, for the major tonality in 13-limit JI.

Chapter II. Generic Rooted Chord Construction

It has been demonstrated in the Previous Episode that septimal harmony is characterized by semiquartal harmony, a seemingly different chord construction scheme from the traditional tertian harmony. A question then arises as what essence is abstracted by the chord construction scheme, and what role is played by tertian harmony in the context of 13-limit JI. To answer this, we will investigate how tertian harmony finds harmonics in the process of chord construction, and how each chord contrasts with its negative version.

Any two consecutive odd harmonics in the first 16 give rise to the following intervals.

Interval	Notation	Interval Class
3/1	C–G	Perfect twelfth
5/3	G–E	Major sixth
7/5	E–Bb	Subdiminished fifth
9/7	Bb–D	Supermajor third
11/9	D–F+	Neutral third
13/11	F+–Ad	Subminor third
15/13	Ad–B	Superultramajor second

It seems that all kinds of intervals emerge out of the odd harmonics, but when it comes to compact voices, we find patterns. One prominent frame would involve the split of mode 8 into two octaves. The first octave consists of mode 4; the second octave consists of the other four tones in mode 8.

Figure 2: double-octave voicing of mode 8

Interval	Notation	Interval Class
5/4	C–E	Major third
6/5	E–G	Minor third
7/6	G–Bb	Subminor third
9/7	Bb–D	Supermajor third
11/9	D–F+	Neutral third
13/11	F+–Ad	Subminor third
15/13	Ad–B	Superultramajor second

Observably, all except for the last interval are sorted into thirds. It should be noted that this third is to be understood in a loose sense. 9/7 is a third, a supermajor one. 11/9, a neutral one. 13/11, a subminor one. That definitely unveils tertian harmony's central role in 13-limit JI, but moreover, semiquartal harmony is inevitable as well in light of their close association.

To get an impression about this association, the pitch spectrum can be viewed as composed of segments such that each octave has two segments, with the lower segment ranging from 1 to 3/2, and the upper segment ranging from 3/2 to 2/1. The lower segment spans a fifth, so it calls for tertian construction, for which the classical triads are examples as 5/4 is in this segment. The upper segment spans a fourth, so it calls for semiquartal construction, for which the septimal triads are examples as 7/4 is in this segment.

Applying all that has been discussed, the just major chord, built on C, can be extended as

• CM (C–E–G)
• C7 (C–E–G–Bb)
• C9 (C–E–G–Bb–D)
• C11 (C–E–G–Bb–D–F+)
• C13 (C–E–G–Bb–D–F+–Ad)
• C15 (C–E–G–Bb–D–F+–Ad–B)

It is basically the traditional jazz chord notation, with some deviation. Specifically, the "eleventh" is by default semiaugmented and literally represents the 11th harmonic; the "thirteenth" is by default neutral and literally represents the 13th harmonic. The "fifteenth" is similar. The symbols are mostly logical except that C5 has been taken to indicate a bare fifth, and that CM is used in place of where C5 is supposed to be.

In summary, the just major chord is a four-segment eight-tone chord spanning two octaves, as

[math]\displaystyle 1–5/4–3/2–7/4–9/4–11/4–13/4–15/4[/math]

According to the principles of harmony dualism, it has a negative version with the same number of segments and the same number of tones in each segment (besides the root and the fifth, which are on the boundaries), so that every tone has something to contrast to in the inverse. The development of the negative version can be concisely described by the intrasegmental inversion rule:

Intrasegmental inversion rule

The operation of inversion should flip each segment in place.

The negative version, the just minor chord, is therefore

[math]\displaystyle 1–6/5–3/2–12/7–24/11–8/3–16/5–48/13[/math]

Indeed, the structure is similar. The thirds contrast by 25/24. The hemitwelfths contrast by 49/48. The ninths and the elevenths contrast by 33/32. The thirteenth and the fifteenth contrast by 65/64. Furthermore, both versions are dyadically concordant since all the dyads are in the 21-odd-limit tonality diamond. Besides the root and the fifth, taking any intervals from the two chords typically makes sense. The figure below illustrates all the segments and the inversion.

Figure 3: just major chord and just minor chord

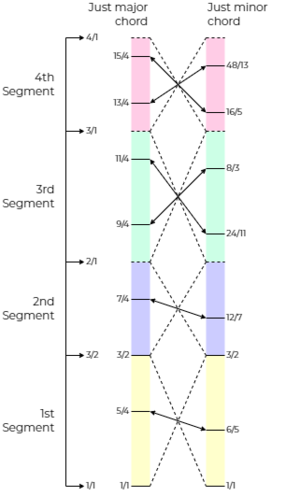
More readily, we can take individual segments as chords. These chords are neat in that each segment can be taken to represent one of the primes in 5, 7, 11, and 13. For example, the first segment is the just major/minor triad; the second segment is the just major/minor semiquartal triad, with the semiquartal voicing rule:

Semiquartal voicing rule

The fifth should be transposed to the second octave if only the upper segment is used.

We take the third segment to make really basic use of undecimal intervals. It has a very pleasant sound. Called the just micromajor tetrad and the just microminor tetrad, the two versions are

[math]\displaystyle 1–9/8–11/8–3/2 \\ 1–12/11–4/3–3/2 [/math]

We take the fourth segment to make really basic use of tridecimal intervals, though it involves a classical interval as well. Called the just micromajor semiquartal tetrad and the just microminor semiquartal tetrad, the two versions are

[math]\displaystyle 1–13/8–15/8–3 \\ 1–8/5–24/13–3 [/math]

The names will be explained in the next chapter.

Since 5/4 and 11/8 are in the lower segment, and 7/4 and 13/8 are in the upper segment, we notice they tend to work together. Superposing the first and the third segment produces a supercompact segment. Called the just major pentad and the just minor pentad, the two versions are

[math]\displaystyle 1–9/8–5/4–11/8–3/2 \\ 1–12/11–6/5–4/3–3/2 [/math]

9/8 or 11/8 can be omitted to maximize the concordance; the same can be said for 12/11 or 4/3 in the negative version. But they should be present if complete contrast between the two chords is desired.

Similarly, the second and the fourth segment can be superposed. Called the just major semiquartal pentad and the just minor semiquartal pentad, the two versions are

[math]\displaystyle 1–13/8–7/4–15/8–3 \\ 1–8/5–12/7–24/13–3 [/math]

13/8 or 15/8 in the positive version and 8/5 or 24/13 in the negative version can be omitted for the same reason as above.

Concatenating the two supercompact segments produces the supercompact voicing of the chord, whose positive version is identical to mode 8. The two versions are

[math]\displaystyle 1–9/8–5/4–11/8–3/2–13/8–7/4–15/8 \\ 1–12/11–6/5–4/3–3/2–8/5–12/7–24/13 [/math]

Even more extensions can be attached to the fully extended chord without breaking its logic. It is just that the identities of higher harmonics get progressively weaker, until vanishing in the sea of harmonic entropy. The ultra-extended contruction of the chord includes an extra segment on the two octaves, featuring harmonics 19 and 21. The chord would be

[math]\displaystyle 1–5/4–3/2–7/4–9/4–11/4–13/4–15/4–19/4–21/4 \\ 1–6/5–3/2–12/7–24/11–8/3–16/5–48/13–32/7–96/19 [/math]

It thus has 17 and 23 left out as those harmonics conflict with the root or the fifth. Following the aesthetics of tertian harmony, they will re-appear in diminished chords, detailed in Chapter IV. After all, they are really on the edge. Bordering on the average JND of human beings, the difference between 21/20 and 22/21 is subtle enough, not to mention what is implied by the 23rd harmonic.

Or less can be used. Cutting off the second octave, the harmonic seventh chord and the harmonic sixth chord are

[math]\displaystyle 1–5/4–3/2–7/4 \\ 1–6/5–3/2–12/7 [/math]

Chapter III. Primodality and Nonrooted Chord Construction

So far, it is only the beginning of the story. The richness of JI harmonic gestures comes from sources other than rooted chords.

The primodality paradigm provides magnificent insight to building these chords. All primodal series are highly coherent chords on their own, regardless of what may be suggested by the name. The way it sorts JI intervals into primodal series characterizes the chords by tones which are not only dyadically concordant, but also mutually consolidating. In particular, such a chord is concordant as long as the highest irreducible dyad relative to the root is considered so, since the supreme limit of all the dyads equals that of the highest irreducible dyad relative to the root.

It finds the series by putting forward a prime harmonic, say 11. The associated series is formed by all subsequent harmonics, written out as

[math]\displaystyle 11:12:13:14:15:16:17:18:19:20:21:22:\ldots[/math]

That is the /11 (read: over-eleven) series. Converting it to the conventional notation to show all the dyads about the root, we see it indeed features 11's on the denominator, and the supreme limit of the chord is no larger than that of the highest irreducible dyad:

[math]\displaystyle 1–12/11–13/11–14/11–15/11–16/11–17/11–18/11–19/11–20/11–21/11–2/1–\ldots[/math]

Primodality theorists has somehow not been concerned with harmonic dualism, so a new development follows. There are two adaptations to be made before its inverse, the 11/ (read: eleven-over) series, could be enabled. First, the dyads should be omitted if they break the concordance on inversion. Setting the threshold of concordance to a certain odd limit, those dyads would conflict with the 3rd harmonic, though they work in well supported harmony, quick passing tones or ornaments. Intervals that are not invertible in the 13-limit 21-odd-limit are 10/9, 11/9, 13/9, 14/9, 16/9, 13/11, 14/11, 16/11, 20/11, 14/13, 16/13, 20/13, 16/15, 22/15, 26/15, 28/15, 22/21, 26/21, 32/21, and 40/21. Second, the voicing should be arranged into tertian–semiquartal harmony, with one or two tones reasonably placed in each segment. To achieve it, the intrasegmental inversion rule still elegantly holds.

As a start, consider the following subset tetrads in the lower segment. This is the standard form of the undecimal tetrad. Named the undecimal micromajor tetrad and the undecimal microminor tetrad, the two versions are

[math]\displaystyle 1–11/10–11/8–3/2 \\ 1–12/11–15/11–3/2 [/math]

The names are derived in light of the implications of how 11/10 inverts to 15/11, and how 11/8 inverts to 12/11. Micromajor or microminor are members of microtonalities. Literally, a microtonality refers to a neophyte of tonality, characterized by chromas of the commatic, subcommatic or supercommatic level. In this case, 11/10 contrasts to 12/11, and 11/8 contrasts to 15/11, both by 121/120, the biyatisma. The separation is incredibly tiny, yet it could not be more real. The subtlety in the two chords is one of the greatest charms of the 2.3.5.11 subgroup.

To further understand microtonality, let us take a look at the distribution of harmonics in the octave. As tonality can be viewed as resulted from the primary subdivision of the octave, microtonality can be viewed as resulted from the secondary subdivision. Just like how 5/4 and 6/5 are symmetric about the axis halfway between 1 and 3/2, 11/8 and 15/11 are symmetric about the axis halfway between 5/4 and 3/2, and 12/11 and 11/10 are symmetric about the axis halfway between 1 and 6/5.

Figure 4: illustration of tonalities resulted from octave subdivision

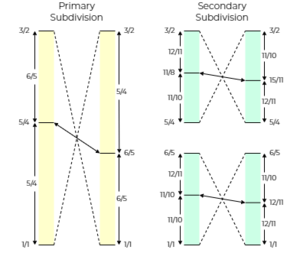
Another concerning topic is the voicing. For either version, the second and the fourth are used in place of the third. We have adopted this very construction in the undecimal segment of the rooted chord.

Next, consider the following subset tetrads in the upper segment. This is the alternative form of the undecimal tetrad. Named the undecimal micromajor semiquartal tetrad and the undecimal microminor semiquartal tetrad, the two versions are

[math]\displaystyle 1–11/7–11/6–3 \\ 1–18/11–21/11–3 [/math]

Notice how 11/7 inverts to 21/11, and how 11/6 inverts to 18/11. The micromajor is said for 11/6 as opposed to 20/11, and the microminor is said for 18/11 as opposed to 33/20. Even with a strange negative chroma (121/126), the upper segment is just as amazing as the lower.

For extended forms, we concatenate them. Named the undecimal micromajor chord and the undecimal microminor chord, the two versions are

[math]\displaystyle 1–11/10–11/8–3/2–11/7–11/6 \\ 1–12/11–15/11–3/2–18/11–21/11 [/math]

Each version excellently spans a full octave.

With undecimal chords figured out, tridecimal chords should be very easy. This time, consider the following subset tetrads in the upper segment first. This is the standard form of the tridecimal tetrad. Named the tridecimal micromajor semiquartal tetrad and the tridecimal microminor semiquartal tetrad, the two versions are

[math]\displaystyle 1–13/8–13/7–3 \\ 1–21/13–24/13–3 [/math]

Totally analogous to the undecimal chords, 13/8 constrasts to 21/13 and 13/7 constrasts to 24/13, both by 169/168, the buzurgisma. So we see how the 13th harmonic contributes to microtonality just as well.

Next, consider the following subset tetrads in the lower segment. This is the alternative form of the tridecimal tetrad. Named the tridecimal micromajor tetrad and the tridecimal microminor tetrad, the two versions are

[math]\displaystyle 1–13/12–13/10–3/2 \\ 1–15/13–18/13–3/2 [/math]

The micromajor is said for 13/12 as opposed to 14/13, and the microminor is said for 18/13 as opposed to 39/28.

Again, we concatenate them to obtain the extended form. Named the tridecimal micromajor chord and the tridecimal microminor chord, the two versions are

[math]\displaystyle 1–13/12–13/10–3/2–13/8–13/7 \\ 1–15/13–18/13–3/2–21/13–24/13 [/math]

Each version excellently spans a full octave.

Now, the classical chords i.e. the 5/ and /5 series shall be introduced.

Like the rooted one, the compact voicing has four segments spanning two octaves. Named the classical major chord and the classical minor chord, the two versions are

[math]\displaystyle 1–5/4–3/2–30/17–30/13–30/11–10/3–15/4 \\ 1–6/5–3/2–17/10–11/5–13/5–16/5–18/5 [/math]

It similarly has a supercompact voicing, whose two versions are

[math]\displaystyle 1–15/13–5/4–15/11–3/2–5/3–30/17–15/8 \\ 1–11/10–6/5–13/10–3/2–8/5–17/10–9/5 [/math]

Perhaps contrary to a community percept, the 5/ chord is the major chord, because the purpose of the entire chord is to demonstrate the presence of the otonal-5. Vice versa, the /5 chord is the minor chord.

The first segment is clearly identical to that of the rooted chord. Therefore, the just major/minor triad is also called the classical major/minor triad.

The second segment is more interesting. Not only does it sound a little strange when used in place of the just semiquartal segment, its very existence is a mystery. Named the classical pseudominor semiquartal triad and the classical pseudomajor semiquartal triad, the two versions are

[math]\displaystyle 1–30/17–3 \\ 1–17/10–3 [/math]

At the beginning of the second octave, the third segment is characterized by undecimal and tridecimal intervals. Named the classical microminor tetrad and the classical micromajor tetrad, the two versions are

[math]\displaystyle 1–15/13–15/11–3/2 \\ 1–11/10–13/10–3/2 [/math]

Finally, the fourth segment is very similar to that of the just chords, taken by two pairs of tones distributed quite homogeneously: 5/3 vs 8/5 and 15/8 vs 9/5, with 15/8 inverting to 8/5 and 5/3 inverting to 9/5. 1–5/4–3/2–15/8 is the major seventh chord. 1–6/5–3/2–9/5 is the minor seventh chord. 1–5/4–3/2–5/3 is the major sixth chord. 1–6/5–3/2–8/5 is the minor sixth chord. One should be very familiar with all of those. But one could also use the classical major semiquartal tetrad and the classical minor semiquartal tetrad, which are

[math]\displaystyle 1–5/3–15/8–3 \\ 1–8/5–9/5–3 [/math]

Where is 7/5? One may wonder. The answer is, it is not part of the standard series. Being a subdiminished fifth, 7/5 is repelled by 3/2. Using 7/5 in place of 3/2 yields a diminished chord, which will be discussed in the next chapter. 19/5 is repelled by the formal root. As for 21 and 23, one must incorporate an even higher odd limit so as to properly make use of them in the 5/ and /5 series.

As introduced above, superposing the first and the third segment produces a supercompact lower segment. This is the classical major–microminor pentad; its negative version is the classical minor–micromajor pentad. The two versions are

[math]\displaystyle 1–15/13–5/4–15/11–3/2 \\ 1–11/10–6/5–13/10–3/2 [/math]

Superposing the second and the fourth segment produces a supercompact upper segment. This is the classical major–pseudominor semiquartal pentad; its negative version is the classical minor–pseudomajor semiquartal pentad. The two versions are

[math]\displaystyle 1–5/3–30/17–15/8–3 \\ 1–8/5–17/10–9/5–3 [/math]

The septimal chords, i.e. the 7/ and /7 series are as complex. Fortunately, what happens here is totally analogous to the classical chords, so we should be ready.

Like the rooted and classical ones, the compact voicing has four segments spanning two octaves. Named the septimal major chord and the septimal minor chord, the two versions are

[math]\displaystyle 1–21/17–3/2–7/4–7/3–21/8–42/13–42/11 \\ 1–17/14–3/2–12/7–16/7–18/7–22/7–26/7 [/math]

It similarly has a supercompact voicing, whose two versions are

[math]\displaystyle 1–7/6–21/17–21/16–3/2–21/13–7/4–21/11 \\ 1–8/7–17/14–9/7–3/2–11/7–12/7–13/7 [/math]

It could never be overemphasised that the 7/ chord is the major chord, and the /7 chord is the minor chord.

This time, the second segment is identical to that of the rooted chord. Therefore, the just major/minor semiquartal triad is also called the septimal major/minor semiquartal triad.

Let us extract the strange first segment. This is analogous to the second segment in the classical chord. Named the septimal pseudominor triad and the septimal pseudomajor triad, the two versions are

[math]\displaystyle 1–21/17–3/2 \\ 1–17/14–3/2 [/math]

At the beginning of the second octave, comes the third segment, featuring the two homogeneously distributed tones – it is a septimal chord, after all. Named the septimal major tetrad and the septimal minor tetrad, the two versions are

[math]\displaystyle 1–7/6–21/16–3/2 \\ 1–8/7–9/7–3/2 [/math]

Finally, the fourth segment is characterized by undecimal and tridecimal intervals. Named the septimal microminor semiquartal tetrad and the septimal micromajor semiquartal tetrad, they are

[math]\displaystyle 1–21/13–21/11–3 \\ 1–11/7–13/7–3 [/math]

As introduced above, superposing the first and the third segment produces a supercompact lower segment. This is the septimal major–pseudominor pentad; its negative version is the septimal minor–pseudomajor pentad. The two versions are

[math]\displaystyle 1–7/6–21/17–21/16–3/2 \\ 1–8/7–17/14–9/7–3/2 [/math]

Superposing the second and the fourth segment produces a supercompact upper segment. This is the septimal major–microminor semiquartal pentad; its negative version is the septimal minor–micromajor semiquartal pentad. The two versions are

[math]\displaystyle 1–21/13–7/4–21/11–3 \\ 1–11/7–12/7–13/7–3 [/math]

That covers the basic nonrooted chords.

At this point, a bonus comes as the septendecimal pseudomajor sixth chord; its negative version is the septendecimal pseudominor seventh chord. The two versions are

[math]\displaystyle 1–17/14–3/2–17/10 \\ 1–21/17–3/2–30/17 [/math]

They function just like the harmonic sixth chord and the harmonic seventh chord, respectively, but they render colors that are completely deviant. They are the only septendecimal or undevicesimal chords that follow tertian–semiquartal harmony and are neither diminished nor augmented. Speaking of diminished and augmented, let us head to the next chapter.

Chapter IV. Diminished Chords and Augmented Chords

Diminished and augmented chords are categories of their own because they are puzzle pieces of distinct shapes. All concordant diminished or augmented chords are nonrooted. Instead, the most notable concordant diminished fifth is septendecimal, and it lends itself to the septendecimal chords, i.e. the 17/ and /17 series. The most notable concordant augmented fifth is undevicesimal, and it lends itself to the undevicesimal chords, i.e. the 19/ and /19 series.

These harmonics are characterized by pseudoambitonality. It describes the condition that 17/16 acts as both the augmented unison and the minor second, and that 19/16 acts as both the augmented second and the minor third. The consequence is, when it comes to diminished and augmented chords, both 17/12 and 24/17 can be used as the diminished fifth, and both 19/12 and 30/19 can be used as the augmented fifth. Two layers of tonality are abstracted. First, the pseudotonality, comprising pseudomajor and pseudominor, which describes explicit otonal and utonal intervals taking categories akin to classical ones. Second, the pseudomicrotonality, comprising pseudomicromajor and pseudomicrominor, which describes explicit otonal and utonal intervals sharing the same category.

Interval Category Characteristics	Layers of Tonality	Examples of Contrasting Ratios
Pivotal harmonics	Tonality	5/4 vs 6/5
Ambitonal harmonics	Microtonality	11/10 vs 12/11
Pseudoambitonal harmonics	Pseudotonality	30/17 vs 17/10
	Pseudomicrotonality	17/16 vs 18/17

The flexibility of these chords can be surprisingly high. First of all, there are the septendecimal pseudomajor diminished triad and the septendecimal pseudominor diminished triad:

[math]\displaystyle 1–17/14–17/12 \\ 1–20/17–24/17 [/math]

In the upper segment, there are the septendecimal pseudomajor diminished semiquartal triad and the septendecimal pseudominor diminished semiquartal triad:

[math]\displaystyle 1–17/10–17/6 \\ 1–28/17–48/17 [/math]

In either pair, the members are not inverses of each other. Unlike in the case of the standard series of chords, any inverse of the diminished chord is a rotation of a diminished chord in the other segment. There are

[math]\displaystyle 1–7/6–17/12 \\ 1–6/5–24/17 [/math]

One can verify those are rotations of the semiquartal triads. In addition, there are

[math]\displaystyle 1–5/3–17/6 \\ 1–12/7–48/17 [/math]

One can verify those are rotations of the tertian triads.

The semiquartal construction will be difficult to notate on a diatonic staff because the diminished twelfths in semiquartal construction are technically augmented elevenths, formed by a stack of two major sixths. Treating them as rotations of tertian triads solves the problem to a certain extent, but an enharmonic respelling accidental (i.e. Pythagorean comma accidental) is more advisable.

In the context of comparing the inverses, the expanded name of the septendecimal pseudomajor diminished triad is the septendecimal pseudomajor–pseudomicromajor diminished triad, which shares the diminished fifth of 17/12 with its inverse, the septendecimal pseudominor–pseudomicromajor diminished triad. They have the thirds displaced by 51/49, whose size is very close to 25/24. Besides, the expanded name of the septendecimal pseudominor diminished triad is the septendecimal pseudominor–pseudomicrominor diminished triad, which shares the diminished fifth of 24/17 with its inverse, the septendecimal pseudomajor–pseudomicrominor diminished triad. They have the thirds displaced by 51/50, whose size is very close to 49/48. The same chromas also appear in semiquartal forms. That reveals the similarity between pseudotonality and pivotal tonality. Furthermore, the diminished fifths are displaced by 289/288, analogous to 121/120 and 169/168. That reveals the similarity between pseudomicrotonality and microtonality.

Concatenating the segments gives us diminished seventh/sixth chords, the septendecimal pseudomajor diminished sixth chord and the septendecimal pseudominor diminished seventh chord:

[math]\displaystyle 1–17/14–17/12–17/10 \\ 1–20/17–24/17–28/17 [/math]

It should be noted that all their rotations are still diminished chords. Not only are there chords that retain the septendecimal tritones:

[math]\displaystyle 1–7/6–17/12–5/3 \\ 1–6/5–24/17–12/7 [/math]

but also chords characterized by the subdiminished fifth of 7/5 and the superaugmented fourth of 10/7:

[math]\displaystyle 1–7/6–7/5–28/17 \\ 1–6/5–7/5–17/10 \\ 1–20/17–10/7–12/7 \\ 1–17/14–10/7–5/3 [/math]

The augmented chords are way simpler. The undevicesimal pseudomajor augmented triad and the undevicesimal pseudominor augmented triad are

[math]\displaystyle 1–19/15–19/12 \\ 1–24/19–30/19 [/math]

whose inverses are rotations of the original chords. The three intervals involved in building any of them are always 5/4, 24/19, and 19/15.

Chapter V. Things Repel the Similar but Not Identical

This chapter is dedicated to chord progressions. Most common chord progressions in meantone hardly work in JI. For example, in the vi–ii–V–I progression, all the roots make up an essentially tempered chord of meantone. A similar progression is I–ii–V–I, featured in the first four bars of BWV 846 Prelude in C Major.

Figure 5: BWV 846 b. 1–4

One notorious JI redux, given by the official FJS document, is as follows.

Figure 6: official FJS rendition of BWV 846 b. 1–4

In the rendition, every individual chord is chosen to be concordant, but there is a bump between the second and the third chord without an actual melodic function. An alternative would involve accepting an extremely disturbing wolf fifth, which cannot be worse in such supposedly euphonious harmonic context, though appropriate usage under conditions like well supported harmony, quick passing tones or ornaments is possible.

From a historical perspective, meantone was discovered for a good reason. Letting it do its duty is of the greatest mercy. Not accounting for the discordance of wolf fifths or melodic bumps is equivalent to holding that meantone need not exist, and that most recent to modern theories are either failure or flukes based on wrong principles.

In functional harmony analysis, we say the subdominant function and the secondary dominant function are unified in meantone, but they are distinct in JI and different by a comma. The subdominant function is normally a IV chord rooted on 4/3 relative to tonic, but ii can be used in place as it is the parallel minor chord of IV – it is best named IV6. Since tonic is to subdominant what dominant is to tonic, the tonic–subdominant progression is strong and smooth. The secondary dominant function is usually understood as V/V i.e. II, but perhaps less obviously, v/V also has this function. After all, ii–V–I did not arise out of nowhere: Schoenberg identified fifth descension as the ultimate source of the dominant function. Consequently, both subdominant and secondary dominant are emergent in ii in the progression of I–ii–V–I. I–ii is tonic–subdominant, while ii–V is secondary dominant–dominant. In terms of ratios, the subdominant ii chord is 10/9–4/3–5/3 relative to the tonic, where 4/3 and 5/3 are the root and the third of IV, and 10/9 is derived as a fifth below 5/3. The secondary dominant ii chord is 9/8–27/20–27/16 relative to the tonic, where 9/8 is the fifth of V and the other notes are built on it. They are separated exactly by a comma, and the only way to use a ii chord with both functions to connect to both sides is to temper it out.

If the comma is not tempered out, the progression does not hold. The idea to force it is absurd. Fitting one function will leave the other emergent function misplaced by a comma, which is easily the most catastrophic scene in the world – the uncanny valley of harmony. I have put it into my favorite verse:

Verse

Things repel the similar but not identical.

This principle guides us to authentic JI progressions, but it must be emphasised that the implication is the avoidance of progressions which involve a wolf fifth, whereas commatic contrasts can still be reasonably exploited in the melody. The wolf fifth is defined as an interval which is inambiguously mapped to 14\24 by 24et. Semiambitonal intervals such as 32/21 are, of course, not wolf fifths.

As an immediate achievement, I–ii is ruled out as a JI progression whenever the I involves the third of 5/4 or the ii involves the third of 6/5, because (1) the bare fifths of I-ii make up a chain of 1-3/2-9/8-27/16; (2) the third of 5/4 in I is a wolf fifth above 27/16; and (3) the third of 6/5 in ii is a wolf fifth below the tonic. It can be stated as the whole tone progression rule:

Whole tone progression rule

A chord involving the major third of 5/4 must not be followed by a chord rooted on its supertonic;

A chord involving the minor third of 6/5 must not be followed by a chord rooted on its subtonic.

Figure 7: I–ii making up a long chain of fifths

Now, we see a lot of things that do not work. Do we know anything that works? Sure. We know dominant–tonic works. V–I is gold. We know tonic–subdominant works. I–IV is gold. Subdominant–dominant works with some quirks. Specifically, IV–V is like I–ii, where the IV must not take a third of 5/4. This way, I–IV–V–I will be totally fine. Here is a possible redux of BWV 846 b. 1–4. See Appendix D for another solution.

Figure 8: Flora's rendition of BWV 846 b. 1–4

Its reverse is I–V–IV–I. Does it work either? Absolutely. V–IV is a nontrivially different sound, with a distinct musical feeling. The fact that they are nontrivially different is an argument for their viability, not against.

Problem is, most common chord progressions are open progressions that loop over in four bars. In the rest of this chapter, we will discuss the JI versions of the following notable examples: I–V–vi–IV, i–VI–III–VII, vi–ii–V–I, and VI–VII–v–i.

Let us begin by fitting one additional chord between IV and V. I–IV–vi–V can work, though it is somewhat limited. The vi is required by vi–V to be rooted on 27/16. Hence, itself must avoid 6/5, and both the IV and the V must avoid 5/4. That basically makes it a nonclassical progression. For an alternative, we should find out the function of the vi: sometimes known as tonic–subdominant (TS), or equivalently, submediant. Either mediant or antitonic would be a proper replacement.

Using mediant, it is I–IV–iii–V, and its reverse is I–V–iii–IV. Antitonic gives a more sophisticated sound. First noted by Aura, this function is rooted on the pitch which is a tritone from the tonic. In this case we should use #IV, so the progression is I–IV–#IV–V. This #IV can be rooted on various ratios, such as Ptolemaic (45/32), Alpharabian (363/256), Pythagorean (729/512) or even sqrt (2), depending on context and the desired effect. Does its reverse work? Well, by convention, semitone progressions like this should be a chromatic semitone followed by a diatonic semitone. When it is placed backwards, we should use bV instead. I–V–bV–IV is a good answer.

Moving on to the next progression, i–VI–III–VII is the minor counterpart of I–V–vi–IV. They are the same progression but rotated by two bars, with a natural consequence of re-establishing the tonic. As discussed, itself works as a nonclassical progression. In addition, i–VI–III–v can be used, with v, the dominant, substituting for VII, the subtonic.

vi–ii–V–I is the most tricky. The only way to tame this consecutive descension of perfect fifths is to omit the 6/5 in vi and the 5/4 in I, and I–vi would involve going down by 32/27. This is very limited. For an alternative, we must decide whether we want the ii to be subdominant or secondary dominant as analysed before. As subdominant, it is IV6 already, so a nonclassical IV can be substituted, thus vi–IV–V–I. As secondary dominant, v/V can be left unchanged, and a nonclassical IV can replace vi, thus IV–ii–V–I. Other viable options include mediant, vi–iii–V–I, lead, vi–vii–V–I, antitonic, vi–#IV–V–I, and submediant, vi–bVI–V–I.

VI–VII–v–i is in a sense the minor counterpart of vi–ii–V–I. Fortunately, it already has the ii replaced by VII, so it works out of the box as long as the VI does not contain 5/4.

Chapter VI. Overview on Functional Harmony

A substantial portion of the previous discussion is about harmonic functions. To see a bigger picture, this chapter systematically explains all functions in positive harmony, with those in negative harmony developed analogously. Heavily inspired by Aura's Ideas on Functional Harmony, this system resembles it in a lot of ways. The main differences are terminology and the level of abstraction. It is more abstract as it takes full advantage of regular temperament theory, and short-circuits the debate on the concrete boundary of each category. The figure below is an overview.

Figure 9: Flora's function map

Explicit Functions

This part draws inspiration from the two mainstream schools of thought regarding diatonic functional harmony – the German theory pioneered by Hugo Riemann, and the Viennese theory developed by Sechter, Schoenberg, Schenker and others.

Derivation from German Theory

In the German theory, three tonal functions are abstracted as tonic, dominant, and subdominant, equipped with operations to derive composite diatonic functions.

Aura has renamed subdominant to serviant, which happens to start with an s too. The system introduced here does not adopt that for fear of confusion. As part of the classical narrative, dominant is not to be taken literally as the governing entity. In fact, the root is the cause of the fifth; the root governs the fifth. So the fifth is the governed entity. However, Aura's metaphors of dominant and serviant are not only told with respect to tonic. They form a distinct narrative leading to a novel path.

Because these functions are so pivotal, rational variation cannot be allowed. Tonic is precisely 1/1; other ratios tempered out by 7et are chromatic, precisely tonic chromatic. Tonic and chromatic can be collectively dubbed tonic/chromatic. The same applies to dominant and subdominant. Fifths (4\7) that are not 3/2 are dominant chromatic. Fourths (3\7) that are not 4/3 are subdominant chromatic. They are collectively dubbed dominant/chromatic and subdominant/chromatic, respectively.

These chromatic ratios never take diatonic functions, but can take chromatic functions, discussed further below.

Derivation from Viennese Theory

The Viennese theory originally focused on how each diatonic degree related to the tonic, but those were recognized as functions later. Hence, the rest of the diatonic functions are supplied: mediant, for the function of thirds (2\7); submediant, of sixths (5\7); vicinant, of seconds (1\7); and subvicinant, of sevenths (6\7).

These functions are subject to a good amount of rational variation – each is bound by a range spanned by the minor category to the major category, and ratios falling out of the bound do not qualify for bearing the function. For instance, 8/5, 18/11 and 5/3 all fall into the range of minor to major sixth, and thus all are submediant. 192/125, being a diminished sixth, cannot be said to be submediant, but submediant chromatic.

In general, tonic, vicinant, mediant, subdominant, dominant, submediant, and subvicinant accommodate ratios mapped to perfect unison (0\7, 0\24), minor to major second (1\7, 2\24–4\24), minor to major third (2\7, 6\24–8\24), perfect fourth (3\7, 10\24), perfect fifth (4\7, 14\24), minor to major sixth (5\7, 16\24–18\24), and minor to major seventh (6\7, 20\24–22\24), respectively.

Chromatic Functions

Unlike the diatonic functions introduced before, chromatic functions are defined by chromatic steps, sometimes overlaid on the diatonic functions. These include the three commatic functions, lead, and antitonic.

Ratios that are not 1/1 but are tempered out by 24et are commatic, precisely tonic commatic. Those mapped to 14\24 that are not 3/2 are dominant commatic. Those mapped to 10\24 that are not 4/3 are subdominant commatic. All commatic ratios are harmonically repelled alike.

Ratios mapped to 2\24 or 22\24 are what people call leading tones, whose corresponding function is lead. It does not matter whether it approaches the tonic from above or from below, but modifiers such as upper or lower may be added if necessary. It has two diatonic subtypes – the one mapped to 1\7 or 6\7 wants to resolve to tonic, called collocant, and the one mapped to 0\7 or 7\7 wants to get away from tonic, called dislocant. That leaves major seconds (1\7, 4\24) and minor sevenths (6\7, 20\24) out, and as one may expect, they are called supertonic and subtonic, respectively. From here, seconds are divided into collocant and supertonic, and sevenths are divided into subtonic and collocant. Such distinction is made mainly based on the observation of the unique tonal tension in leading tones.

Antitonic accommodates ratios mapped to 12\24. This is another chromatic function consisting of two diatonic subtypes – the augmented fourth, mapped to 3\7, and the diminished fifth, mapped to 4\7. Aura has named the two subtypes sycophant and tyrant, respectively. This function is versatile as it is to subdominant or dominant what lead is to tonic, so it tends to resolve to either subdominant or dominant. Strong effects are easily achieved through this function.

Aura has crafted some vivid explanations for the naming of the subtypes. On sycophant:

[It has] this tendency to "kiss up to" and tonicize the dominant.

On tyrant:

It tends to contrast with the tonic in a manner somewhat akin to that of a dominant, but by sheer brute force and contrary harmonic nature.

Implicit Functions

This part is what Aura calls paradiatonic functions for those in the gap of the diatonic and chromatic scheme.

Varicant and Subvaricant

Varicant lies roughly in the middle of the tonic and the dominant one octave above. Intervals in this region are more appropriately described as hemitwelfths than as sixths or sevenths.

While the concept is easy to understand given the amount of discussion dedicated to hemitwelfths, the boundaries of these functions can be less intuitive, detailed later. For now, let us just say ratios mapped to 19\24 are varicant, and those mapped to 5\24 are subvaricant.

Aura has used contravaricant in place of subvaricant.

Covaricant and Subcovaricant

Covaricant is on the other side of mediant, and subcovaricant is on the other side of submediant. Ratios mapped to 15\24 are covaricant, and those mapped to 9\24 are subcovaricant.

These two functions correspond to Aura's superobstant and subobstant, respectively.

Duplicant and Subduplicant

Mapped to 11\24, duplicant manifests itself as a sort of double mediant – since the primary subdivision gives mediant, the secondary subdivision gives double mediant. Subduplicant is accordingly the function of ratios mapped to 13\24.

These two functions correspond to Aura's intersubiant and interregnant, respectively.

Coduplicant and Subcoduplicant

While duplicant is the mediant of mediant and dominant, coduplicant is the mediant of tonic and mediant. Subcoduplicant is to coduplicant what subduplicant is to duplicant. Further detailing on the second and the seventh, ratios mapped to 3\24 are coduplicant, and those mapped to 21\24 are subcoduplicant.

These two functions correspond to Aura's superabrogant and subabrogant, respectively.

Gradient

Gradient is the function of quartertones.

Another candidate term for this function is dietic. However, given that the interval category scheme is based on 24et, the "dietic" function cannot arise because both the 3-limit diesis (Pythagorean comma, 531441/524288) and the 5-limit diesis (augmented comma, 128/125) are tempered out.

The quartertone is not a diesis. Melodically, the diesis can be used to refer to the smallest melodic unit, and that may be either a quartertone or a comma. Harmonically, the diesis is commatic in nature, whereas quartertones are more useful. In particular, a just major tetrad built on V features 33/32, which resolves marvelously to tonic.

Composite Functions

Due to semiambitonality, intervals mapped across two adjacent functions will take on both even in a fixed harmonic context, breeding a richer variety of harmonic gestures.

Bleed

Bleed is the composite of gradient and lead for ratios mapped to 1\24 and 2\24, or to 23\24 and 22\24. This composition of functions is what makes it much stronger than lead alone.

Counterbleed

Counterbleed is the composite of coduplicant and lead for ratios mapped to 3\24 and 2\24, or of subcoduplicant and lead for those mapped to 21\24 and 22\24. It has a similarly strong effect as bleed, but it is unique in that it achieves a strange equilibrium – the tendency to resolve to tonic or to supertonic or subtonic are about equal due to tonic having greater gravity than supertonic or subtonic.

Dominant Bleed and Subdominant Bleed

Dominant bleed is the composite of subduplicant and antitonic for ratios mapped to 13\24 and 12\24, and subdominant bleed is the composite of duplicant and antitonic for ratios mapped to 11\24 and 12\24. In either case, it has asymmetrical relations to dominant and to subdominant, resulting in more active characters than pure antitonic.

Supercommatic and Subcommatic

Supercommatic is the composite of commatic and gradient. Subcommatic is supercommatic on the opposite side. Because commatic is part of their nature, these functions are harmonically repelled like pure commatic ratios.

Countersubcommatic and Countersupercommatic

Countersubcommatic is the composite of coduplicant and supertonic. Countersupercommatic is the composite of subcoduplicant and subtonic. These functions can be harmonically useful.

Dominant Subcommatic and Subdominant Supercommatic

Dominant subcommatic is the composite of dominant commatic and subduplicant. Subdominant supercommatic is the composite of subdominant commatic and duplicant. These functions are harmonically repelled like pure commatic ratios.

Composite Function Rule

All that are left are the composites involving varicant, subvaricant, covaricant, and subcovaricant. There is the composite function rule:

Composite function rule

Composite involving varicant is varicant;

Composite involving subvaricant is subvaricant;

Composite involving covaricant is covaricant;

Composite involving subcovaricant is subcovaricant.

In other words, if a semiambitonal ratio can be associated with varicant, subvaricant, covaricant or subcovaricant, it is. The rule defines the boundaries of the varicant-like functions for the system to make the most sense. For example, the resultant functions of septimal intervals are as follows:

Harmonic Functions of Septimal Intervals

Ratios	Functions
8/7, 7/6	Subvaricant
9/7, 21/16	Subcovaricant
32/21, 14/9	Covaricant
7/4, 12/7	Varicant

It reflects the knowledge that 21/16 is not a wolf fourth and that 32/21 is not a wolf fifth. Rather, it affirms they are representative of fine melodic contours with decent harmonic gestures.

Chapter VII. Overview on Microtempering

The relevance of the tempered scene is supported by the fact that the harmonic identities of intervals need not be harmed by tempering. Strict monotonicity is key to preserving harmonic identities. If two intervals are conflated or swapped in size, their original identities are lost. Strict monotonicity is arguably one of many good criteria for microtempering.

With tempering comes essentially tempered chords. Despite the name, they are better off as root progressions than as chords, because most of them are either not invertible or leading to enormous errors. There are a handful of exceptions. Perhaps the island chords are the most versatile of all.

Tempering out the island comma, 676/675, will introduce an exact hemitwelfth that directly constitutes the essentially tempered chord. It is

[math]\displaystyle \operatorname {(Island)} 1–26/15–3 [/math]

Perfect voicing in the lower segment follows immediately, as

[math]\displaystyle \operatorname {(Island)} 1–15/13–4/3–3/2 \\ \operatorname {(Island)} 1–9/8–13/10–3/2 \\ \operatorname {(Island)} 1–15/13–13/10–3/2 [/math]

The first two tetrads are inverses of each other. The third is perfectly symmetric. All of them can be concatenated with the upper-segment triad.

Within 21-odd-limit strict monotonicity, other notable nullity-1 essentially tempered chords are xenismic (2058/2057), ramanujanismic (1729/1728), nicolic (1575/1573), quadrantonismic (1156/1155), gamelismic (1029/1024), swetismic (540/539), boethius (513/512), minor minthmic (364/363), keenanismic (385/384), marveltwin (325/324), major minthmic (352/351), and rastmic (243/242). See Appendix A for a list.

Island tempering seems to be the most elegant way to introduce an exact hemitwelfth. Together with the sinaisma we obtain {676/675, 1001/1000}. Not tempering out the island comma and preserving the exact hemitwelfth will make the island comma tuned to an even number of steps, which may be too complex for any human being to grasp.

As for other quadratic irrationals, temperaments may offer a semioctave, a hemitwelfth, or a neutral third simply by tempering JI. As the neutral third is the difference between the hemitwelfth and the semioctave, they are not independent. In fact, a temperament either hits all, or misses two out of the three.

Introduced in the Previous Episode, kalismic tempering offers a semioctave. We also note that breedsmic tempering offers a neutral third. The greenland temperament {676/675, 1001/1000, 1716/1715} tempers out the kalisma, the island comma, and the breedsma, so it boasts the semioctave, the hemitwelfth, and the neutral third. Supported by 270et, it is one of the best quadratic irrational microtemperament in the 13-limit.

If we take 224et as dual to 270et due to their opposite tuning profiles, 224et is found to hit the semioctave but miss the hemitwelfth. That implies a dual rank-3 temperament to greenland which is also found to hit the semioctave but miss the hemitwelfth – the hades temperament {540/539, 729/728, 1575/1573}. Like in 270et, greenland tunes harmonics 11 and 13 secretly flat, while hades tunes them secretly sharp. They unite to the harry temperament, an extremely important rank-2 temperament in the 13-limit. Another potential dual to 270et is 311et, which hits the neutral third but misses both the semioctave and the hemitwelfth. Which one makes more sense as a dual depends on the perspectives. The corresponding rank-3 temperament is more complex, {1575/1573, 2080/2079, 2401/2400}.

Appendix A. List of Essentially Tempered Chords

Island essentially tempered

Lower segment

[math]\displaystyle \operatorname {(Island)} 1–15/13–4/3–3/2 \\ \operatorname {(Island)} 1–9/8–13/10–3/2 \\ \operatorname {(Island)} 1–15/13–13/10–3/2 [/math]

Upper segment

[math]\displaystyle \operatorname {(Island)} 1–26/15–3 [/math]

Extended

[math]\displaystyle \operatorname {(Island)} 1–15/13–4/3–3/2–26/15 \\ \operatorname {(Island)} 1–9/8–13/10–3/2–26/15 \\ \operatorname {(Island)} 1–15/13–13/10–3/2–26/15 [/math]

Xenismic essentially tempered

[math]\displaystyle \operatorname {(Xenismic)} 1–11/7–21/11–3[/math]

Ramanujanismic essentially tempered

Lower segment

[math]\displaystyle \operatorname {(Ramanujanismic)} 1–19/16–9/7–3/2 \\ \operatorname {(Ramanujanismic)} 1–7/6–24/19–3/2 [/math]

Upper segment

[math]\displaystyle \operatorname {(Ramanujanismic)} 1–13/8–36/19–3 \\ \operatorname {(Ramanujanismic)} 1–19/12–24/13–3 [/math]

Nicolic essentially tempered

[math]\displaystyle \operatorname {(Nicolic)} 1–11/10–15/11–3/2 [/math]

Quadrantonismic essentially tempered

[math]\displaystyle \operatorname {(Quadrantonismic)} 1–17/14–3/2–30/17 \\ \operatorname {(Quadrantonismic)} 1–21/17–3/2–17/10 [/math]

Gamelismic essentially tempered

[math]\displaystyle \operatorname {(Gamelismic)} 1–8/7–21/16–3/2 [/math]

Swetismic essentially tempered

[math]\displaystyle \operatorname {(Swetismic)} 1–7/6–15/11–3/2 \\ \operatorname {(Swetismic)} 1–11/10–9/7–3/2 \\ \operatorname {(Swetismic)} 1–7/6–9/7–3/2 [/math]

Boethius essentially tempered

[math]\displaystyle \operatorname {(Boethius)} 1–19/16–4/3–3/2 \\ \operatorname {(Boethius)} 1–9/8–24/19–3/2 \\ \operatorname {(Boethius)} 1–9/8–4/3–3/2 [/math]

Minor minthmic essentially tempered

[math]\displaystyle \operatorname {(Minor\ minthmic)} 1–13/11–14/11–3/2 [/math]

Keenanismic essentially tempered

Lower segment

[math]\displaystyle \operatorname {(Keenanismic)} 1–6/5–21/16–3/2 \\ \operatorname {(Keenanismic)} 1–8/7–5/4–3/2 [/math]

Upper segment

[math]\displaystyle \operatorname {(Keenanismic)} 1–12/7–15/8–3 \\ \operatorname {(Keenanismic)} 1–8/5–7/4–3 [/math]

Extended

[math]\displaystyle \operatorname {(Keenanismic)} 1–6/5–21/16–3/2–8/5–7/4 \\ \operatorname {(Keenanismic)} 1–8/7–5/4–3/2–12/7–15/8 [/math]

Marveltwin essentially tempered

[math]\displaystyle \operatorname {(Marveltwin)} 1–5/3–24/13–3 \\ \operatorname {(Marveltwin)} 1–13/8–9/5–3 \\ \operatorname {(Marveltwin)} 1–5/3–9/5–3 [/math]

Major minthmic essentially tempered

Lower segment

[math]\displaystyle \operatorname {(Major\ minthmic)} 1–11/9–3/2 \\ \operatorname {(Major\ minthmic)} 1–16/13–3/2 \\ \operatorname {(Major\ minthmic)} 1–9/8–4/3–3/2 [/math]

Upper segment

[math]\displaystyle \operatorname {(Major\ minthmic)} 1–16/9–3 \\ \operatorname {(Major\ minthmic)} 1–22/13–3 \\ \operatorname {(Major\ minthmic)} 1–13/8–11/6–3 \\ \operatorname {(Major\ minthmic)} 1–18/11–24/13–3 [/math]

Extended

[math]\displaystyle \operatorname {(Major\ minthmic)} 1–11/9–3/2–16/9 \\ \operatorname {(Major\ minthmic)} 1–11/9–3/2–22/13 \\ \operatorname {(Major\ minthmic)} 1–16/13–3/2–16/9 \\ \operatorname {(Major\ minthmic)} 1–16/13–3/2–22/13 \\ \operatorname {(Major\ minthmic)} 1–11/9–3/2–13/8–11/6–9/4–8/3 \\ \operatorname {(Major\ minthmic)} 1–16/13–3/2–18/11–24/13–9/4–8/3 [/math]

Rastmic essentially tempered

[math]\displaystyle \operatorname {(Rastmic)} 1–11/9–3/2 [/math]

Appendix B. Revelation of Harmonic Identities

Any interval subject to harmonic use must have a harmonic identity, though its revelation in the sea of harmonic entropy is often conditional. It has to do with the audience's capacity to get impressed by the material, so as to recognize, and most importantly, relate to the material.

With respect to the level at which harmonics reveal themselves, harmonics may be split into three categories: proximal, medial, and distal. Those are the same terms as in Aura's Ideas of Consonance, where Aura has adopted a similar criteria based on timbral fusion between pitches and emergence of the virtual fundamental.

Proximal harmonics range from 1 to 24. All of these harmonics have clear harmonic functions, and they participate construction of chords with clarity in terms of harmonic intent.

Medial harmonics start at 25, and end at 576. The 25th harmonic is mapped to 16\24, so the only candidate harmonic function would be submediant, like 8/5. Meanwhile, it is mapped to 4\7, so it cannot be submediant, making it the first harmonic without a clear harmonic function. As for what it sounds like, the identity of a mistuned 14/9 is more emergent than its supposed self. At the other end, 576 increments 575, and marks the difference between 25/24 and 24/23.

As medial harmonics are a forest of wolf intervals, they are supposed to work in well supported harmony, quick passing tones or ornaments. Attempt at wolf intervals with well supported harmony to bring its harsh sound under control may be dubbed wolf taming. This is a comprehensive practice, with contributing factors including but not limited to voicing, timbre, and dynamics. A reliable panacea is unlikely to exist due to its heuristic nature.

Distal harmonics start at 577. They are seldom worth the concern because they are located way too far from the root. For the record, said harmonic is more than nine octaves above the root.

Appendix C. Harmonic Identities of Individual Harmonics

First octave

• 2: perfect octave (tonic)

Second octave

• 3: perfect fifth (dominant)
• 4: perfect octave (tonic)

Third octave

• 5: major third (mediant)
• 6: perfect fifth (dominant)
• 7: subminor seventh (varicant)
• 8: perfect octave (tonic)

Fourth octave

• 9: major second (supertonic)
• 10: major third (mediant)
• 11: semiaugmented fourth (duplicant)
• 12: perfect fifth (dominant)
• 13: subneutral sixth (submediant)
• 14: subminor seventh (varicant)
• 15: major seventh (lead)
• 16: perfect octave (tonic)

Cut fifth octave

• 17: semitone (lead)
• 18: major second (supertonic)
• 19: sesquitone (mediant)
• 20: major third (mediant)
• 21: subfourth (subcovaricant)
• 22: semiaugmented fourth (duplicant)
• 23: subsemidiminished fifth (dominant bleed)
• 24: perfect fifth (dominant)

Appendix D. JI Redux of Prelude in C Major (BWV 846)

Despite its simplicity, arrangement of this work into JI proves difficult because it has had meantone logic so internalized. For the same reason, JI editions will inevitably sound somewhat forced without substantial revision, especially when compared to natively crafted JI pieces. Nonetheless, this edition chooses to keep all the note nominals, and no note deviates from the original work more than a quartertone.

This edition is notated in HEJI. In bar 14, the B is 32/17 above tonic, spelt with an enharmonic accidental.

• 
• 

Release Notes

© 2022–2024 Flora Canou

Version Stable 6 Beta 0

This work is licensed under the Creative Commons Attribution-ShareAlike 4.0 International License.