User:FloraC/Analysis on the 13-limit just intonation space: episode i
Preface
Just intonation is the repertoire of pitch materials that is the most concerning. In this essay, it refers to the infinite-dimensional harmonic space consisting of all rational numbers, sometimes dubbed as rational intonation.
It should take no effort to recognize the source of its significance, but making it clear will benefit. Just intonation is an elephant in the room – in that one cannot turn a deaf ear to it. Again, it matters to point it out that, analytically, inharmonicity is not the same as harmonicity, just like fractions are not the same as integers. Additions and multiplications in the harmonic space always result in something in the said space. In math, it is called a ring. Precisely, it demonstrates the following properties:
- The harmonic of a harmonic of a fundamental remains a harmonic of the original fundamental.
- The harmonic of a fundamental is a harmonic of another fundamental whose harmonic is the original fundamental.
They are inverses of each other: the first finds the harmonic series; the second finds the subharmonic series. The same cannot be said of arbitrary inharmonic spaces.
Of course, simply disregarding irrational intervals cannot be deemed just, as explained in my previous essay There Is Not a Third Side of the River, since the semioctave, for example, is a highly characteristic sound just as important as those rational intervals. These quadratic irrationals will be addressed in the later sections. It is an indispensible part of this analysis.
As for the artificial attempts where utterly irrelevant entities are forced together, like using π as frequency ratio of the sound, I have criticized in Fundamental Principles to Musical Sense and have no reason to discuss even further.
The 13-limit just intonation is of particular interest for multiple reasons. The structure is neat and cognitively accessible for homo sapiens, yet is sophisticated enough to breed rich harmonic gestures and tempering options. Each prime harmonic in this space has a relatively distinct identity, which unfolds fairly consistently, unlike higher primes.
This essay aims to be objective. Explanations on my favorite temperaments will not be present – at least not in sufficiency to single them out.
Now let us start with Pythagorean tuning aka 3-limit just intonation.
Chapter I. How Pythagoras Broke the Tuning
The Pythagorean tuning or 3-limit just intonation is the backbone of the interval space. My classification of Pythagorean intervals is exactly the same as Functional Just System (FJS), so I guess I should only cite it[1].
FJS technique #1: to convert from a Pythagorean ratio to an FJS representation
1. Factorize the ratio.
2. Initially ignore octaves (powers of two).
3. If the power of three is positive, move that many steps by fifths clockwise; if negative, move anticlockwise. Convert that number to an interval.
4. Adjust octaves as required.
Example: To convert 9/8 to the FJS, we factorize: 2-3 32. We ignore the factor of two. The power of three is +2, so we move two fifths clockwise: C–G–D. We have a major second. No octave adjustment needs to be made. The answer is M2.
FJS Technique #2: to convert from an FJS representation of a Pythagorean ratio back to the ratio.1. Initially ignore octaves.
2. Convert the interval to the number of steps by fifths, name it n.
3. Calculate red (3n)
4. Adjust octaves as required.
Example: To convert the FJS interval m3 to a Pythagorean ratio, we convert it first to -3 fifths: C–F–B♭–E♭. We now raise 3 to that power: 3-3. This is 1/27. To bring this number between 1 (inclusive) and 2 (exclusive), we multiply by 32 to get the answer: 32/27.
and
This is pretty boring for now.
This tuning naturally gives us the 7-tone diatonic scale and the 12-tone chromatic scale. Based on the diatonic scale, each interval is assigned a diatonic degree by the mapping of 7et:
[math]\displaystyle{ \langle \begin{matrix} 7 & 11 \end{matrix} ] }[/math]
Each degree changes its size through rotation. As such, each interval is assigned major or minor based on their size. Meanwhile, the chromatic scale can be generated this way (discarding either of the tritones), and implies the mapping of 12et:
[math]\displaystyle{ \displaystyle \langle \begin{matrix} 12 & 19 \end{matrix} ] }[/math]
Together, as is found out by Mike Battaglia, the change of basis
[math]\displaystyle{ \displaystyle \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \rightarrow \begin{bmatrix} 7 & 11 \\ 12 & 19 \end{bmatrix} }[/math]
is helpful for Pythagorean interval classification[2]. In particular, it is easy to identify the following tempered monzos:
[math]\displaystyle{ \displaystyle [ \begin{matrix} 1 & 1 \end{matrix} \rangle }[/math]
is a diatonic semitone, or limma for short. In this case it is 256/243. A movement by this would change the diatonic degree as well as the chromatic degree.
[math]\displaystyle{ \displaystyle [ \begin{matrix} 0 & 1 \end{matrix} \rangle }[/math]
is a chromatic semitone, or chroma for short. In this case it is 2187/2048. A movement by this does not change the diatonic degree but only the chromatic degree.
[math]\displaystyle{ \displaystyle [ \begin{matrix} 1 & 0 \end{matrix} \rangle }[/math]
is an enharmonic diesis. In this case it is the Pythagorean comma, 531441/524288. A movement by this changes the diatonic degree but not the chromatic degree.
It is possible to build tonality using the Pythagorean tuning, but the major and minor categories of intervals here are only to be understood in combination with diatonic degrees for the purpose of marking generator steps i.e. fifth shifts, and are not to be confused with the major and minor tonality. An interval is perfect if its number of generator steps is -1, 0, or +1, major if it is +2 to +5, and minor if it is -5 to -2.

Meantone tempers out 81/80, the syntonic comma, identifying 5/4 by 2 diatonic degrees and 4 generator steps. That is how 5/4 is called a major third.
5-limit just intonation can be analysed as the syntonic comma added to the Pythagorean tuning, or meantone with the syntonic comma recovered, represented by the following mapping:
[math]\displaystyle{ \displaystyle \begin{bmatrix} 7 & 11 & 16 \\ 12 & 19 & 28 \\ 0 & 0 & 1 \end{bmatrix} }[/math]
or in terms of generator steps:
[math]\displaystyle{ \displaystyle \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 4 \\ 0 & 0 & 1 \end{bmatrix} }[/math]
with the syntonic comma mapped to the tempered monzo of [0 0 -1⟩ in both cases. Since the first two entries are zero, this tempered monzo marks neither diatonic moves nor chromatic moves, but a commatic one, which only alters the color of the interval. A Pythagorean interval altered by the syntonic comma is dyed with the "color of 5". For example, 81/64 is M3, whereas 5/4 is M35. While both are members of major thirds, 5/4 involves otonal-5.
Now these are some of the diatonic semitones:
| Name[3] | Ratio | Monzo | Size (¢) | FJS |
|---|---|---|---|---|
| Large limma | 27/25 | [0 3 -2⟩ | 133.2 | m225 |
| Classical limma | 16/15 | [4 -1 -1⟩ | 111.7 | m25 |
| Pythagorean limma | 256/243 | [8 -5⟩ | 90.2 | m2 |
Each is separated by 81/80.
These are some of the chromatic semitones:
| Name | Ratio | Monzo | Size (¢) | FJS |
|---|---|---|---|---|
| Pythagorean chroma | 2187/2048 | [-11 7⟩ | 113.7 | A1 |
| Large chroma | 135/128 | [-7 3 1⟩ | 92.2 | A15 |
| Classical chroma | 25/24 | [-3 -1 2⟩ | 70.7 | A125 |
Each is separated by 81/80.
Chapter II. Septimal Voice Leading
81/80 translates a Pythagorean interval to a classical one. What is its septimal counterpart, which translates a Pythagorean interval to a septimal one? The answer is 64/63, the septimal comma.
Superpyth is the corresponding temperament of the septimal comma. It is the opposite of meantone in several ways. To send 81/80 to unison, meantone tunes the fifth flat. To send 64/63 to unison, superpyth tunes the fifth sharp. In septimal meantone, intervals of 5 are simpler than those of 7, whereas in septimal superpyth, intervals of 7 are simpler than those of 5, and their overall complexities are comparable. George Secor identified a few useful equal temperaments for meantone and superpyth. He noted 17, 22, and 27 to superpyth are what 12, 31, and 19 to meantone, respectively[4]. I call those the six essential low-complexity equal temperaments.
The significance of the septimal comma is successfully recognized by notable notation systems including FJS, HEJI (Helmholtz–Ellis Just Intonation), and Sagittal. It corresponds to the following change of basis, in terms of generator steps.
[math]\displaystyle{ \displaystyle \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \rightarrow \begin{bmatrix} 1 & 1 & 0 & 4 \\ 0 & 1 & 4 & -2 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} }[/math]
Inflected by the commas introduced above, each interval class typically comes in three flavors: a Pythagorean one, a classical one, and a septimal one. The best example for this is the minor third, they are 32/27 (m3), 6/5 (m35), and 7/6 (m37).
Voice leading plays a significant role in traditional harmonies. It is customary to prefer the diatonic semitone to the chromatic semitone for this purpose. Consider 7-limit harmony, the class of diatonic semitones has three notable varieties. Besides 256/243 (m2), there are 16/15 (m25), sharp by 81/80, and 28/27 (m27), flat by 64/63. In 12et, the syntonic comma, the septimal comma and the Pythagorean comma are all tempered out, so all varieties of semitones are conflated as one, which is very adequate for voice leading. The classical diatonic semitone in just intonation, however, is larger. Consequently, the traditional dominant chord using this semitone would be very weak. The Pythagorean variant is not ideal either, since it lacks color and concordance. The septimal version is a much stronger choice.
A basic form of dominant–tonic progression is, therefore, a septimal major triad followed by a classical major triad:
[math]\displaystyle{ \displaystyle 3/2–27/14–9/4 \rightarrow 1–5/4–3/2 }[/math]
where 27/14 resolves to 2/1.
21/20 (m275), the 5/7-kleismic diatonic semitone, is another possible candidate. Compound in color, however, it is not as easy to grasp as 28/27, nor is it as strong, since it is only flat of the Pythagorean version by 5120/5103, the 5/7-kleisma aka the hemififths–amity comma. In contrast, 28/27 creates more cathartic effects for voice leading.
Actually, septimal harmony entail different chord structures from classical ones, and 21/20 has a niche from this perspective. This will be discussed in Chapter VII.
Chapter III. Avicenna's Gift
The harmonics 11 and 13 can be modeled similarly to 5 and 7. 33/32, the undecimal quartertone, lends itself to translate the Pythagorean perfect fourth to 11/8, the octave reduced 11th harmonic. 1053/1024, the tridecimal quartertone, lends itself to translate the Pythagorean minor sixth to 13/8, the octave reduced 13th harmonic.
Again, FJS successfully recognizes these, and extends the mapping to
[math]\displaystyle{ \displaystyle \begin{bmatrix} 1 & 1 & 0 & 4 & 4 & 6 \\ 0 & 1 & 4 & -2 & -1 & -4 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} }[/math]
The four intervals are related through the uniquely most important comma in the 13-limit, 2080/2079, the sinaisma, as
[math]\displaystyle{ \displaystyle 2080/2079 = ((64/63)(1053/1024))/((81/80)(33/32)) }[/math]
The sinaisma fits the difference between eight pairs of 13-limit superparticular commas, not to mention a lot more non-superparticular but useful identities. Its monzo is
[math]\displaystyle{ \displaystyle [ \begin{matrix} 5 & -3 & 1 & -1 & -1 & 1 \end{matrix} \rangle }[/math]
As its orders of 5, 7, 11, and 13 are unity, any no-5, no-7, no-11, or no-13 subgroup temperament can be immediately extended to the full 13-limit by adding this comma to the comma list, and it typically makes sense. The sinaisma is a prime-limit-inclusive fully entangled comma (PIFE comma). As Scott Dakota has noted, these commas are highly portable among numerous systems[5]. Indeed, the sinaismic temperament can be defined by the merge of five comma-size equal temperaments whose tuning profiles are vastly different from each other: 41, 46, 53, 58, and 72. I call those the five essential comma-size equal temperaments.
An equal temperament is a point in the tuning space where it happens to temper out certain additional commas. Appendix D shows a list of efficient 13-limit equal temperaments, gated by TE relative error < 5.5% and cut off at 494. 31 out of the 42 equal temperaments temper out the sinaisma. Although this density drops if the cutoff is set higher, it is expected for any comma.
To temper out the sinaisma requires a fairly accurate representation of harmonic 3, since the corresponding order is three. Meantone or superpyth would not work with it; otherwise it is very portable.
Another potential weakness of the sinaisma is the seesaw effect of error accumulation, observed in 118et, whose tuning profile is given in Figure 2.

118et is famous for being the first equal temperament which clearly gives 5-limit microtempering, with errors well under half a cent. While the harmonics 3 (-0.26 ¢) and 5 (+0.13 ¢) are accurate enough, the 7 (-2.72 ¢) and 11 (-2.17 ¢) are moderately flat. These may not seem much, yet all the errors backfire on the 13 in the same direction, demonstrated below.
[math]\displaystyle{ \displaystyle \begin{align} T \vec m &= 0 \\ T &= T_J + \mathcal{E} \end{align} }[/math]
where T is the tempered tuning map, TJ the just tuning map, Ɛ the error map, and m the monzo of the sinaisma. The error of harmonic 13 is given by
[math]\displaystyle{ \displaystyle \begin{align} \varepsilon_{\pi(13)} &= 3\varepsilon_{\pi(3)} - \varepsilon_{\pi(5)} + \varepsilon_{\pi(7)} + \varepsilon_{\pi(11)} - T_J \vec m \\ &= -3 \times 0.26 - 0.13 - 2.72 - 2.17 - 0.83 ¢ \\ &= -6.63 ¢ \end{align} }[/math]
With optimal octave stretch, it is less cursed, at -4.48 ¢. Although this tuning does nudge it into the range of the closest approximation, the level of stretch has destroyed the microtempering quality of the 5-limit.
The equal temperaments that do not temper out the sinaisma typically miss an accurate harmonic 3 or the aforementioned seesaw effect is too prominent. Examples are 103, 121, and 190.
Another comma that is potentially important is 4096/4095, the schismina. It creates simple connections among 5, 7, and 13. Although not a PIFE comma by definition, it shares virtually all properties with PIFE commas such as the sinaisma. It identifies 1053/1024, the tridecimal quartertone, by 36/35, the septimal one; it also equates 64/63, the septimal comma, with 65/64, the wilsorma. It becomes a dominating comma at a finer tuning resolution.
However, it is still less wise to relate the schismina to the general-purpose 13-limit comma due to its more restrictive nature. Since its monzo is
[math]\displaystyle{ \displaystyle [ \begin{matrix} 12 & -2 & -1 & -1 & 0 & -1 \end{matrix} \rangle }[/math]
the only entry with a positive index is the 2, so tempering it out removes the possibility of all-flat tuning systems. It also has to do with the fact that itself gives us a sharp-tending system as is the case with all commas with a positive index of 2, but it is so small that this sharp tendency is only observable in a very fine level. Actually, if we neglect its size, it removes the possibility of all-sharp tuning systems alike. Furthermore, in any schisminic tunings, the flatter the 3, 5, and 7 are tuned, the sharper the 13 is required to compensate, amplifying the differential error to twice. That is the undesirable quality I call the shearing effect of error accumulation.
Rather than focusing on the case where the schismina is tempered out, its tuning serves as a great indicator of the sharp or flat tendencies of tuning systems, all thanks to its index of 2. A positive schismina signals a flat-tending system, and vice versa.
It is tempting to construct a temperament combining the schismina and the sinaisma due to the identities
[math]\displaystyle{ \displaystyle 2080/2079 = (4096/4095)(4225/4224) }[/math]
An illustration with the context where these intervals occur is given in Figure 3.

This is known as the olympic temperament. Note also tempered out is the olympia, 131072/130977, equating the undecimal quartertone with a stack of two septimal commas. The tempering calls for an accurate tuning of the septimal comma for it to make sense at all, which is not so common. Hence, the portability is remarkably impaired. Plenty of efficient 13-limit equal temperaments do not follow it. Notable examples include 58 and 72.
Chapter IV. Distribution of Superparticular Commas
Superparticular commas are special in that they are more efficient in dominating the tuning. The source is that, up to the same size, they typically have a shorter path in the interval space due to their simplicity. Thus, looking into the distribution of superparticular commas may prove valuable. The phenomenon that the 13-limit optimal tuning often shows a shift from the 11-limit one could be understood as correlated to a distribution shift of superparticular commas. To understand it we need to go through a few superparticular commas first, in particular, superparticular kleismas that form a distribution peak in the 13-limit. They are 352/351 (major minthma), 325/324~385/384 (marveltwin~keenanisma), 364/363~441/440 (minor minthma~werckisma), 540/539~729/728 (swetisma~squbema), and 351/350 (ratwolfsma). Note three of the five come in pairs separated by the sinaisma.
- 352/351 (major minthma)
- Also known as 11/13-kleisma, this comma measures 4.93 ¢ and marks the difference between 11/9 and 39/32, and between 27/22 and 16/13.
- Separated by the sinaisma are also 5120/5103, the 5/7-kleisma aka the hemififths–amity comma, and 847/845, the cuthbert comma.
- 325/324~385/384 (marveltwin~keenanisma)
- The marveltwin measures 5.34 ¢, and is the difference between 16/13 and a stack of two 10/9's or between 13/9 and a stack of two 6/5's.
- The keenanisma measures 4.50 ¢, and is the difference between 33/32 and 36/35.
- 364/363~441/440 (minor minthma~werckisma)
- The minor minthma measures 4.76 ¢, and makes fifth complements of 14/11 and 13/11.
- The werckisma measures 3.93 ¢, and is the difference between 21/20 and 22/21.
- 540/539~729/728 (swetisma~squbema)
- The swetisma measures 3.21 ¢, and is the difference between 15/11 and a stack of two 7/6's or between 33/20 and a stack of two 9/7's.
- The squbema measures 2.38 ¢, and is the difference between 27/26 and 28/27.
- 351/350 (ratwolfsma)
- The ratwolfsma measures 4.94 ¢, and is the difference between 13/10 and 35/27.
All are equipped with respective 13-odd-limit essentially tempered chords, implying their worth of study in far greater detail than this essay can cover.
Since those are five independent commas on top of the sinaisma, it is impossible to temper out all of them (by the rank–nullity theorem). Nonetheless, each of the five essential comma-size equal temperaments does all but one. That which is not tempered out is tuned to one step. 41et does not temper out the ratwolfsma; 46et the swetisma~squbema; 53et the minor minthma~werckisma; 58et the marveltwin~keenanisma; 72et the major minthma. Compare the sizes of those commas and the equal temperament steps. When tempered out, it introduces a kleisma-size error. Otherwise, it introduces a comma-size error. It should be noted that the tuning profiles of those equal temperaments reflect the latter characteristic to a much greater degree.
Notice
[math]\displaystyle{ \displaystyle 41 + 46 + 53 + 58 + 72 = 270 }[/math]
More specifically, it is the vals that add up:
[math]\displaystyle{ \displaystyle V_{41} + V_{46} + V_{53} + V_{58} + V_{72} = V_{270} }[/math]
So 270et is the equal temperament where all those kleismas are tuned to one step, which explains its exceptional strength.
Among the five equal temperaments, 46et is the weakest as the swetisma~squbema pair is too small compared to the other kleismas, yet it is special for the same reason. Observe that
[math]\displaystyle{ \displaystyle 41 + 53 + 58 + 72 = 224 }[/math]
So 224et is the equal temperament where the swetisma~squbema remains tempered out while the other kleismas are tuned to one step. In fact, 224et outperforms all before it and is only bettered by 270et.
224et and 270et can be seen as dual to each other. 224et tempers out the swetisma~squbema; 270et tunes it to one step like the other kleismas. The abigail temperament is the merge of them. It makes the swetisma~squbema a variable while maintaining the other identities. 494et achieves an optimum by tuning the swetisma~squbema to one step and the other kleismas to two steps. This temperament is even more excellent than 270et.
Chapter V. Other Side of the River
Although the FJS is a highly coherent interval space model in the 13-limit, it does not capture the harmonic nature of implicit intervals.
Specifically, quartertones separate interval classes just as semitones do. An implicit interval such as a neutral third is, after all, neither major nor minor, and two neutral thirds make up a perfect fifth. Matthew Yacavone recognized part of this facet and developed the Neutral Functional Just System (NFJS), although it only adopted 2.sqrt (3/2). The sqrt (2).sqrt (3) interval space lends itself better to an enhancement on Pythagorean tuning's role, such that quadratic irrationals are used as anchors for neutrals, interseptimals, quartertones and the tritone.
Quartertones come in different types. Aura analysed quartertones in the 2.3.11 interval space as follows[6]. The first quartertone is the Alpharabian semiaugmented unison, also dubbed the Alpharabian parachromatic quartertone, with the ratio 33/32, measuring 53.3 ¢. Another quartertone is the Alpharabian inframinor second, also dubbed the Alpharabian paradiatonic quartertone, with the ratio 4096/3993, measuring 44.1 ¢. We shall see the whole tone comprises an Alpharabian chromatic semitone and an Alpharabian diatonic semitone. An Alpharabian chromatic semitone comprises two Alpharabian parachromatic quartertones, whereas an Alpharabian diatonic semitone comprises an Alpharabian parachromatic quartertone and an Alpharabian paradiatonic quartertone. Here is an illustration.

The same arithmetics applies to the sqrt (2).sqrt (3) interval space. The Pythagorean parachromatic quartertone has the ratio of sqrt (2187/2048) and the sqrt (2).sqrt (3) subgroup monzo [-11 7⟩, measuring 56.8 ¢. The Pythagorean paradiatonic quartertone has the ratio of sqrt (134217728/129140163) and the sqrt (2).sqrt (3) subgroup monzo [27 -17⟩, measuring 33.4 ¢.
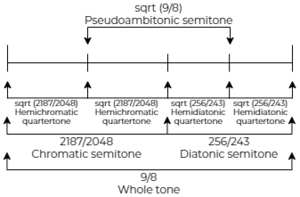
There is a more balanced model for this space, though. Thereby I present three distinct semitones each separated by half the Pythagorean comma.
| Name | Alternative Name | Ratio | S. Monzo | Size (¢) |
|---|---|---|---|---|
| Chromatic semitone | Augmented unison | 2187/2048 | [-22 14⟩ | 113.7 |
| Pseudoambitonal semitone | N/A | sqrt (9/8) | [-3 2⟩ | 102.0 |
| Diatonic semitone | Minor second | 256/243 | [16 -10⟩ | 90.2 |
The pseudoambitonal semitone is the mean of the chromatic and diatonic. It is also the perfect fifth displaced by the semioctave. The term pseudoambitonal is explained later in this chapter.
| Name | Alternative Name | Ratio | S. Monzo | Size (¢) |
|---|---|---|---|---|
| Metachromatic quartertone | N/A | (20 digits) | [-30 19⟩ | 68.6 |
| Hemichromatic quartertone | Semiaugmented unison | sqrt (2187/2048) | [-11 7⟩ | 56.8 |
| Hemidiatonic quartertone | N/A | sqrt (256/243) | [8 -5⟩ | 45.1 |
| Metadiatonic quartertone | Inframinor second | (18 digits) | [27 -17⟩ | 33.4 |
Granted, none of the quartertones is rational. I decide to deviate from Aura's terms only for my own logical coherence: the hemichromatic quartertone is the same as the parachromatic quartertone, and the metadiatonic quartertone is the same as the paradiatonic quartertone.
The hemichromatic quartertone is hemichromatic because it is half the chromatic semitone; same for the hemidiatonic quartertone. We shall see this hemichromatic and hemidiatonic pair is central, in contrast to the hemichromatic and metadiatonic pair shown above. Here is an illustration.
This model allows undecimal intervals to take a new class. Previously, 11/8 is a perfect fourth, and two make up a minor seventh. Now, 11/8 is a semiaugmented fourth, and two make up a major seventh. That undoubtedly captures the harmonic characteristics much better. The 2.3.5.11 subgroup mapping is
[math]\displaystyle{ \displaystyle \begin{bmatrix} 2 & 2 & 0 & 4 \\ 0 & 2 & 8 & 5 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} }[/math]
It follows that 11/8 is the Pythagorean semiaugmented fourth, sqrt (243/128), altered by half the rastma, sqrt (243/242). The half rastma overtakes the role of the undecimal quartertone in the previous model.
Harmonic 11 demonstrates the characteristic of ambitonality. It is ambitonal in the sense that otonal and utonal intervals share the same class. With respect to 5, 5/4 is otonal, and 6/5 is utonal. Like any other classical intervals, they belong to distinct classes. With respect to 11, however, 11/9 is otonal, and 27/22 is utonal. Both are neutral thirds, only separated by the rastma. It even applies to 11/10 and 12/11, separated by the biyatisma, 121/120, which is also commatic since
[math]\displaystyle{ \displaystyle 121/120 = (81/80)/(243/242) }[/math]
Another observation is that all the interval classes of undecimal pairs are implicit, and vice versa, all the implicit interval classes are undecimally ambitonal. Contrarily, sqrt (9/8) is an ambitonal class but takes a position of an explicit interval. That is why it is called the pseudoambitonal semitone, further discussed in Chapter VIII where harmonic 17 will be introduced.
Chapter VI. Semiambitonality
Harmonics 7 and 13 are more complicated cases. Perhaps surprisingly, the septimal comma does not work exactly like the syntonic one. The "septimal minor seventh" is a subminor seventh for a reason. First noted by Aura, this interval does not always manifest itself as a minor seventh[7]:
While many microtonalists think of 7/4 as being purely a type of seventh – and indeed, it most commonly acts as a sort of subminor seventh – I counterargue based on this same interval's relationships with 11/8 in particular that 7/4 is not merely a type of seventh, but rather, a type of a cross between a sixth and a seventh, with such a property explaining why 14/11 is generally considered to be a type of third.
Indeed, 7/4 and its utonal counterpart 12/7 is separated by 49/48, the slendro diesis, only about half the size of 25/24, the classical chroma. See, this size is closer to the rastma than the classical chroma. That reveals how 7/4 can be seen as the Pythagorean hemitwelfth, sqrt (3), altered by half the slendro diesis, sqrt (49/48). In addition to the analysis in Chapter II, we find how septimal intervals have variable harmonic functions.
When 7/4 acts as a hemitwelfth, the harmonic 7 is ambitonal just like 11. Semiambitonality refers to such a condition where the harmonic function is variable, with one being ambitonal and the other not.
As related by the sinaisma, the identity of 13/7 is always a neutral seventh. As such, 13/8 is a subneutral sixth. This means 13/8 can act as a neutral sixth or a major second displaced by a semioctave, and thus tridecimal intervals are also semiambitonal.
The semiambitonality of those harmonics implies two mappings working simultaneously:
[math]\displaystyle{ \displaystyle \begin{bmatrix} 2 & 2 & 0 & 8 & 4 & 8 \\ 0 & 2 & 8 & -4 & 5 & -1 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} }[/math]
and
[math]\displaystyle{ \displaystyle \begin{bmatrix} 2 & 2 & 0 & 5 & 4 & 1 \\ 0 & 2 & 8 & 1 & 5 & 4 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} }[/math]
To summarize:
| Prime Harmonic |
Octave-Reduced Interval Class | Ambitonality |
|---|---|---|
| 5 | Major third | Non-ambitonal |
| 7 | Subminor seventh | Semiambitonal |
| 11 | Semiaugmented fourth | Ambitonal |
| 13 | Subneutral sixth | Semiambitonal |
To incorporate what has been discussed in this chapter, both 7 and 13 are overlaid with the "sub" variation of the first mapping i.e. the NFJS classes. We may well take the second mapping as the basic form, and similarly add "super" variations for the harmonics in question. The first mapping is taken as primary since it is more characteristic and is compatible with traditional heptatonic notation (it is but neutralized diatonic), whereas the second mapping requires the octave to be split. The compatibility allows us to continue using it in chord notation, which marvelously leads us to the next chapter.
Chapter VII. Septimal Chord Construction
The classical major triad is built by 1–3–5, and in compact voicing,
[math]\displaystyle{ \displaystyle 1–5/4–3/2 }[/math]
The classical minor triad is the inverse 1–1/3–1/5, and in compact voicing,
[math]\displaystyle{ \displaystyle 1–6/5–3/2 }[/math]
It is easy to find septimal triads by analogy. For the minor third, 7/6 can be substituted for 6/5. For the major third, 9/7 can be substituted for 5/4. So they are
[math]\displaystyle{ \displaystyle 1–7/6–3/2 \\ 1–9/7–3/2 }[/math]
Unfortunately, they fail to please like their classical counterparts. The classical triads contrast each other through 5/4 and 6/5, with the chroma of 25/24 in between. In septimal, the same gesture should be presented through 7/6 and 8/7. 9/7 is not only a different gesture, but also harms the concordance.
A semiquartal construction is sometimes preferred by those who are aware of that nuance. Typically, they go for
[math]\displaystyle{ \displaystyle 1–7/6–4/3 \\ 1–8/7–4/3 }[/math]
However, those have two issues. First, 4/3, unlike 3/2, lacks the concordance potential in extended voicings. As a result, they only work in the compact voicing. Second, the otonal-7 interval 7/6 is not rooted up to octave equivalence, and thus does not feel resolved.
Strangely enough, I managed to find the right construction. These are still semiquartal constructions, voiced differently:
[math]\displaystyle{ \displaystyle 1–7/4–3 \\ 1–12/7–3 }[/math]
The triads are no longer built by thirds, but by hemitwelfths. That is the compact voicing already. As they contrast each other through 7/4 and 12/7, with the chroma of 49/48 in between, it is revealed how they form exactly the same gesture as classical triads.
It has never been specified how chords should be notated in FJS and its derivatives. Here is my proposal. The classical major triad, when built on C, is CM5. The M must not be omitted for obvious reasons. The classical minor triad, when built on A, is Am5. The septimal triads can be notated as C5m77 and A5M67, respectively. I provide shortcuts CH7 and Ah7 to highlight their close relations. The H and h stand for hemitwelfth. By design, they are preprocessed characters that have nothing to do with semantics, and definitely do not "escape" what follows. Users are supposed to still treat the superscript and subscript 7 as alterations by the septimal comma.
Yet another problem in septimal harmony is that they miss leading tones. Leading tones are minor seconds or major sevenths to the tonal root, corresponding to 5 generator steps[8]. As the major third is 4 generator steps, classical harmony features a leading tone in the dominant position for major, and subdominant position for minor, even though it is weak. Septimal harmony misses it since the maximal number of generator steps in the septimal triads is only 3.
As a result, the septimal cadence calls for tetrads, and works very differently.
In major, it is built on the subdominant. Itself is
[math]\displaystyle{ \displaystyle 1–7/4–7/3–3 }[/math]
With respect to the tonic, it is
[math]\displaystyle{ \displaystyle 4/3–7/3–28/9–4 \rightarrow 1–7/4–3 }[/math]
with the voice leading featuring 28/27 at 28/9 → 3. In C major, it is FmH7 → CH7. Although pedantically there is not a leading tone as it resolves to the fifth instead of the tonal root, the tension is real and the technique is attested in traditional harmony in the form of harmonic major and harmonic minor.
In minor, it is built on the dominant. Itself is
[math]\displaystyle{ \displaystyle 1–9/7–12/7–3 }[/math]
With respect to the tonic, it is
[math]\displaystyle{ \displaystyle 3/4–27/28–9/7–9/4 \rightarrow 1–12/7–3 }[/math]
with the same voice leading at 27/28 → 1. In A minor, it is EMh7 → Ah7. Again there is not a leading tone in the context of harmonic dualism.
Similar to traditional harmony, the modes of harmonic major or minor are available.
Harmonic major borrows the minor chord for major:
[math]\displaystyle{ \displaystyle 3/4–27/28–9/7–9/4 \rightarrow 1–7/4–3 }[/math]
In C major, it is GMh7 → CH7. Now there is truly a leading tone, as it resolves to the tonal root.
Harmonic minor borrows the major chord for minor:
[math]\displaystyle{ \displaystyle 4/3–7/3–28/9–4 \rightarrow 1–12/7–3 }[/math]
In A minor, it is DmH7 → Ah7. Like harmonic major, a leading tone is present.
Another possible dominant–tonic resolution is a septimal to classical one. It does not call for tetrads. That is where the 5/7-kleismic minor second shines.
[math]\displaystyle{ \displaystyle 3/4–21/16–9/4 \rightarrow 1–5/4–3/2 }[/math]
with the voice leading at 21/16 → 5/4 characterized by 21/20. In C major, it is GH7 → CM5.
The negative harmony version is
[math]\displaystyle{ \displaystyle 2/3–8/7–2 \rightarrow 1–6/5–3/2 }[/math]
with the same voice leading at 8/7 → 6/5. In A minor, it is Dh7 → Am5.
As one might expect, the reverse, a classical to septimal one, works as well.
[math]\displaystyle{ \displaystyle 4/3–5/3–2 \rightarrow 1–7/4–3 }[/math]
with the same voice leading at 5/3 → 7/4. In C major, it is FM5 → CH7.
The negative harmony version is
[math]\displaystyle{ \displaystyle 3/2–9/5–9/4 \rightarrow 1–12/7–3 }[/math]
with the same voice leading at 9/5 → 12/7. In A minor, it is Em5 → Ah7.
The four septimal cadences and the four septimal–classical cadences above, in addition to the four classical cadences, serve as the basis for more advanced chord progressions. Undecimal and tridecimal triads can be constructed in a similar way, but they are more complex. Speculation suggests that 11 works like 5, and 13 works like 7. Even better, they tend to work with extended chords. Obviously, I have to save them for another episode.
Chapter VIII. Transtridecimal Realms
Prime harmonics beyond 13 are difficult. To be clear, 13-limit adds little complexity to 11-limit thanks to the excellence of the sinaisma. A similar comma in the 17-limit and beyond is not found. Nonetheless, study has been somewhat fruitful. Here is my result.
| Prime Harmonic |
Octave-Reduced Interval Class | Ambitonality |
|---|---|---|
| 17 | Pseudoambitonal semitone | Pseudoambitonal |
| 19 | Pseudoambitonal sesquitone | Pseudoambitonal |
| 23 | Subsemidiminished fifth | Semiambitonal |
| 29 | Subneutral seventh | Semiambitonal |
| 31 | Semidiminished octave | Ambitonal |
The pseudoambitonal quality sees an application in the 17-limit. 17/16 is both a minor second and an augmented unison. It is a pseudoambitonal semitone. There is no functional distinction between otonal-17 and utonal-17. 289/288, the semitonisma, works like the rastma. When septendecimal intervals are separated by this comma, the larger one is dubbed large and the smaller one is dubbed small.
The class of 19 is inferred by treating 19/17 as a major second because both 9/8 and 10/9 are major seconds. Consequently, 19 is both a minor third and an augmented second. As such, both 19/18 and 20/19 are pseudoambitonal semitones. So is 81/76, the remaining part of the tone subtracted by 19/18.
29/23 is a major third. However, both 23 and 29 are entangled with 13 by treating 26/23 and 29/26 as major seconds, so both are semiambitonal. 23 is subsemidiminished, and 29 is subneutral. 31 works exactly the same as 11. The tricesimoprimal counterpart of the rastma is 972/961.
Looking deep into 17-limit reveals some interesting structural implications and tempering options. After all, one additional factor for a solved system should be manageable.
The 17-limit has two notable quartertones, 34/33 and 35/34, in addition to the septimal and undecimal ones. If one starts counting quartertones with 33/32 and stops at 36/35 (since a whole tone can be split into (33/32)(34/33)(35/34)(36/35)), then the two 17-limit quartertones fill right in the gap. 34/33 differs from 33/32 by 1089/1088, the twosquare comma. 35/34 differs from 36/35 by 1225/1224, the noellisma. The two 17-limit quartertones are apart by 1156/1155, the quadrantonisma.
9801/9800, the kalisma, is famous for being the smallest 11-limit superparticular comma, and for having the octave split into two equal parts, each representing 99/70~140/99 in kalismic tempering. Together with the sinaisma we obtain {1716/1715, 2080/2079}, a wonderful 13-limit temperament with a semioctave. Moreover, it is the difference between the twosquare comma and the noellisma:
[math]\displaystyle{ \displaystyle 9801/9800 = (1089/1088)/(1225/1224) }[/math]
Kalismic tempering therefore not only offers a semioctave, but also symmetry in the four quartertones, in that 33/32 to 34/33 is equidistant to 35/34 to 36/35.
With the two 17-limit quartertones there are also two 17-limit sixth-tones, 51/50 and 52/51. If one starts counting from 49/48 and stops at 54/53 (since a whole tone can be split into (49/48)(50/49)(51/50)(52/51)(53/52)(54/53)), then the two 17-limit sixth-tones are, again, located at the center. They are apart by 2601/2600, the sextantonisma.
Here is the most interesting part. The difference between the quadrantonisma and the sextantonisma is not anything else but the sinaisma:
[math]\displaystyle{ \displaystyle 2080/2079 = (1156/1155)/(2601/2600) }[/math]
So we see how 17 can be related to the 13-limit via the system {1156/1155, 1716/1715, 2080/2079}. The full distinction of the four quartertones requires that the keenanisma be split into three parts, which might be too complex a system for any human being to grasp, so this system is a good compromise. It equates 34/33 with 35/34, and 51/50 with 52/51, offering three distinct equidistant quartertones: 33/32, 34/33~35/34, 36/35. Another system, {715/714, 1089/1088, 1225/1224}, does the opposite. It equates 34/33 with 33/32 and 35/34 with 36/35, leaving two quartertones: 33/32~34/33, 35/34~36/35. The former is optimized by a flat tuning of 17 and the latter by a sharp tuning.
Finally, I would like to briefly cover the 19-limit. The tuning of 19/17, being the mediant of 10/9 and 9/8, is presumably one of the focuses. 1445/1444, the aureusma, identifies the distance difference of 19/17 to 9/8 and to 10/9. To capture 19/17, the simplest full 19-limit tempered system must contain hemicomma steps, that is, it splits the syntonic comma into two equal steps, tempering out the aureusma. That explains how none of the five essential comma-size equal temperaments extends smoothly to the full 19-limit – they all miss 19/17, such that they hit one harmonic and miss the other. Even though hemicomma-size systems tend to hit 19/17, there is a fair chance they miss both harmonics. That is why full 19-limit equal temperaments are so rare.
Appendix A. Number Symbolism
For what it is worth, this is how I sometimes relate each prime harmonic.
- 2: self
- The 2nd harmonic is the tonic itself, so this number symbolizes the self and the coming into being. Its color is transparent.
- 3: aether
- The Pythagorean intervals are like channels where the root can traverse around, just like aether, the medium where light travels. Its color is gray.
- 5: earth
- 5 symbolizes the solid, the warm, and the stable. Its color is yellow.
- 7: air
- 7 symbolizes the pure, the fresh, and the mobile. Its color is blue.
- 11: water
- 11 symbolizes the graceful and the devoted. Its color is green.
- 13: fire
- 13 symbolizes the fierce conflict and the refusal to compromise. Its color is magenta.
Appendix B. Concepts
- Consonance and concordance
Consonance and concordance are distinct concepts. Consonance is contextual i.e. it is correlated with both the temporal and frequential relative position of the chord. Concordance only has to do with the chord structure itself[9].
Chords in common practice could be consonant or dissonant, but most if not all of them were concordant. The dominant seventh chord, for example, is an essentially tempered chord in septimal meantone, where every dyad is a member of the 9-odd-limit tonality diamond.
As another example, 12et contains virtually no discordance, either. Every interval has simple ratio interpretations, and it was this basis that empowered Schoenberg to develop the 12-tone serialism.
- Harmonic, melodic, and commatic functions
By a harmonic function is meant an interval, when played simultaneously or successively, induces harmony, that is, consonance, dissonance or similar musical feelings arising from temporal–frequential interactions of the signals.
By a melodic function is meant an interval, when played successively, induces musical feelings reminiscent of experience of spatial patterns.
By a commatic function is meant an interval that lacks sense if played either simultaneously or successively, but fits the color difference between other intervals.
The smallest interval that demonstrates harmonic functions measures about a third tone. Beyond that, the harmonic functionality falls quickly. Quartertones virtually miss harmonic functions, but they are rich in melodic and commatic functions. The smallest interval that demonstrates melodic functions measures about a diesis. Smaller than the diesis is a comma, which misses harmonic and melodic functions, and only demonstrates commatic functions.
Appendix C. Naming of Several Commas
A number of ratios have made meaningful appearances in this analysis, and of course, some of them are necessary for describing the canou temperament, {1216/1215, 1225/1224, 1445/1444}.
289/288 is the semitonisma, which is a contraction of septendecimal semitones comma into a single word consisting of Latin semi ("half") and tonus ("tone").
1156/1155 is the quadrantonisma, which is a contraction of septendecimal quartertones comma into a single word consisting of Latin quadrans ("fourth") and tonus ("tone").
2601/2600 is the sextantonisma, which is a contraction of septendecimal sixth-tones comma into a single word consisting of Latin sextans ("sixth") and tonus ("tone").
1225/1224 is the noellisma, which derives from the name Noel, because the numerator or the denominator, when written in decimal system, is reminiscent of the date of Christmas.
1445/1444 is the aureusma, which derives from Latin aureus ("golden"), for its possible association with golden meantone.
Appendix D. Table of 13-Limit Equal Temperaments
TE relative error < 5.5% and cutoff at 494. Sorted by step number of the syntonic comma.
| ET | Step Size (¢) |
Characteristic Ratio |
Rating (%) |
Comma Basis |
|---|---|---|---|---|
| 31 | 38.7 | 45/44 | 5.35 | 66/65, 81/80, 99/98, 105/104, 121/120 |
| 41 | 29.3 | 64/63 | 5.29 | 100/99, 105/104, 144/143, 196/195, 243/242 |
| 46 | 26.1 | 66/65 | 5.42 | 91/90, 121/120, 169/168, 176/175, 245/243 |
| 53 | 22.6 | 78/77 | 5.22 | 99/98, 121/120, 169/168, 176/175, 275/273 |
| 58 | 20.7 | 81/80 | 4.56 | 126/125, 144/143, 176/175, 196/195, 364/363 |
| 72 | 16.7 | 100/99 | 3.82 | 169/168, 225/224, 243/242, 325/324, 385/384 |
| 103 | 11.7 | 144/143 | 4.90 | 225/224, 243/242, 351/350, 385/384, 847/845 |
| 87 | 13.8 | 121/120 | 4.53 | 196/195, 245/243, 352/351, 364/363, 625/624 |
| 94 | 12.8 | 144/143 | 5.48 | 225/224, 275/273, 325/324, 385/384, 1331/1323 |
| 111 | 10.8 | 169/168 | 5.21 | 176/175, 351/350, 540/539, 676/675, 1331/1323 |
| 130 | 9.23 | 196/195 | 3.98 | 243/242, 351/350, 364/363, 441/440, 3136/3125 |
| 121 | 9.91 | 176/175 | 5.14 | 325/324, 352/351, 364/363, 540/539, 625/624 |
| 140 | 8.57 | 196/195 | 4.68 | 325/324, 352/351, 385/384, 625/624, 1331/1323 |
| 152f | 7.89 | 225/224 | 4.73 | 352/351, 540/539, 625/624, 729/728, 1575/1573 |
| 159 | 7.55 | 225/224 | 5.11 | 325/324, 364/363, 385/384, 625/624, 10976/10935 |
| 183 | 6.56 | 243/242 | 4.70 | 351/350, 540/539, 676/675, 1375/1372, 4096/4095 |
| 190 | 6.32 | 243/242 | 4.63 | 385/384, 441/440, 625/624, 729/728, 847/845 |
| 198 | 6.06 | 325/324 | 4.50 | 352/351, 676/675, 847/845, 1716/1715, 3025/3024 |
| 212 | 5.66 | 351/350 | 5.23 | 325/324, 385/384, 625/624, 1375/1372, 10648/10647 |
| 217 | 5.53 | 325/324 | 5.08 | 364/363, 441/440, 676/675, 3136/3125, 4375/4374 |
| 224 | 5.36 | 325/324 | 3.37 | 540/539, 625/624, 729/728, 1375/1372, 2200/2197 |
| 270 | 4.44 | 385/384 | 2.48 | 676/675, 1001/1000, 1716/1715, 3025/3024, 4096/4095 |
| 282 | 4.25 | 441/440 | 5.07 | 540/539, 729/728, 1575/1573, 2200/2197, 3584/3575 |
| 296 | 4.05 | 441/440 | 5.44 | 540/539, 625/624, 729/728, 1375/1372, 15379/15360 |
| 301 | 3.99 | 441/440 | 4.60 | 729/728, 847/845, 1001/1000, 1716/1715, 3025/3024 |
| 320 | 3.75 | 540/539 | 5.31 | 441/440, 729/728, 1001/1000, 4225/4224, 6656/6655 |
| 311 | 3.86 | 441/440 | 3.81 | 625/624, 1575/1573, 2080/2079, 2200/2197, 2401/2400 |
| 328 | 3.66 | 441/440 | 5.15 | 676/675, 1001/1000, 1716/1715, 3136/3125, 10648/10647 |
| 342f | 3.51 | 540/539 | 4.61 | 676/675, 1001/1000, 1716/1715, 3025/3024, 19773/19712 |
| 354 | 3.39 | 441/440 | 4.93 | 540/539, 729/728, 1575/1573, 4096/4095, 31250/31213 |
| 373 | 3.22 | 540/539 | 4.12 | 729/728, 1001/1000, 1716/1715, 3025/3024, 4225/4224 |
| 364 | 3.30 | 540/539 | 4.92 | 625/624, 1375/1372, 2080/2079, 2200/2197, 14641/14625 |
| 369f | 3.25 | 540/539 | 5.24 | 1575/1573, 2080/2079, 2200/2197, 2401/2400, 3584/3575 |
| 383 | 3.13 | 540/539 | 4.87 | 625/624, 1575/1573, 2080/2079, 2401/2400, 10985/10976 |
| 400 | 3.00 | 540/539 | 4.69 | 676/675, 1001/1000, 1716/1715, 4096/4095, 39366/39325 |
| 414 | 2.90 | 540/539 | 4.94 | 625/624, 729/728, 1575/1573, 2200/2197, 2401/2400 |
| 431 | 2.78 | 676/675 | 5.38 | 729/728, 1001/1000, 1716/1715, 4096/4095, 6656/6655 |
| 422 | 2.84 | 625/624 | 4.02 | 1716/1715, 2080/2079, 2200/2197, 3025/3024, 5632/5625 |
| 441 | 2.72 | 625/624 | 4.12 | 1575/1573, 2080/2079, 2401/2400, 4096/4095, 4375/4374 |
| 460 | 2.61 | 676/675 | 4.36 | 1001/1000, 3025/3024, 4225/4224, 4375/4374, 26411/26364 |
| 472 | 2.54 | 625/624 | 5.37 | 729/728, 1575/1573, 2200/2197, 2401/2400, 4096/4095 |
| 494 | 2.43 | 729/728 | 2.37 | 1716/1715, 2080/2079, 3025/3024, 4096/4095, 31250/31213 |
Notes
- ↑ The FJS Crash Course. Misotanni. The Functional Just System.
- ↑ Diatonic, Chromatic, Enharmonic, Subchromatic. Mike Battaglia. Xenharmonic Wiki.
- ↑ These are commonly accepted names. They are not exactly logical, but it will only confuse if I introduce new terms at this point. I only modified classic to classical because I suspect classic is a misnomer.
- ↑ The 17-tone Puzzle – And the Neo-medieval Key That Unlocks It. George Secor. Anaphoria.
- ↑ Casually noted by Scott Dakota in online chats, although the sinaisma was not one of the two explicitly recognized commas.
- ↑ Aura's Ideas on Tonality. Aura. Xenharmonic Wiki.
- ↑ Aura's Ideas on Functional Harmony. Aura. Xenharmonic Wiki.
- ↑ Tonal root is my ad hoc neologism referring to the root of the tonic chord in the context of harmonic dualism. It is the tonic for major keys and the dominant for minor keys.
- ↑ Harmonic entropy. Mike Battaglia. Xenharmonic Wiki.
Release Notes
© 2022–2024 Flora Canou
Version Stable 7 Beta 0
This work is licensed under the Creative Commons Attribution-ShareAlike 4.0 International License.