6edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older editNewer edit →
VisualWikitext
ArrowHead294 (talk | contribs)
14,512 edits
mNo edit summary
Line 7: Line 7:
{{Infobox ET}}
{{Infobox ET}}
{{Wikipedia|Whole tone scale}}
{{Wikipedia|Whole tone scale}}
{{EDO intro|6}}  
{{ED intro}} It is also known as the '''whole tone scale'''.  
 
6edo is also known as the '''whole tone scale'''.  


== Theory ==
== Theory ==
As a subset of [[12edo]], 6edo can be notated on a five-line staff with standard notation. It is the first [[edo]] that is not a [[zeta peak edo|zeta peak]], has lower [[Consistency limits of small EDOs|consistency]] than the one that precedes it, and the highest edo that has no single period mode of symmetry scales other than using the single step as a generator. This means it is relatively poor for its size at creating traditional tonal music, with 5edo and 7edo both having much better representations of the third harmonic, but has still seen more use than most edos other than 12, since it can be played on any 12-tone instrument.
As a subset of [[12edo]], 6edo can be notated on a five-line staff with standard notation. It is the first [[edo]] that is not a [[zeta peak edo|zeta peak]], has lower [[Consistency limits of small EDOs|consistency]] than the one that precedes it, and the highest edo that has no single period mode of symmetry scales other than using the single step as a generator. This means it is relatively poor for its size at creating traditional tonal music, with 5edo and 7edo both having much better representations of the third harmonic, but has still seen more use than most edos other than 12, since it can be played on any 12-tone instrument.


Line 26: Line 23:
== Intervals ==
== Intervals ==
{| class="wikitable center-all"
{| class="wikitable center-all"
|+ Intervals of 6edo
|+ style="font-size: 105%;" | Intervals of 6edo
|-
! rowspan="2" | [[Degree]]
! rowspan="2" | [[Degree]]
! rowspan="2" | [[Cent]]s
! rowspan="2" | [[Cent]]s
! rowspan="2" | [[Interval region]]
! rowspan="2" | [[Interval region]]
! colspan="4" | Approximated [[JI]] intervals* ([[error]] in [[¢]])
! colspan="4" | Approximated [[JI]] intervals<ref group="note">{{sg|limit=subset of 12edo, itself treated as a 2.3.5.7.17.19 subgroup}} For example, for 6edo as a 2.5.7.9 subgroup temperament, ignore the "Other" column).</ref>
! rowspan="2" | Audio
! rowspan="2" | Audio
|-
|-
Line 50: Line 48:
| 200
| 200
| Major second
| Major second
| [[9/8]] (-3.910)
| [[9/8]] (−3.910)
| [[10/9]] (+17.596)
| [[10/9]] (+17.596)
| [[28/25]] (+3.802)<br>[[8/7]] (-31.174)
| [[28/25]] (+3.802)<br />[[8/7]] (−31.174)
| [[19/17]] (+7.442)<br>[[55/49]] (+0.020)<br>[[64/57]] (-0.532)<br>[[17/15]] (-16.687)
| [[19/17]] (+7.442)<br />[[55/49]] (+0.020)<br />[[64/57]] (−0.532)<br />[[17/15]] (−16.687)
| [[File:piano_1_6edo.mp3]]
| [[File:piano_1_6edo.mp3]]
|-
|-
Line 59: Line 57:
| 400
| 400
| Major third
| Major third
| [[81/64]] (-7.820)
| [[81/64]] (−7.820)
| [[5/4]] (+13.686)
| [[5/4]] (+13.686)
| [[63/50]] (-0.108)<br>[[9/7]] (-35.084)
| [[63/50]] (−0.108)<br />[[9/7]] (−35.084)
| [[34/27]] (+0.910)
| [[34/27]] (+0.910)
| [[File:piano_1_3edo.mp3]]
| [[File:piano_1_3edo.mp3]]
Line 70: Line 68:
|  
|  
|  
|  
| [[7/5]] (+17.488)<br>[[10/7]] (-17.488)
| [[7/5]] (+17.488)<br />[[10/7]] (−17.488)
| [[24/17]] (+3.000)<br>[[99/70]] (-0.088)<br>[[17/12]] (-3.000)
| [[24/17]] (+3.000)<br />[[99/70]] (−0.088)<br />[[17/12]] (−3.000)
| [[File:piano_1_2edo.mp3]]
| [[File:piano_1_2edo.mp3]]
|-
|-
Line 78: Line 76:
| Minor sixth
| Minor sixth
| [[128/81]] (+7.820)
| [[128/81]] (+7.820)
| [[8/5]] (-13.686)
| [[8/5]] (−13.686)
| [[14/9]] (+35.084)<br>[[100/63]] (+0.108)
| [[14/9]] (+35.084)<br />[[100/63]] (+0.108)
| [[27/17]] (-0.910)
| [[27/17]] (−0.910)
| [[File:piano_2_3edo.mp3]]
| [[File:piano_2_3edo.mp3]]
|-
|-
Line 87: Line 85:
| Minor seventh
| Minor seventh
| [[16/9]] (+3.910)
| [[16/9]] (+3.910)
| [[9/5]] (-17.596)
| [[9/5]] (−17.596)
| [[7/4]] (+31.174)<br>[[25/14]] (-3.802)
| [[7/4]] (+31.174)<br />[[25/14]] (−3.802)
| [[30/17]] (+16.687)<br>[[57/32]] (+0.532)<br>[[98/55]] (-0.020)<br>[[34/19]] (-7.442)
| [[30/17]] (+16.687)<br />[[57/32]] (+0.532)<br />[[98/55]] (−0.020)<br />[[34/19]] (−7.442)
| [[File:piano_5_6edo.mp3]]
| [[File:piano_5_6edo.mp3]]
|-
|-
Line 101: Line 99:
| [[File:piano_1_1edo.mp3]]
| [[File:piano_1_1edo.mp3]]
|}
|}
<nowiki>*</nowiki> based on treating 6edo as a subset of 12edo, itself treated as a 2.3.5.7.17.19 subgroup temperament; other approaches are possible (e.g. for 6edo as a 2.5.7.9 subgroup temperament, ignore the "Other" column).


== Notation ==
== Notation ==
{| class="wikitable center-all"
{| class="wikitable center-all"
|+ Notation of 6edo
|+ style="font-size: 105%;" | Notation of 6edo
|-
! rowspan="2" | [[Degree]]
! rowspan="2" | [[Degree]]
! rowspan="2" | [[Cent]]s
! rowspan="2" | [[Cent]]s
Line 121: Line 118:
| 1
| 1
| 200
| 200
| '''Major second (M2)'''<br>Diminished third (d3)
| '''Major second (M2)'''<br />Diminished third (d3)
| '''E'''<br>Fb
| '''E'''<br />Fb
|-
|-
| 2
| 2
| 400
| 400
| Major third (M3)<br>Diminished fourth (d4)
| Major third (M3)<br />Diminished fourth (d4)
| F#<br>Gb
| F#<br />Gb
|-
|-
| 3
| 3
| 600
| 600
| Augmented fourth (A4)<br>Diminished fifth (d5)
| Augmented fourth (A4)<br />Diminished fifth (d5)
| G#<br>Ab
| G#<br />Ab
|-
|-
| 4
| 4
| 800
| 800
| Augmented fifth (A5)<br>Minor sixth (m6)
| Augmented fifth (A5)<br />Minor sixth (m6)
| A#<br>Bb
| A#<br />Bb
|-
|-
| 5
| 5
| 1000
| 1000
| Augmented sixth (A6)<br>'''Minor seventh (m7)'''
| Augmented sixth (A6)<br />'''Minor seventh (m7)'''
| B#<br>'''C'''
| B#<br />'''C'''
|-
|-
| 6
| 6
Line 154: Line 151:
* mixed [[sagittal notation]] is identical to standard notation, but pure sagittal notation exchanges sharps (#) and flats (b) for sagittal sharp ([[File:Sagittal sharp.png]]) and sagittal flat ([[File:Sagittal flat.png]]) respectively.
* mixed [[sagittal notation]] is identical to standard notation, but pure sagittal notation exchanges sharps (#) and flats (b) for sagittal sharp ([[File:Sagittal sharp.png]]) and sagittal flat ([[File:Sagittal flat.png]]) respectively.


===Sagittal notation===
=== Sagittal notation ===
This notation is a subset of the notations for EDOs [[12edo#Sagittal notation|12]], [[18edo#Sagittal notation|18]], [[24edo#Sagittal notation|24]], [[36edo#Sagittal notation|36]], [[48edo#Sagittal notation|48]], [[60edo#Sagittal notation|60]], [[72edo#Sagittal notation|72]], and [[84edo#Sagittal notation|84]].
This notation is a subset of the notations for EDOs [[12edo#Sagittal notation|12]], [[18edo#Sagittal notation|18]], [[24edo#Sagittal notation|24]], [[36edo#Sagittal notation|36]], [[48edo#Sagittal notation|48]], [[60edo#Sagittal notation|60]], [[72edo#Sagittal notation|72]], and [[84edo#Sagittal notation|84]].
====Evo flavor====


==== Evo flavor ====
<imagemap>
<imagemap>
File:6-EDO_Evo_Sagittal.svg
File:6-EDO_Evo_Sagittal.svg
Line 169: Line 166:
Because it includes no Sagittal symbols, this Evo Sagittal notation is also a conventional notation.
Because it includes no Sagittal symbols, this Evo Sagittal notation is also a conventional notation.


====Revo flavor====
==== Revo flavor ====
 
<imagemap>
<imagemap>
File:6-EDO_Revo_Sagittal.svg
File:6-EDO_Revo_Sagittal.svg
Line 182: Line 178:
== Solfege ==
== Solfege ==
{| class="wikitable center-all"
{| class="wikitable center-all"
|+ Solfege of 6edo
|+ style="font-size: 105%;" | Solfege of 6edo
|-
! [[Degree]]
! [[Degree]]
! [[Cents]]
! [[Cents]]
! 12edo subset<br>standard [[solfege]]<br>(movable do)
! 12edo subset<br />standard [[solfege]]<br />(movable do)
! 12edo subset<br>[[uniform solfege]]<br>(2-3 vowels)
! 12edo subset<br />[[uniform solfege]]<br />(2–3 vowels)
|-
|-
| 0
| 0
Line 201: Line 198:
| 400
| 400
| Mi
| Mi
| Ma (M3)<br>Fo (d4)
| Ma (M3)<br />Fo (d4)
|-
|-
| 3
| 3
| 600
| 600
| Fi (A4)<br>Se (d5)
| Fi (A4)<br />Se (d5)
| Pa (A4)<br>Sha (d5)
| Pa (A4)<br />Sha (d5)
|-
|-
| 4
| 4
| 800
| 800
| Si (A5)<br>Le (m6)
| Si (A5)<br />Le (m6)
| Su (A5)<br>Fla (m6)
| Su (A5)<br />Fla (m6)
|-
|-
| 5
| 5
| 1000
| 1000
| Li (A6)<br>Te (m7)
| Li (A6)<br />Te (m7)
| Lu (A6)<br>Tha (m7)
| Lu (A6)<br />Tha (m7)
|-
|-
| 6
| 6
Line 233: Line 230:
{| class="commatable wikitable center-1 center-2 right-4 center-5"
{| class="commatable wikitable center-1 center-2 right-4 center-5"
|-
|-
! [[Harmonic limit|Prime<br>limit]]
! [[Harmonic limit|Prime<br />limit]]
! [[Ratio]]<ref group="note">Ratios longer than 10 digits are presented by placeholders with informative hints</ref>
! [[Ratio]]<ref group="note">{{rd}}</ref>
! [[Monzo]]
! [[Monzo]]
! [[Cent]]s
! [[Cent]]s
Line 345: Line 342:
| Tridecimal neutral second
| Tridecimal neutral second
|}
|}
<references group="note"/>


== Music ==
== Music ==
Line 370: Line 366:
; [[Chris Vaisvil]]
; [[Chris Vaisvil]]
* ''The Good Boundless'' (2011) – [https://www.chrisvaisvil.com/the-good-boundless/ blog] | [https://web.archive.org/web/20230530111053/http://micro.soonlabel.com/6edo/the-good-boundless-03.mp3 play]
* ''The Good Boundless'' (2011) – [https://www.chrisvaisvil.com/the-good-boundless/ blog] | [https://web.archive.org/web/20230530111053/http://micro.soonlabel.com/6edo/the-good-boundless-03.mp3 play]
== Notes ==
<references group="note" />


[[Category:6-tone scales]]
[[Category:6-tone scales]]
[[Category:Listen]]
[[Category:Listen]]
[[Category:Macrotonal]]
[[Category:Macrotonal]]

Revision as of 15:58, 20 February 2025

← 5edo 6edo 7edo →
Prime factorization 2 × 3
Step size 200 ¢ 
Fifth 4\6 (800 ¢) (→ 2\3)
Semitones (A1:m2) 4:-2 (800 ¢ : -400 ¢)
Dual sharp fifth 4\6 (800 ¢) (→ 2\3)
Dual flat fifth 3\6 (600 ¢) (→ 1\2)
Dual major 2nd 1\6 (200 ¢)
(convergent)
Consistency limit 7
Distinct consistency limit 3
Special properties
English Wikipedia has an article on:

6 equal divisions of the octave (abbreviated 6edo or 6ed2), also called 6-tone equal temperament (6tet) or 6 equal temperament (6et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 6 equal parts of exactly 200 ¢ each. Each step represents a frequency ratio of 21/6, or the 6th root of 2. It is also known as the whole tone scale.

Theory

As a subset of 12edo, 6edo can be notated on a five-line staff with standard notation. It is the first edo that is not a zeta peak, has lower consistency than the one that precedes it, and the highest edo that has no single period mode of symmetry scales other than using the single step as a generator. This means it is relatively poor for its size at creating traditional tonal music, with 5edo and 7edo both having much better representations of the third harmonic, but has still seen more use than most edos other than 12, since it can be played on any 12-tone instrument.

While 6edo does not well approximate the 3rd harmonic, it does contain a good approximation of the 9th harmonic. Therefore, 6edo can be treated as a 2.9.5.7-subgroup temperament.

Odd harmonics

Approximation of odd harmonics in 6edo
Harmonic 3 5 7 9 11 13 15 17 19 21 23
Error Absolute (¢) +98.0 +13.7 +31.2 -3.9 +48.7 -40.5 -88.3 +95.0 -97.5 -70.8 -28.3
Relative (%) +49.0 +6.8 +15.6 -2.0 +24.3 -20.3 -44.1 +47.5 -48.8 -35.4 -14.1
Steps
(reduced) 		10
(4) 		14
(2) 		17
(5) 		19
(1) 		21
(3) 		22
(4) 		23
(5) 		25
(1) 		25
(1) 		26
(2) 		27
(3)

Subsets and supersets

Intervals

Intervals of 6edo
Degree Cents Interval region Approximated JI intervals[note 1] Audio
3-limit 5-limit 7-limit Other
0 0 Unison (prime) 1/1 (just)
1 200 Major second 9/8 (−3.910) 10/9 (+17.596) 28/25 (+3.802)
8/7 (−31.174) 		19/17 (+7.442)
55/49 (+0.020)
64/57 (−0.532)
17/15 (−16.687)
2 400 Major third 81/64 (−7.820) 5/4 (+13.686) 63/50 (−0.108)
9/7 (−35.084) 		34/27 (+0.910)
3 600 Tritone 7/5 (+17.488)
10/7 (−17.488) 		24/17 (+3.000)
99/70 (−0.088)
17/12 (−3.000)
4 800 Minor sixth 128/81 (+7.820) 8/5 (−13.686) 14/9 (+35.084)
100/63 (+0.108) 		27/17 (−0.910)
5 1000 Minor seventh 16/9 (+3.910) 9/5 (−17.596) 7/4 (+31.174)
25/14 (−3.802) 		30/17 (+16.687)
57/32 (+0.532)
98/55 (−0.020)
34/19 (−7.442)
6 1200 Octave 2/1 (just)

Notation

Notation of 6edo
Degree Cents 12edo subset notation
Diatonic interval names Note names (on D)
0 0 Perfect unison (P1) D
1 200 Major second (M2)
Diminished third (d3) 		E
Fb
2 400 Major third (M3)
Diminished fourth (d4) 		F#
Gb
3 600 Augmented fourth (A4)
Diminished fifth (d5) 		G#
Ab
4 800 Augmented fifth (A5)
Minor sixth (m6) 		A#
Bb
5 1000 Augmented sixth (A6)
Minor seventh (m7) 		B#
C
6 1200 Perfect octave (P8) D

In 6edo:

  • ups and downs notation is identical to standard notation;
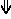  • mixed sagittal notation is identical to standard notation, but pure sagittal notation exchanges sharps (#) and flats (b) for sagittal sharp () and sagittal flat () respectively.

Sagittal notation

This notation is a subset of the notations for EDOs 12, 18, 24, 36, 48, 60, 72, and 84.

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation12-EDO notation

Because it includes no Sagittal symbols, this Evo Sagittal notation is also a conventional notation.

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation12-EDO notation

Solfege

Solfege of 6edo
Degree Cents 12edo subset
standard solfege
(movable do) 		12edo subset
uniform solfege
(2–3 vowels)
0 0 Do Da
1 200 Re Ra
2 400 Mi Ma (M3)
Fo (d4)
3 600 Fi (A4)
Se (d5) 		Pa (A4)
Sha (d5)
4 800 Si (A5)
Le (m6) 		Su (A5)
Fla (m6)
5 1000 Li (A6)
Te (m7) 		Lu (A6)
Tha (m7)
6 1200 Do Da

Regular temperament properties

Uniform maps

Lua error in Module:Uniform_map at line 135: Must provide edo if not min or max given..

Commas

6et tempers out the following commas. This assumes val ⟨6 10 14 17 21 22].

Prime
limit 		Ratio[note 2] Monzo Cents Color name Name(s)
3 32/27 [5 -3⟩ 294.13 Wa Pythagorean minor third
5 25/24 [-3 -1 2⟩ 70.67 Yoyo Dicot comma, classic chroma
5 128/125 [7 0 -3⟩ 41.06 Trigu Augmented comma, diesis
5 3125/3072 [-10 -1 5⟩ 29.61 Laquinyo Magic comma, small diesis
5 (12 digits) [17 1 -8⟩ 11.45 Saquadbigu Würschmidt comma
5 (30 digits) [-44 -3 21⟩ 6.72 Trila-septriyo Mutt comma
7 49/48 [-4 -1 0 2⟩ 35.70 Zozo Semaphoresma, slendro diesis
7 50/49 [1 0 2 -2⟩ 34.98 Biruyo Jubilisma, tritonic diesis
7 3136/3125 [6 0 -5 2⟩ 6.08 Zozoquingu Hemimean comma
7 6144/6125 [11 1 -3 -2⟩ 5.36 Sarurutrigu Porwell comma
7 2401/2400 [-5 -1 -2 4⟩ 0.72 Bizozogu Breedsma
11 121/120 [-3 -1 -1 0 2⟩ 14.37 Lologu Biyatisma
11 176/175 [4 0 -2 -1 1⟩ 9.86 Lorugugu Valinorsma
11 385/384 [-7 -1 1 1 1⟩ 4.50 Lozoyo Keenanisma
13 13/12 [-2 -1 0 0 0 1⟩ 138.57 tho 2nd Tridecimal neutral second

Music

Bryan Deister
Chimeratio
  • "Bowser breaks into Arnold Schoenberg's house and steals six of the twelve Tone Crystals (every other one), activating The 666666-Year-Curse Mechanism", from STAFFcirc vol. 7 (2021) – SoundCloud | Bandcamp
Milan Guštar
Aaron Andrew Hunt
NullPointerException Music
Phanomium
Chris Vaisvil
  • The Good Boundless (2011) – blog | play

Notes

  1. ↑ Based on treating 6edo as a subset of 12edo, itself treated as a 2.3.5.7.17.19 subgroup temperament; other approaches are also possible. For example, for 6edo as a 2.5.7.9 subgroup temperament, ignore the "Other" column).
  2. ↑ Ratios longer than 10 digits are presented by placeholders with informative hints.
Retrieved from "https://en.xen.wiki/index.php?title=6edo&oldid=181841"