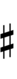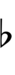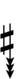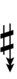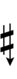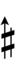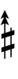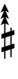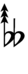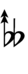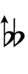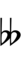49edo

← 48edo

49edo

50edo →

Prime factorization

7²

Step size

24.4898¢

Fifth

29\49 (710.204¢)

Semitones (A1:m2)

7:2 (171.4¢ : 48.98¢)

Dual sharp fifth

29\49 (710.204¢)

Dual flat fifth

28\49 (685.714¢) (→4\7)

Dual major 2nd

8\49 (195.918¢)

Consistency limit

7

Distinct consistency limit

7

49 equal divisions of the octave (abbreviated 49edo or 49ed2), also called 49-tone equal temperament (49tet) or 49 equal temperament (49et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 49 equal parts of about 24.5 ¢ each. Each step represents a frequency ratio of 2^1/49, or the 49th root of 2.

Theory

49edo is very much on the sharp side of things, with sharp tunings of harmonics 3, 5, 7, and 11. It is the optimal patent val for superpyth temperament in the 7- and 11-limit, archytas (7-limit) and ares (11-limit) planar temperaments, being almost exactly equal to 3⁄10-comma superpyth and the e-based analog of Lucy tuning. It tempers out 64/63, 245/243, and 3125/3087 in the 7-limit, and 100/99 and 1375/1372 in the 11-limit.

Harmonics

Approximation of odd harmonics in 49edo
Harmonic		3	5	7	9	11	13	15	17	19	21	23
Error	Absolute (¢)	+8.2	+5.5	+10.8	-8.0	+11.9	-7.9	-10.7	-7.0	-3.6	-5.5	+8.5
Error	Relative (%)	+33.7	+22.6	+44.0	-32.6	+48.8	-32.2	-43.8	-28.6	-14.8	-22.4	+34.5
Steps (reduced)		78 (29)	114 (16)	138 (40)	155 (8)	170 (23)	181 (34)	191 (44)	200 (4)	208 (12)	215 (19)	222 (26)

Subsets and supersets

Since 49 factors into 7², 49edo contains 7edo as its only nontrivial subset. 49edo is the first square edo with a non-enfactored diatonic fifth.

Intervals

#	Cents	Approximate Ratios*	Ups and Downs Notation
0	0.000	1/1	D
1	24.490	50/49	^D, vE♭
2	48.980	28/27, 36/35, 49/48, 81/80	^^D, E♭
3	73.469	22/21, 25/24, 33/32	^³D, ^E♭
4	97.959	16/15, 21/20	v³D♯, ^^E♭
5	122.449	15/14	vvD♯, ^³E♭
6	146.939	12/11	vD♯, v³E
7	171.429	10/9, 11/10	D♯, vvE
8	195.918	28/25	^D♯, vE
9	220.408	8/7, 9/8	E
10	244.898	125/108, 144/125	^E, vF
11	269.388	7/6	F
12	293.878	25/21, 33/28	^F, vG♭
13	318.367	6/5	^^F, G♭
14	342.857	11/9	^³F, ^G♭
15	367.347	27/22	v³F♯, ^^G♭
16	391.837	5/4	vvF♯, ^³G♭
17	416.327	14/11	vF♯, v³G
18	440.816	9/7	F♯, vvG
19	465.306	125/96, 162/125	^F♯, vG
20	489.796	4/3, 21/16	G
21	514.286	75/56	^G, vA♭
22	538.776	15/11, 27/20	^^G, A♭
23	563.265	11/8	^³G, ^A♭
24	587.755	7/5	v³G♯, ^^A♭
25	612.245	10/7	vvG♯, ^³A♭
26	636.735	16/11	vG♯, v³A
27	661.244	22/15, 40/27	G♯, vvA
28	685.714	112/75	^G♯, vA
29	710.204	3/2, 32/21	A
30	734.694	125/81, 192/125	^A, vB♭
31	759.184	14/9	^^A, B♭
32	783.673	11/7	^³A, ^B♭
33	808.163	8/5	v³A♯, ^^B♭
34	832.653	44/27	vvA♯, ^³B♭
35	857.143	18/11	vA♯, v³B
36	881.633	5/3	A♯, vvB
37	906.122	42/25, 56/33	^A♯, vB
38	930.612	12/7	B
39	955.102	125/72, 216/125	^B, vC
40	979.592	7/4, 16/9	C
41	1004.082	25/14	^C, vD♭
42	1028.571	9/5, 20/11	^^C, D♭
43	1053.061	11/6	^³C, ^D♭
44	1077.551	28/15	v³C♯, ^^D♭
45	1102.041	15/8, 40/21	vvC♯, ^³D♭
46	1126.531	21/11, 48/25, 64/33	vC♯, v³D
47	1151.020	27/14, 35/18, 96/49, 160/81	C♯, vvD
48	1175.510	49/25	^C♯, vD
49	1200.000	2/1	D

* Based on 49edo's 11-limit patent val ⟨49 78 114 138 170] mapping

Notation

Ups and downs notation

Using Helmholtz–Ellis accidentals, 49edo can be notated using ups and downs notation:

Step Offset	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Sharp Symbol
Flat Symbol

Sagittal notation

Evo flavor

Revo flavor

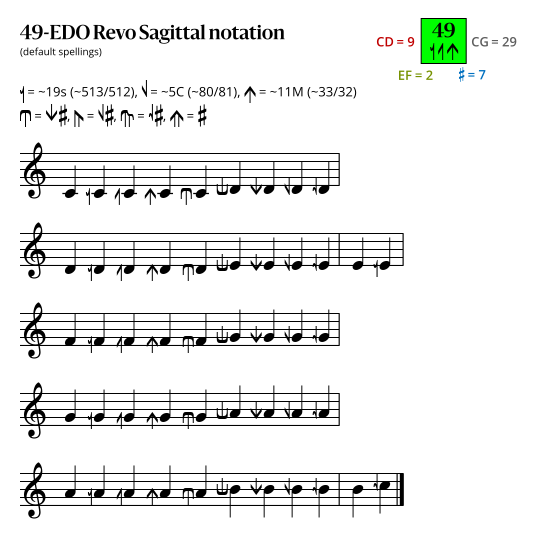
Approximation to JI

Selected 19-limit intervals approximated in 49edo

Interval mappings

The following tables show how 15-odd-limit intervals are represented in 49edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 49edo (direct approximation, even if inconsistent)
Interval and complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
13/9, 18/13	0.117	0.5
11/7, 14/11	1.181	4.8
15/11, 22/15	1.825	7.5
7/6, 12/7	2.517	10.3
5/3, 6/5	2.726	11.1
15/13, 26/15	2.843	11.6
15/14, 28/15	3.006	12.3
11/6, 12/11	3.698	15.1
11/9, 18/11	4.551	18.6
13/11, 22/13	4.668	19.1
7/5, 10/7	5.243	21.4
5/4, 8/5	5.523	22.6
9/7, 14/9	5.732	23.4
13/7, 14/13	5.849	23.9
11/10, 20/11	6.424	26.2
13/8, 16/13	7.875	32.2
9/8, 16/9	7.992	32.6
3/2, 4/3	8.249	33.7
13/12, 24/13	8.366	34.2
15/8, 16/15	10.718	43.8
7/4, 8/7	10.766	44.0
9/5, 10/9	10.975	44.8
13/10, 20/13	11.092	45.3
11/8, 16/11	11.947	48.8

15-odd-limit intervals in 49edo (patent val mapping)
Interval and complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
11/7, 14/11	1.181	4.8
15/11, 22/15	1.825	7.5
7/6, 12/7	2.517	10.3
5/3, 6/5	2.726	11.1
15/14, 28/15	3.006	12.3
11/6, 12/11	3.698	15.1
11/9, 18/11	4.551	18.6
7/5, 10/7	5.243	21.4
5/4, 8/5	5.523	22.6
9/7, 14/9	5.732	23.4
11/10, 20/11	6.424	26.2
13/8, 16/13	7.875	32.2
3/2, 4/3	8.249	33.7
7/4, 8/7	10.766	44.0
9/5, 10/9	10.975	44.8
11/8, 16/11	11.947	48.8
13/10, 20/13	13.398	54.7
15/8, 16/15	13.772	56.2
13/12, 24/13	16.124	65.8
9/8, 16/9	16.498	67.4
13/7, 14/13	18.641	76.1
13/11, 22/13	19.822	80.9
15/13, 26/15	21.647	88.4
13/9, 18/13	24.373	99.5

Zeta peaks

The strongest local zeta peak around 49edo is its second closest, 49.141 edo. One step is 24.419 cents, and two steps, 48.839 cents, is a good generator for Triple BP.

Approximation to irrational intervals

Acoustic ϕ and ϕ^{ϕ^-1}

49edo has a very close approximation of both acoustic phi and ϕ^{ϕ^-1}, a kind of logarithmic phi that divides acoustic phi logarithmically by phi (instead of dividing 2/1).

ϕ^{ϕ^-1} has interesting applications as Metallic MOS, and in particular the fractal-like possibilities of self-similar subdivision of musical scales within acoustic phi.

Direct approximation
Interval	Error (abs, ¢)	#\49
ϕ / ϕ^{ϕ^-1} = ϕ^(2-ϕ)	0.155	13
ϕ	−0.437	34
ϕ^{ϕ^-1}	−0.592	21

Not until 592 do we find a better edo in terms of relative error on these two intervals (but whose edo-steps upon which these intervals are mapped are not based on the Fibonacci sequence, unlike 49edo).

Music

Sevish - Star Nursery uses a scale based on acoustic phi and ϕ^ϕ⁻¹. 49edo provides a suitable approximation for this scale with the mode: 5 3 5 5 3 5 3 5

Regular temperament properties

Subgroup	Comma list	Mapping	Optimal 8ve stretch (¢)	Tuning error
Subgroup	Comma list	Mapping	Optimal 8ve stretch (¢)	Absolute (¢)	Relative (%)
2.3	[78 -49⟩	[⟨49 78]]	−2.60	2.60	10.62
2.3.5	15625/15552, 20480/19683	[⟨49 78 114]]	−2.53	2.12	8.69
2.3.5.7	64/63, 245/243, 3125/3087	[⟨49 78 114 138]]	−2.85	1.92	7.87
2.3.5.7.11	64/63, 100/99, 245/243, 1331/1323	[⟨49 78 114 138 170]]	−2.97	1.74	7.11

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods per 8ve	Generator*	Cents*	Associated ratio*	Temperament
1	1\49	24.5	99/98	Sengagen
1	4\49	98.0	16/15	Passion
1	6\49	146.9	12/11	Bohpier
1	8\49	195.9	28/25	Didacus
1	11\49	269.4	7/6	Infraorwell
1	12\49	293.9	25/21	Kleiboh
1	13\49	318.4	6/5	Catalan
1	16\49	391.8	5/4	Magus
1	17\49	416.3	14/11	Sqrtphi
1	18\49	440.8	9/7	Clyde
1	19\49	465.3	55/36	Semisept
1	20\49	489.8	4/3	Superpyth
7	20\49 (1\49)	489.8 (24.5)	4/3 (250/243)	Sevond (49)
7	20\49 (1\49)	489.8 (24.5)	4/3 (25/24)	Seville (49c)

* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct

Scales

MOS scales

Main article: List of MOS scales in 49edo

Instruments

Lumatone

See Lumatone mapping for 49edo

Music

Mercury Amalgam

Wrong Generation (Demo, January 2022) (2023)

Bryan Deister

Deltarune - Man (cover) (2023)

49edo

Contents