Metallic MOS

Metallic MOS scales are a family of MOS scales generated by metallic means. These scales offer interesting musical possibilities due to special mathematical properties of the metallic means.

In keeping with the grand tradition of prefixing the acronym "MOS" with things that also start with "m" (examples being MODMOS and multi-MOS), Douglas Blumeyer proposes met-MOS as their abbreviation.

The first metallic mean is by far the best known: the golden mean,

[math]\qquad \phi \approx 1.618034 [/math]

Scales based on this mean—or "phi", as it is often called, after the Greek letter used to represent it—are relatively well-known, and these "golden" scales have been described by Erv Wilson, Kraig Grady, David J. Finnamore, Billy Stiltner, Paul Erlich, Graham Breed, Dave Keenan, Margo Schulter, Thorvald Kornerup and many others.

But phi is only the first of an infinite sequence of such metallic means which can be used to generate scales offering interesting musical possibilities. And while some attention has been given to silver scales, what we seek to do here is centralize all met-MOS knowledge and generalize principles across all of the metallic means.

MOS concepts are logarithmic, not acoustic. In other words, we are not dealing with frequency ratios here. Frequency ratios related to metallic means, such as "acoustic phi" (approximately 833.09¢), have interesting properties too—creating recursive combination tones, for example—but these musical applications of metallic means will not be discussed here.

The met-MOS concepts discussed here may be used to define generators as fractions of an octave, as is most common. But these concepts are more abstract than that, and may be used to define generators as fractions of any period. As such, they only depend on the ratio between the generator and the period, and so for convenience we can lock one of these two values to 1 and only vary the value of the other. We'll be conforming here with the convention of choosing the period as the interval to lock to 1.

Since no other types of scales besides MOS scales will be discussed here, we can assume MOS scale whenever we write "scale".

Behavior

In the first part of this discussion we'll go over basic met-MOS behavior, deferring mathematical explanations until later.

Generators

A natural topic to begin with is generators, since we need a generator before we can generate scales.

Golden case

The simplest metallic generator splits the period into two segments which are related by φ. Wilson named this generator "Fibonacci", after the famous recurrence relation associated with φ, but for consistency here we'll be calling this the golden generator.

Noble cases

Another way to think about the period is the interval from 0/1 to 1/1 (these are not frequency ratios, but just another way of writing 0 and 1, the motivation for which will become clear soon). We can find slightly more complex metallic generators by choosing an interval other than the entire period to split into two segments related by φ. For example, we could pick 1/3 to 1/2, giving us approximately 0.419821:

Disclaimer: while these two segments are indeed related by φ, it is not simply by their lengths, as it may appear in the diagram. For now, let it suffice to say that extensions of the golden mean such as this are known as noble numbers. As for why the order of the segments is flipped here—well, that too will be explained later.

Beyond golden cases

So far we've only considered the golden mean. We'll next try the second metallic mean, the silver mean:

[math]\qquad \delta_s \approx 2.414214 [/math]

The silver generator splits the entire period into two segments related by the silver mean, and is approximately equal to 0.292894:

And from the bronze mean,

[math]\qquad \delta_b \approx 3.302776 [/math]

we find the bronze generator, approximately 0.232408:

Isotopic cases

For metallic means beyond golden, a new category of generator becomes available.

Values of the arithmetic progression from the metallic mean downwards by 1 also impart metallic effects when used to split the period to find a generator. The simplest example uses the silver mean minus one,

[math]\qquad \delta_s - 1 \approx 1.414214 [/math]

finding a generator which is approximately 0.414214:

We'll be returning to these values regularly, so for convenience, we'll refer to them as isotopes of their respective metallic mean, e.g. δ_s − 1 is the first isotope of the silver mean (and we'll make no claim as to the scientific appropriateness of this analogy).

Only isotopes greater than 1 find new generators; more on this later.

Isotopes theoretically could be formed by adding 1 repeatedly to each mean, instead of subtracting, but these also do not find new generators, and for simplicity we'll not be considering these to be isotopes at all for our purposes here.

Aristocratic cases

We can find even more metallic generators by extending the concept of noble numbers to metallic means beyond the golden, as well as their isotopes. For example, we could choose the silver mean, and 0/1 to 1/2 as our interval, finding approximately 0.226541:

Since we'll be returning to these types of numbers frequently, for convenience, and by analogy with "noble" numbers, we'll refer to them as aristocratic numbers (and, as before, we'll make no claim as to the sociopolitical accuracy of this analogy).

So, in the end, we have six types of metallic generators. Noble generators and isotopic aristocratic generators can all be referred to as aristocratic generators when the generic category is preferred, although at that point we would probably be even better served to simply use the further generic category "metallic generators":

	Period interval	Non-period interval
Golden mean	Golden generator	Noble generators	Aristocratic generators
Beyond golden mean	Silver generator, bronze generator, etc.	Aristocratic generators
Beyond golden isotope	Isotopic generators	Isotopic aristocratic generators

L:s sequences

Each scale has exactly two step sizes: large and small, or L and s. We can refer to the ratio between these large and small steps as

[math]\qquad L{:}s [/math]

We'll call the ordered set of scales a generator generates its scale sequence, and the ordered set of L:s corresponding to these scales a generator's L:s sequence.

Golden case

The golden generator's L:s sequence is simple. Every L:s ratio is φ:

[math]\qquad L{:}s = \phi [/math]

Noble cases

A noble generator's L:s sequence is slightly more complex. Not every—but almost every—L:s is φ. Only the first few are not.

Beyond golden cases

Instead of every scale's L:s equaling the same value, as is the case for the golden mean, the silver mean's L:s sequence alternates between its isotopes that are greater than 1:

[math] \begin{equation} \begin{cases} \delta_s \\ \delta_s - 1 \\ \end{cases} \end{equation} [/math]

And the bronze mean's L:s sequence cycles through its isotopes that are greater than 1:

[math] \begin{equation} \begin{cases} \delta_b \\ \delta_b - 1 \\ \delta_b - 2 \\ \end{cases} \end{equation} [/math]

Any n-metallic mean's L:s sequence will cycle through its isotopes that are greater than 1.

Isotopic cases

Isotopic L:s sequences are just like those of their mean's, but offset.

For example, the silver mean's first isotope's generator's L:s sequence alternates between L:s = δ_s and L:s = δ_s − 1, just like the silver generator's, however—unlike the silver generator's—it begins with L:s = δ_s − 1.

Aristocratic cases

Again, aristocratic scales synthesize both the complexities of noble scales and beyond golden scales. We'll call the periodic part of an L:s sequence its L:s cycle. So most of the L:s sequence will be the L:s cycle, with only the first few scales not being so.

Interval patterns

As we've seen, the step sizes of metallic scales follow particular patterns. But not just the steps follow patterns—many other intervals of met-MOS scales do too.

Golden case

We know that for golden scales:

[math]\qquad L{:}s = \phi [/math]

But that's not all. Due to the mathemagic of φ, we also get a recursive interval relationship pattern:

[math] \newenvironment{rcases} {\left.\begin{aligned}} {\end{aligned}\right\rbrace} \begin{rcases} L&:s \\ L+s&:L \\ 2L+s&:L+s \\ 3L+2s&:2L+s \\ 5L+3s&:3L+2s \\ &\vdots \\ \end{rcases} = \phi [/math]

Henceforth we'll be referring to these types of recursive interval relationship patterns simply as interval patterns.

Noble cases

Noble scales at first do not—but eventually do—reach a point where they start exhibiting this interval pattern (paralleling how their L:s sequences only eventually exhibit L:s = φ).

Once we've iterated past the point that our scale exhibits L:s = φ, some of the smaller intervals will begin to be related by φ, but its larger intervals will never be related by φ.

Beyond golden cases

The silver generator, as it did for its L:s sequence, alternates in quality between its two >1 isotopes for its intervals. For half of its scales,

[math] \newenvironment{rcases} {\left.\begin{aligned}} {\end{aligned}\right\rbrace} \begin{rcases} L&:s \\ 2L+s&:L \\ 5L+2s&:2L+s \\ 12L+5s&:5L+2s \\ 29L+12s&:12L+5s \\ \vdots \\ \end{rcases} = \delta_s [/math]

and the other half,

[math] \newenvironment{rcases} {\left.\begin{aligned}} {\end{aligned}\right\rbrace} \begin{rcases} L&:s \\ L+2s&:L+s \\ 3L+4s&:2L+3s \\ 7L+10s&:5L+7s \\ 17L+24s&:12L+17s \\ \vdots \\ \end{rcases} = \delta_s - 1 [/math]

Bronze's scales cycle through three different interval patterns related to its respective [math]\gt 1[/math] isotopes.

This pattern continues for other metallic means. As another entry to our family of sequence terms (along with scale sequence and L:s sequence) we shall use the term interval pattern sequence, and for the periodic part at the end, the interval pattern cycle.

Isotopic cases

As with L:s sequences, isotopic interval pattern sequences are identical to their metallic mean's, cycling through a set of interval patterns from the beginning, except starting at a different position in that cycle.

Aristocratic cases

Predictably, the aristocratic case combines the noble case and the beyond golden cases: at first, the ratios do not exhibit interval patterns, but eventually they do, and when they start to, they follow the interval pattern cycle for the appropriate metallic mean or isotope thereof.

Mathematical explanations

We'll now start going through mathematical explanations for the behavior we've observed about met-MOS generators, L:s sequences, and interval patterns.

Infinite scale sequences

Every metallic generator generates an infinitely long scale sequence.

This property is not unique to metallic generators, though—it is attributable to their being irrational numbers. A rational generator's scale sequence eventually terminates, hitting bedrock when the period has been divided up into equal steps, i.e. where the notion of large steps and small steps no longer applies because L = s and L:s = 1. For example, the generator

[math]\qquad \frac{5}{12} = 0.41\overline{6} [/math]

generates scales with cardinality 2, 3, 5, 7, but when it reaches cardinality 12, it has generated 12edo. This occurs exactly at the moment when the generator has been repeated until it has returned exactly to from where it started (because 5/12 · 12 = 5, which is a multiple of the period, 1); if we repeated the generator any more, we'd just go over the ground we already trod.

Irrational generators will never be able to return to exactly from where they started, so they will continue to divide the period up into smaller and smaller steps forever. At some point, however, the scales they generate will cease to be musically practical, because their steps will have become so small.

What is special about metallic generators' infinite scale sequences—as opposed to those of other irrational generators—is that no matter how infinitesimally small their steps become, they will maintain their metallic ratios to each other.

The ratio L:s = φ is unique in that it is the only ratio in which the MOS is strictly proper, and all of its descendent MOS's are also strictly proper.

Weighted mediants

As the formula for generators

Recall that in order to find a metallic generator, we find a value which splits an interval into two segments related by a metallic mean. When this technique was introduced earlier, we left the definition of "related by" vague. Well, now is the time to make it explicit.

In our very first case—that of the golden generator—"related by" could be defined as simply "having a ratio of". We'll check the segment lengths to confirm this. One of the two segments is, of course, equal to the golden generator, approximately 0.381966. The other is equal to the remainder of the golden generator with the period:

[math]\qquad 1 - 0.381966 = 0.618034 [/math]

And as we can see, the ratio between those two lengths is φ:

[math]\qquad \frac{0.618034}{0.381966} \approx \phi [/math]

However enticingly simple this definition may be, it unfortunately does not work in general. In fact, it only gives the correct value when the interval being split is the entire period.

The correct general definition of a metallic generator is actually a mediant of the two ratios which bound the interval.

But even then it's not quite that simple, because it's not a simple mediant between a₁/a₂ and b₁/b₂, which would look like this:

[math]\qquad \frac{a_1 + b_1}{a_2 + b_2} [/math]

Rather, it's a weighted mediant, where the weight is w₁/w₂, which looks like this:

[math]\qquad \frac{a_1w_1 + b_1w_2}{a_2w_1 + b_2w_2} [/math]

In particular, it is the mediant which is weighted by the desired metallic mean μ:

[math]\qquad \frac{a_1\mu + b_1}{a_2\mu + b_2} [/math]

In some materials, the weighted mediant between two ratios using φ as the weight is referred to as the value "phi-way" between these two ratios. This analogy with the word "halfway" is misleading, because while the value halfway between two ratios splits the length into two segments which each are half of the total length, with the weighted mediant, the value splits the length into two segments neither of which is φ of the total length. In fact, that would not be possible, because while half is less than one, φ is greater than one, and part of a length can never be greater than the whole length. An alternative phrasing could be: the value φ-weighted from a₁/a₂ to b₁/b₂; besides eschewing the misleading association with "halfway", another advantage of this nomenclature is its ability to specify, via the from/to, which direction the mediant is weighted. Another potential name for this construct is the "phidiant" (or "φ-diant") from a₁/a₂ to b₁/b₂, which is especially nice if you a person who pronounces φ like /fiː/ (the same as "fee").

As a bizarro average

We can think of a mediant like a bizarro average of two ratios: however we may choose to weight one, it will always lie somewhere between the two ratios. That is why we can call these two ratios its bounds. This fact is easy enough to intuit: as the weight tends toward zero, the effects of a₁ and a₂ drops off to nothing, and as it tends toward infinity, their effects begin to utterly overwhelm b₁ and b₂.

[math] \begin{align} \lim_{w\to 0} \frac{a_1w + b_1}{a_2w + b_2} &= \frac{b_1}{b_2} \\ \lim_{w\to \infty} \frac{a_1w + b_1}{a_2w + b_2} &= \frac{a_1}{a_2} \end{align} [/math]

Checking our earlier results

To confirm that the weighted mediant formula gives the same result for the golden generator as we were using before, we can plug in 0/1 and 1/1 for our bounds:

[math]\qquad \frac{1\phi + 0}{1\phi + 1} \approx 0.618034 [/math]

And finally we can show how we got approximately 0.419821 as the value for the noble generator between 1/3 and 1/2:

[math]\qquad \frac{1\phi + 1}{2\phi + 3} \approx 0.419821 [/math]

About diagram labels

In the generator diagrams earlier in this discussion—as we disclaimed at that time—the labels on the segments were not indicating length. We know now that what they were actually indicating was the mediant weight. For our purposes, mediant weight is more helpful information, so we're going to continue labeling the segments this way.

Stern–Brocot tree

As interval finder

We've left still another part about our instructions for finding metallic generators vague: the "an interval" part. It turns out that not just any interval can yield a metallic generator—only those whose bounding ratios are sequential convergents (or semiconvergents) of a continued fraction.

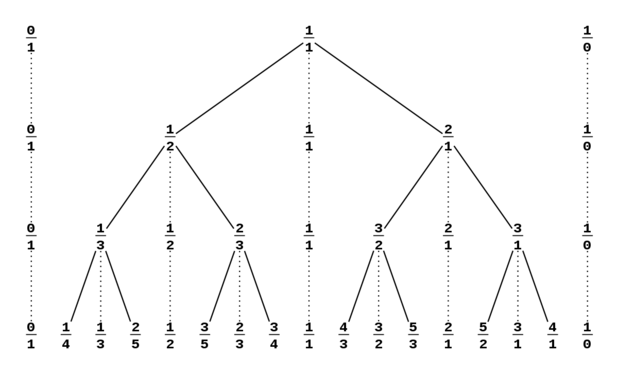
Now that's a mouthful, to be sure—but we don't need to understand what that entails at this point, because it can easily be tested by checking that a₁b₂ − a₂b₁ = ±1. And fortunately for us, an algorithm called the Stern–Brocot tree graphs all of these intervals for us:

As we can see, Stern–Brocot trees actually cover ratios greater than 1, but for met-MOS purposes, we only need to consider the left half of it (in fact, we only need to consider the left quarter of it, since generators greater than 1/2 are complements of those less than 1/2 and generate the same scales; but more on that later).

So to quickly find a unique metallic generator, we only have to choose a ratio from the tree, and then choose either one of its two parent ratios; the line connecting these two ratios will be our interval.

Finding by child ratio

Finding by the child ratio is helpful when reasoning about the levels of the tree and its intervals. It's just good recursive design.

We'll present a counterexample. If we instead followed the policy of finding by the parent ratio, choosing it as our first ratio and then choosing one of its child ratios to define our interval, then we'd always have to consciously avoid choosing ratios from the currently deepest level, because we wouldn't be able to use those without recursing the tree another level.

But if we follow the policy of finding by the child ratio first and then the parent ratio, we only have to avoid the currently shallowest level of the tree. This is much easier, because:

1. It never changes—it's always at the root of the tree;
2. It's much smaller, including only a single ratio, 0/1;
3. That single ratio doesn't even have a parent ratio anyway, so it's easy to avoid.

Another benefit of finding by the child ratio is that every ratio has exactly two parent ratios, while its count of child ratios is variable (consider how many child ratios 0/1 has).

Each interval spans two levels of the tree, because a parent ratio will always be one level less than its child ratio. When classifying intervals by level, then, we should classify them by the child ratio. For example, we should consider the interval 1/7 to 1/6 a seventh-level interval, because it would not be available until we included the seventh level.

By the way, here is an easy way to identify which level of the tree a ratio is on: we can scan along the level to the left until we find the unit fraction which appears in the initial position, closest to 0/1; if our level starts with 1/n, then the ratio is in the n_th level.

Interval lean

Each interval in the Stern–Brocot tree offers two leans: parentward, and childward.

This concept is completely orthogonal to the points made in the previous section. The previous section was about choosing an interval. This section is about—once an interval has been chosen—one option we have for how to treat it.

This option is which of the two bounding ratios of the interval receives the weight in the weighted mediant formula. When weighted parentward, it's the parent ratio that receives the weight, and vice versa for childward.

For example, we'll look at our noble generator example again. This one is weighted parentward,

[math]\qquad \frac{1\phi + 1}{2\phi + 3} \approx 0.419821 [/math]

because—of its two bounding ratios, 1/2 and 1/3—the parent is 1/2.

We could weight childward instead though:

[math]\qquad \frac{1 + 1\phi}{2 + 3\phi} \approx 0.381966 [/math]

which, interestingly, gives us the same value as the golden generator.

In Wilson's work, he only used childward lean; had he included parentward lean for his noble generators, he would have found every single generator in one earlier level of the tree than he had previously. For example, he names the golden generator, leaning toward 1/2, which of the two ratios is the child:

[math]\qquad \frac{1\phi + 0}{2\phi + 1} \approx 0.381966 [/math]

whereas we would name it, leaning toward 0/1, which of our two ratios is the parent:

[math]\qquad \frac{0\phi + 1}{1\phi + 1} \approx 0.381966 [/math]

Levels of metallicity

The Stern–Brocot tree can be recursed indefinitely, so an infinite number of metallic generators exist. And since each parent ratio branches into two child ratios, each new recursive level of the Stern–Brocot tree offers the next power of 2 more intervals.

Despite this exponential profusion of scales, however, as one travels deeper down the tree, the generators lose musical interest. They become less and less metallic. We can quantify their metallicity in terms of how many iterations of their scale sequence are required before they reach the scale which

1. begins the periodic phase of the L:s sequence for the metal they're based on, and
2. begins supporting the interval pattern for the metal they're based on.

The golden generator is essentially the noble generator for the interval 0/1 to 1/1, which—being the root of the Stern–Brocot tree—is as golden as we can get: we see L:s = φ and φ's distinctive interval pattern from the very start.

And the noble generator between 0/1 and 1/3

[math]\qquad \frac{1\phi + 0}{3\phi + 1} \approx 0.276393 [/math]

is very close to the root of the tree; it has initial L:s ratio of [math]\phi + 2[/math], then attains L:s = φ after only one iteration. And it begins the golden interval pattern after just one iteration too.

On the other hand, the noble generator equal to 0.275267—while only a smidgen off from the other noble generator we just looked at—necessitates iterating six times before attaining L:s = φ. This corresponds to it being the noble generator between [math]\frac {5}{18}[/math] and [math]\frac {3}{11}[/math], an interval which lies five levels deeper in the Stern–Brocot tree than the interval from 0/1 to 1/3.

So if we want a golden scale, and we also happen to want a generator near 0.276393, then we're in luck. But if we want a golden generator that is close to 0.275267, we may be disappointed to hear that it is not "golden" enough for us.

Wilson documented noble scale sequences through the seventh level of the Stern–Brocot tree (or as he called it, the "scale tree" or "Peirce Series"), totaling 64 noble generators. He also recorded just the generator values down to the eleventh level for a total of 1024 generators. Exploring generators beyond that was probably just not worth it, because their metallicity levels are too low. We will cut ourselves off at the seventh level in our scale trees, as we depict generators for the silver and bronze means, and their isotopes too.

Naming generators

While not every interval can make a noble number, every noble number can be found as the weighted mediant of many intervals. For example,

[math]\qquad 0.216542 \approx \frac{0\phi + 1}{1\phi + 3} \approx \frac{1\phi + 0}{4\phi + 1} \approx \frac{2\phi + 1}{9\phi + 5} \approx … [/math]

This ambiguity presents a naming problem. Naming generators after combinations of an interval and the metallic value used in the weighted mediant formula definitely makes sense, but we need to know which of these possibilities to choose.

The solution is simple: choose the earliest level in the tree where the generator appears. There will be only one possible way to express the generator in each level (e.g. it is not possible for one generator to be found by both the silver mean and its first isotope in the same interval), so no further decisions will need to be made.

This solution will result in some generators being named for metallic means and others for isotopes. It will also result in some generators being named for parentward intervals and others for childward ones. We suggest this inconsistency is worth the otherwise simplicity of the solution.

Generator complements

Generators are equivalent to their complements:

[math]\qquad g ≡ 1 - g [/math]

By "equivalent", we mean that they will generate essentially the same scale sequence. And by "essentially the same" we mean that the scales will be mirror images of each other, which for an MOS scale, happens to also mean that they are simply transpositions of each other (different modes of the same scale).

As for why we pick the lower half of the period rather than the upper half, this is somewhat arbitrary, but it seems objectively simpler to keep our lower bound at 0.

Sure, depending on the context, the generator complement greater than 0.5 may be the one we want to describe our scale in terms of. For example, we may be thinking of the generator as the perfect fifth instead of the perfect fourth. Or we may want to use 0.618034 instead of its complement 0.381966 (we've been using the latter and calling it the golden generator, but some readers may be more familiar with the former, known as "logarithmic phi", which is 741.64¢ when the period is an octave). But for purposes of cataloging we prefer the smaller, or reduced of the two complements.

And this is a subtle point, but it's another reason to prefer leaning intervals parentward. We have a potential problem: we don't want to find generators [math]\gt 0.5[/math]. Almost every interval we include does not even allow for that possibility, but one interval does threaten this: the interval 0/1 to 1/1. We include this interval because it occupies space between 0/1 and 1/2—so has potential to find useful generators—but we have to be careful with it to avoid finding generators [math]\gt 0.5[/math]. The method for this is simple. First, note that the unweighted mediant in the interval 0/1 to 1/1 is 1/2, or exactly 0.5. So if we want to avoid generators [math]\gt 0.5[/math], all we must do is make sure to weight more toward 0/1. Since of these two ratios 0/1 and 1/1, the parent ratio is 0/1, weighting parentward is the solution.

Isotopic arithmetic progression

Now we'll explain why the L:s sequences for metallic means cycle through their isotopes.

Why they decrease by 1

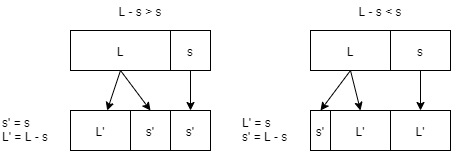
First we need to review some MOS concepts. The mechanics of scale generation are such that—when iterating from one scale to the next densest one—all large steps in the preceding scale become one large step and one small step in the new scale.

Another way to think about this is that a small-step-sized chunk has been split off of each of the former large steps. The remainder can be either larger or smaller than the small step. If it is larger, then it stays the large step. If it is smaller, then it becomes the new small step, and everything that used to be a small step is now a large step.

We are reasoning about MOS concepts in the abstract here. These truths about large and small steps are true whether they are 100¢ or 4516.8¢, and all we really care about are their ratios. So if we treat our small steps' size as 1 then we can treat our large steps' size as equal to the L:s ratio.

So the L:s ratio decreases by 1 because if an s-sized chunk has been sliced off [math]L[/math], and [math]s[/math]'s size is 1, then 1 should be subtracted from [math]L[/math].

[math] \begin{align} L'{:}s' &= (L - s){:}s \\ &= (L - 1){:}1 \\ &= L - 1 \end{align} [/math]

Why they cycle

That is true of scale iterations where L − s > s. For the other type of scale iteration, where L − s < s, the result is simply reciprocated:

[math] \begin{align} L'{:}s' &= s{:}(L - s) \\ &= 1{:}(L - 1) \\ &= \frac{1}{L - 1} \end{align} [/math]

This alone would not suffice to explain how the L:s sequences lock into a cycle of isotopes. But here's where the magic of the metallic means comes into play. φ has the property that

[math]\qquad \phi - 1 = \frac{1}{\phi} [/math]

So, in the case of φ:

[math] \begin{align} L'{:}s' &= \frac{1}{L - 1} \\ &= \frac{1}{\phi - 1} \\ &= \frac{1}{\frac{1}{\phi}} \\ &= \phi \end{align} [/math]

That's why the golden L:s sequence locks into L:s = φ forever.

A similar case is true for the silver mean, except we have to subtract 1 from it twice before the resulting value's reciprocal is equal to the silver mean.

[math]\qquad \delta_s - 1 - 1 = \frac{1}{\delta_s} [/math]

And for the bronze ratio, we must subtract thrice:

[math]\qquad \delta_b - 1 - 1 - 1 = \frac{1}{\delta_b} [/math]

Basically, we are subtracting 1 from the means until only their decimal part remains. One way to describe the metallic means, then, would be the set of values for which the reciprocal of their decimal part equals themselves.

Why the < 1 isotopes do not work for finding generators

And that is why the isotopes less than 1 do not work for finding generators: they are redundant with their respective metallic mean.

For example, the golden mean does have an isotope, [math]\approx 0.618034[/math], however, because the golden mean minus one is the same as the inverse of the golden mean,

[math]\qquad 1{:}\phi = (\phi - 1){:}1 [/math]

we've ended up splitting the period up into segments of the same length, just swapped which one is on which side.

Continued fractions

An understanding of continued fractions unlocks many insights about metallic means, and also many insights about MOS scales, so it should be no surprise that they are particularly rife with insights about met-MOS scales, the intersection of the two concepts.

Behavior

First we'll document some behavior of continued fractions. Then we'll get into applications.

The metallic means are all irrational numbers. Therefore their continued fractions are infinite, with a periodic pattern at the end. An advantage of continued fractions over the decimal system is that we can easily determine whether a number is rational by whether a periodic pattern at the end is required. Decimals, on the other hand, sometimes require periodic patterns at the end even when the number is rational, such as 1/3 which is [math]0.\overline{3}[/math], or 1/7 which is [math]0.\overline{142857}[/math]; as continued fractions these two values are, respectively, [math][0; 3][/math] and [math][0; 7][/math].

The golden mean has the continued fraction [math][1; \overline{1}][/math]. The larger a term in a continued fraction, the closer the approximation of the value at that point; by this conception of irrationality, the golden mean is sometimes said to be the most irrational number possible, eluding close approximation by any ratio as much as possible at every turn.

The silver mean follows it closely with continued fraction [math][2; \overline{2}][/math], and the bronze mean with [math][3; \overline{3}][/math].

A handy way to quickly find the reciprocal of a number is to prepend its continued fraction with a 0. So, we can find the golden mean's isotope 0.618034 is [math][0; \overline{1}][/math].

Actually any isotope's continued fraction is found by simply depleting the initial term. For example, the silver mean's isotopes are [math][1; \overline{2}][/math] and [math][0; \overline{2}][/math]. The initial term of a continued fraction, the one to the left of the semicolon, carries the same information as the digit of a decimal just to the left of the decimal point, i.e. any number starting with [math][0;][/math] is between 0 and 1.

The continued fraction for any abstract generator should start with 0, then, because it must be less than the period, which is 1 (if not less than 0.5, as we've been preferring, because of the generator complement effect).

Noble generators start with other numbers but then settle on all 1's; for example, our earlier example of 0.419821 is [math][0; 2, 2, \overline{1}][/math].

Crossing nobles with beyond golden cases results in continued fractions which can start with anything but eventually settle on all 2's, 3's, or [math]n[/math] if we base our noble on the [math]n[/math]th metallic mean. For example, our earlier example 0.226541 is [math][0; 4, \overline{2}][/math]

Application: L:s sequences

Continued fractions can compute L:s sequences by repeatedly depleting the terms of the continued fraction for the generator. For example, we'll look at the L:s sequence for [math]g = [0; 2, 2, \overline{1}] \approx 0.419821[/math].

[math] L{:}s =\begin{align} \begin{cases} [2; 2, \overline{1}] &\approx 2.381966 \\ [1; 2, \overline{1}] &\approx 1.381966 \\ [2; \overline{1}] &\approx 2.618034 \\ [1; \overline{1}] &\approx 1.618034 = \phi \\ &\vdots \end{cases} \end{align} [/math]

We've stated that L:s = φ for every golden scale, while L:s for noble scales eventually do, just not at first. Noble L:s sequences lock onto φ at the point where depleting the continued fraction more no longer changes it (removing a 1 from the beginning of an infinite string of 1's is a no-op).

Thus it makes sense that logarithmic phi's L:s sequence remains fixed from the beginning, because with a continued fraction of [math][0; 1][/math] we get the L:s sequence

[math] L{:}s =\begin{align} \begin{cases} [1; \overline{1}] &\approx 1.618034 = \phi \\ &\vdots \end{cases} \end{align} [/math]

And it makes sense that the silver mean's generator would alternate between two L:s ratios, because it will alternate between

[math] L{:}s =\begin{align} \begin{cases} [2; \overline{2}] &\approx 2.414214 = \delta_s \\ [1; \overline{2}] &\approx 1.414214 = \delta_s - 1 \\ &\vdots \end{cases} \end{align} [/math]

Application: finding generator

To compute the L:s sequence, we depleted terms of the generator's continued fraction. By doing the opposite—gradually building up the generator's continued fraction by incrementing terms—we can determine the path our generator takes through the Stern–Brocot tree.

We'll use the example of the golden generator, with continued fraction [math][0; 2, \overline{1}][/math]:

[math] \begin{align} \begin{cases} [0; 1] &= \frac{1}{1} \\ [0; 2] &= \frac{1}{2} \\ [0; 2, 1] &= \frac{1}{3} \\ [0; 2, 1, 1] &= \frac{2}{5} \\ [0; 2, 1, 1, 1] &= \frac{3}{8} \\ [0; 2, 1, 1, 1, 1] &= \frac{5}{13} \\ &\vdots \end{cases} \end{align} [/math]

If we look at the path that the generator [math]\approx 0.381966[/math] takes through the scale tree—which intervals it crosses between as it goes—we'll see that they are precisely the intervals bounded by these ratios, in this order.

Perhaps an even better way to approach the problem is to consider the terms of the continued fraction as map directions through the scale tree: each term represents a count of steps one should go in one direction, left or right, before switching directions. We start at 1/1, going left twice to 1/2 and then to 1/3. Then we go right once to 2/5. Then we go left once to 3/8, and right once to [math]\frac{5}{13}[/math], and we can continue onwards.

Application: finding tree level

The sum of the terms of any continued fraction in the Stern–Brocot tree is equal to its level in the tree. For example, the fifth level of the tree consists of 1/5, 2/7, 3/8, and 3/7:

[math] \begin{align} \frac 15 &= [0; 5], &0 + 5 &= 5 \\ \frac 27 &= [0; 3, 2], &0 + 3 + 2 &= 5 \\ \frac 38 &= [0; 2, 1, 2], &0 + 2 + 1 + 2 &= 5 \\ \frac 37 &= [0; 2, 3], &0 + 2 + 3 &= 5 \\ \end{align} [/math]

μ notation

A number of names and symbols have historically been used to denote metallic means. But many of them are ambiguous, or outright conflict with each other, and unfortunately none of them are optimal for met-MOS purposes. We've gotten by alright so far using traditional names and symbols in this discussion, but for the master charts we're going to need to break from tradition in order to most clearly convey the patterns therein. So, we here propose a new notation using the Greek letter μ, read "mu" (μ because "m" figures so prominently in this domain: "m" for metallic, mean, or moment).

This μ notation is a direct approximation of the continued fraction for the metallic mean or isotope, as can clearly be seen in the following chart.

Our name	Common names	Common symbols	Decimal approximation	Continued fraction	μ form	σ form	Ratio
—	—	—	1	[math][1; \overline{0}][/math]	[math]{}_{1}\mu_{0}[/math]	[math]\sigma_1^0[/math]	[math]\frac{0 + \sqrt{4}}{2}[/math]
Golden mean	Phi, golden ratio, golden section, golden proportion, greater phi, divine proportion, Phi	φ, φ, τ, σg	1.618034…	[math][1; \overline{1}][/math]	[math]{}_{1}\mu_{1}[/math]	[math]\sigma_1^1[/math]	[math]\frac{1 + \sqrt{5}}{2}[/math]
Golden mean's isotope	Lesser phi, golden ratio conjugate, silver ratio, phi	φ	0.618034…	[math][0; \overline{1}][/math]	[math]{}_{0}\mu_{1}[/math]	[math]\sigma_{-1}^1[/math]	[math]\frac{-1 + \sqrt{5}}{2}[/math]
Silver mean	Silver ratio	δs, σs	2.414214…	[math][2; \overline{2}][/math]	[math]{}_{2}\mu_{2}[/math]	[math]\sigma_2^1[/math]	[math]\frac{2 + \sqrt{8}}{2}[/math]
Silver mean's first isotope	Japanese mean, silver ratio	[math]\sqrt{2}[/math]	1.414214…	[math][1; \overline{2}][/math]	[math]{}_{1}\mu_{2}[/math]	[math]\sigma_0^2[/math]	[math]\frac{0 + \sqrt{8}}{2}[/math]
Silver mean's second isotope	—	—	0.414214…	[math][0; \overline{2}][/math]	[math]{}_{0}\mu_{2}[/math]	[math]\sigma_{-2}^1[/math]	[math]\frac{-2 + \sqrt{8}}{2}[/math]
Bronze mean	—	δb, σb	3.302776…	[math][3; \overline{3}][/math]	[math]{}_{3}\mu_{3}[/math]	[math]\sigma_3^1[/math]	[math]\frac{3 + \sqrt{13}}{2}[/math]
Bronze mean's first isotope	—	—	2.302776…	[math][2; \overline{3}][/math]	[math]{}_{2}\mu_{3}[/math]	[math]\sigma_1^3[/math]	[math]\frac{1 + \sqrt{13}}{2}[/math]
Bronze mean's second isotope	—	—	1.302776…	[math][1; \overline{3}][/math]	[math]{}_{1}\mu_{3}[/math]	[math]\sigma_{-1}^3[/math]	[math]\frac{-1 + \sqrt{13}}{2}[/math]
Bronze mean's third isotope	—	—	0.302776…	[math][0; \overline{3}][/math]	[math]{}_{0}\mu_{3}[/math]	[math]\sigma_{-3}^1[/math]	[math]\frac{-3 + \sqrt{13}}{2}[/math]

Interval pattern recursion

Earlier we observed the interval patterns of met-MOS scales. Now we'll explain why they are recursive in the way that they are.

Golden case

We know that the golden generator's L:s = φ, but we can also say this about them:

[math]\qquad (L+s){:}L = \phi [/math]

In other words, any interval in the scale which spans exactly one large and one small step is φ times the size of one large step.

This fact follows from one of the many ways of defining the golden mean: the value for which

[math]\qquad a{:}b = (a+b){:}a = \phi [/math]

We can substitute into this equation our large and small scale step sizes in place of a and b, respectively, to see that

[math]\qquad L{:}s = (L+s){:}L = \phi [/math]

But we're only getting started. This situation has recursive potential. We can now substitute [math]L+s[/math] in for [math]L[/math] as long as we also substitute in L for s, and we'll still get a ratio that equals φ:

[math] \begin{align} ((L+s)+(L)){:}(L+s) &= \\ (2L+s){:}(L+s) &= \\ \phi \end{align} [/math]

Continuing this recursive process, the case will be that

[math] \newenvironment{rcases} {\left.\begin{aligned}} {\end{aligned}\right\rbrace} \begin{rcases} L&:s \\ L+s&:L \\ 2L+s&:L+s \\ 3L+2s&:2L+s \\ 5L+3s&:3L+2s \\ &\vdots \end{rcases} = \phi [/math]

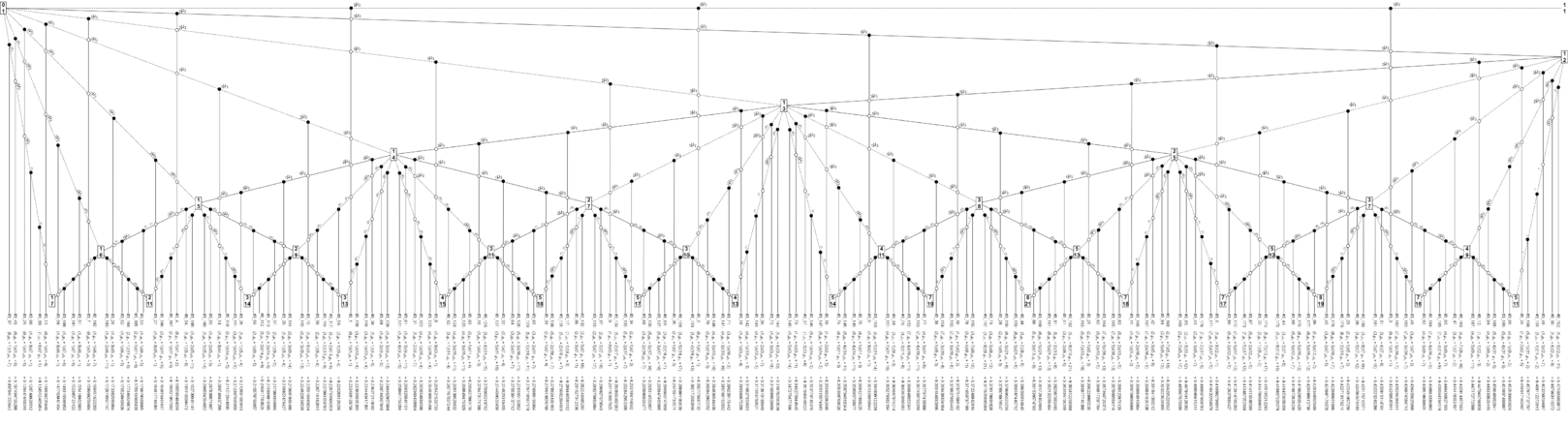
We can visualize the interval pattern using what is called a horogram:

Horogram for g ≈ 0.381966, 7 iterations

Horograms depict the scale sequences of MOS generators. To understand how the horogram illustrates the interval pattern, too, first consider just the left side of the interval pattern, for L:

[math] \begin{aligned} L \\ L+s \\ 2L+s \\ 3L+2s \\ 5L+3s \\ \vdots \end{aligned} [/math]

Now find any L in the horogram and observe how it gets split up as we iterate through the scale sequence. In the next iteration, [math]L[/math] will be replaced with an L and an s. After two iterations, the original L interval is now represented by two L's and an s. And so forth.

The same will hold for the right side of the interval pattern, for s:

[math] s \\ L \\ L+s \\ 2L+s \\ 3L+2s \\ \vdots [/math]

Find any [math]s[/math] in the horogram and observe how it gets split up as we iterate through the scale sequence. In the next iteration, s will be replaced with L. After two iterations, the original s interval is now represented by an L and an s. And so forth.

Every MOS scale contains every scale earlier in its scale sequence. In other words, any interval that existed in an earlier scale will remain in all later scales. These earlier L's and s's that remain—only now spanning many L's and s's each—are precisely the larger intervals in the scale that also exhibit the φ ratio to each other.

Beyond golden cases

If the golden mean is the value for which a:b = (a + b):a, then the silver mean is the value for which

[math] a{:}b = (2a+b){:}a = \delta_s [/math]

Following the same logic as we followed for the golden case,

[math] L{:}s = (2L+s){:}L = \delta_s [/math]

So, wherever we have a scale where L:s = δ_s, we'll also see the interval pattern

[math] \newenvironment{rcases} {\left.\begin{aligned}} {\end{aligned}\right\rbrace} \begin{rcases} L&{:}s \\ (2L+s)&{:}L \\ (5L+2s)&{:}(2L+s) \\ (12L+5s)&{:}(5L+2s) \\ (29L+12s)&{:}(12L+5s) \\ &\vdots \end{rcases} = \delta_s [/math]

Every other scale the silver generator generates has an L:s other than δ_s, namely, its isotope, δ_s − 1. These scales have a different pattern:

[math] L{:}s = (L+2s){:}(L+s) = \delta_s - 1 [/math]

Due to this different pattern, we'll see the different interval pattern

[math] \newenvironment{rcases} {\left.\begin{aligned}} {\end{aligned}\right\rbrace} \begin{rcases} L&{:}s \\ (L+2s)&{:}(L+s) \\ (3L+4s)&{:}(2L+3s) \\ (7L+10s)&{:}(5L+7s) \\ (17L+24s)&{:}(12L+17s) \\ &\vdots \end{rcases} = \delta_s - 1 [/math]

horogram for g = 0.292893, 7 iterations

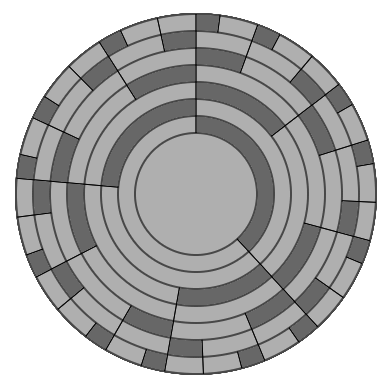
We can use the horogram for the silver generator to see how its interval pattern cycle is length 2, i.e. that it alternates between two different interval patterns. If we want to understand the interval pattern for δ_s, we'll look at the right and left sides separately, as we did with the golden:

[math] \begin{aligned} L \\ 2L+s \\ 5L+2s \\ 12L+5s \\ 29L+12s \\ \vdots \\ \end{aligned} [/math]

[math] s \\ L \\ 2L+s \\ 5L+2s \\ 12L+5s \\ \vdots \\ [/math]

We'll repeat the technique we used for the golden case: find any [math]L[/math] in the horogram and observe how it gets split up as we iterate through the scale sequence. However, the complexity that silver introduces is that we don't look to the next iteration to see the next entry in the interval pattern; we have to skip an iteration. So if we just look at all the odd rings, ring 1, 3, 5, 7, etc. then we'll see the pattern. The same is true of s.

And if we want to understand the interval pattern for δ_s − 1, we'll look at the right and left sides separately:

[math] \begin{aligned} L \\ L+2s \\ 3L+4s \\ 7L+10s \\ 17L+24s \\ \vdots \\ \end{aligned} [/math]

[math] s \\ L+s \\ 2L+3s \\ 5L+7s \\ 12L+17s \\ \vdots \\ [/math]

And now we'll look not at the odd, but at the even iterations, rings 2, 4, 6, 8, etc. to see the pattern visualized.

There's something a bit different about the interval pattern for δ_s − 1 from the other two we've looked at so far. The interval patterns for δ_s and φ exhibited overlap, i.e. we saw something like

[math] a{:}b = b{:}c = c{:}d = … = \delta_s [/math]

here we do not see such overlapping; the pattern of intervals looks more like

[math] a{:}b = c{:}d = e{:}f = … = \delta_s - 1 [/math]

The reason the other cases exhibited such overlapping is that the small step size of the next ratio in the equivalence pattern became an L, which is the same as the L size of the preceding ratio. However, for the silver mean's first isotope here, no such link exists, since s is substituted not for L, but L + s.

Another way of looking at this is: for δ_s and φ, it was the case that both [math]s[/math] and [math]L[/math]'s interval sequences were the same, just offset from each other by a step. Whereas for δ_s − 1,s and L's interval sequences are completely different.

Finally, for the bronze ratio,

[math] a{:}b = (3a+b){:}a [/math]

As expected, L:s = (3L + s):L is only true of every third scale the bronze generator generates. The remaining interval relationships are left as an exercise for the reader.

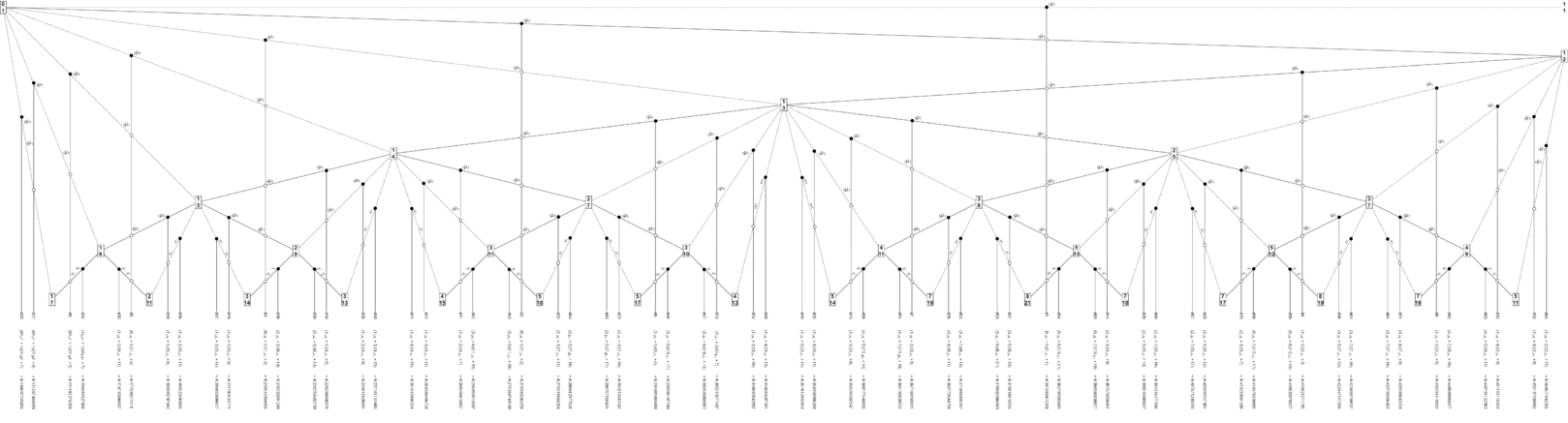
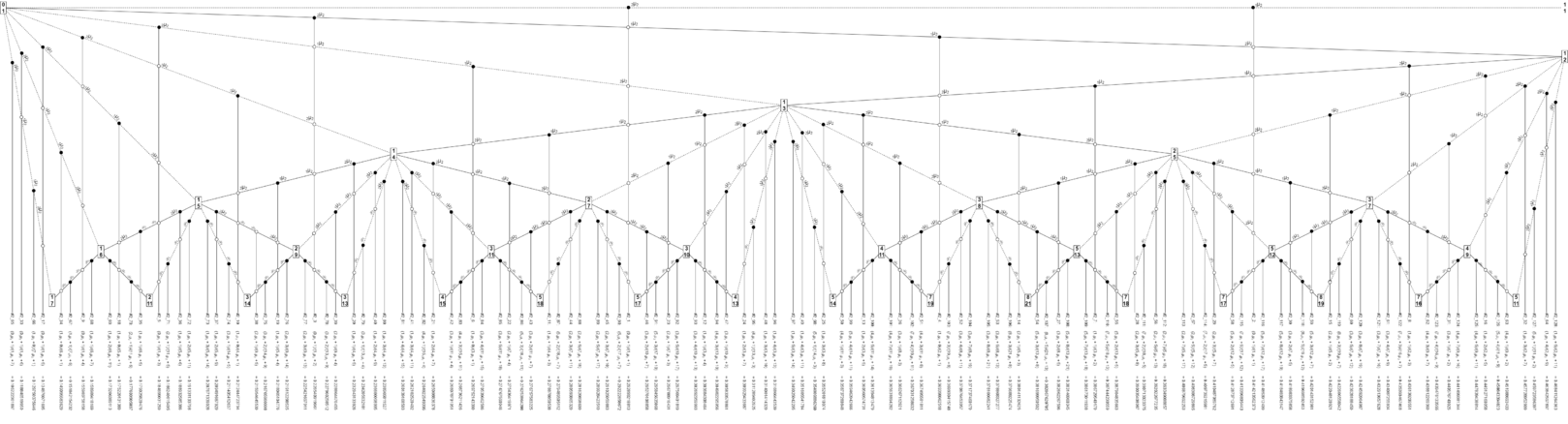
Gallery of generators

For golden, silver, and bronze, we've prepared versions of the Stern–Brocot tree with generators depicted through the seventh level. The golden chart is nothing but an exact remake of the one Wilson created for his golden horograms; it was remade for stylistic consistency with the other two new ones here.

As for numbering convention, we are extending the numbering system used by David J. Finnamore on the Elven Minstrel site. His numbering system, as opposed to Wilson's, allows for further levels to be included without requiring renumbering. We extend the numbering system by prefixing numbers for generators for metallic means beyond golden with their metal number and an underscore; e.g. the eighth silver generator would be #2_8.

Each metal is also accompanied by a diagram of its patterns of generator equivalence, i.e. each generator has infinite different ways of being expressed as we travel deeper and deeper into the tree, but those infinite sequences of different ways follow patterns. In each of the boxes of these diagrams, the top half is a simple code that explains the type of equivalence:

1. P or C: Parent or Child. Does the interval lean toward the parent ratio or the child ratio?
2. L or G: Lesser or Greater: Does the interval run from the child ratio to its lesser parent or to its greater parent?
3. #: Isotope Number.

The bottom halves of each box are snippets of what such an equivalence looks like on the Scale Tree.

The Master Scale Table includes cents values for octave periods.

Golden

Golden metallic MOS scale table: for text values, to copy & paste

Generator equivalence patterns—golden

Silver

Silver metallic MOS scale table: for text values, to copy & paste

Generator equivalence patterns—silver

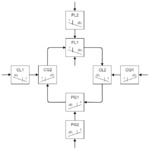
Bronze

Bronze metallic MOS scale table: for text values, to copy & paste

Generator equivalence patterns—bronze

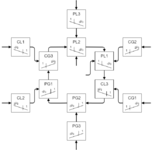
Beyond bronze

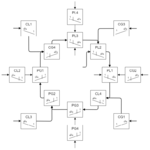
Including scale trees beyond bronze is outside the scope of this present work. However, an additional generator equivalence pattern diagram for the fourth metallic mean is illustrative of that meta-pattern as it continues to expand.

Generator equivalence patterns—4th metal

Master scale table

Master metallic MOS scale table

Well-known met-MOS scales

Golden Meantone

The thinking behind Golden Meantone is to put the whole step and half step into the ratio of φ with each other. Most discussion of Golden Meantone assumes a twelve-note scale that spans an octave.

Abstractly speaking, Golden Meantone's generator is a noble generator weighted by φ from 1/3 toward 1/2, [math]\approx 0.419821[/math], which by design was the one chosen for all noble generator examples in this discussion.

Wilson called this scale Kornerup, after Thorvald Kornerup, who was an early explorer of golden scales.

Wilson/Pepper Fifth Tuning

The thinking behind this tuning is similar, except that the two steps in the ratio of φ with each other are the tone and the chromatic semitone.

Abstractly speaking, Wilson/Pepper Fifth Tuning's generator would be the noble generator weighted by φ from 2/5 to 3/7, [math] \approx 0.413254[/math].

A tuning called Peppermint uses this fifth.

Non-Octave Golden

Golden lemba is a Multi-MOS, fitting two periods into an octave (600¢ period, 229.179¢ generator).

Golden triforce similarly fits three periods into an octave (400¢ period, 152.786¢ generator).

Argent Temperament

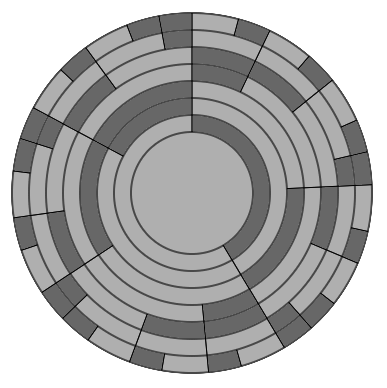
Scales based on the bronze mean and metallic means beyond it have not been extensively explored. However, the silver mean has gotten some attention.

Most discussion of Argent Temperament—like Golden Meantone—assumes an octave period; the thinking behind it is to put the fifth and the fourth into the ratio of [math]\sqrt{2}[/math] with each other. The justly tuned versions of these intervals, 3/2 and 4/3, respectively, are remarkably close to this already, only off by a fiftieth of a cent:

Interval name	Value	As portion of period	As cents
JI fifth	3/2	0.584963	701.96
Argent fifth	[math]2 - \sqrt{2}[/math]	0.585786	702.94
JI fourth	4/3	0.415037	498.04
Argent fourth	[math]\sqrt{2} - 1[/math]	0.414214	497.06

To know how to define this scale in terms of the present discussion, we recognize:

1. [math]\sqrt{2}[/math] is the first isotope of the silver mean, δ_s − 1.
2. The fifth and the fourth sum to the period, so we can use one or the other as the generator; we'll prefer the reduced one, the fourth.

So in our terms, this would be an isotopic generator, and again, by design, this was the isotopic generator chosen for examples in this discussion, approximately 0.414214.

It may seem odd that the most popular use of the silver mean uses its isotope rather than the mean directly. However, if we consider the ratio of the generator to the period here, that ratio is the silver mean. In the golden case, there was no difference between these two conceptions; both splitting the period into two segments in the ratio of φ and having the generator to period ratio be φ produce the same result. So while in this discussion from the beginning we put things in terms of splitting intervals (in order to smoothly transition from the golden generator into noble generators), it is probably the case that those who first brought us the Fibonacci generator and Argent Temperament were thinking in terms of the ratio of the generator to the period.

Argent means "silver" in French, which explains the name (it has also been called Arguros, which is "silver" in Greek). Wilson called this generator "2-Zig/2-Zag", after the pattern of the lines in the Stern–Brocot tree that results as we travel deeper into the tree searching for better approximations of it: we move twice to the right, then twice to the left, and repeat.

Imaginary

If Argent temperament splits the period into segments in the ratio of the silver ratio's isotope, what if we split the period into segments in the ratio of the silver mean itself? That gives us a generator of approximately 0.292893, which has been used by Billy Stiltner, who calls it Imaginary.

Twice 0.292893 is equal to 0.585786, which is the complement of Argent Temperament's generator, 0.414214. Despite this similarity, these two generate tremendously different scales (compare with the silver horogram shown earlier).

Other Wilson scales

Wilson gave names to a select few of the noble generators he described, and these have gotten some attention:

Name	Generator	Name explanation	Alternative names
Fibonacci	0.381966	Cardinality sequence is the Fibonacci numbers	Golden Father
Lucas	0.276393	Cardinality sequence is the Lucas numbers	—
Hanson	0.264308	Larry Hanson taught Wilson zigzag patterns.	—

Bonus topics

Split segment ratios

In the section about weighted mediants we observed that, when we split an interval in two by its weighted mediant, the ratio between these two segments is not equal to the weight. We may wonder what the ratio is between the two segments, then.

The two segments are actually in a ratio equal to the weight multiplied by the ratio of the denominators of their respective bounds.

We'll test this out on the example from before. We know that the weighted mediant formula with φ as weight, the interval between 1/3 and 1/2, and weight leaning toward the parent ratio 1/2 gives the value [math]\approx 0.419821[/math]. So our two segments are:

[math] s_1 = 0.419821 - 0.333333 = 0.086487 \\ s_2 = 0.500000 - 0.419821 = 0.080179 [/math]

Their ratio is

[math] r = \frac{s_1}{s_2} = \frac{0.086487}{0.080179} = 1.078674 [/math]

Which we can see is the weight multiplied by the bounding ratios' denominators:

[math] 1.078674 = \phi · \frac 23 [/math]

In particular, we see that the denominator of the weighted ratio finds itself on the same side of the ratio as the weight.

The full derivation follows. With lower bounding ratio [math]\frac{a_1}{a_2}[/math] and upper bounding ratio [math]\frac{b_1}{b_2}[/math], we have a mediant of [math]\frac{\phi a_1 + b_1}{\phi a_2 + b_2}[/math]. So then the segment from the lower bounding ratio to the mediant has length

[math] \require{cancel} \begin{align} s_1 &= \frac{\phi a_1 + b_1}{\phi a_2 + b_2} - \frac{a_1}{a_2} \\ &= \frac{a_2(\phi a_1 + b_1)}{a_2(\phi a_2 + b_2)} - \frac{a_1(\phi a_2 + b_2)}{a_2(\phi a_2 + b_2)} \\ &= \frac{a_2(\phi a_1 + b_1) - a_1(\phi a_2 + b_2)}{a_2(\phi a_2 + b_2)} \\ &= \frac{\phi a_1a_2 + a_2b_1 - \phi a_1a_2 - a_1b_2}{\phi a_2^2 + a_2b_2} \\ &= \frac{\cancel{\phi a_1a_2} + a_2b_1 - \cancel{\phi a_1a_2} - a_1b_2}{\phi a_2^2 + a_2b_2} \\ &= \frac{a_2b_1 - a_1b_2}{\phi a_2^2 + a_2b_2} \end{align} [/math]

and the segment from the mediant to the upper bounding ratio has length

[math] \require{cancel} \begin{align} s_2 &= \frac{b_1}{b_2} - \frac{\phi a_1 + b_1}{\phi a_2 + b_2} \\ &= \frac{b_1(\phi a_2 + b_2)}{b_2(\phi a_2 + b_2)} - \frac{b_2(\phi a_1 + b_1)}{b_2(\phi a_2 + b_2)} \\ &= \frac{b_1(\phi a_2 + b_2) - b_2(\phi a_1 + b_1)}{b_2(\phi a_2 + b_2)} \\ &= \frac{\phi a_2b_1 + b_1b_2 - \phi a_1b_2 - b_1b_2}{\phi a_2b_2 + b_2^2} \\ &= \frac{\phi a_2b_1 + \cancel{b_1b_2} - \phi a_1b_2 - \cancel{b_1b_2}}{\phi a_2b_2 + b_2^2} \\ &= \frac{\phi a_2b_1 - \phi a_1b_2}{\phi a_2b_2 + b_2^2} \end{align} [/math]

so then their ratio is

[math] \require{cancel} \begin{align} r &= \frac{( \phi a_2b_1 - \phi a_1b_2 )(\phi a_2^2 + a_2b_2)}{(\phi a_2b_2 + b_2^2)( a_2b_1 - a_1b_2 )} \\ &= \frac{\phi( a_2b_1 - a_1b_2 )a_2(\phi a_2 + b_2)}{b_2(\phi a_2 + b_2)( a_2b_1 - a_1b_2 )} \\ &= \frac{\phi\cancel{( a_2b_1 - a_1b_2 )}a_2\cancel{(\phi a_2 + b_2)}}{b_2\cancel{(\phi a_2 + b_2)}\cancel{( a_2b_1 - a_1b_2 )}} \\ &= \frac{\phi a_2}{b_2} \end{align} [/math]

The fact that the numerators do not figure into the result at all speaks to the impossibility of finding more than one interval on the tree with the same two bounding ratio denominators.

We can also infer why the ratio worked out to exactly φ in the case of the entire period: both of the denominators of 0/1 and 1/1 are 1, so the scalar on φ was 1.

And from this we also ascertain that weighted mediants sometimes fall toward the edges of the interval and sometimes toward the middle. I.e. if we choose the interval 8/21 to 5/13, weighted by φ toward 5/13, the ratio between the two split segments would be 8/21 ≈ 1.001640, making that split almost right down the middle; on the other hand, if we chose the interval 0/1 to 1/7, weighted by φ toward 1/7, the ratio between the two split segments would be 7φ ≈ 11.326238, extremely off.

Generator introduction counts

Each new level of the Stern–Brocot tree introduces the next power of 2 more intervals, but this does not necessarily mean the next power of 2 more generators. Many potential new generators are equivalent to ones which have already been found in shallower levels. Some interesting patterns arise in the counts of truly new generators introduced per level. They are similar but different from one metallic mean to the next:

Level	Golden mean	Silver mean or isotope	Bronze mean or isotope	4th Metallic mean or isotope
1	1	1	1	1
2	1*	2	2	2
3	2	3*	4	4
4	4	6	7*	8
5	8	12	14	15*
6	16	24	28	30
7	32	48	56	60

Each metal has one asterisked row. This row is the one where the pattern of increasing twofold gets temporarily impacted by a single subtraction of 1; thenceforth, twofold growth continues.

To be clear, this chart is indicating that if we only considered, e.g., the silver mean's isotope, then by level 1 we'd have 1 total generator, by level 2 we'd have 3, by level 3 we'd have 6, by level 4 we'd have 12, and then by levels 5, 6, and 7 we'd have 24, 48, and 96, respectively.

But we don't find generators for specific means or isotopes in isolation of their other isotopes; it is more helpful to consider the pattern of counts of new generator introductions for the entire family of values for each metal:

Level	Golden mean	Silver mean or isotope	Bronze mean or isotope	4th Metallic mean or isotope
1	1	2	3	4
2	1	2	3	4
3	2	4	6	8
4	4	8	12	16
5	8	16	24	32
6	16	32	48	64
7	32	64	96	128

And here we can see the pattern is even simpler. For gold it is the same, because it has no relevant isotopes. And the other metals simply map their metallic number over the values that gold finds.

So by the 7th level, when looking at the bronze scale tree, we should see a total of

[math] 3+3+6+12+24+48+96 = 192 [/math]

different generators.

-ishes

Some of the metallic means have special connections to each other. For example, the fourth metallic mean can be expressed in terms of the golden mean in a couple different ways:

[math]\qquad {}_{4}\mu_{4} \approx 4.236067978 = 2\phi + 1 = \phi^3 [/math]

The eleventh metallic mean, too, can be expressed in terms of the golden mean:

[math]\qquad {}_{11}\mu_{11} \approx 11.0901699437 = 5\phi + 3 = \phi^5 [/math]

In fact, every odd power of φ will be equivalent to a higher metallic mean. Whichever metallic mean that is will be the sum of two Fibonacci numbers F_n and F_{n − 2} (e.g. 4 = 3 + 1, and 11 = 8 + 3). For the alternative expression of the higher metallic mean as a constant plus some coefficient on the golden mean, the values of the constant and the coefficient will also be values from the Fibonacci series (e.g. 1 & 2, 3 & 5).

We suggest referring to these particular metallic means as goldenish means.

The connections between these metallic means are explained by their ratio forms. All goldenish means can be expressed in the form:

[math]\qquad \frac{m + n\sqrt5}{2} [/math]

For the golden mean, m = 1 and n = 1; for the fourth metallic mean, m = 4 and n = 2.

If we use [math]\phi^2[/math] as our generator (note: not as a logarithmic generator, but as an acoustic one, i.e. we repeat the generator by multiplying it, not adding it), then all of the pitches in our scale will be goldenish means (relatively speaking; if we multiplied every one by φ, preserving their ratios, they would be). Equivalently, we could include goldenish means until we found scales with exactly two step sizes, then divide every pitch by their shared factor of φ.

In another fun bit of synergy, moments of symmetry for this generator will be found at cardinalities from the Fibonacci series. That is, this generator produces scales with cardinality sequences of 2, 3, 5, 8, 13, 21 ...

The same principles hold for every other metallic mean. For instance, the second silverish mean is the 14th metallic mean:

[math]\qquad {}_{14}\mu_{14} \approx 14.07106781 = 5\delta_s + 2 = \delta_s^3 [/math]

and the third silverish mean is the 82nd metallic mean:

[math]\qquad {}_{82}\mu_{82} \approx 82.0121932454 = 29\delta_s + 12 = \delta_s^5 [/math]

The silverish means can also all be expressed in a ratio form, but where the golden mean uses [math]\sqrt5[/math], they use [math]\sqrt2[/math].

The pattern of powers remains the same for any metallic mean's -ishes: they are the odd powers. However, while the goldenish means draw their coefficients, constants, and cardinalities from the Fibonacci numbers, the silverish means draw theirs from their equivalent recurrence relation, the Pell numbers (2, 5, 12, 29, 70 ... )

So, if we use δ_s² as our generator, then we get silverish scales, whose pitches are all silverish means.

And if we use δ_b² as our generator, we can generate bronzish scales.

Further reading

Other metallic xenharmonic but not met-MOS

• Bohlen's 833 cent scale: Acoustic phi features prominently in this scale, giving rise to recursive stacks of combination tones.
• Brinko: Also see this.
• Metallic Harmonic Series
• Merciful intonation
• Regions of the Interval Spectrum - Some Concepts and Names

Other met-MOS

• Golden Ratio on the Xen Wiki: Contains a bunch of interesting links.
• Elven Minstrel: A fun and helpful take on noble MOS scales.
• Logarithmic Approximants: This article covers some fascinating ideas, and toward the end touches upon Golden Meantone and Argent Temperament, with thought-provoking visualizations.
• another Wilson document: This document includes 2-Zig/2-Zag.
• Sevish's phi scale: Synthesizes acoustic and logarithmic phi.
• Musical Patterns - MetMOS: Author's site. Contains a rudimentary interactive MetMOS generator.

Other MOS

• MOS generator: Helpful tool for generating horograms and quickly finding cardinality sequences.

Continued fractions

• Discussion about Continued fractions: Very detailed.
• Continued Fraction Calculator: An indispensable tool for calculating continued fractions, from the same source.

Stern–Brocot tree

• Farey sequence: Another way of slicing and dicing the texture of rationals.

Metallic means

• The Family of Metallic Means: Generalizes patterns of the metallic means even beyond the ones used in this discussion.
• rabbit sequences: Follow the same pattern as the horogram for the golden generator.
• Numberphile's playlist of videos related to the Golden Ratio: Some fun and informative videos on metallic means.

Glossary

• Cycle, interval pattern: The periodic part at the end of an interval pattern sequence.
• Cycle, L:s: The periodic part at the end of an sequence, cycling through the isotopes of the given metallic mean.
• Generator, aristocratic: A generator which is found using the weighted mediant formula on a non-period Stern–Brocot tree interval with a beyond golden mean.
• Generator, bronze: The generator found using the weighted mediant formula on the period interval with the golden mean, equal to [0; 4, 3] ≈ 0.232408.
• Generator, complement: A generator g's complement generator is equal to 1 − g.
• Generator, golden: The generator found using the weighted mediant formula on the period interval with the golden mean, equal to [0; 4, 3] ≈ 0.381966.
• Generator, isotopic: A generator found using the weighted mediant formula on the period interval with any isotope of a beyond golden mean.
• Generator, isotopic aristocratic: A generator found using the weighted mediant formula on a non-period Stern–Brocot tree interval with any isotope of a beyond golden mean.
• Generator, metallic: A generator found using the weighted mediant formula on any interval from the Stern–Brocot tree (including the period interval) with any metallic mean or isotope.
• Generator, noble: A generator which is found using the weighted mediant formula on a non-period Stern–Brocot tree interval with the golden mean.
• Generator, reduced: Of the generator and its complement, the lesser of the two; the one less than 0.5.
• Generator, silver: The generator found using the weighted mediant formula on the period interval with the silver mean, equal to [0; 3, 2] ≈ 0.292893.
• Interval pattern: A recursive interval relationship pattern exhibited by met-MOS scales.
• Level: A measure of depth in the Stern–Brocot tree, with the root being 1.
• Lean: Of a generator, its weighted mediant formula used to find it, which of two bounding ratios received the weight: the parent ratio, or the child ratio.
• Lean, parentward: The weighted mediant formula received the weight on the parent ratio.
• Lean, childward: The weighted mediant formula received the weight on the child ratio.
• Sequence, cardinality: For a given scale sequence, the corresponding sequence of their cardinalities.
• Sequence, interval pattern: For a given scale sequence, the corresponding sequence of their interval patterns.
• Sequence, L:s: For a given scale sequence, the corresponding sequence of their ratios.
• Sequence, scale: The ordered sequence of scales a generator generates, each one containing the previous, strictly adding new pitches to it.