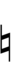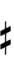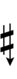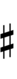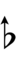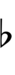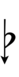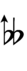13edo
| ← 12edo | 13edo | 14edo → |
13 equal divisions of the octave (abbreviated 13edo or 13ed2), also called 13-tone equal temperament (13tet) or 13 equal temperament (13et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 13 equal parts of about 92.3 ¢ each. Each step represents a frequency ratio of 21/13, or the 13th root of 2.
Theory
13edo has a sharp fifth of 738c, which serves sort of an opposite role to 9edo's flat fifth of 667 cents (in fact, they are both separated from 3/2 by approximately the same amount in opposite directions). Notably for scale theory, this sharp fifth is extremely close to the golden generator of 741 cents, and so 13edo has the MOS scales 2L 1s, 3L 2s, and 5L 3s and functions as an equalized 8L 5s.
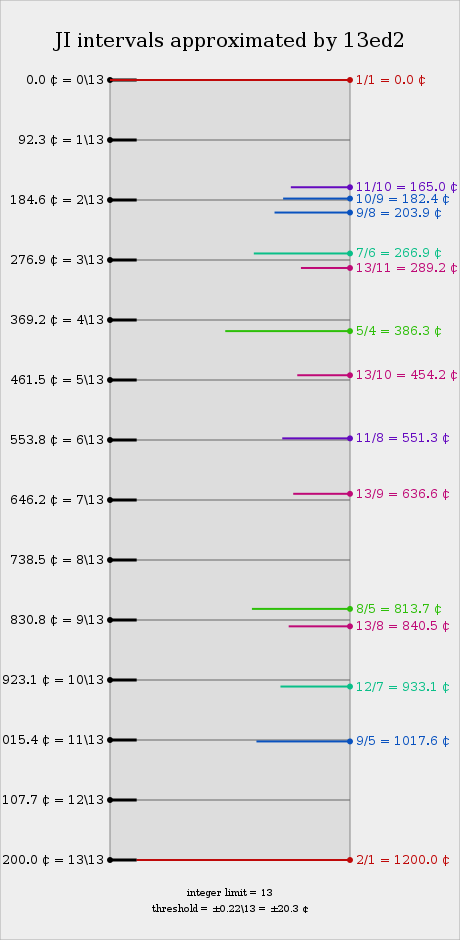
The simplest JI interpretation of 13edo is in the 2.5.11 subgroup, in which it approximates intervals such as 11/10, 121/80, and 64/55. However, it notably has very good approximations to 13, 17, and 19 as well.
Additionally, 13edo has an excellent approximation to the 21st harmonic, and a reasonable approximation to the 9th harmonic. For most purposes it does not offer acceptable approximations to the 3rd, 7th, or 15th. The lack of reasonable approximation to the 3rd harmonic makes 13edo unsuitable for common-practice music, but its good approximations to ratios of 11, 13, and 21 make it a very xenharmonic tuning, as these identities are not remotely represented in 12edo. Despite its reputation for dissonance, it is an excellent rank-1 subgroup temperament, with the 2.5.9.11.13.17.19.21 subgroup being a particularly good example. It has a substantial repertoire of complex consonances for its small size.
One step of 13edo is very close to 135/128 by direct approximation (it is a semiconvergent).
In 13edo, the steps less than 600¢ are narrower than their nearest 12edo approximation, while those greater than 600¢ are wider. This allows for some neat ear-bending tricks, whereby melodic gestures reminiscent of 12edo can quickly arrive at an unfamiliar place.
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +36.5 | -17.1 | -45.7 | -19.3 | +2.5 | -9.8 | +19.4 | -12.6 | -20.6 | -9.2 | +17.9 |
| Relative (%) | +39.5 | -18.5 | -49.6 | -20.9 | +2.7 | -10.6 | +21.0 | -13.7 | -22.3 | -10.0 | +19.4 | |
| Steps (reduced) |
21 (8) |
30 (4) |
36 (10) |
41 (2) |
45 (6) |
48 (9) |
51 (12) |
53 (1) |
55 (3) |
57 (5) |
59 (7) | |
Subsets and supersets
13edo is the sixth prime edo, following 11edo and coming before 17edo.
The 5-limit aluminium temperament (supported by 65edo, 494edo and 1547edo) realizes this proximity through a regular temperament perspective, combining the sound of 13edo with the simplicity of 5-limit JI. (See regular temperament for more about what this means and how to use it.) A notable smaller superset is 26edo, which is a good flattone tuning, although its step has very high harmonic entropy. An intermediate-sized superset is 39edo, which corrects the 3rd and (marginally) 5th harmonics better (but is worse for the 7th harmonic) and has a step size with less harmonic entropy than 26edo, while having a more manageable number of notes than 65edo.
Intervals
13edo chromatic ascending and descending scale on C (MIDI)
| # | Cents | Approximated 21-odd-limit Ratios[1] | Erv Wilson | Archaeotonic
(Heptatonic 2nd-generated) |
Oneirotonic
(Octatonic 5th-generated) |
26edo names
(subset notation) |
Fox-Raven (J = 360Hz) |
Pseudo-Diatonic Category |
Audio |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00 | 1/1 | H | C | C | C | J | Unison | |
| 1 | 92.31 | 17/16, 18/17, 19/18, 20/19, 21/20, 22/21 | β | C#/Db | C#/Db | Cx/Dbb | J#/Kb | Minor second | |
| 2 | 184.62 | 9/8, 10/9, 11/10, 19/17, 21/19 | A | D | D | D | K | Major second | |
| 3 | 276.92 | 7/6, 13/11, 20/17, 19/16, 22/19 | δ | D#/Eb | D#/Eb | Dx/Ebb | L | Minor third | |
| 4 | 369.23 | 5/4, 11/9, 16/13, 26/21 | C | E | E | E | L#/Mb | Major third | |
| 5 | 461.54 | 13/10, 17/13, 21/16, 22/17 | B | E#/Fb | F | Ex/Fb | M | Minor fourth | |
| 6 | 553.85 | 11/8, 18/13, 26/19 | ε | F | F#/Gb | F# | M#/Nb | Major fourth/Minor tritone | |
| 7 | 646.15 | 16/11, 13/9, 19/13 | D | F#/Gb | G | Gb | N | Minor fifth/Major tritone | |
| 8 | 738.46 | 17/11, 20/13, 26/17, 32/21 | γ | G | G#/Hb | G# | O | Major fifth | |
| 9 | 830.77 | 8/5, 13/8, 18/11, 21/13 | F | G#/Ab | H | Ab | O#/Pb | Minor sixth | |
| 10 | 923.08 | 17/10, 12/7, 22/13, 19/11 | E | A | A | A# | P | Major sixth | |
| 11 | 1015.38 | 9/5, 16/9, 20/11, 34/19, 38/21 | α | A#/Bb | A#/Bb | Bb | Q | Minor seventh | |
| 12 | 1107.69 | 17/9, 19/10, 21/11, 32/17, 36/19, 40/21 | G | B/Cb | B | B#/Cbb | Q#/Jb | Major seventh | |
| 13 | 1200.00 | 2/1 | H | C/B# | C | C | J | Octave |
- ↑ Ratios are based on treating 13edo as a 2.5.9.11.13.21 subgroup temperament; other approaches are possible.
Notations
There are seven categories of notation. Only the first two categories are backwards-compatible. They both allow conventional notation to be used, including the staff, note names, relative notation, chord names, etc. And they both allow a piece in conventional notation to be translated to 13edo. They both use the conventional genchain of fifths:
...Db - Ab - Eb - Bb - F - C - G - D -A - E - B - F#- C# - G# - D#...
...d8 - d5 - m2 - m6 - m3 - m7 - P4 - P1 - P5 - M2 - M6 - M3 - M7 - A4 - A1...
Except the first version of the second notation swaps sharp and flat, major and minor, and augmented and diminished.
Heptatonic 5th-generated (wide 5th)
13edo can also be notated with ups and downs. If one uses the best fifth, 8\13, the minor 2nd becomes a descending interval! Thus a major 2nd is wider than a minor 3rd, a major 3rd is wider than a perfect 4th, etc. And B is above C, E is above F, A is above Bb, etc. However one can use ups and downs to avoid minor 2nds. Thus A C B D becomes A vB ^C D.
Enharmonic unisons: v⁴A1, ^m2
| # | Cents | Up/down notation using the wide 5th of 8\13 | ||
|---|---|---|---|---|
| 0 | 0 | perfect unison | P1 | D |
| 1 | 92 | up unison, mid 2nd | ^1, ~2 | ^D, ^^Eb, vvE |
| 2 | 185 | downmajor 2nd, (minor 3rd) | vM2, (m3) | vE, (F) |
| 3 | 277 | major 2nd, upminor 3rd | M2, ^m3 | E, ^F |
| 4 | 369 | mid 3rd | ~3 | ^^F, vvF# |
| 5 | 462 | perfect 4th | P4 | G |
| 6 | 554 | up 4th, dud 5th | ^4, vv5 | ^G, vvA |
| 7 | 646 | dup 4th, down 5th | ^^4, v5 | ^^G, vA |
| 8 | 738 | perfect 5th | P5 | A |
| 9 | 831 | mid 6th | ~6 | ^^Bb, vvB |
| 10 | 923 | downmajor 6th, minor 7th | vM6 | vB, C |
| 11 | 1015 | (major 6th), upminor 7th | (M6), ^M7 | (B), ^C |
| 12 | 1108 | mid 7th, down 8ve | ~7, v8 | ^^C, vvC#, vD |
| 13 | 1200 | perfect 8ve | P8 | D |
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
|
| ||
| Flat symbol | |
|
|
|
|
|
Half-sharps and half-flats can also be used, making the ascending scale:
D E ![]() vE ^F F
vE ^F F ![]() G ^G vA A B
G ^G vA A B ![]() vB ^C C
vB ^C C ![]() D
D
Heptatonic 5th-generated (narrow fifth)
The notational 5th is the 2nd-best approximation of 3/2, 7\13. This is 56¢ flat of 3/2, and the best approximation is 36¢ sharp, noticeably better. But using the 2nd-best 5th avoids the minor 2nd being descending.
There are two ways to do this. The first way preserves the melodic meaning of sharp/flat, major/minor and aug/dim, in that sharp is higher pitched than flat, and major/aug is wider than minor/dim. The disadvantage to this approach is that conventional interval arithmetic no longer works. e.g. M2 + M2 isn't M3, and D + M2 isn't E. Chord names are different because C - E - G isn't P1 - M3 - P5.
The second approach preserves the harmonic meaning of sharp/flat, major/minor and aug/dim, in that the former is always further fifthwards on the chain of fifths than the latter. Sharp is lower in pitch than flat, and major/aug is narrower than minor/dim. While this approach may seem bizarre at first, interval arithmetic and chord names work as usual. Furthermore, conventional 12edo music can be directly translated to 13edo "on the fly".
The first approach has Enharmonic unisons of a trud-augmented 1sn and a downminor 2nd. The second approach has a trup-augmented 1sn and a downmajor 2nd.
| # | Cents | Up/down notation using the narrow 5th of 7\13, with major wider than minor |
Up/down notation using the narrow 5th of 7\13, with major narrower than minor | ||||
|---|---|---|---|---|---|---|---|
| 0 | 0 | perfect unison | P1 | D | perfect unison | P1 | D |
| 1 | 92 | up unison, minor 2nd | ^1, m2 | ^D, E | up unison, major 2nd | ^1, M2 | ^D, E |
| 2 | 185 | upminor 2nd, minor 3rd | ^m2, m3 | ^E, Fb | upmajor 2nd, major 3rd | ^M2, M3 | ^E, F# |
| 3 | 277 | downmajor 2nd, upminor 3rd | vM2, ^m3 | vE#, ^Fb | downminor 2nd, upmajor 3rd | vm2, ^M3 | vEb, ^F# |
| 4 | 369 | major 2nd, downmajor 3rd | M2, vM3 | E#, vF | minor 2nd, downminor 3rd | m2, vm3 | Eb, vF |
| 5 | 462 | major 3rd, down 4th | M3, v4 | F, vG | minor 3rd, down 4th | m3, v4 | F, vG |
| 6 | 554 | perfect 4th, down 5th | P4, v5 | G, vA | perfect 4th, down 5th | P4, v5 | G, vA |
| 7 | 646 | up 4th, perfect 5th | ^4, P5 | ^G, A | up 4th, perfect 5th | ^4, P5 | ^G, A |
| 8 | 738 | up 5th, minor 6th | ^5, m6 | ^A, B | up 5th, major 6th | ^5, M6 | ^A, B |
| 9 | 831 | upminor 6th, minor 7th | ^m6, m7 | ^B, Cb | upmajor 6th, major 7th | ^M6, M7 | ^B, C# |
| 10 | 923 | downmajor 6th, upminor 7th | vM6, ^m7 | vB#, ^Cb | downminor 6th, upmajor 7th | vm6, ^M7 | vBb, ^C# |
| 11 | 1015 | major 6th, downmajor 7th | M6, vM7 | B#, vC | minor 6th, downminor 7th | m6, vm7 | Bb, vC |
| 12 | 1108 | major 7th, down 8ve | M7, v8 | C, vD | minor 7th, down 8ve | m7, v8 | C, vD |
| 13 | 1200 | perfect 8ve | P8 | D | perfect 8ve | P8 | D |
Pentatonic 5th-generated (3L2s)
The degrees are named unison, subthird, fourthoid, fifthoid, subseventh and octoid.
Keyboard: D * F * * G * * A * C * * D (generator = wide 3/2 = 8\13 = perfect 5thoid)
Enharmonic unison: dds3
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | D#
Fb |
F | F# | Gb | G | G# | Ab | A | A#
Cb |
C | C# | Db | D |
| P1 | A1
ds3 |
ms3 | Ms3 | As3
d4d |
P4d | A4d | d5d | P5d | A5d
ds7 |
ms7 | Ms7 | As7
d8d |
P8d |
| ... | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ... | Fb | Cb | Gb | Db | Ab | F | C | G | D | A | F# | C# | G# | D# | A# | Fx | Cx | ... |
| ... | ds3 | ds7 | d4d | d8d | d5d | ms3 | ms7 | P4d | P1 | P5d | Ms3 | Ms7 | A4d | A1 | A5d | As3 | As7 | ... |
Octatonic 5th-generated (5L3s or oneirotonic)
Keyboard: A * B C * D * E F * G H * A (generator = wide 3/2 = 8\13 = perfect 6th)
Enharmonic unison: d2
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | A#
Bb |
B | C | C#
Db |
D | D#
Eb |
E | F | F#
Gb |
G | H | H#
Ab |
A |
| P1 | A1
m2 |
M2 | m3 | M3 | P4 | m5 | M5 | P6 | m7 | M7 | m8 | M8
d9 |
P9 |
| ... | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ... | D# | A# | F# | C# | H# | E | B | G | D | A | F | C | H | Eb | Bb | Gb | Db | ... |
| ... | A1 | A6 | M3 | M8 | M5 | M2 | M7 | P4 | P1 | P6 | m3 | m8 | m5 | m2 | m7 | d4 | d8 | ... |
Heptatonic 2nd-generated (6L1s or archaeotonic)
Keyboard: D * E * F * G A * B * C * D (generator = 2\13 = perfect 2nd)
Enharmonic unison: dd2
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | D#
Eb |
E | E#
Fb |
F | F#
Gb |
G | A | A#
Bb |
B | B#
Cb |
C | C#
Db |
D |
| P1 | A1
d2 |
P2 | m3 | M3 | m4 | M4 | m5 | M5 | m6 | M6 | P7 | A7
d8 |
P8 |
| ... | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ... | Db | Eb | Fb | Gb | A | B | C | D | E | F | G | A# | B# | C# | D# | ... |
| ... | d8 | d2 | m3 | m4 | m5 | m6 | P7 | P1 | P2 | M3 | M4 | M5 | M6 | A7 | A1 | ... |
Heptatonic 3rd-generated (3L4s or mosh)
This notation requires ups and downs because 7 perfect thirds octave-reduces to 2 edosteps, not 1.
Keyboard: D E * * F G * * A B * * C D (generator = 4\13 = perfect 3rd)
Enharmonic unisons: vvA1, vm2
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | E | ^E
Fb |
E#
vF |
F | G | ^G
Ab |
G#
vA |
A | B | ^B
Cb |
B#
vC |
C | D |
| P1 | m2 | ~2
d3 |
M2
v3 |
P3 | m4 | ~4
m5 |
M4
~5 |
M5 | P6 | ^6
m7 |
A6
~7 |
M7 | P8 |
| ... | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ... | Db | Fb | Ab | Cb | E | G | B | D | F | A | C | E# | G# | B# | D# | ... |
| ... | d8 | d3 | m5 | m7 | m2 | m4 | P6 | P1 | P3 | M5 | M7 | M2 | M4 | A6 | A1 | ... |
26edo subset
This notation uses every other note name of 26edo. There are no perfect 4ths or 5ths, only augmented and diminished ones. There are no minor 2nds or augmented 1sns.
There are two versions of the absolute notation. One has only three natural notes (C, D and E) and the other one has only four (F, G, A and B).
Keyboard: D * E * * * * * * * * C * D or * * * F * G * A * B * * * * (generator = 4\26 = 2\13 = major 2nd)
Enharmonic unison: ddd2
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| version #1 | D | Dx
Ebb |
E | Fb | F# | Gb | G# | Ab | A# | Bb | B# | C | Cx
Dbb |
D |
| version #2 | D# | Eb | E# | F | Fx
Gbb |
G | Gx
Abb |
A | Ax
Bbb |
B | Cb | C# | Db | D# |
| P1 | d2 | M2 | d3 | M3 | d4 | A4 | d5 | A5 | m6 | A6 | m7 | A7 | P8 |
| ... | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ... | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| version #1 | ... | Dbb | Ebb | Fb | Gb | Ab | Bb | C | D | E | F# | G# | A# | B# | Cx | Dx | ... |
| version #2 | ... | Gbb | Abb | Bbb | Cb | Db | Eb | F | G | A | B | C# | D# | E# | Fx | Gx | ... |
| ... | dd8 | d2 | d3 | d4 | d5 | m6 | m7 | P1 | M2 | M3 | A4 | A5 | A6 | A7 | AA1 | ... |
Sagittal notation
This notation is a subset of the notations for EDOs 26 and 52.
Evo flavor

Because it includes no Sagittal symbols, this Evo Sagittal notation is also a conventional notation.
Revo flavor

Approximation to JI
Selected 13-odd-limit intervals
Local zeta peak
At the local zeta peak of 13edo, there is an improvement in both acoustic phi and logarithmic phi.
Tuning by ear
13edo can be approximated by a circle of 64/49 subminor fourths (which can be tuned by tuning two 7/4 subminor sevenths). A stack of 13 of these subfourths closes with an error of +10.526432¢, or +11% of 13-edo's step size.
Approximation to irrational intervals
Golden ratio
13edo has a very good approximation of acoustic phi (9\13), with only -2.3 cents of error. The next better approximations are in 23edo and 36edo. As a coincidence, 13edo also has a very close appoximation of logarithmic phi (21\13), with only -3.2 cents of error. Logarithmic phi has some interesting applications in Metallic MOS.
Not until 144 do we find a better edo in terms of relative error on both of these two intervals.
See also: 9edϕ
| Interval | Error (abs, ¢) |
|---|---|
| 2ϕ / ϕ | 0.858 |
| ϕ | 2.321 |
| 2ϕ | 3.179 |
Scales
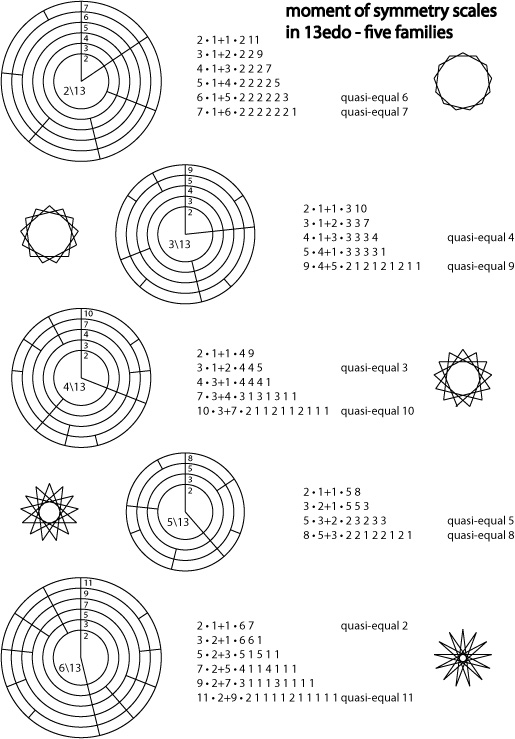
Important mosses (values in parentheses are (period, generator)):
- oneirotonic 5L 3s 22122121 (5\13, 1\1)
- archaeotonic 6L 1s 2222221 (2\13, 1\1)
- lovecraft 4L 5s 212121211 (3\13, 1\1)
- Sephiroth 3L 4s 3131311 (4\13, 1\1)
Due to the prime character of the number 13, 13edo can form several xenharmonic moment of symmetry scales. The diagram below shows five "families" of MOS scales: those generated by making a chain of 2\13 (two degrees of 13edo), 3\13, 4\13, 5\13, & 6\13, respectively.
~diagram by Andrew Heathwaite, based on horagrams pioneered by Erv Wilson
Another neat facet of 13edo is the fact that any 12edo scale can be "turned into" a 13edo scale by either adding an extra semitone, or turning an existent semitone into a whole-tone. Because of this, melody in 13edo can be quite mind-bending and uncanny, and phrases that begin in a familiar way quickly lead to something totally unexpected.
Harmony in 13edo
Contrary to popular belief, consonant harmony is possible in 13edo, but it requires a radically different approach than that used in 12edo (or other Pythagorean or Meantone-based tunings). Trying to approximate the usual major and minor triads of 12edo within 13edo is usually a disappointment if consonance is the goal; 0-3-7, 0-4-7, 0-3-8, and 0-4-8 are all rather rough in 13edo. Typically, the most consonant harmonies do not use a "stack of 3rds" the way they do in 12edo, since the strongest dissonances in 13edo are near the middle of the octave (degrees 6, 7, and 8). Instead, a stack of whole-tones, or a mixture of whole-tones and minor 3rds, often yields good results. For example, one way to view 13edo is as a subgroup temperament of harmonics 2.5.9.11.13. It actually performs quite admirably in this regard, and a chord of 0-4-15-19-22 (approximating 4:5:9:11:13) sounds very convincing. An even larger subgroup is the 2*13 subgroup 2.9.5.21.11.13, on which 13 has the same tuning and commas as 26edo.
By this, we can assume that the major ninth of 13edo can be thought of as analogous to the perfect fifth in 12edo and other meantone edos. This means that the major second or major ninth is the most consonant interval next to 2/1 in 13edo followed by 11/8, 5/4 and so on. The 4:5:9 chord can therefore be thought of as a possible basic harmonic triad in 13edo.
The 2.9.5.11.13 subgroup has commas 45/44, 65/64 and 81/80, leading to a linear temperament with POTE generator 185.728 cents, quite close to 2\13. Use this as a generator, and at 7 notes (6L 1s) two full pentads are available (as well as two more 4:5:9:11 tetrad, and one 4:5:9:13 tetrad). These triads and tetrads are likely the most consonant base sonorities available in 13edo and act in a similar way to major/minor triads. However, other sonorities such as Orwell chords are available as well.
Other approaches explored by specific composers and theorists are outlined further down, in the context of more complete tonal systems.
Play the 4:5:9 chord:
Play the 4:5:9:11 chord:
Play the 4:5:9:13 chord:
Play the 4:5:9:21 chord:
Notational and compositional approaches
13edo has drawn the attention of numerous composers and theorists, some of whom have devoted some effort to provide a notation and an outline of a compositional approach to it. Some of these are described below.
The Cryptic Ruse Methods
13edo offers two main candidates for diatonic-like scales: the 6L 1s heptatonic MOS generated by 2\13, and the 5L 3s octatonic MOS. Both of these scales are Rothenberg proper, and bear a slightly-twisted resemblance to the 12edo diatonic scale. Specifically, the 6L 1s scale resembles the 12edo diatonic with one of its semitones replaced with a whole-tone, while the 5L 3s scale resembles the 12edo diatonic with an extra semitone inserted between two adjacent whole-tones.
To facilitate discussion of these scales, Cryptic Ruse has ascribed them names based on H.P. Lovecraft's "Dream Cycle" mythos.
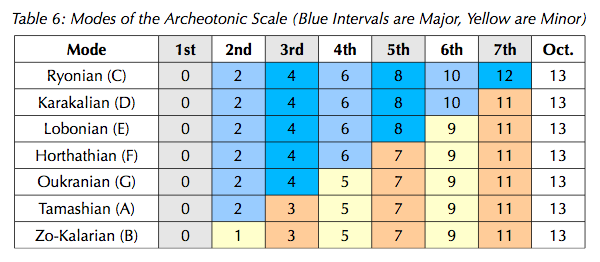
Modes and harmony in the archaeotonic scale
The 2\13-based heptatonic has been named archaeotonic after the "Old Ones" that rule the Dreamlands. Modes of the archaeotonic are named after the individual Old Ones.
A 7-nominal notation is proposed, using the letters A-G. The "C natural" scale is proposed to be degrees 0-2-4-6-8-10-12-(13), with the note "C" tuned to a reference pitch of concert middle C. The modes are laid out in the following table, excerpted from an unfinished paper on 13-edo.
Treating 13edo as a temperament as proposed above leads to a chord of degrees 0-2-4-6-9 representing the JI harmony 8:9:10:11:13; two such pentads exist in this scale, on E and F. Smaller harmonic units exist as follows: 8:9:10:11 on C, D, E, and F; 8:9:10:13 on E, F and G; 8:9:10 on C, D, E, F, and G; 8:9:11 on C, D, E, and F; 8:9:13 on E, F, G, and A. Finally, on B we have the relatively-discordant 16:17:21:26 (0-1-5-9, or the notes B-C-E-G), which can be octave-inverted into a more concordant 8:13:17:21.
There may be other concordant harmonies possible in this scale that do not represent segments of the harmonic series; further exploration is pending.
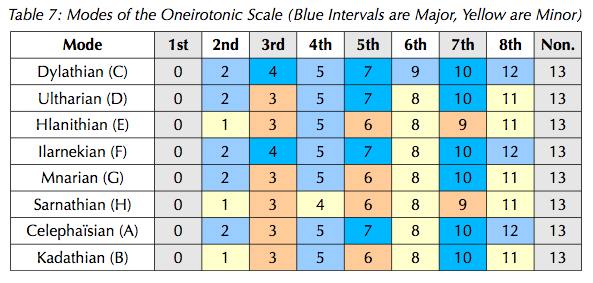
Modes and harmony in the oneirotonic scale
The 5\13-based octatonic has been named oneirotonic after the Dreamlands themselves. Modes of the oneirotonic are named after cities in the Dreamlands.
Here an 8-nominal notation is proposed, using letters A-H. The "C natural" scale is proposed to be degrees 0-2-4-5-7-9-10-12-(13), with the note "C" tuned to concert middle C. The modes are laid out in the following table, excerpted from an unfinished paper on 13edo.
There is a great number of potential consonant harmonies in this scale. A dedicated article on harmony and tonality in the oneirotonic scale is forthcoming.
Mapping to standard keyboards
The 5L+3s scale (Oneirotonic) can be mapped to the standard keyboard effectively, although somewhat awkwardly. Consider the sequence of 730-cent intervals that it derives from: 1 6 11 3 8 (13) 5 10 2 7 12 4 9 1/1. One of these must be absent, so it might as well be the last. So, there are at most five of the full octatonic scales on different keys. Of the four mappings that keep the major pentatonic on the white keys, which ironically look like ordinary minor-pentatonics, the latter which begins on B might be the most straightforward to learn and use.
| 1 | 6 | 11 | 3 | 8 | (13) | 5 | 10 | 2 | 7 | 12 | 4 | 9 | 1 | Place in Chain of 738.5 cent intervals |
| X | * | * | * | * | * | * | * | X | Marked are the octatonic scales (X=Sarnathian) | |||||
| * | * | * | * | X | * | * | * | |||||||
| * | X | * | * | * | * | * | * | |||||||
| * | * | * | * | * | * | X | * | |||||||
| * | * | * | X | * | * | * | * | |||||||
| D | Eb | E | F | Gb | G | Ab | A | Bb | B | C | Db | D | Keeps the pentatonic scale on the white keys | |
| A | Bb | B | C | Db | D | Eb | E | F | Gb | G | Ab | A | ||
| E | F | Gb | G | Ab | A | Bb | B | C | Db | D | Eb | E | ||
| B | C | Db | D | Eb | E | F | Gb | G | Ab | A | Bb | B | ||
| C | Db | D | Eb | E | F | Gb | G | Ab | A | Bb | B | C | Puts the missing key between a semitone | |
| G | Ab | A | Bb | B | C | Db | D | Eb | E | F | Gb | G | (if that were to be valuable in any way) |
The archaeotonic tonality is much simpler to deal with: you just leave out a tone and remember which one. Although, for diatonic use it may be more convenient to put the missing tone between E/F or B/C to keep it on the white keys, with the remaining small step where it looks like it should be.
Regular temperament properties
Uniform maps
| Min. size | Max. size | Wart notation | Map |
|---|---|---|---|
| 12.7050 | 12.8363 | 13beff | ⟨13 20 30 36 44 47] |
| 12.8363 | 12.8634 | 13be | ⟨13 20 30 36 44 48] |
| 12.8634 | 12.9341 | 13b | ⟨13 20 30 36 45 48] |
| 12.9341 | 13.0016 | 13 | ⟨13 21 30 36 45 48] |
| 13.0016 | 13.1066 | 13d | ⟨13 21 30 37 45 48] |
| 13.1066 | 13.1356 | 13df | ⟨13 21 30 37 45 49] |
| 13.1356 | 13.1524 | 13cdf | ⟨13 21 31 37 45 49] |
| 13.1524 | 13.3578 | 13cdeef | ⟨13 21 31 37 46 49] |
Commas
13et tempers out the following commas. (Note: This assumes the val ⟨13 21 30 36 45 48].)
| Prime limit |
Ratio[1] | Monzo | Cents | Color name | Name(s) |
|---|---|---|---|---|---|
| 5 | (14 digits) | [-21 3 7⟩ | 10.06 | Lasepyo | Semicomma, Fokker comma |
| 7 | 1029/1000 | [-3 1 -3 3⟩ | 49.49 | Trizogu | Keega |
| 7 | 525/512 | [-9 1 2 1⟩ | 43.41 | Lazoyoyo | Avicennma, Avicenna's enharmonic diesis |
| 7 | 64/63 | [6 -2 0 -1⟩ | 27.26 | Ru | Septimal comma, Archytas' comma, Leipziger Komma |
| 7 | 64827/64000 | [-9 3 -3 4⟩ | 22.23 | Laquadzo-atrigu | Squalentine comma |
| 7 | 3125/3087 | [0 -2 5 -3⟩ | 21.18 | Triru-aquinyo | Gariboh comma |
| 7 | 3136/3125 | [6 0 -5 2⟩ | 6.08 | Zozoquingu | Hemimean comma |
| 11 | 56/55 | [3 0 -1 1 -1⟩ | 31.19 | Luzogu | Undecimal diesis |
| 11 | 121/120 | [-3 -1 -1 0 2⟩ | 14.37 | Lologu | Biyatisma |
| 11 | 441/440 | [-3 2 -1 2 -1⟩ | 3.93 | Luzozogu | Werckisma |
| 13 | 40/39 | [3 -1 1 0 0 -1⟩ | 43.83 | Thuyo | Tridecimal minor diesis |
| 13 | 105/104 | [-3 1 1 1 0 -1⟩ | 16.57 | Thuzoyo | Animist comma |
| 13 | 169/168 | [-3 -1 0 -1 0 2⟩ | 10.27 | Thothoru | Buzurgisma |
- ↑ Ratios longer than 10 digits are presented by placeholders with informative hints
Animism
The animist comma, 105/104, appears whenever ~23 × ~13… 13edo does not approximate 3 and 7 individually (26edo does), but 13edo has 21/16 (21 = 3*7) and is also an animist temperament. In 13edo, the 5th harmonic is tuned so flatly that 5/4 = 16/13, leading to some interesting identities. So two scales stand out through this construction:
0 4 5 8 9 13 pentatonic
and
0 1 3 4 5 8 9 10 12 13 nonatonic
Introductory materials
By Inthar
- 13edo example composition (File:13edo 1MC score.pdf)
Oneirotonic Modal Studies
- : Tonal Study in Dylathian
- : Tonal Study in Ultharian
- : Tonal Study in Hlanithian
- : Tonal Study in Illarnekian
- : Tonal Study in Mnarian
- : Tonal Study in Sarnathian
- : Tonal Study in Celephaïsian
- : Tonal Study in Kadathian
Music
- See also: Category:13edo tracks
See also
- 13EDO Scales and Chords for Guitar
- Lumatone mapping for 13edo
- Well-Tempered 13-Tone Clavier (collab project to create 13edo keyboard pieces in a variety of keys and modes)
- Approaches:
- Fendo family - temperaments closely related to 13edo