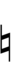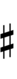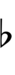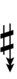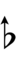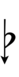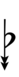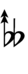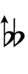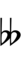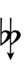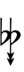32edo: Difference between revisions
→Delta-rational harmony: compression |
|||
| Line 1,255: | Line 1,255: | ||
| 0.00026 | | 0.00026 | ||
|} | |} | ||
== Octave stretch or compression == | |||
What follows is a comparison of compressed-octave 32edo tunings. | |||
; 32edo | |||
* Step size: 37.500{{c}}, octave size: 1200.0{{c}} | |||
Pure-octaves 32edo approximates all harmonics up to 16 within 15.5{{c}}. | |||
{{Harmonics in equal|32|2|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 32edo}} | |||
{{Harmonics in equal|32|2|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 32edo (continued)}} | |||
; [[WE|32et, 13-limit WE tuning]] | |||
* Step size: 37.481{{c}}, octave size: 1199.4{{c}} | |||
Compressing the octave of 32edo by around half a cent results in improved primes 3, 7 and 11, but worse primes 5 and 13. This approximates all harmonics up to 16 within 18.3{{c}}. Its 13-limit WE tuning and 13-limit [[TE]] tuning both do this. | |||
{{Harmonics in cet|37.481|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 32et, 13-limit WE tuning}} | |||
{{Harmonics in cet|37.481|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 32et, 13-limit WE tuning (continued)}} | |||
; [[WE|32et, 11-limit WE tuning]] | |||
* Step size: 37.453{{c}}, octave size: 1198.5{{c}} | |||
Compressing the octave of 32edo by around 1.5{{c}} results in improved primes 3, 7 and 11, but worse primes 2, 5 and 13. This approximates all harmonics up to 16 within 16.4{{c}}. Its 11-limit WE tuning and 11-limit [[TE]] tuning both do this. | |||
{{Harmonics in cet|37.453|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 32et, 11-limit WE tuning}} | |||
{{Harmonics in cet|37.453|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 32et, 11-limit WE tuning (continued)}} | |||
; [[ed7|90ed7]] | |||
* Step size: 37.431{{c}}, octave size: 1197.8{{c}} | |||
Compressing the octave of 32edo by around 2{{c}} results in improved primes 3, 7, 11 and 13, but worse primes 2 and 5. This approximates all harmonics up to 16 within 18.6{{c}}. If one wishes to use both of 32edo's mappings of the 5th harmonic simultaneously, this tuning is suited to that due to evenly sharing the error between them. The tuning 90ed7 does this. | |||
{{Harmonics in equal|90|7|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 90ed7}} | |||
{{Harmonics in equal|90|7|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 90ed7 (continued)}} | |||
; [[zpi|133zpi]] | |||
* Step size: 37.418{{c}}, octave size: 1197.375{{c}} | |||
Compressing the octave of 32edo by around NNN{{c}} results in improved primes 3, 7, 11 and 13, but worse primes 2 and 5. This approximates all harmonics up to 16 within 17.4{{c}}. The tuning 133zpi does this. | |||
{{Harmonics in cet|37.418|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 133zpi}} | |||
{{Harmonics in cet|37.418|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 133zpi (continued)}} | |||
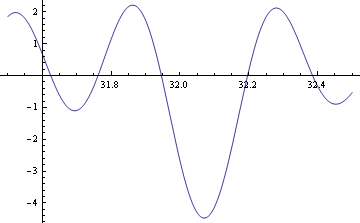
Below is a plot of the [[Zeta]] function, showing how its peak (ie biggest absolute value) is shifted above 32, corresponding to a zeta tuning with octaves flattened to 1197.375 cents. This will improve the fifth, at the expense of the third. | |||
[[File:plot32.png|alt=plot32.png|plot32.png]] | |||
; [[51edt]] | |||
* Step size: 37.293{{c}}, octave size: 1193.4{{c}} | |||
Compressing the octave of 32edo by around 6.5{{c}} results in improved primes 3, 5 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 18.2{{c}}. The tuning 51edt does this. | |||
{{Harmonics in equal|51|3|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 51edt}} | |||
{{Harmonics in equal|51|3|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 51edt (continued)}} | |||
== Instruments == | == Instruments == | ||
Latest revision as of 23:39, 29 August 2025
| ← 31edo | 32edo | 33edo → |
32 equal divisions of the octave (abbreviated 32edo or 32ed2), also called 32-tone equal temperament (32tet) or 32 equal temperament (32et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 32 equal parts of exactly 37.5 ¢ each. Each step represents a frequency ratio of 21/32, or the 32nd root of 2.
Theory
32edo is generally the first power-of-2 edo which can be considered to handle low-limit just intonation at all. It has unambiguous mappings for primes up to the 11-limit, although 6/5 and Pythagorean intervals are especially poorly approximated if going by the patent val instead of using inconsistent approximations. Since 32edo is poor at approximating primes and it is a high power of 2, both traditional RTT and temperament-agnostic mos theory are of limited usefulness in the system (though it has an ultrasoft smitonic with L/s = 5/4). 32edo's 5:2:1 blackdye scale (1 5 2 5 1 5 2 5 1 5), which is melodically comparable to 31edo's 5:2:1 diasem, is notable for having 412.5¢ neogothic major thirds and 450¢ naiadics in place of the traditional 5-limit and Pythagorean major thirds in 5-limit blackdye, and the 75¢ semitone in place of 16/15. The 712.5¢ sharp fifth and the 675¢ flat fifth correspond to 3/2 and 40/27 in 5-limit blackdye, making 5:2:1 blackdye a dual-fifth scale.
As a tuning of other temperaments
While even advocates of less-common edos can struggle to find something about 32edo worth noting, it does provide an excellent tuning for the sixix temperament, which tempers out the 5-limit sixix comma, 3125/2916, using its 9\32 generator of size 337.5 cents. Petr Pařízek's preferred generator for sixix is (128/15)(1/11), which is 337.430 cents and which gives equal error to fifths and major thirds, so 32edo does sixix about as well as sixix can be done. It also can be used (with the 9\32 generator) to tune mohavila, an 11-limit temperament which does not temper out sixix.
It also tempers out 2048/2025 in the 5-limit, and 50/49 with 64/63 in the 7-limit, which means it supports pajara, with a very sharp fifth of 712.5 cents which could be experimented with by those with a penchant for fifths even sharper than the fifth of 27edo; this fifth is in fact very close to the minimax tuning of the pajara extension pajaro, using the 32f val. In the 11-limit it provides the optimal patent val for the 15 & 17 temperament, tempering out 55/54, 64/63, and 245/242.
The sharp fifth of 32edo can be used to generate a very unequal archy (specifically oceanfront) diatonic scale, with a diatonic semitone of 5 steps and a chromatic semitone of only 1. The diatonic major third (which can sound like both a major third and a flat fourth depending on context) is an interseptimal interval of 450¢, approximating 9/7 and 13/10, and the minor third is 262.5¢, approximating 7/6. Because of the unequalness of the scale, the minor second is reduced to a fifth-tone, but it still strongly resembles "normal" diatonic music, especially for darker modes. In addition to the sharp fifth, there is an alternative mavila-like flat fifth of 675 ¢ (inherited from 16edo), but it is much more inaccurate and discordant than the sharp fifth.
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +10.5 | -11.3 | +6.2 | -16.4 | +11.2 | -15.5 | -0.8 | +7.5 | +2.5 | +16.7 | +9.2 |
| Relative (%) | +28.1 | -30.2 | +16.5 | -43.8 | +29.8 | -41.4 | -2.0 | +20.1 | +6.6 | +44.6 | +24.6 | |
| Steps (reduced) |
51 (19) |
74 (10) |
90 (26) |
101 (5) |
111 (15) |
118 (22) |
125 (29) |
131 (3) |
136 (8) |
141 (13) |
145 (17) | |
Subsets and supersets
Since 32 factors into primes as 25, 32edo contains subset edos 2, 4, 8, and 16.
Intervals
| Degree | Cents | Ups and downs notation | 13-limit Ratios | Other | ||
|---|---|---|---|---|---|---|
| 0 | 0.0 | P1 | perfect unison | D | 1/1 | |
| 1 | 37.5 | ^1, m2 | up unison, minor 2nd | ^D, Eb | 49/48, 50/49, 45/44 | 46/45, 52/51, 51/50 |
| 2 | 75.0 | ^m2 | upminor 2nd | ^Eb | 22/21, 25/24 | 24/23, 23/22 |
| 3 | 112.5 | ^^m2 | dupminor 2nd | ^^Eb | 16/15 | 49/46 |
| 4 | 150.0 | vvM2 | dudmajor 2nd | vvE | 12/11, 49/45 | 25/23 |
| 5 | 187.5 | A1, vM2 | aug 1sn, downmajor 2nd | D#, vE | 10/9, 39/35 | 19/17 |
| 6 | 225.0 | M2 | major 2nd | E | 8/7, 25/22 | 57/50 |
| 7 | 262.5 | m3 | minor 3rd | F | 7/6, 64/55 | 57/49 |
| 8 | 300.0 | ^m3 | upminor 3rd | ^F | 6/5, 32/27 | 19/16 |
| 9 | 337.5 | ^^m3 | dupminor 3rd | ^^F | 11/9, 39/32, 63/52 | 17/14, 28/23 |
| 10 | 375.0 | vvM3 | dudmajor 3rd | vvF# | 5/4, 26/21, 56/45, 96/77 | 36/29 |
| 11 | 412.5 | vM3 | downmajor 3rd | vF# | 14/11, 33/26, 80/63 | 19/15 |
| 12 | 450.0 | M3 | major 3rd | F# | 13/10, 35/27, 64/49 | 22/17, 57/44 |
| 13 | 487.5 | P4 | perfect 4th | G | 4/3, 33/25, 160/121 | 45/34, 85/64 |
| 14 | 525.0 | ^4 | up 4th | ^G | 27/20, 110/81 | 19/14, 23/17 |
| 15 | 562.5 | ^^4, ^d5 | dup 4th, updim 5th | ^^G, ^Ab | 18/13, 11/8 | |
| 16 | 600.0 | vvA4, ^^d5 | dudaug 4th, dupdim 5th | vvG#, ^^Ab | 7/5, 10/7, 99/70, 140/99 | 17/12, 12/17 |
| 17 | 637.5 | vA4, vv5 | downaug 4th, dud 5th | vG#, vvA | 13/9, 16/11 | |
| 18 | 675.0 | v5 | down 5th | vA | 40/27, 81/55 | 28/19, 34/23 |
| 19 | 712.5 | P5 | perfect 5th | A | 3/2, 50/33, 121/80 | 68/45, 128/85 |
| 20 | 750.0 | m6 | minor 6th | Bb | 20/13, 54/35, 49/32 | 17/11, 88/57 |
| 21 | 787.5 | ^m6 | upminor 6th | ^Bb | 11/7, 52/33, 63/40 | 30/19 |
| 22 | 825.0 | ^^m6 | dupminor 6th | ^^Bb | 8/5, 21/13, 45/28, 77/48 | 29/18 |
| 23 | 862.5 | vvM6 | dudmajor 6th | vvB | 18/11, 64/39, 104/63 | 28/17, 23/14 |
| 24 | 900.0 | vM6 | downmajor 6th | vB | 5/3, 27/16 | 32/19 |
| 25 | 937.5 | M6 | major 6th | B | 12/7, 55/32 | 98/57 |
| 26 | 975.0 | m7 | minor 7th | C | 7/4, 44/25 | 100/57 |
| 27 | 1012.5 | ^m7 | upminor 7th | ^C | 9/5, 70/39 | 34/19 |
| 28 | 1050.0 | ^^m7 | dupminor 7th | ^^C | 11/6, 90/49 | 46/25 |
| 29 | 1087.5 | vvM7 | dudmajor 7th | vvC# | 15/8 | 92/49 |
| 30 | 1125.0 | vM7 | downmajor 7th | vC# | 21/11, 48/25 | 23/12, 44/23 |
| 31 | 1162.5 | M7, v8 | major 7th, down 8ve | C#, vD | 96/49, 49/25, 88/45 | 45/23, 51/26, 100/51 |
| 32 | 1200.0 | P8 | 8ve | D | 2/1 | |
Notation
Ups and downs notation
32edo can be notated with ups and downs, spoken as up, dup, dudsharp, downsharp, sharp, upsharp etc. and down, dud, dupflat etc. Note that dudsharp is equivalent to trup (triple-up) and dupflat is equivalent to trud (triple-down).
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |||||||||||||
| Flat symbol |
Another notation uses alternative ups and downs. Here, this can be done using sharps and flats with arrows, borrowed from extended Helmholtz–Ellis notation:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |||||||||||||
| Flat symbol |
If the arrows are taken to have their own layer of enharmonic spellings, then in some cases notes may be best denoted using triple arrows.
Sagittal notation
This notation uses the same sagittal sequence as 25-EDO, and is a subset of the notation for 64b.
Evo flavor

Revo flavor
Approximation to JI
The following tables show how 15-odd-limit intervals are represented in 32edo. Prime harmonics are in bold; inconsistent intervals are in italics.
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 11/6, 12/11 | 0.637 | 1.7 |
| 15/8, 16/15 | 0.769 | 2.0 |
| 13/9, 18/13 | 0.882 | 2.4 |
| 13/10, 20/13 | 4.214 | 11.2 |
| 7/6, 12/7 | 4.371 | 11.7 |
| 11/7, 14/11 | 5.008 | 13.4 |
| 9/5, 10/9 | 5.096 | 13.6 |
| 7/4, 8/7 | 6.174 | 16.5 |
| 15/14, 28/15 | 6.943 | 18.5 |
| 11/9, 18/11 | 9.908 | 26.4 |
| 3/2, 4/3 | 10.545 | 28.1 |
| 13/11, 22/13 | 10.790 | 28.8 |
| 11/8, 16/11 | 11.182 | 29.8 |
| 5/4, 8/5 | 11.314 | 30.2 |
| 13/12, 24/13 | 11.427 | 30.5 |
| 15/11, 22/15 | 11.951 | 31.9 |
| 15/13, 26/15 | 14.759 | 39.4 |
| 9/7, 14/9 | 14.916 | 39.8 |
| 11/10, 20/11 | 15.004 | 40.0 |
| 13/8, 16/13 | 15.528 | 41.4 |
| 5/3, 6/5 | 15.641 | 41.7 |
| 13/7, 14/13 | 15.798 | 42.1 |
| 9/8, 16/9 | 16.410 | 43.8 |
| 7/5, 10/7 | 17.488 | 46.6 |
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 11/6, 12/11 | 0.637 | 1.7 |
| 15/8, 16/15 | 0.769 | 2.0 |
| 13/10, 20/13 | 4.214 | 11.2 |
| 7/6, 12/7 | 4.371 | 11.7 |
| 11/7, 14/11 | 5.008 | 13.4 |
| 7/4, 8/7 | 6.174 | 16.5 |
| 15/14, 28/15 | 6.943 | 18.5 |
| 11/9, 18/11 | 9.908 | 26.4 |
| 3/2, 4/3 | 10.545 | 28.1 |
| 11/8, 16/11 | 11.182 | 29.8 |
| 5/4, 8/5 | 11.314 | 30.2 |
| 15/11, 22/15 | 11.951 | 31.9 |
| 15/13, 26/15 | 14.759 | 39.4 |
| 9/7, 14/9 | 14.916 | 39.8 |
| 13/8, 16/13 | 15.528 | 41.4 |
| 7/5, 10/7 | 17.488 | 46.6 |
| 9/8, 16/9 | 21.090 | 56.2 |
| 13/7, 14/13 | 21.702 | 57.9 |
| 5/3, 6/5 | 21.859 | 58.3 |
| 11/10, 20/11 | 22.496 | 60.0 |
| 13/12, 24/13 | 26.073 | 69.5 |
| 13/11, 22/13 | 26.710 | 71.2 |
| 9/5, 10/9 | 32.404 | 86.4 |
| 13/9, 18/13 | 36.618 | 97.6 |
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3 | [51 -32⟩ | [⟨32 51]] | -3.327 | 3.32 | 8.87 |
| 2.3.7 | 64/63, 46118408/43046721 | [⟨32 51 90]] | -2.950 | 2.76 | 7.38 |
| 2.3.5 | 648/625, 20480/19683 | [⟨32 51 75]] (32c) | -5.965 | 4.61 | 12.3 |
| 2.3.5.7 | 64/63, 245/243, 392/375 | [⟨32 51 75 90]] (32c) | -5.027 | 4.31 | 11.5 |
| 2.3.5 | 2048/2025, 3125/2916 | [⟨32 51 74]] (32) | +0.177 | 4.72 | 12.6 |
| 2.3.5.7 | 50/49, 64/63, 3125/2916 | [⟨32 51 75 90]] (32) | -1.008 | 4.15 | 11.1 |
Rank-2 temperaments
| Periods per 8ve |
Generator* | Cents* | Associated ratio* |
Temperaments |
|---|---|---|---|---|
| 1 | 1\32 | 37.5 | 49/48 | Slender (32) |
| 1 | 9\32 | 262.5 | 7/6 | Septimin (32f) |
| 1 | 9\32 | 337.5 | 6/5 | Sixix (32f) |
| 1 | 13\32 | 487.5 | 4/3 | Superpyth (32c, 7-limit) / ultrapyth (32) / quasiultra (32) |
| 1 | 15\32 | 562.5 | 7/5 | Progress (32cf) |
| 2 | 13\32 | 487.5 | 4/3 | Pajara (32, 7-limit) |
| 8 | 14\33 (1\32) |
487.5 (37.5) |
4/3 (36/35) |
Octonion (32cf) |
| 16 | 14\33 (1\32) |
487.5 (37.5) |
4/3 (45/44) |
Sedecic (32) |
* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct
Delta-rational harmony
The tables below show chords that approximate 3-integer-limit delta-rational chords with least-squares error less than 0.0015.
| Steps | Delta signature | Least-squares error |
|---|---|---|
| 0,1,2 | +1+1 | 0.00023 |
| 0,1,3 | +1+2 | 0.00051 |
| 0,1,4 | +1+3 | 0.00083 |
| 0,2,3 | +2+1 | 0.00041 |
| 0,2,4 | +1+1 | 0.00092 |
| 0,3,4 | +3+1 | 0.00060 |
| 0,3,11 | +1+3 | 0.00014 |
| 0,4,11 | +1+2 | 0.00087 |
| 0,5,8 | +3+2 | 0.00076 |
| 0,6,16 | +1+2 | 0.00076 |
| 0,8,26 | +1+3 | 0.00016 |
| 0,9,23 | +1+2 | 0.00000 |
| 0,12,17 | +2+1 | 0.00004 |
| 0,13,20 | +3+2 | 0.00008 |
| 0,15,21 | +2+1 | 0.00007 |
| 0,18,27 | +3+2 | 0.00000 |
| 0,22,30 | +2+1 | 0.00030 |
| 0,25,31 | +3+1 | 0.00062 |
| Steps | Delta signature | Least-squares error |
|---|---|---|
| 0,1,2,3 | +1+?+1 | 0.00056 |
| 0,1,2,4 | +1+?+2 | 0.00100 |
| 0,1,3,4 | +1+?+1 | 0.00085 |
| 0,1,16,17 | +2+?+3 | 0.00091 |
| 0,1,16,18 | +1+?+3 | 0.00093 |
| 0,1,17,18 | +2+?+3 | 0.00058 |
| 0,1,17,19 | +1+?+3 | 0.00051 |
| 0,1,18,19 | +2+?+3 | 0.00025 |
| 0,1,18,20 | +1+?+3 | 0.00009 |
| 0,1,19,20 | +2+?+3 | 0.00010 |
| 0,1,19,21 | +1+?+3 | 0.00034 |
| 0,1,20,21 | +2+?+3 | 0.00045 |
| 0,1,20,22 | +1+?+3 | 0.00078 |
| 0,1,21,22 | +2+?+3 | 0.00081 |
| 0,1,30,31 | +1+?+2 | 0.00076 |
| 0,2,3,4 | +2+?+1 | 0.00082 |
| 0,2,6,11 | +1+?+3 | 0.00077 |
| 0,2,7,12 | +1+?+3 | 0.00009 |
| 0,2,8,13 | +1+?+3 | 0.00097 |
| 0,2,12,13 | +3+?+2 | 0.00072 |
| 0,2,12,15 | +1+?+2 | 0.00060 |
| 0,2,13,14 | +3+?+2 | 0.00032 |
| 0,2,13,16 | +1+?+2 | 0.00018 |
| 0,2,14,15 | +3+?+2 | 0.00009 |
| 0,2,14,17 | +1+?+2 | 0.00097 |
| 0,2,15,16 | +3+?+2 | 0.00050 |
| 0,2,16,17 | +3+?+2 | 0.00093 |
| 0,2,17,21 | +1+?+3 | 0.00061 |
| 0,2,18,20 | +2+?+3 | 0.00050 |
| 0,2,18,22 | +1+?+3 | 0.00025 |
| 0,2,19,21 | +2+?+3 | 0.00020 |
| 0,2,20,22 | +2+?+3 | 0.00091 |
| 0,3,4,8 | +2+?+3 | 0.00098 |
| 0,3,5,9 | +2+?+3 | 0.00007 |
| 0,3,7,12 | +1+?+2 | 0.00048 |
| 0,3,8,13 | +1+?+2 | 0.00071 |
| 0,3,9,16 | +1+?+3 | 0.00074 |
| 0,3,10,17 | +1+?+3 | 0.00057 |
| 0,3,17,23 | +1+?+3 | 0.00026 |
| 0,3,18,19 | +2+?+1 | 0.00082 |
| 0,3,18,21 | +2+?+3 | 0.00075 |
| 0,3,18,22 | +1+?+2 | 0.00025 |
| 0,3,19,20 | +2+?+1 | 0.00035 |
| 0,3,19,21 | +1+?+1 | 0.00019 |
| 0,3,19,22 | +2+?+3 | 0.00030 |
| 0,3,19,23 | +1+?+2 | 0.00094 |
| 0,3,20,21 | +2+?+1 | 0.00013 |
| 0,3,20,22 | +1+?+1 | 0.00066 |
| 0,3,21,22 | +2+?+1 | 0.00063 |
| 0,3,26,31 | +1+?+3 | 0.00016 |
| 0,4,5,12 | +1+?+2 | 0.00059 |
| 0,4,5,15 | +1+?+3 | 0.00060 |
| 0,4,8,13 | +2+?+3 | 0.00013 |
| 0,4,11,20 | +1+?+3 | 0.00049 |
| 0,4,12,18 | +1+?+2 | 0.00042 |
| 0,4,13,14 | +3+?+1 | 0.00079 |
| 0,4,13,16 | +1+?+1 | 0.00088 |
| 0,4,14,15 | +3+?+1 | 0.00035 |
| 0,4,14,16 | +3+?+2 | 0.00024 |
| 0,4,14,17 | +1+?+1 | 0.00024 |
| 0,4,15,16 | +3+?+1 | 0.00009 |
| 0,4,15,17 | +3+?+2 | 0.00060 |
| 0,4,16,17 | +3+?+1 | 0.00055 |
| 0,4,17,25 | +1+?+3 | 0.00058 |
| 0,4,19,23 | +2+?+3 | 0.00040 |
| 0,4,21,26 | +1+?+2 | 0.00030 |
| 0,4,23,30 | +1+?+3 | 0.00062 |
| 0,5,6,9 | +3+?+2 | 0.00013 |
| 0,5,7,19 | +1+?+3 | 0.00069 |
| 0,5,9,17 | +1+?+2 | 0.00047 |
| 0,5,10,16 | +2+?+3 | 0.00038 |
| 0,5,11,13 | +2+?+1 | 0.00067 |
| 0,5,11,15 | +1+?+1 | 0.00027 |
| 0,5,11,22 | +1+?+3 | 0.00052 |
| 0,5,12,14 | +2+?+1 | 0.00015 |
| 0,5,13,15 | +2+?+1 | 0.00099 |
| 0,5,15,22 | +1+?+2 | 0.00090 |
| 0,5,16,26 | +1+?+3 | 0.00034 |
| 0,5,19,24 | +2+?+3 | 0.00051 |
| 0,5,23,29 | +1+?+2 | 0.00015 |
| 0,5,24,25 | +3+?+1 | 0.00090 |
| 0,5,24,27 | +1+?+1 | 0.00085 |
| 0,5,25,26 | +3+?+1 | 0.00034 |
| 0,5,25,27 | +3+?+2 | 0.00011 |
| 0,5,25,28 | +1+?+1 | 0.00058 |
| 0,5,26,27 | +3+?+1 | 0.00023 |
| 0,5,26,28 | +3+?+2 | 0.00096 |
| 0,5,27,28 | +3+?+1 | 0.00081 |
| 0,6,9,14 | +1+?+1 | 0.00013 |
| 0,6,11,18 | +2+?+3 | 0.00020 |
| 0,6,12,21 | +1+?+2 | 0.00064 |
| 0,6,15,18 | +3+?+2 | 0.00025 |
| 0,6,18,26 | +1+?+2 | 0.00075 |
| 0,6,19,25 | +2+?+3 | 0.00062 |
| 0,6,20,22 | +2+?+1 | 0.00074 |
| 0,6,20,24 | +1+?+1 | 0.00046 |
| 0,6,20,31 | +1+?+3 | 0.00043 |
| 0,6,21,23 | +2+?+1 | 0.00025 |
| 0,6,24,31 | +1+?+2 | 0.00091 |
| 0,7,8,12 | +3+?+2 | 0.00097 |
| 0,7,8,14 | +1+?+1 | 0.00076 |
| 0,7,8,24 | +1+?+3 | 0.00043 |
| 0,7,9,11 | +3+?+1 | 0.00053 |
| 0,7,9,12 | +2+?+1 | 0.00018 |
| 0,7,9,13 | +3+?+2 | 0.00054 |
| 0,7,9,20 | +1+?+2 | 0.00020 |
| 0,7,10,12 | +3+?+1 | 0.00028 |
| 0,7,12,20 | +2+?+3 | 0.00010 |
| 0,7,14,24 | +1+?+2 | 0.00004 |
| 0,7,15,29 | +1+?+3 | 0.00028 |
| 0,7,17,22 | +1+?+1 | 0.00091 |
| 0,7,19,26 | +2+?+3 | 0.00073 |
| 0,7,22,25 | +3+?+2 | 0.00065 |
| 0,7,23,26 | +3+?+2 | 0.00086 |
| 0,7,27,31 | +1+?+1 | 0.00074 |
| 0,7,28,30 | +2+?+1 | 0.00044 |
| 0,7,29,31 | +2+?+1 | 0.00074 |
| 0,8,11,23 | +1+?+2 | 0.00070 |
| 0,8,11,28 | +1+?+3 | 0.00080 |
| 0,8,13,22 | +2+?+3 | 0.00070 |
| 0,8,14,20 | +1+?+1 | 0.00072 |
| 0,8,15,19 | +3+?+2 | 0.00057 |
| 0,8,16,18 | +3+?+1 | 0.00031 |
| 0,8,16,19 | +2+?+1 | 0.00023 |
| 0,8,16,27 | +1+?+2 | 0.00085 |
| 0,8,17,19 | +3+?+1 | 0.00063 |
| 0,8,19,27 | +2+?+3 | 0.00084 |
| 0,8,23,28 | +1+?+1 | 0.00055 |
| 0,9,10,15 | +3+?+2 | 0.00092 |
| 0,9,11,30 | +1+?+3 | 0.00012 |
| 0,9,13,20 | +1+?+1 | 0.00100 |
| 0,9,13,26 | +1+?+2 | 0.00021 |
| 0,9,17,29 | +1+?+2 | 0.00062 |
| 0,9,19,28 | +2+?+3 | 0.00096 |
| 0,9,20,26 | +1+?+1 | 0.00070 |
| 0,9,21,25 | +3+?+2 | 0.00055 |
| 0,9,22,24 | +3+?+1 | 0.00031 |
| 0,9,22,25 | +2+?+1 | 0.00034 |
| 0,9,23,25 | +3+?+1 | 0.00077 |
| 0,10,13,17 | +2+?+1 | 0.00066 |
| 0,10,14,25 | +2+?+3 | 0.00076 |
| 0,10,16,21 | +3+?+2 | 0.00034 |
| 0,10,18,25 | +1+?+1 | 0.00004 |
| 0,10,27,29 | +3+?+1 | 0.00080 |
| 0,10,27,30 | +2+?+1 | 0.00029 |
| 0,10,27,31 | +3+?+2 | 0.00077 |
| 0,10,28,30 | +3+?+1 | 0.00040 |
| 0,11,12,18 | +3+?+2 | 0.00040 |
| 0,11,12,28 | +1+?+2 | 0.00038 |
| 0,11,13,16 | +3+?+1 | 0.00049 |
| 0,11,14,17 | +3+?+1 | 0.00085 |
| 0,11,14,26 | +2+?+3 | 0.00077 |
| 0,11,16,24 | +1+?+1 | 0.00085 |
| 0,11,18,22 | +2+?+1 | 0.00057 |
| 0,11,21,26 | +3+?+2 | 0.00058 |
| 0,11,23,30 | +1+?+1 | 0.00023 |
| 0,12,15,24 | +1+?+1 | 0.00060 |
| 0,12,18,21 | +3+?+1 | 0.00014 |
| 0,12,21,29 | +1+?+1 | 0.00078 |
| 0,12,23,27 | +2+?+1 | 0.00036 |
| 0,12,25,30 | +3+?+2 | 0.00084 |
| 0,13,16,21 | +2+?+1 | 0.00057 |
| 0,13,19,28 | +1+?+1 | 0.00023 |
| 0,13,22,25 | +3+?+1 | 0.00019 |
| 0,13,27,31 | +2+?+1 | 0.00012 |
| 0,14,15,30 | +2+?+3 | 0.00004 |
| 0,14,17,24 | +3+?+2 | 0.00028 |
| 0,14,20,25 | +2+?+1 | 0.00048 |
| 0,14,26,29 | +3+?+1 | 0.00012 |
| 0,15,16,20 | +3+?+1 | 0.00002 |
| 0,15,24,29 | +2+?+1 | 0.00028 |
| 0,16,20,31 | +1+?+1 | 0.00042 |
| 0,16,24,31 | +3+?+2 | 0.00051 |
| 0,17,21,29 | +3+?+2 | 0.00090 |
| 0,17,22,28 | +2+?+1 | 0.00062 |
| 0,17,23,27 | +3+?+1 | 0.00039 |
| 0,18,25,31 | +2+?+1 | 0.00007 |
| 0,18,26,30 | +3+?+1 | 0.00001 |
| 0,19,21,30 | +3+?+2 | 0.00014 |
| 0,20,21,26 | +3+?+1 | 0.00032 |
| 0,21,24,29 | +3+?+1 | 0.00026 |
Octave stretch or compression
What follows is a comparison of compressed-octave 32edo tunings.
- 32edo
- Step size: 37.500 ¢, octave size: 1200.0 ¢
Pure-octaves 32edo approximates all harmonics up to 16 within 15.5 ¢.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | +10.5 | +0.0 | -11.3 | +10.5 | +6.2 | +0.0 | -16.4 | -11.3 | +11.2 | +10.5 |
| Relative (%) | +0.0 | +28.1 | +0.0 | -30.2 | +28.1 | +16.5 | +0.0 | -43.8 | -30.2 | +29.8 | +28.1 | |
| Steps (reduced) |
32 (0) |
51 (19) |
64 (0) |
74 (10) |
83 (19) |
90 (26) |
96 (0) |
101 (5) |
106 (10) |
111 (15) |
115 (19) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -15.5 | +6.2 | -0.8 | +0.0 | +7.5 | -16.4 | +2.5 | -11.3 | +16.7 | +11.2 | +9.2 | +10.5 |
| Relative (%) | -41.4 | +16.5 | -2.0 | +0.0 | +20.1 | -43.8 | +6.6 | -30.2 | +44.6 | +29.8 | +24.6 | +28.1 | |
| Steps (reduced) |
118 (22) |
122 (26) |
125 (29) |
128 (0) |
131 (3) |
133 (5) |
136 (8) |
138 (10) |
141 (13) |
143 (15) |
145 (17) |
147 (19) | |
- Step size: 37.481 ¢, octave size: 1199.4 ¢
Compressing the octave of 32edo by around half a cent results in improved primes 3, 7 and 11, but worse primes 5 and 13. This approximates all harmonics up to 16 within 18.3 ¢. Its 13-limit WE tuning and 13-limit TE tuning both do this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -0.6 | +9.6 | -1.2 | -12.7 | +9.0 | +4.5 | -1.8 | -18.3 | -13.3 | +9.1 | +8.4 |
| Relative (%) | -1.6 | +25.5 | -3.2 | -33.9 | +23.9 | +11.9 | -4.9 | -48.9 | -35.6 | +24.2 | +22.3 | |
| Step | 32 | 51 | 64 | 74 | 83 | 90 | 96 | 101 | 106 | 111 | 115 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -17.8 | +3.9 | -3.1 | -2.4 | +5.1 | +18.5 | -0.1 | -13.9 | +14.0 | +8.5 | +6.5 | +7.8 |
| Relative (%) | -47.4 | +10.3 | -8.4 | -6.5 | +13.5 | +49.5 | -0.3 | -37.2 | +37.5 | +22.6 | +17.3 | +20.7 | |
| Step | 118 | 122 | 125 | 128 | 131 | 134 | 136 | 138 | 141 | 143 | 145 | 147 | |
- Step size: 37.453 ¢, octave size: 1198.5 ¢
Compressing the octave of 32edo by around 1.5 ¢ results in improved primes 3, 7 and 11, but worse primes 2, 5 and 13. This approximates all harmonics up to 16 within 16.4 ¢. Its 11-limit WE tuning and 11-limit TE tuning both do this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -1.5 | +8.1 | -3.0 | -14.8 | +6.6 | +1.9 | -4.5 | +16.3 | -16.3 | +6.0 | +5.1 |
| Relative (%) | -4.0 | +21.8 | -8.0 | -39.5 | +17.7 | +5.2 | -12.0 | +43.5 | -43.5 | +15.9 | +13.7 | |
| Step | 32 | 51 | 64 | 74 | 83 | 90 | 96 | 102 | 106 | 111 | 115 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +16.4 | +0.4 | -6.6 | -6.0 | +1.4 | +14.8 | -3.9 | -17.8 | +10.1 | +4.5 | +2.4 | +3.6 |
| Relative (%) | +43.7 | +1.2 | -17.7 | -16.1 | +3.7 | +39.5 | -10.4 | -47.5 | +26.9 | +11.9 | +6.4 | +9.7 | |
| Step | 119 | 122 | 125 | 128 | 131 | 134 | 136 | 138 | 141 | 143 | 145 | 147 | |
- Step size: 37.431 ¢, octave size: 1197.8 ¢
Compressing the octave of 32edo by around 2 ¢ results in improved primes 3, 7, 11 and 13, but worse primes 2 and 5. This approximates all harmonics up to 16 within 18.6 ¢. If one wishes to use both of 32edo's mappings of the 5th harmonic simultaneously, this tuning is suited to that due to evenly sharing the error between them. The tuning 90ed7 does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -2.2 | +7.0 | -4.4 | -16.4 | +4.9 | +0.0 | -6.6 | +14.1 | -18.6 | +3.6 | +2.7 |
| Relative (%) | -5.9 | +18.8 | -11.7 | -43.8 | +13.0 | +0.0 | -17.6 | +37.6 | -49.7 | +9.5 | +7.1 | |
| Steps (reduced) |
32 (32) |
51 (51) |
64 (64) |
74 (74) |
83 (83) |
90 (0) |
96 (6) |
102 (12) |
106 (16) |
111 (21) |
115 (25) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +13.8 | -2.2 | -9.3 | -8.8 | -1.4 | +11.9 | -6.8 | +16.7 | +7.0 | +1.4 | -0.7 | +0.5 |
| Relative (%) | +36.9 | -5.9 | -25.0 | -23.5 | -3.9 | +31.8 | -18.3 | +44.5 | +18.8 | +3.7 | -1.9 | +1.2 | |
| Steps (reduced) |
119 (29) |
122 (32) |
125 (35) |
128 (38) |
131 (41) |
134 (44) |
136 (46) |
139 (49) |
141 (51) |
143 (53) |
145 (55) |
147 (57) | |
- Step size: 37.418 ¢, octave size: 1197.375 ¢
Compressing the octave of 32edo by around NNN ¢ results in improved primes 3, 7, 11 and 13, but worse primes 2 and 5. This approximates all harmonics up to 16 within 17.4 ¢. The tuning 133zpi does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -2.6 | +6.4 | -5.2 | -17.4 | +3.7 | -1.2 | -7.9 | +12.7 | +17.4 | +2.1 | +1.1 |
| Relative (%) | -7.0 | +17.0 | -14.0 | -46.5 | +10.0 | -3.2 | -21.0 | +34.0 | +46.5 | +5.6 | +3.0 | |
| Step | 32 | 51 | 64 | 74 | 83 | 90 | 96 | 102 | 107 | 111 | 115 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +12.2 | -3.8 | -11.0 | -10.5 | -3.2 | +10.1 | -8.7 | +14.8 | +5.2 | -0.5 | -2.7 | -1.5 |
| Relative (%) | +32.6 | -10.2 | -29.4 | -28.1 | -8.5 | +27.0 | -23.2 | +39.5 | +13.8 | -1.5 | -7.1 | -4.0 | |
| Step | 119 | 122 | 125 | 128 | 131 | 134 | 136 | 139 | 141 | 143 | 145 | 147 | |
Below is a plot of the Zeta function, showing how its peak (ie biggest absolute value) is shifted above 32, corresponding to a zeta tuning with octaves flattened to 1197.375 cents. This will improve the fifth, at the expense of the third.
- Step size: 37.293 ¢, octave size: 1193.4 ¢
Compressing the octave of 32edo by around 6.5 ¢ results in improved primes 3, 5 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 18.2 ¢. The tuning 51edt does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -6.6 | +0.0 | -13.2 | +10.7 | -6.6 | -12.4 | +17.4 | +0.0 | +4.1 | -11.8 | -13.2 |
| Relative (%) | -17.7 | +0.0 | -35.5 | +28.6 | -17.7 | -33.3 | +46.8 | +0.0 | +10.9 | -31.6 | -35.5 | |
| Steps (reduced) |
32 (32) |
51 (0) |
64 (13) |
75 (24) |
83 (32) |
90 (39) |
97 (46) |
102 (0) |
107 (5) |
111 (9) |
115 (13) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -2.6 | +18.2 | +10.7 | +10.8 | +17.8 | -6.6 | +11.7 | -2.6 | -12.4 | -18.4 | +16.5 | +17.4 |
| Relative (%) | -7.1 | +48.9 | +28.6 | +29.0 | +47.6 | -17.7 | +31.3 | -6.8 | -33.3 | -49.3 | +44.3 | +46.8 | |
| Steps (reduced) |
119 (17) |
123 (21) |
126 (24) |
129 (27) |
132 (30) |
134 (32) |
137 (35) |
139 (37) |
141 (39) |
143 (41) |
146 (44) |
148 (46) | |
Instruments
Music
- Beyond the Grid (2024)
- "Zinnia Riplet" (32-EDO) (featured in Possible Worlds Vol. 4 of Spectropol Records)
- Admin's Hot Tub