14edo: Difference between revisions
Wikispaces>genewardsmith **Imported revision 215622076 - Original comment: ** |
m Text replacement - "Ups and Downs Notation" to "Ups and downs notation" |
||
| (225 intermediate revisions by 52 users not shown) | |||
| Line 1: | Line 1: | ||
{{interwiki | |||
| de = | |||
| en = 14edo | |||
| es = | |||
| ja = 14平均律 | |||
}} | |||
{{Infobox ET}} | |||
{{ED intro}} | |||
== Theory == | |||
The character of 14edo does not well serve those seeking low-[[limit]] JI approaches, with the exception of [[Subgroup|5:7:9:11:17:19]] (which is quite well approximated, relative to other JI approximations of the low-numbered edos). However, the [[ratio]]s 7/5, 7/6, 9/7, 10/7, 10/9, 11/7, 11/9, and 11/10 are all recognizably approximated, and if you accept that 14edo offers approximations of these intervals, you end up with a low-complexity, high-damage [[11-limit]] temperament where the [[comma]]s listed later in this page are [[tempered out]]. This leads to some of the bizarre equivalences described in the second "Approximate ratios" column in the table. | |||
14et has quite a bit of [[xenharmonic]] appeal, in a similar way to [[17edo|17et]], on account of having three types of 3rd and three types of 6th, rather than the usual two of [[12et]]. Since 14et also has a recognizable 4th and 5th, this makes it good for those wishing to explore alternative triadic harmonies without adding significantly more notes. It possesses a [[triad]]-rich 9-note [[mos scale]] of [[5L 4s]], wherein 7 of 9 notes are [[tonic]] to a subminor, supermajor, and/or neutral triad. | |||
14edo contains an [[omnidiatonic]] scale that can replace the standard diatonic scale, allowing for recognizable triadic harmony using the chords [[6:7:9]] and [[14:18:21]], as well as a neutral chord which can be seen as [[2:sqrt(6):3]]. | |||
=== Prime harmonics === | |||
{{Harmonics in equal|14}} | |||
=== Octave stretch === | |||
[[ | 14edo benefits from [[octave stretch]] as harmonics 3, 7, and 11 are all tuned flat. [[22edt]], [[36ed6]] and [[42zpi]] are among the possible choices. | ||
=== Subsets and supersets === | |||
Since 14 factors into primes as 2 × 7, 14edo contains [[2edo]] and [[7edo]] as subsets. | |||
== Notation == | |||
=== Ups and downs notation === | |||
{| class="wikitable center-all right-3" | |||
|- | |||
! Steps | |||
! Cents | |||
! Approximate<br>[[Harmonic]]s | |||
! Approximate<br>Ratios 1 <ref group="note">{{sg|limit=2.7/5.9/5.11/5.17/5.19/5 [[subgroup]]}}</ref> | |||
! Approximate<br>Ratios 2 <ref group="note">Based on treating 14edo as an 11-limit temperament of {{val| 14 22 32 39 48}} (14c).</ref> | |||
! Approximate<br>Ratios 3 <ref group="note">Nearest 15-odd-limit intervals by [[direct approximation]].</ref> | |||
! colspan="3" | [[Ups and downs notation]] | |||
! Interval Type | |||
! Audio | |||
|- | |||
| 0 | |||
| 0.000 | |||
| 1 | |||
| 1/1 | |||
| 1/1 | |||
| 1/1 | |||
| unison | |||
| 1 | |||
| D | |||
| Unison | |||
| [[File:piano_0_1edo.mp3]] | |||
|- | |||
| 1 | |||
| 85.714 | |||
| 67 | |||
| 20/19, 19/18, 18/17 | |||
| 28/27, 22/21, 21/20 | |||
| | |||
| up-unison,<br>down-2nd | |||
| ^1, v2 | |||
| ^D, vE | |||
| Narrow Minor 2nd | |||
| [[File:piano_1_14edo.mp3]] | |||
|- | |||
| 2 | |||
| 171.429 | |||
| 71 | |||
| 11/10, 10/9, 19/17 | |||
| 12/11, 11/10, 10/9, 9/8 | |||
| 11/10, 10/9 | |||
| 2nd | |||
| 2 | |||
| E | |||
| Neutral 2nd | |||
| [[File:piano_1_7edo.mp3]] | |||
|- | |||
| 3 | |||
| 257.143 | |||
| 37 | |||
| 22/19, 20/17 | |||
| 8/7, 7/6 | |||
| 15/13, 7/6 | |||
| up-2nd,<br>down-3rd | |||
| ^2, v3 | |||
| ^E, vF | |||
| Subminor 3rd | |||
| [[File:piano_3_14edo.mp3]] | |||
|- | |||
| 4 | |||
| 342.857 | |||
| 39 | |||
| 17/14, 11/9 | |||
| 6/5, 11/9, 5/4 | |||
| 11/9 | |||
| 3rd | |||
| 3 | |||
| F | |||
| Neutral 3rd | |||
| [[File:piano_2_7edo.mp3]] | |||
|- | |||
| 5 | |||
| 428.571 | |||
| 41 | |||
| 22/17, 14/11, 9/7 | |||
| 14/11, 9/7 | |||
| 14/11, 9/7 | |||
| up-3rd,<br>down-4th | |||
| ^3, v4 | |||
| ^F, vG | |||
| Supermajor 3rd | |||
| [[File:piano_5_14edo.mp3]] | |||
|- | |||
| 6 | |||
| 514.286 | |||
| 43 | |||
| 19/14 | |||
| 4/3, 15/11, 11/8 | |||
| 4/3 | |||
| 4th | |||
| 4 | |||
| G | |||
| Wide 4th | |||
| [[File:piano_3_7edo.mp3]] | |||
|- | |||
| 7 | |||
| 600.000 | |||
| 91 | |||
| 7/5, 10/7 | |||
| 7/5, 10/7 | |||
| 7/5, 10/7 | |||
| up-4th,<br>down-5th | |||
| ^4, v5 | |||
| ^G, vA | |||
| Tritone | |||
| [[File:piano_1_2edo.mp3]] | |||
|- | |||
| 8 | |||
| 685.714 | |||
| 95 | |||
| 28/19 | |||
| 16/11, 22/15, 3/2 | |||
| 3/2 | |||
| 5th | |||
| 5 | |||
| A | |||
| Narrow 5th | |||
| [[File:piano_4_7edo.mp3]] | |||
|- | |||
| 9 | |||
| 771.429 | |||
| 25 | |||
| 14/9, 11/7, 17/11 | |||
| 14/9, 11/7 | |||
| 14/9, 11/7 | |||
| up-5th,<br>down-6th | |||
| ^5, v6 | |||
| ^A, vB | |||
| Subminor 6th | |||
| [[File:piano_9_14edo.mp3]] | |||
|- | |||
| 10 | |||
| 857.143 | |||
| 105 | |||
| 18/11, 28/17 | |||
| 8/5, 18/11, 5/3 | |||
| 18/11 | |||
| 6th | |||
| 6 | |||
| B | |||
| Neutral 6th | |||
| [[File:piano_5_7edo.mp3]] | |||
|- | |||
| 11 | |||
| 942.857 | |||
| 55 | |||
| 17/10, 19/11 | |||
| 12/7, 7/4 | |||
| 12/7, 26/15 | |||
| up-6th,<br>down-7th | |||
| ^6, v7 | |||
| ^B, vC | |||
| Supermajor 6th | |||
| [[File:piano_11_14edo.mp3]] | |||
|- | |||
| 12 | |||
| 1028.571 | |||
| 29 | |||
| 19/34, 9/5, 20/11 | |||
| 16/9, 9/5, 20/11, 11/6 | |||
| 9/5, 20/11 | |||
| 7th | |||
| 7 | |||
| C | |||
| Neutral 7th | |||
| [[File:piano_6_7edo.mp3]] | |||
|- | |||
| 13 | |||
| 1114.286 | |||
| 61 | |||
| 17/9, 36/19, 19/10 | |||
| 40/21, 21/11, 27/14 | |||
| | |||
| up-7th,<br />down-8ve | |||
| ^7, v8 | |||
| ^C, vD | |||
| Wide Major 7th | |||
| [[File:piano_13_14edo.mp3]] | |||
|- | |||
| 14 | |||
| 1200.000 | |||
| 2 | |||
| 2/1 | |||
| 2/1 | |||
| 2/1 | |||
| 8ve | |||
| 8 | |||
| D | |||
| Octave | |||
| [[File:piano_1_1edo.mp3]] | |||
|} | |||
<references group="note" /> | |||
=== Sagittal notation === | |||
This notation uses the same sagittal sequence as [[9edo#Sagittal notation|9-EDO]], is a subset of the notations for EDOs [[28edo#Sagittal notation|28]] and [[42edo#Second-best fifth notation|42b]], and is a superset of the notation for [[7edo#Sagittal notation|7-EDO]]. | |||
<imagemap> | |||
File:14-EDO_Sagittal.svg | |||
desc none | |||
5 | rect 80 0 300 50 [[Sagittal_notation]] | ||
5 | rect 423 0 583 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation] | ||
4 4 | rect 20 80 423 106 [[Fractional_3-limit_notation#Bad-fifths_limma-fraction_notation | limma-fraction notation]] | ||
3 3 | default [[File:14-EDO_Sagittal.svg]] | ||
</imagemap> | |||
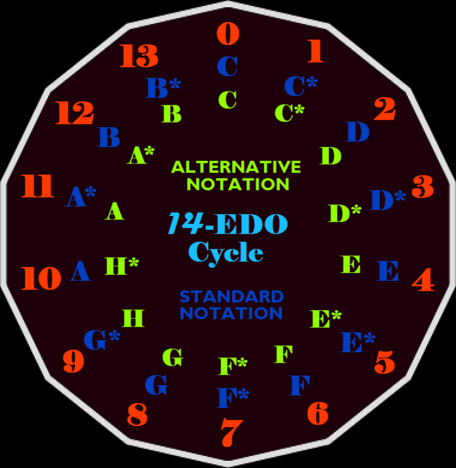
2 | === Ivor Darreg's notation === | ||
3 | [[Ivor Darreg]] wrote in [http://www.tonalsoft.com/sonic-arts/darreg/dar15.htm this article]: | ||
3 | ''The 14-tone scale presents a new situation: while one might use ordinary sharps and flats in addition to conventional naturals for the notes of the 7-tone-equal temperament, it would be misleading and confusing to do so, because there is a 7-tone circle of fifths (admittedly quite distorted) already notatable and nameable as F C G D A E B in the usual manner. But there is no 14-tone circle of fifths. There is simply a second set of 7 fifths in a circle which does not intersect the with the first set. Thus is we think of B-flat and B, or B-natural and F-sharp, the 14-tone-system interval would NOT be a fifth of that system and would not sound like one, since B F would be the very same kind of distorted fifth that C G or A E happens to be in 7 or 14. Our suggestion is to call the new notes of 14, the second set of 7, F* C* G* D* A* E* B*, and use asterisks or arrows or whatever you please on the staff. Or just number the tones as for 13.'' | ||
2 | |||
The following chart (made by [[Tútim Dennsuul Wafiil|TDW]]) shows this recommendation as "standard notation" as well as a proposed alternative. | |||
2 2 | |||
{| class="wikitable" | |||
|- | |||
| [[File:Ciclo_Tetradecafonía.png|alt=Ciclo_Tetradecafonía.png|456x468px|Ciclo_Tetradecafonía.png]] | |||
|- | |||
| Intervallic Cycle of 14 steps Equal per Octave | |||
2 | |} | ||
== Chord names == | |||
Ups and downs can be used to name 14edo chords. Because every interval is perfect, the quality can be omitted, and the words major, minor, augmented and diminished are never used. Alterations are always enclosed in parentheses, additions never are. An up or down immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13). | |||
0-4-8 = C E G = C = C or C perfect<br> | |||
0-3-8 = C vE G = Cv = C down<br> | |||
0-5-8 = C ^E G = C^ = C up<br> | |||
0-4-7 = C E vG = C(v5) = C down-five<br> | |||
0-5-9 = C ^E ^G = C^(^5) = C up up-five<br> | |||
0-4-8-12 = C E G B = C7 = C seven<br> | |||
0-4-8-11 = C E G vB = C,v7 = C add down-seven<br> | |||
0-3-8-12 = C vE G B = Cv,7 = C down add seven<br> | |||
0-3-8-11 = C vE G vB = Cv7 = C down-seven | |||
For a more complete list, see [[Ups and downs notation #Chords and Chord Progressions]]. | |||
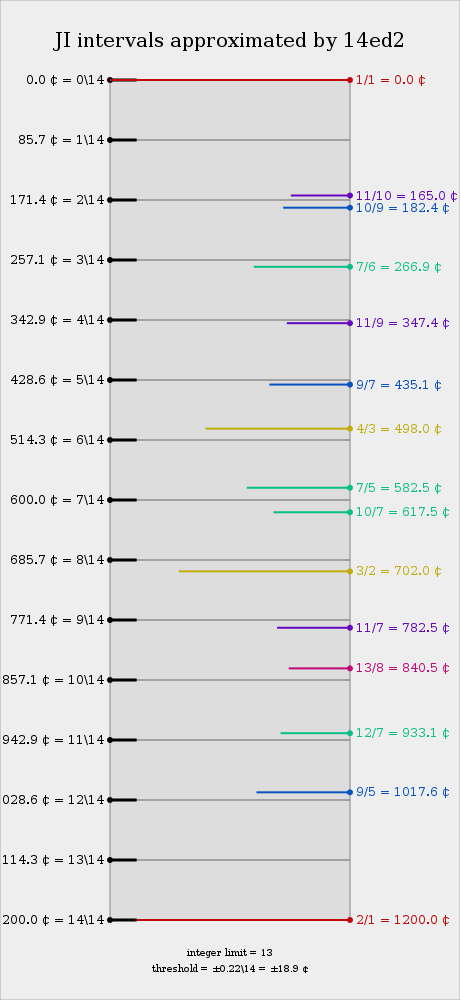
== Approximation to JI == | |||
=== Selected just intervals by error === | |||
==== Selected 13-limit intervals ==== | |||
[[File:14ed2-001.svg|alt=alt : Your browser has no SVG support.]] | |||
== Regular temperament properties == | |||
{| class="wikitable center-4 center-5 center-6" | |||
|- | |||
! rowspan="2" | [[Subgroup]] | |||
! rowspan="2" | [[Comma list]] | |||
! rowspan="2" | [[Mapping]] | |||
! rowspan="2" | Optimal<br>8ve stretch (¢) | |||
! colspan="2" | Tuning error | |||
|- | |||
! [[TE error|Absolute]] (¢) | |||
! [[TE simple badness|Relative]] (%) | |||
|- | |||
| 2.3.7 | |||
| 49/48, 2187/2048 | |||
| {{mapping| 14 22 39 }} | |||
| +6.52 | |||
| 4.64 | |||
| 5.38 | |||
|- | |||
| 2.3.7.11 | |||
| 33/32, 49/48, 243/242 | |||
| {{mapping| 14 22 39 48 }} | |||
| +7.58 | |||
| 4.42 | |||
| 5.12 | |||
|} | |||
=== Uniform maps === | |||
{{Uniform map|edo=14}} | |||
=== Rank-2 temperaments === | |||
* [[List of 14edo rank two temperaments by badness]] | |||
=== Commas === | |||
14et [[tempering out|tempers out]] the following [[comma]]s. This assumes the [[val]] {{val| 14 22 33 39 48 52 }}. | |||
{| class="commatable wikitable center-all left-3 right-4 left-6" | |||
|- | |||
! [[Harmonic limit|Prime<br>limit]] | |||
! [[Ratio]]<ref group="note">{{rd}}</ref> | |||
! [[Monzo]] | |||
! [[Cent]]s | |||
! [[Color name]] | |||
! Name | |||
|- | |||
| 3 | |||
| [[2187/2048]] | |||
| {{monzo| -11 7 }} | |||
| 113.69 | |||
| Lawa | |||
| Whitewood comma, apotome | |||
|- | |||
| 5 | |||
| [[27/25]] | |||
| {{monzo| 0 -3 2 }} | |||
| 133.24 | |||
| Gugu | |||
| Bug comma, large limma | |||
|- | |||
| 5 | |||
| [[2048/2025]] | |||
| {{monzo| 11 -4 -2 }} | |||
| 19.55 | |||
| Sagugu | |||
| Diaschisma | |||
|- | |||
|7 | |||
|[[21/20]] | |||
|[-2 1 -1 1⟩ | |||
|84.47 | |||
|Zogu | |||
|Chroma | |||
|- | |||
| 7 | |||
| [[36/35]] | |||
| {{monzo| 2 2 -1 -1 }} | |||
| 48.77 | |||
| Rugu | |||
| Mint comma, septimal quartertone | |||
|- | |||
| 7 | |||
| [[49/48]] | |||
| {{monzo| -4 -1 0 2 }} | |||
| 35.70 | |||
| Zozo | |||
| Sempahoresma, slendro diesis | |||
|- | |||
| 7 | |||
| [[1728/1715]] | |||
| {{monzo| 6 3 -1 -3 }} | |||
| 13.07 | |||
| Triru-agu | |||
| Orwellisma | |||
|- | |||
| 7 | |||
| [[10976/10935]] | |||
| {{monzo| 5 -7 -1 3 }} | |||
| 6.48 | |||
| Satrizo-agu | |||
| Hemimage comma | |||
|- | |||
| 7 | |||
| <abbr title="140737488355328/140710042265625">(30 digits)</abbr> | |||
| {{monzo| 47 -7 -7 -7 }} | |||
| 0.34 | |||
| Trisa-seprugu | |||
| [[Akjaysma]] | |||
|- | |||
| 11 | |||
| [[99/98]] | |||
| {{monzo| -1 2 0 -2 1 }} | |||
| 17.58 | |||
| Loruru | |||
| Mothwellsma | |||
|- | |||
| 11 | |||
| [[243/242]] | |||
| {{monzo| -1 5 0 0 -2 }} | |||
| 7.14 | |||
| Lulu | |||
| Rastma | |||
|- | |||
| 11 | |||
| [[385/384]] | |||
| {{monzo| -7 -1 1 1 1 }} | |||
| 4.50 | |||
| Lozoyo | |||
| Keenanisma | |||
|- | |||
| 13 | |||
| [[91/90]] | |||
| {{monzo| -1 -2 -1 1 0 1 }} | |||
| 19.13 | |||
| Thozogu | |||
| Superleap comma, biome comma | |||
|- | |||
| 13 | |||
| [[676/675]] | |||
| {{monzo| 2 -3 -2 0 0 2 }} | |||
| 2.56 | |||
| Bithogu | |||
| Island comma | |||
|} | |||
<references group="note" /> | |||
== Scales == | |||
=== MOS scales === | |||
{{Main|List of MOS scales in {{PAGENAME}}}} | |||
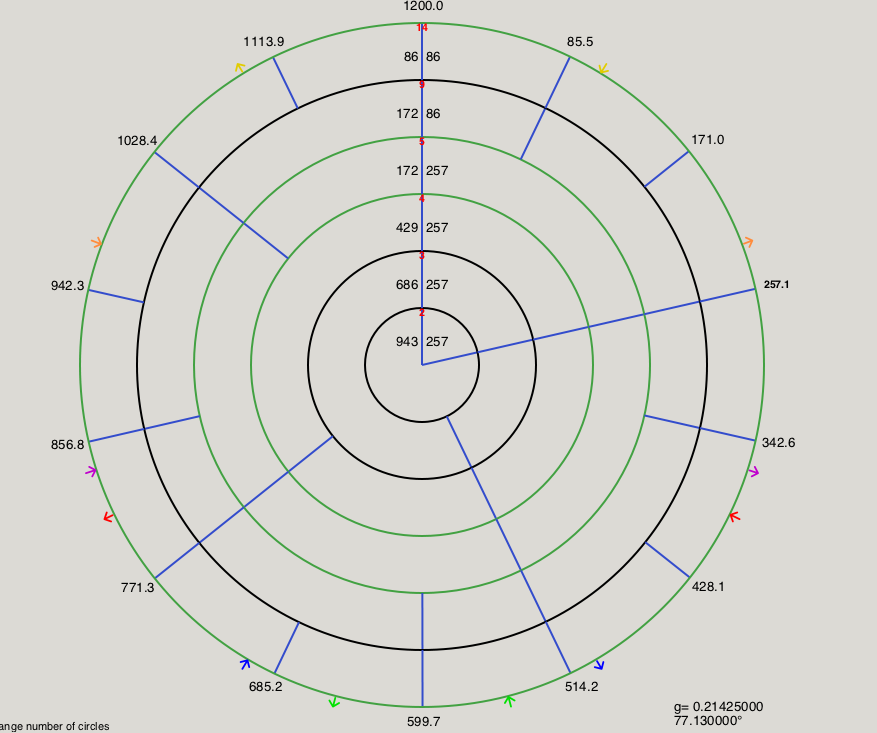
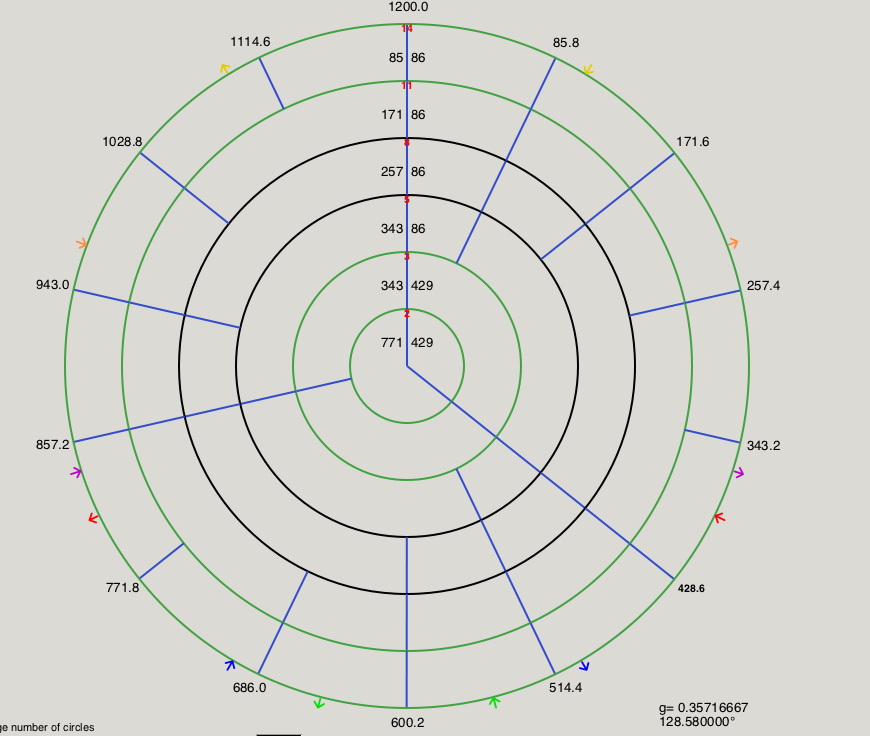
Here are the modes that create MOS scales in 14edo shown on horagrams from Scala, skipping multiples of 14: | |||
[[File:Screen Shot 2020-04-23 at 11.47.09 PM.png|none|thumb|877x877px|3\14 MOS using 1L 1s, 1L 2s, 1L 3s, 4L 1s, 5L 4s]] | |||
[[File:Screen Shot 2020-04-23 at 11.47.30 PM.png|none|thumb|870x870px|5\14 MOS using 1L 1s, 2L 1s, 3L 2s, 3L 5s, 3L 8s]] | |||
==== Beep[9] ==== | |||
14edo is also the largest edo whose patent val [[support]]s [[beep]] temperament, tempering out the chromatic semitone (21:20), and falling toward the "brittle" (fifths wider than in 9edo) end of that spectrum. beep is one of the simplest 7-limit temperaments, although rather inaccurate (the 7:5 is mapped onto 6\14, over 70 cents flat). Its otonal/major and utonal/minor tetrads are inversions of one another, which allows a greater variety of chord progressions (since different inversions of the same chord may have very different expressive qualities). Despite being so heavily tempered, the tetrads are still recognizable and aren't unpleasant-sounding as long as one uses the right timbres ("bell-like" or opaque-sounding ones probably work best). beep forms enneatonic modes which are melodically strong and are very similar to diatonic modes, only with two mediants and submediants instead of one. Beep[9] has similarities to mavila, slendro, and pelog scales as well. | |||
Using beep[9], we could name the intervals of 14edo as follows. The 3, 5, 6, 8, 9, and 11-step intervals are all consonant, while 1, 2, 4, 7, 10, 12, and 13 steps are dissonant. There is no distinction between "perfect" (modulatory) and "imperfect" (major/minor) consonances here; there are enough chords here that root motion may occur by ''any'' consonant interval, and thus ''all'' six consonances are "perfect" intervals, rather than just two of them as in the diatonic system. As in the diatonic scale, the perfect intervals come in pairs separated by a major second, and with a characteristic dissonance between them; in beep[9] there are three such pairs rather than just one. | |||
* 1\14: Minor 2nd<sub>9</sub>: functions similarly to the diatonic minor second, but is more incisive. | |||
* 2\14: Major 2nd<sub>9</sub>: functions similarly to the diatonic major second, but is narrower and has a rather different quality. | |||
* 3\14: Perfect 3rd<sub>9</sub>: the generator, standing in for 8:7, 7:6, ''and'' 6:5, but closest to 7:6. | |||
* 4\14: Augmented 3rd<sub>9</sub>, diminished 4th<sub>9</sub>: A dissonance, falling in between two perfect consonances and hence analogous to the tritone. | |||
* 5\14: Perfect 4th<sub>9</sub>: technically represents 5:4 but is quite a bit wider. | |||
* 6\14: Perfect 5th<sub>9</sub>: represents 4:3 and 7:5, much closer to the former. | |||
* 7\14: Augmented 5th<sub>9</sub>, diminished 6th<sub>9</sub>: The so-called "tritone" (but no longer made up of three whole tones). Like 4\14 and 10\14, this is a characteristic dissonance separating a pair of perfect consonances. | |||
* 8\14: Perfect 6th<sub>9</sub>: represents 10:7 and 3:2, much closer to the latter. | |||
* 9\14: Perfect 7th<sub>9</sub>: technically represents 8:5 but noticeably narrower. | |||
* 10\14: Augmented 7th<sub>9</sub>, diminished 8th<sub>9</sub>: The third and final characteristic dissonance, analogous to the tritone. | |||
* 11\14: Perfect 8th<sub>9</sub>: Represents 5:3, 12:7 and 7:4. | |||
* 12\14: Minor 9th<sub>9</sub>: Analogous to the diatonic minor seventh, but sharper than usual. | |||
* 13\14: Major 9th<sub>9</sub>: A high, incisive leading tone. | |||
* 14\14: The 10th<sub>9</sub> or "enneatonic decave" (i. e. the octave, 2:1). | |||
=== Others === | |||
* 2 2 2 2 2 2 2 - [[Equiheptatonic]] (exactly [[7edo]]) | |||
* 2 2 2 2 1 4 1 - Fennec{{idiosyncratic}} (original/default tuning) | |||
* 1 4 1 2 2 2 2 - Inverse fennec{{idiosyncratic}} (original/default tuning) | |||
* 3 1 4 1 4 1 - Pseudo-[[augmented]] | |||
* 1 4 1 2 1 4 1 - Pseudo-double harmonic minor | |||
== Diagrams == | |||
[[File:14edo_wheel.png|alt=14edo wheel.png|343x343px|14edo wheel.png]] | |||
== Software support == | |||
[[File:SA14 for Mus2.zip]] | |||
[[File:14edo_mus2.jpg|thumb]] | |||
== Music == | |||
{{Main|Music in 14edo}} | |||
{{Catrel|14edo tracks}} | |||
== See also == | |||
* [[Lumatone mapping for 14edo]] | |||
* [[MisterShafXen’s take on 14edo harmony]] | |||
== Further reading == | |||
[[File:Libro_Tetradecafónico.PNG|alt=Libro_Tetradecafónico.PNG|Libro_Tetradecafónico.PNG|thumb|''Tetradecaphonic Scales for Guitar'' cover art.]] | |||
* [[Sword, Ron]]. ''[http://www.metatonalmusic.com/books.html Tetradecaphonic Scales for Guitar: Scales, Chord-Scales, Notation, and Theory for Fourteen Equal Divisions of the Octave]''. 2009. | |||
[[Category:14edo| ]] <!-- main article --> | |||
[[Category:Equal divisions of the octave|##]] <!-- 2-digit number --> | |||
[[Category:Modes]] | |||
[[Category:Teentuning]] | |||
Latest revision as of 01:07, 20 August 2025
| ← 13edo | 14edo | 15edo → |
14 equal divisions of the octave (abbreviated 14edo or 14ed2), also called 14-tone equal temperament (14tet) or 14 equal temperament (14et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 14 equal parts of about 85.7 ¢ each. Each step represents a frequency ratio of 21/14, or the 14th root of 2.
Theory
The character of 14edo does not well serve those seeking low-limit JI approaches, with the exception of 5:7:9:11:17:19 (which is quite well approximated, relative to other JI approximations of the low-numbered edos). However, the ratios 7/5, 7/6, 9/7, 10/7, 10/9, 11/7, 11/9, and 11/10 are all recognizably approximated, and if you accept that 14edo offers approximations of these intervals, you end up with a low-complexity, high-damage 11-limit temperament where the commas listed later in this page are tempered out. This leads to some of the bizarre equivalences described in the second "Approximate ratios" column in the table.
14et has quite a bit of xenharmonic appeal, in a similar way to 17et, on account of having three types of 3rd and three types of 6th, rather than the usual two of 12et. Since 14et also has a recognizable 4th and 5th, this makes it good for those wishing to explore alternative triadic harmonies without adding significantly more notes. It possesses a triad-rich 9-note mos scale of 5L 4s, wherein 7 of 9 notes are tonic to a subminor, supermajor, and/or neutral triad.
14edo contains an omnidiatonic scale that can replace the standard diatonic scale, allowing for recognizable triadic harmony using the chords 6:7:9 and 14:18:21, as well as a neutral chord which can be seen as 2:sqrt(6):3.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | -16.2 | +42.3 | -26.0 | -37.0 | +16.6 | -19.2 | -40.4 | -28.3 | -1.0 | -30.7 |
| Relative (%) | +0.0 | -18.9 | +49.3 | -30.3 | -43.2 | +19.4 | -22.4 | -47.1 | -33.0 | -1.2 | -35.9 | |
| Steps (reduced) |
14 (0) |
22 (8) |
33 (5) |
39 (11) |
48 (6) |
52 (10) |
57 (1) |
59 (3) |
63 (7) |
68 (12) |
69 (13) | |
Octave stretch
14edo benefits from octave stretch as harmonics 3, 7, and 11 are all tuned flat. 22edt, 36ed6 and 42zpi are among the possible choices.
Subsets and supersets
Since 14 factors into primes as 2 × 7, 14edo contains 2edo and 7edo as subsets.
Notation
Ups and downs notation
| Steps | Cents | Approximate Harmonics |
Approximate Ratios 1 [note 1] |
Approximate Ratios 2 [note 2] |
Approximate Ratios 3 [note 3] |
Ups and downs notation | Interval Type | Audio | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.000 | 1 | 1/1 | 1/1 | 1/1 | unison | 1 | D | Unison | |
| 1 | 85.714 | 67 | 20/19, 19/18, 18/17 | 28/27, 22/21, 21/20 | up-unison, down-2nd |
^1, v2 | ^D, vE | Narrow Minor 2nd | ||
| 2 | 171.429 | 71 | 11/10, 10/9, 19/17 | 12/11, 11/10, 10/9, 9/8 | 11/10, 10/9 | 2nd | 2 | E | Neutral 2nd | |
| 3 | 257.143 | 37 | 22/19, 20/17 | 8/7, 7/6 | 15/13, 7/6 | up-2nd, down-3rd |
^2, v3 | ^E, vF | Subminor 3rd | |
| 4 | 342.857 | 39 | 17/14, 11/9 | 6/5, 11/9, 5/4 | 11/9 | 3rd | 3 | F | Neutral 3rd | |
| 5 | 428.571 | 41 | 22/17, 14/11, 9/7 | 14/11, 9/7 | 14/11, 9/7 | up-3rd, down-4th |
^3, v4 | ^F, vG | Supermajor 3rd | |
| 6 | 514.286 | 43 | 19/14 | 4/3, 15/11, 11/8 | 4/3 | 4th | 4 | G | Wide 4th | |
| 7 | 600.000 | 91 | 7/5, 10/7 | 7/5, 10/7 | 7/5, 10/7 | up-4th, down-5th |
^4, v5 | ^G, vA | Tritone | |
| 8 | 685.714 | 95 | 28/19 | 16/11, 22/15, 3/2 | 3/2 | 5th | 5 | A | Narrow 5th | |
| 9 | 771.429 | 25 | 14/9, 11/7, 17/11 | 14/9, 11/7 | 14/9, 11/7 | up-5th, down-6th |
^5, v6 | ^A, vB | Subminor 6th | |
| 10 | 857.143 | 105 | 18/11, 28/17 | 8/5, 18/11, 5/3 | 18/11 | 6th | 6 | B | Neutral 6th | |
| 11 | 942.857 | 55 | 17/10, 19/11 | 12/7, 7/4 | 12/7, 26/15 | up-6th, down-7th |
^6, v7 | ^B, vC | Supermajor 6th | |
| 12 | 1028.571 | 29 | 19/34, 9/5, 20/11 | 16/9, 9/5, 20/11, 11/6 | 9/5, 20/11 | 7th | 7 | C | Neutral 7th | |
| 13 | 1114.286 | 61 | 17/9, 36/19, 19/10 | 40/21, 21/11, 27/14 | up-7th, down-8ve |
^7, v8 | ^C, vD | Wide Major 7th | ||
| 14 | 1200.000 | 2 | 2/1 | 2/1 | 2/1 | 8ve | 8 | D | Octave | |
- ↑ Based on treating 14edo as a 2.7/5.9/5.11/5.17/5.19/5 subgroup temperament; other approaches are also possible.
- ↑ Based on treating 14edo as an 11-limit temperament of ⟨14 22 32 39 48] (14c).
- ↑ Nearest 15-odd-limit intervals by direct approximation.
Sagittal notation
This notation uses the same sagittal sequence as 9-EDO, is a subset of the notations for EDOs 28 and 42b, and is a superset of the notation for 7-EDO.

Ivor Darreg's notation
Ivor Darreg wrote in this article:
The 14-tone scale presents a new situation: while one might use ordinary sharps and flats in addition to conventional naturals for the notes of the 7-tone-equal temperament, it would be misleading and confusing to do so, because there is a 7-tone circle of fifths (admittedly quite distorted) already notatable and nameable as F C G D A E B in the usual manner. But there is no 14-tone circle of fifths. There is simply a second set of 7 fifths in a circle which does not intersect the with the first set. Thus is we think of B-flat and B, or B-natural and F-sharp, the 14-tone-system interval would NOT be a fifth of that system and would not sound like one, since B F would be the very same kind of distorted fifth that C G or A E happens to be in 7 or 14. Our suggestion is to call the new notes of 14, the second set of 7, F* C* G* D* A* E* B*, and use asterisks or arrows or whatever you please on the staff. Or just number the tones as for 13.
The following chart (made by TDW) shows this recommendation as "standard notation" as well as a proposed alternative.
|
| Intervallic Cycle of 14 steps Equal per Octave |
Chord names
Ups and downs can be used to name 14edo chords. Because every interval is perfect, the quality can be omitted, and the words major, minor, augmented and diminished are never used. Alterations are always enclosed in parentheses, additions never are. An up or down immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13).
0-4-8 = C E G = C = C or C perfect
0-3-8 = C vE G = Cv = C down
0-5-8 = C ^E G = C^ = C up
0-4-7 = C E vG = C(v5) = C down-five
0-5-9 = C ^E ^G = C^(^5) = C up up-five
0-4-8-12 = C E G B = C7 = C seven
0-4-8-11 = C E G vB = C,v7 = C add down-seven
0-3-8-12 = C vE G B = Cv,7 = C down add seven
0-3-8-11 = C vE G vB = Cv7 = C down-seven
For a more complete list, see Ups and downs notation #Chords and Chord Progressions.
Approximation to JI
Selected just intervals by error
Selected 13-limit intervals
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3.7 | 49/48, 2187/2048 | [⟨14 22 39]] | +6.52 | 4.64 | 5.38 |
| 2.3.7.11 | 33/32, 49/48, 243/242 | [⟨14 22 39 48]] | +7.58 | 4.42 | 5.12 |
Uniform maps
| Min. size | Max. size | Wart notation | Map |
|---|---|---|---|
| 13.7306 | 13.9173 | 14cf | ⟨14 22 32 39 48 51] |
| 13.9173 | 13.9970 | 14c | ⟨14 22 32 39 48 52] |
| 13.9970 | 14.0196 | 14 | ⟨14 22 33 39 48 52] |
| 14.0196 | 14.0702 | 14e | ⟨14 22 33 39 49 52] |
| 14.0702 | 14.1875 | 14de | ⟨14 22 33 40 49 52] |
| 14.1875 | 14.1959 | 14deff | ⟨14 22 33 40 49 53] |
| 14.1959 | 14.3087 | 14bdeff | ⟨14 23 33 40 49 53] |
Rank-2 temperaments
Commas
14et tempers out the following commas. This assumes the val ⟨14 22 33 39 48 52].
| Prime limit |
Ratio[note 1] | Monzo | Cents | Color name | Name |
|---|---|---|---|---|---|
| 3 | 2187/2048 | [-11 7⟩ | 113.69 | Lawa | Whitewood comma, apotome |
| 5 | 27/25 | [0 -3 2⟩ | 133.24 | Gugu | Bug comma, large limma |
| 5 | 2048/2025 | [11 -4 -2⟩ | 19.55 | Sagugu | Diaschisma |
| 7 | 21/20 | [-2 1 -1 1⟩ | 84.47 | Zogu | Chroma |
| 7 | 36/35 | [2 2 -1 -1⟩ | 48.77 | Rugu | Mint comma, septimal quartertone |
| 7 | 49/48 | [-4 -1 0 2⟩ | 35.70 | Zozo | Sempahoresma, slendro diesis |
| 7 | 1728/1715 | [6 3 -1 -3⟩ | 13.07 | Triru-agu | Orwellisma |
| 7 | 10976/10935 | [5 -7 -1 3⟩ | 6.48 | Satrizo-agu | Hemimage comma |
| 7 | (30 digits) | [47 -7 -7 -7⟩ | 0.34 | Trisa-seprugu | Akjaysma |
| 11 | 99/98 | [-1 2 0 -2 1⟩ | 17.58 | Loruru | Mothwellsma |
| 11 | 243/242 | [-1 5 0 0 -2⟩ | 7.14 | Lulu | Rastma |
| 11 | 385/384 | [-7 -1 1 1 1⟩ | 4.50 | Lozoyo | Keenanisma |
| 13 | 91/90 | [-1 -2 -1 1 0 1⟩ | 19.13 | Thozogu | Superleap comma, biome comma |
| 13 | 676/675 | [2 -3 -2 0 0 2⟩ | 2.56 | Bithogu | Island comma |
- ↑ Ratios longer than 10 digits are presented by placeholders with informative hints.
Scales
MOS scales
Here are the modes that create MOS scales in 14edo shown on horagrams from Scala, skipping multiples of 14:
Beep[9]
14edo is also the largest edo whose patent val supports beep temperament, tempering out the chromatic semitone (21:20), and falling toward the "brittle" (fifths wider than in 9edo) end of that spectrum. beep is one of the simplest 7-limit temperaments, although rather inaccurate (the 7:5 is mapped onto 6\14, over 70 cents flat). Its otonal/major and utonal/minor tetrads are inversions of one another, which allows a greater variety of chord progressions (since different inversions of the same chord may have very different expressive qualities). Despite being so heavily tempered, the tetrads are still recognizable and aren't unpleasant-sounding as long as one uses the right timbres ("bell-like" or opaque-sounding ones probably work best). beep forms enneatonic modes which are melodically strong and are very similar to diatonic modes, only with two mediants and submediants instead of one. Beep[9] has similarities to mavila, slendro, and pelog scales as well.
Using beep[9], we could name the intervals of 14edo as follows. The 3, 5, 6, 8, 9, and 11-step intervals are all consonant, while 1, 2, 4, 7, 10, 12, and 13 steps are dissonant. There is no distinction between "perfect" (modulatory) and "imperfect" (major/minor) consonances here; there are enough chords here that root motion may occur by any consonant interval, and thus all six consonances are "perfect" intervals, rather than just two of them as in the diatonic system. As in the diatonic scale, the perfect intervals come in pairs separated by a major second, and with a characteristic dissonance between them; in beep[9] there are three such pairs rather than just one.
- 1\14: Minor 2nd9: functions similarly to the diatonic minor second, but is more incisive.
- 2\14: Major 2nd9: functions similarly to the diatonic major second, but is narrower and has a rather different quality.
- 3\14: Perfect 3rd9: the generator, standing in for 8:7, 7:6, and 6:5, but closest to 7:6.
- 4\14: Augmented 3rd9, diminished 4th9: A dissonance, falling in between two perfect consonances and hence analogous to the tritone.
- 5\14: Perfect 4th9: technically represents 5:4 but is quite a bit wider.
- 6\14: Perfect 5th9: represents 4:3 and 7:5, much closer to the former.
- 7\14: Augmented 5th9, diminished 6th9: The so-called "tritone" (but no longer made up of three whole tones). Like 4\14 and 10\14, this is a characteristic dissonance separating a pair of perfect consonances.
- 8\14: Perfect 6th9: represents 10:7 and 3:2, much closer to the latter.
- 9\14: Perfect 7th9: technically represents 8:5 but noticeably narrower.
- 10\14: Augmented 7th9, diminished 8th9: The third and final characteristic dissonance, analogous to the tritone.
- 11\14: Perfect 8th9: Represents 5:3, 12:7 and 7:4.
- 12\14: Minor 9th9: Analogous to the diatonic minor seventh, but sharper than usual.
- 13\14: Major 9th9: A high, incisive leading tone.
- 14\14: The 10th9 or "enneatonic decave" (i. e. the octave, 2:1).
Others
- 2 2 2 2 2 2 2 - Equiheptatonic (exactly 7edo)
- 2 2 2 2 1 4 1 - Fennec[idiosyncratic term] (original/default tuning)
- 1 4 1 2 2 2 2 - Inverse fennec[idiosyncratic term] (original/default tuning)
- 3 1 4 1 4 1 - Pseudo-augmented
- 1 4 1 2 1 4 1 - Pseudo-double harmonic minor
Diagrams
Software support

Music
- See also: Category:14edo tracks
See also
Further reading