Orwell: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
Inthar (talk | contribs)
autopatrolled, emailconfirmed
15,004 edits
m →Interval chain: bolded harmonics
m Undo revision 198110 by ArrowHead294 (talk)
Tag: Undo
 
(63 intermediate revisions by 13 users not shown)
Line 1: Line 1:
{{interwiki
| de = Orwell
| en = Orwell
| es =
| ja =
}}
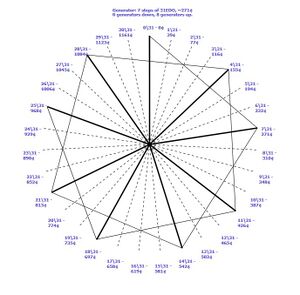
[[File:Orwell generator in 31.jpg|thumb|Martin Aurell's diagram showing Orwell[9] generated in 31 tone equal temperament.]]
[[File:Orwell generator in 31.jpg|thumb|Martin Aurell's diagram showing Orwell[9] generated in 31 tone equal temperament.]]
<span style="display: block; text-align: right;">[[de:Orwell|de:Orwell]]</span>
__FORCETOC__
=Properties=
[[Semicomma_family#Seven limit children-Orwell|Orwell]] — so named because 19 steps of [[84edo|84edo]], or 19\84, is a possible generator — is an excellent 7-limit temperament and an amazing (because of the low complexity of 11) 11-limit temperament. The "perfect twelfth" 3/1 is divided into 7 equal steps. One of these steps represents 7/6; three represent 8/5. It's a member of the [[Semicomma_family|Semicomma family]]. Alternately, the "fifth harmonic" 5/1 divided into 3 equal steps also makes a good orwell generator, being ~12/7.


In the 11 limit, two generators are equated to 11/8 (meaning 99/98 is tempered out). This means that three stacked generators makes the [[orwell_tetrad|orwell tetrad]] 1/1-7/6-11/8-8/5, a chord in which every interval is a (tempered) 11-limit consonance. Other such chords in orwell are the [[keenanismic_chords|keenanismic tetrads]] and the [[swetismic_chords|swetismic chords]].
'''Orwell''' – so named because 19 steps of [[84edo]], i.e. 19\84, is a possible generator – is an excellent [[7-limit]] [[regular temperament|temperament]] and an amazing [[11-limit]] temperament because of the simplicity of [[harmonic]] [[11/1|11]].


Compatible equal temperaments include [[22edo|22edo]], [[31edo|31edo]], [[53edo|53edo]], and [[84edo|84edo]]. Orwell is in better tune in lower limits than higher ones; the [[Optimal_patent_val|optimal patent val]] is [[296edo|296edo]] in the 5-limit, [[137edo|137edo]] in the 7-limit, and [[53edo|53edo]] in the 11-limit. It tempers out the semicomma in the 5-limit, and so belongs to the [[Semicomma_family|semicomma family]]. In the 7-limit it tempers out 225/224, 1728/1715, 2430/2401 and 6144/6125 in the 7-limit, and 99/98, 121/120, 176/175, 385/384 and 540/539 in the 11-limit. By adding 275/273 to the list of commas it can be extended to the 13-limit as [[Semicomma_family#Orwell-13-limit|tridecimal orwell]], and by adding instead 66/65, [[Semicomma_family#Winston|winston temperament]].
In orwell, the [[3/1|just perfect twelfth (3/1)]] is divided into 7 equal steps. One of these steps represents [[7/6]]; three represent [[8/5]]. Alternately, the [[5/1|5th harmonic (5/1)]] divided into 3 equal steps also makes a good orwell generator, being [[~]][[12/7]].


===Watcher===
In the 11-limit, two generators are equated to [[11/8]] (meaning [[99/98]] is tempered out). This means that three stacked generators makes the [[orwell tetrad]] 1–7/6–11/8–8/5, a chord in which every interval is a (tempered) 11-odd-limit consonance. Other such chords in orwell are the [[keenanismic chords]] and the [[swetismic chords]].


By switching the roles of the period and generator, we end up with a nonoctave temperament that is to orwell what [[Angel|angel]] and [[devadoot|devadoot]] are to meantone and magic, respectively. There is an interesting MOS with 7 notes per period; if this is derived as a subset of [[84edt|84edt]] (which has 12 notes per period, and is almost identical to 53edo), the resulting MOS has the same structure as the 12edo diatonic scale, only compressed so that the period is ~272 cents rather than an octave! Thus, a piano keyboard for this MOS would look exactly the same as a typical keyboard, only what looks like an octave wouldn't be one anymore. This temperament could be called [https://en.wikipedia.org/wiki/Watcher_(angel) watcher], a reference to a class of angels whose very name carries Orwellian connotations. The 12-limit otonality (1:2:3:4:5:6:7:8:9:10:11:12) and utonality both have complexity 4. If we consider these to be the fundamental consonances, then using the 7-note-per period MOS, there are exactly 3 of each type per period, which again is analogous to the diatonic scale. While angel and devadoot don't perform well past the 10-limit, watcher handles the 12-limit with ease. Straight-fretted watcher guitars could be built as long as the strings were all tuned to period-equivalent notes.
Compatible equal temperaments include [[22edo]], [[31edo]], [[53edo]], and [[84edo]]. Orwell is in better tune in lower limits than higher ones; the [[optimal patent val]] is [[296edo]] in the 5-limit, [[137edo]] in the 7-limit, and [[53edo]] in the 11-limit. It tempers out the semicomma in the 5-limit, and so belongs to the [[semicomma family]]. In the 7-limit it tempers out [[225/224]], [[1728/1715]], [[2430/2401]] and [[6144/6125]], and in the 11-limit, 99/98, [[121/120]], [[176/175]], [[385/384]] and [[540/539]]. By adding [[275/273]] to the list of commas it can be extended to the 13-limit as [[Semicomma family #Orwell|tridecimal orwell]], and by adding instead [[66/65]], [[Semicomma family #Winston|winston temperament]]. See [[Orwell extensions]] for details about 13-limit extensions.  


=Interval chain=
See [[Semicomma family #Orwell]] for technical details.


{| class="wikitable"
== Interval chain ==
Odd harmonics 1–21 and their inverses are in '''bold'''.
{| class="wikitable center-1 right-2"
|-
|-
! | Generators
! #
! | Cents*
! Cents*
! | 11-limit ratios
! Approximate ratios
 
(orwell mapping)
! | 13-limit ratios
 
(orwell mapping)
! | 13-limit ratios
 
(winston mapping)
! | 13-limit ratios
 
(blair mapping)
|-
|-
| | 0
| 0
| style="text-align:right;" | 0.00
| 0.00
| | 1/1
| '''1/1'''
| |
| |
| |
|-
|-
| | 1
| 1
| style="text-align:right;" | 271.43
| 271.46
| | 7/6
| 7/6
| |
| |
| | 13/11, 15/13
|-
|-
| | 2
| 2
| style="text-align:right;" | 542.85
| 542.91
| | ''11/8''', 15/11
| '''11/8''', 15/11
| |
| | 18/13
| | 35/26, 39/28
|-
|-
| | 3
| 3
| style="text-align:right;" | 814.28
| 814.37
| | '''8/5'''
| '''8/5'''
| |
| | 21/13, 52/33
| | '''13/8'''
|-
|-
| | 4
| 4
| style="text-align:right;" | 1085.71
| 1085.82
| | '''15/8''', 28/15
| '''15/8''', 28/15
| |
| | 13/7
| | 24/13
|-
|-
| | 5
| 5
| style="text-align:right;" | 157.13
| 157.28
| | 12/11, 11/10, 35/32
| 11/10, 12/11, 35/32
| |
| | 13/12
| | 14/13
|-
|-
| | 6
| 6
| style="text-align:right;" | 428.56
| 428.73
| | 14/11, 9/7, 32/25
| 9/7, 14/11, 32/25
| |
| |
| | 13/10, 33/26
|-
|-
| | 7
| 7
| style="text-align:right;" | 699.98
| 700.19
| | '''3/2'''
| '''3/2'''
| |
| | 52/35
| |
|-
|-
| | 8
| 8
| style="text-align:right;" | 971.41
| 971.64
| | '''7/4'''
| '''7/4'''
| |
| | 26/15
| |
|-
|-
| | 9
| 9
| style="text-align:right;" | 42.84
| 43.10
| | 49/48, 36/35, 33/32
| 33/32, 36/35, 49/48
| | 40/39
| | 27/26
| | 26/25
|-
|-
| | 10
| 10
| style="text-align:right;" | 314.26
| 314.55
| | 6/5
| 6/5
| |
| | 13/11
| | 39/32
|-
|-
| | 11
| 11
| style="text-align:right;" | 585.69
| 586.01
| | 7/5
| 7/5
| |
| | 39/28
| | 18/13
|-
|-
| | 12
| 12
| style="text-align:right;" | 857.12
| 857.46
| | 18/11
| 18/11
| | 64/39
| | 13/8
| | 21/13
|-
|-
| | 13
| 13
| style="text-align:right;" | 1128.54
| 1128.92
| | 21/11, 27/14, 48/25
| 21/11, 27/14, 48/25
| | 25/13
| |
| | 39/20
|-
|-
| | 14
| 14
| style="text-align:right;" | 199.97
| 200.37
| | '''9/8''', 28/25
| '''9/8''', 28/25
| |
| |
| |
|-
|-
| | 15
| 15
| style="text-align:right;" | 471.40
| 471.83
| | '''21/16'''
| '''21/16'''
| |
| | 13/10
| |
|-
|-
| | 16
| 16
| style="text-align:right;" | 742.82
| 743.28
| | 49/32, 54/35
| 49/32, 54/35
| | 20/13
| |
| |
|-
|-
| | 17
| 17
| style="text-align:right;" | 1014.25
| 1014.74
| | 9/5
| 9/5
| |
| |
| |
|-
|-
| | 18
| 18
| style="text-align:right;" | 85.67
| 86.19
| | 21/20
| 21/20
| |
| | 26/25
| | 27/26
|-
|-
| | 19
| 19
| style="text-align:right;" | 357.10
| 357.65
| | 27/22, 49/40
| 27/22, 49/40
| | 16/13
| | 39/32
| |
|-
|-
| | 20
| 20
| style="text-align:right;" | 628.52
| 629.10
| | 36/25
| 36/25
| | 56/39
| |
| |
|-
|-
| | 21
| 21
| style="text-align:right;" | 899.95
| 900.56
| | 27/16, 42/25
| 27/16, 42/25
| | 22/13
| |
| |
|-
|-
| | 22
| 22
| style="text-align:right;" | 1171.38
| 1172.01
| | 63/32
| 63/32
| |
| | 39/20
| |
|}
|}
*in 11-limit POTE tuning
<nowiki/>* In 11-limit CWE tuning, octave reduced


=Spectrum of Orwell Tunings by Eigenmonzos=
== Chords and harmony ==
{{Main| Chords of orwell }}
{{See also| Functional harmony in rank-2 temperaments }}


{| class="wikitable"
The fundamental otonal consonance of orwell, voiced in a roughly {{w|tertian harmony|tertian}} manner, is 4:5:6:7:9:11. In terms of generator steps this is 0–(−3)–7–8–14–2, only available in a 22-tone mos. However, some subsets of this chord are way simpler, such as 8:11:12:14, which is 1–11/8–3/2–7/4 (0–2–7–8).
 
The generator, ~7/6, is a septimal interval, so chords could instead be built around it as 1–7/6–3/2 (0–1–7), 1–7/4–3 (0–8–7), or tetrads such as 1–7/6–3/2–7/4 (0–1–7–8).
 
To 1–7/6–3/2–7/4 we may add 11/8, or to 1–11/8–3/2–7/4 we may add 7/6, to form an essentially tempered pentad, 1–7/6–11/8–3/2–7/4 (0–1–2–7–8). Its inverse is 1–12/11–9/7–3/2–12/7 (0–5–6–7–(−1)), which can serve as a minor counterpart. This is similar, but also in clear contrast to the 1–5/4–3/2 (0–4–1) and 1–6/5–3/2 (0–(−3)–1) chords of [[meantone]]. Two approaches to functional harmony thus arise.
 
First, we can treat the septimal chords above as the basis of harmony, but swapping the roles of 3 and 7 according to their temperamental complexities (number of generator steps). Thus a "dominant" chord is either 7/6 or 12/7 over tonic; a "subdominant" chord is either 7/6 or 12/7 under tonic. This leads to an approach closely adherent to mos scales. The 9-tone mos contains a tonic and a "dominant" triad. The 13-tone mos is good for encapsulating tonic, "pre-dominant", and "dominant" functions, triads to pentads alike.
 
Second, we can treat the same chords as the basis of harmony, and keeping the role of the [[chain of fifths]] as the spine on which the functions are defined. This means dominant is still 3/2 over tonic, for example. A consequence is we must step out of the logic of mos scales, as they are often too restrictive without the many fifths to stack. This is essentially working in JI, but using the commas tempered out in some way to lock into the identity of the temperament.
 
== Scales ==
{{Main| Orwell scales }}
 
=== Mos scales ===
* [[Orwell5]]
 
; 9-tone scales (sLsLsLsLs, proper)
* [[Orwell9]] – 84edo tuning
* [[Orwell9-12]] – 7-limit POTE tuning, mapped to 12-tones
 
[[file:OrwellNonatonicPOTE.mp3]] in POTE tuning
 
[[file:OrwellNonatonic22edo.mp3]] in 22edo
 
[[file:OrwellNonatonic53edo.mp3]] in 53edo
 
{| class="wikitable center-all"
|-
|-
! | Eigenmonzo
! Small ("minor") interval
! | Subminor Third
| 114.29
| 228.59
| 385.72
| 500.02
| 657.15
| 771.44
| 928.57
| 1042.87
|-
|-
| | 7/6
! JI intervals represented
| | 266.871
| 15/14~16/15
| 8/7
| 5/4
| 4/3
| 16/11
| 14/9~11/7
| 12/7
| 11/6
|-
|-
| | 14/11
! Large ("major") interval
| | 269.585
| 157.13
| 271.43
| 428.56
| 542.85
| 699.98
| 814.28
| 971.41
| 1085.71
|-
|-
| | 12/11
! JI intervals represented
| | 270.127
| 12/11~11/10
| 7/6
| 14/11~9/7
| 11/8
| 3/2
| 8/5
| 7/4
| 15/8
|}
 
; 13-tone scales (LsLLsLLLsLLsL, improper)
* [[Orwell13]] – 84edo tuning
* [[Orwellwoo13]] – [6 5/2] unchanged-interval (eigenmonzo) tuning
 
{| class="wikitable center-all"
|-
|-
| | 11/9
! Small ("minor") interval
| | 271.049
| 42.84
| 157.13
| 271.43
| 314.26
| 428.56
| 542.85
| 585.69
| 699.98
| 814.28
| 857
| 971.41
| 1085.71
|-
|-
| | 8/7
! JI intervals represented
| | 271.103
|
| 12/11~11/10
| 7/6
| 6/5
| 14/11~9/7
| 11/8
| 7/5
| 3/2
| 8/5
| 18/11
| 7/4
| 15/8
|-
|-
| | 7/5
! Large ("major") interval
| | 271.137 (7 and 11 limit minimx)
| 114.29
| 228.59
| 342.88
| 385.72
| 500.02
| 614.31
| 657.15
| 771.44
| 885.74
| 928.57
| 1042.87
| 1157.16
|-
|-
| | 5/4
! JI intervals represented
| | 271.229
| 15/14~16/15
|-
| 8/7
| | 6/5
| 11/9
| | 271.564 (5 limit minimax)
| 5/4
| 4/3
| 10/7
| 16/11
| 14/9~11/7
| 5/3
| 12/7
| 11/6
|  
|}
 
; 22-tone scales
* [[Orwell22]]
* [[Orwellwoo22]] – [6 5/2] unchanged-interval (eigenmonzo) tuning
 
=== Transversal scales ===
* [[Orwell13trans]]
* [[Orwell13trans57]]
* [[Orwell22trans]]
* [[Orwell22trans57]]
* [[Orwell31trans]]
* [[Orwell31trans57]]
 
=== Others ===
* [[Orwell-graham]] – 13-tone modmos in 53edo tuning
* [[Orwell13-modmos-containing-minerva12]] – 13-tone modmos in POTE tuning
* [[Minerva12-orwell-tempered]] – Minerva[12] tempered to orwell
 
== Tunings ==
{| class="wikitable mw-collapsible mw-collapsed"
|+ style="font-size: 105%; white-space: nowrap;" | 7-limit prime-optimized tunings
|-
|-
| | 10/9
! rowspan="2" |  
| | 271.623 (9 limit minimax)
! colspan="2" | Euclidean
|-
|-
| | 4/3
! Constrained
| | 271.708
! Constrained & skewed
|-
|-
| | 9/7
! Equilateral
| | 272.514
| CEE: ~7/6 = 271.3553{{c}}
| CSEE: ~7/6 = 271.3339{{c}}
|-
|-
| | 11/10
! Tenney
| | 273.001
| CTE: ~7/6 = 271.5130{{c}}
| CWE: ~7/6 = 271.5097{{c}}
|-
|-
| | 11/8
! Benedetti, <br>Wilson
| | 275.659
| CBE: ~7/6 = 271.5725{{c}}
| CSBE: ~7/6 = 271.5741{{c}}
|}
|}
[6 5/2] eigenmonzos: [[orwellwoo13|orwellwoo13]] [[orwellwoo22|orwellwoo22]]


=MOSes=
{| class="wikitable mw-collapsible mw-collapsed"
 
|+ style="font-size: 105%; white-space: nowrap;" | 11-limit prime-optimized tunings
==9-note (LsLsLsLss, proper)==
|-
[[file:OrwellNonatonicPOTE.mp3]] in POTE tuning
! rowspan="2" |
 
! colspan="2" | Euclidean
[[file:OrwellNonatonic22edo.mp3]] in 22edo
 
[[file:OrwellNonatonic53edo.mp3]] in 53edo
 
{| class="wikitable"
|-
|-
| | Small ("minor") interval
! Constrained
| | 114.29
! Constrained & skewed
| | 228.59
| | 385.72
| | 500.02
| | 657.15
| | 771.44
| | 928.57
| | 1042.87
|-
|-
| | JI intervals represented
! Equilateral
| | 15/14~16/15
| CEE: ~7/6 = 271.4920{{c}}
| | 8/7
| CSEE: ~7/6 = 271.3038{{c}}
| | 5/4
| | 4/3
| | 16/11
| | 14/9~11/7
| | 12/7
| | 11/6
|-
|-
| | Large ("major") interval
! Tenney
| | 157.13
| CTE: ~7/6 = 271.5597{{c}}
| | 271.43
| CWE: ~7/6 = 271.4552{{c}}
| | 428.56
| | 542.85
| | 699.98
| | 814.28
| | 971.41
| | 1085.71
|-
|-
| | JI intervals represented
! Benedetti, <br>Wilson
| | 12/11~11/10
| CBE: ~7/6 = 271.5915{{c}}
| | 7/6
| CSBE: ~7/6 = 271.5302{{c}}
| | 14/11~9/7
| | 11/8
| | 3/2
| | 8/5
| | 7/4
| | 15/8
|}
|}


==13-note (LLLsLLsLLsLLs, improper)==
{| class="wikitable mw-collapsible mw-collapsed"
|+ style="font-size: 105%; white-space: nowrap;" | DR and equal-beating tunings
|-
! Optimized chord !! Generator value !! Polynomial !! Further notes
|-
| 3:4:5 (+1 +1) || ~7/6 = 272.890{{c}} || ''f''<sup>10</sup> &minus; 8''f''<sup>3</sup> + 8 = 0 || 1–3–5 equal-beating tuning
|-
| 4:5:6 (+1 +1) || ~7/6 = 271.508{{c}} || ''f''<sup>10</sup> + 2''f''<sup>3</sup> - 8 = 0 || 1–3–5 equal-beating tuning
|}


{| class="wikitable"
=== Tuning spectrum ===
{| class="wikitable center-all left-4"
|-
! Edo<br>generator
! [[Eigenmonzo|Unchanged interval<br>(eigenmonzo)]]*
! Generator (¢)
! Comments
|-
| 2\9
|
| 266.667
| Lower bound of 7-odd-limit diamond monotone
|-
|
| 7/6
| 266.871
|
|-
|
| 15/11
| 268.475
|
|-
|
| 11/7
| 269.585
|
|-
|
| 11/6
| 270.127
|
|-
|
| 15/14
| 270.139
|
|-
|
| 49/48
| 270.633
|
|-
|
| 21/11
| 270.728
|
|-
| 7\31
|
| 270.968
| Lower bound of 9- and 11-odd-limit diamond monotone
|-
|
| 11/9
| 271.049
|
|-
|
| 7/4
| 271.103
|
|-
|
| 7/5
| 271.137
| 7- and 11-odd-limit minimax
|-
|
| 5/4
| 271.229
|
|-
|
| 21/20
| 271.359
|
|-
|
| 21/16
| 271.385
|
|-
| 19\84
|
| 271.429
| 84e val
|-
|
| 25/24
| 271.487
|
|-
|
| 64/63
| 271.488
|
|-
|
| 5/3
| 271.564
| 5-odd-limit minimax
|-
|
| 9/5
| 271.623
| 9-odd-limit minimax
|-
|
| 81/80
| 271.661
|
|-
| 12\53
|
| 271.698
|
|-
|
| 3/2
| 271.708
|
|-
| 17\75
|
| 272.000
|
|-
|
| 15/8
| 272.067
|
|-
|
| 36/35
| 272.086
|
|-
|-
| | Small ("minor") interval
|  
| | 42.84
| 9/7
| | 157.13
| 272.514
| | 271.43
|  
| | 314.26
| | 428.56
| | 542.85
| | 585.69
| | 699.98
| | 814.28
| | 857
| | 971.41
| | 1085.71
|-
|-
| | JI intervals represented
| 5\22
| |
|  
| | 12/11~11/10
| 272.727
| | 7/6
| Upper bound of 7-, 9- and 11-odd-limit diamond monotone
| | 6/5
| | 14/11~9/7
| | 11/8
| | 7/5
| | 3/2
| | 8/5
| | 18/11
| | 7/4
| | 15/8
|-
|-
| | Large ("major") interval
|  
| | 114.29
| 11/10
| | 228.59
| 273.001
| | 342.88
|  
| | 385.72
| | 500.02
| | 614.31
| | 657.15
| | 771.44
| | 885.74
| | 928.57
| | 1042.87
| | 1157.16
|-
|-
| | JI intervals represented
|  
| | 15/14~16/15
| 11/8
| | 8/7
| 275.659
| | 11/9
|  
| | 5/4
| | 4/3
| | 10/7
| | 16/11
| | 14/9~11/7
| | 5/3
| | 12/7
| | 11/6
| |
|}
|}
<nowiki/>* Besides the octave
== Non-octave settings ==
=== Watcher ===
By switching the roles of the period and generator, we end up with a nonoctave temperament that is to orwell what [[angel]] and [[devadoot]] are to [[meantone]] and [[magic]], respectively. There is an interesting mos with 7 notes per period; if this is derived as a subset of [[84edt]] (which has 12 notes per period, and is almost identical to 53edo), the resulting mos has the same structure as the 12edo diatonic scale, only compressed so that the period is ~272 cents rather than an octave. Thus, a piano keyboard for this mos would look exactly the same as a typical keyboard, only what looks like an octave would not be one anymore. This temperament could be called [[Wikipedia: Watcher (angel)|watcher]], a reference to a class of angels whose very name carries Orwellian connotations. The 12-integer-limit otonality (1::12) and utonality (1/(1::12)) both have complexity 4. If we consider these to be the fundamental consonances, then using the 7-note-per-period mos, there are exactly 3 of each type per period, which again is analogous to the diatonic scale. While angel and devadoot do not perform well past the 10-integer-limit, watcher handles the 12-integer-limit with ease. Straight-fretted watcher guitars could be built as long as the strings were all tuned to period-equivalent notes.


=Planar temperaments=
== Rank-3 temperaments ==
Following is a list of rank three, or planar temperaments that are supported by orwell temperament.
Following is a list of rank-3, or planar temperaments that are supported by orwell temperament.


{| class="wikitable"
{| class="wikitable"
|-
|-
! colspan="2" | Planar temperament
! colspan="2" | Rank-3 temperament
! colspan="4" | Among others, planar temperament is also supported by...
! colspan="4" | Among others, rank-3 temperament is also supported by…
|-
|-
! | 7-limit
! 7-limit
! | 11-limit
! 11-limit<br>Extension
 
! 9tet
extension
! 22tet
! | 9tet
! 31tet
! | 22tet
! 53tet
! | 31tet
! | 53tet
|-
|-
| | [[Marvel_family|marvel]]
| [[Marvel family|Marvel]]
| |
|  
| | negri, septimin, august,
| Negri, septimin, august,<br>amavil, enneaportent
 
| Magic, pajara, wizard, porky
amavil, enneaportent
| Meantone, miracle, tritonic,<br>slender, würschmidt
| | magic, pajara, wizard, porky
| Garibaldi, catakleismic
| | meantone, miracle, tritonic,
 
slender, würschmidt
| | garibaldi, catakleismic
|-
|-
| |
|  
| | marvel
| Marvel
| | negri, septimin, enneaportent
| Negri, septimin, enneaportent
| | magic, pajarous, wizard
| Magic, pajarous, wizard
| | meanpop, miracle, tritoni, slender
| Meanpop, miracle, tritoni, slender
| | garibaldi, catakleismic
| Garibaldi, catakleismic
|-
|-
| |
|  
| | minerva
| Minerva
| | negric, august, amavil
| Negric, august, amavil
| | telepathy, pajara
| Telepathy, pajara
| | meantone, revelation, würschmidt
| Meantone, revelation, würschmidt
| | cataclysmic
| Cataclysmic
|-
|-
| |
|  
| | artemis*
| Artemis*
| | wilsec
| Wilsec
| | divination, hemipaj, porky
| Divination, hemipaj, porky
| | migration, oracle, tritonic
| Migration, oracle, tritonic
| |
|  
|-
|-
| | [[Porwell_family|hewuermity]]
| [[Porwell family|Hewuermity]]
| |
|  
| | triforce, armodue,
| Triforce, armodue,<br>twothirdtonic
 
| Porcupine, astrology, shrutar,<br>hendecatonic, septisuperfourth
twothirdtonic
| Hemiwürschmidt, valentine,<br>mohajira, grendel
| | porcupine, astrology, shrutar,
| Amity, hemischis,<br>hemikleismic
 
hendecatonic, septisuperfourth
| | hemiwürschmidt, valentine,
 
mohajira, grendel
| | amity, hemischis,
 
hemikleismic
|-
|-
| |
|  
| | zeus
| Zeus
| | triforce, armodue,
| Triforce, armodue,<br>twothirdtonic
 
| Porcupine, astrology, shrutar,<br>hendecatonic
twothirdtonic
| Hemiwur, valentine, mohajira
| | porcupine, astrology, shrutar,
| Hitchcock,<br>hemikleismic
 
hendecatonic
| | hemiwur, valentine, mohajira
| | hitchcock,
 
hemikleismic
|-
|-
| |
|  
| | jupiter
| Jupiter
| |
|  
| | septisuperfourth
| Septisuperfourth
| | hemiwürschmidt, grendel
| Hemiwürschmidt, grendel
| | amity, hemischis
| Amity, hemischis
|-
|-
| | [[Orwellismic_family|orwellian]]
| [[Orwellismic family|Orwellismic]]
| |
|  
| | beep, secund, infraorwell,
| Beep, secund, infraorwell,<br>niner
 
| Superpyth, doublewide,<br>echidna
niner
| Myna, mothra, sentinel,<br>semisept
| | superpyth, doublewide,
| Quartonic, buzzard
 
echidna
| | myna, mothra, sentinel,
 
semisept
| | quartonic, buzzard
|-
|-
| |
|  
| | orwellian
| Orwellian
| | pentoid, secund
| Pentoid, secund
| | suprapyth, doublewide
| Suprapyth, doublewide
| | myno, mothra, sentinel
| Myno, mothra, sentinel
| |
|  
|-
|-
| |
|  
| | guanyin
| Guanyin
| | infraorwell, niner
| Infraorwell, niner
| | superpyth, fleetwood, echidna
| Superpyth, fleetwood, echidna
| | myna, mosura, semisept
| Myna, mosura, semisept
| | quartonic, buzzard
| Quartonic, buzzard
|-
|-
| | [[Nuwell_family|nuwell]]
| [[Nuwell family|Nuwell]]
| |
|  
| | progression, superpelog
| Progression, superpelog
| | quasisuper, hedgehog
| Quasisuper, hedgehog
| | squares, nusecond
| Squares, nusecond
| | tricot, hamity
| Tricot, hamity
|-
|-
| |
|  
| | big brother
| Big brother
| | progression, superpelog
| Progression, superpelog
| | quasisupra, hedgehog
| Quasisupra, hedgehog
| | squares, nusecond
| Squares, nusecond
| | tricot, hamity
| Tricot, hamity
|-
|-
| | [[Horwell_family|horwell]]
| [[Horwell family|Horwell]]
| |
|  
| |
|  
| | bisupermajor, escaped,
| Bisupermajor, escaped,<br>fifthplus
 
| Hemithirds, worschmidt,<br>tertiaseptal
fifthplus
| Countercata, pontiac
| | hemithirds, worschmidt,
 
tertiaseptal
| | countercata, pontiac
|-
|-
| |
|  
| | zelda
| Zelda
| |
|  
| | bisupermajor, sensa
| Bisupermajor, sensa
| | hemithirds, worschmidt, tertia
| Hemithirds, worschmidt, tertia
| | countercata
| Countercata
|}
|}
*weak extension (one or more generators from the parent temperament are split)
<nowiki/>* [[Weak extension]] (one or more generators from the parent temperament are split)


=[[Chords_of_orwell|Chords of orwell]]=
== Music ==
; [[Tarkan Grood]]
* ''Mountain Villiage'' (2013) – [https://web.archive.org/web/20201127012514/http://micro.soonlabel.com/gene_ward_smith/Others/Grood/Mountain_Village_TarkanGrood.mp3 play] | [https://soundcloud.com/tarkan-grood/mountain-village-tarkangrood SoundCloud] – in Orwell[9]


=MOS transversals=
; [[Andrew Heathwaite]]
[[orwell13trans|orwell13trans]]
* ''[[Earwig]]'' (2012) – [https://web.archive.org/web/20201127015238/http://micro.soonlabel.com/gene_ward_smith/Others/Heathwaite/earwig.mp3 play] – in 31edo tuning
* [[Technical Notes for Newbeams #Elf Dine on Ho Ho|''Elf Dine on Ho Ho'']] (2012) – [https://web.archive.org/web/20201127015137/http://micro.soonlabel.com/gene_ward_smith/Others/Heathwaite/Newbeams/Andrew%20Heathwaite%20-%20Newbeams%20-%2004%20Hypnocloudsmack%201.mp3 play] – in 53edo tuning
* [[Technical Notes for Newbeams #Spun|''Spun'']] (2012) – [https://web.archive.org/web/20201112021340/http://micro.soonlabel.com/gene_ward_smith/Others/Heathwaite/Newbeams/Andrew%20Heathwaite%20-%20Newbeams%20-%2008%20Spun.mp3 play] – in Orwell[13]
* [https://web.archive.org/web/20201127013436/http://micro.soonlabel.com/gene_ward_smith/Others/Heathwaite/andrewheathwaite+onedropofrain.mp3 ''one drop of rain'']
* [https://web.archive.org/web/20201127014501/http://micro.soonlabel.com/gene_ward_smith/Others/Heathwaite/andrewheathwaite+ivecomewithabucketofroses.mp3 ''i've come with a bucket of roses'']
* [https://web.archive.org/web/20201127014830/http://micro.soonlabel.com/gene_ward_smith/Others/Heathwaite/andrewheathwaite+myownhouse.mp3 ''my own house'']


[[orwell22trans|orwell22trans]]
; [[Peter Kosmorsky]]
* ''Tunicata and Fugue'' – [http://www.archive.org/details/TunicataAndFugue details] | [http://archive.org/download/TunicataAndFugue/TunicataAndFugueVer2.mp3 play]


[[orwell31trans|orwell31trans]]
; [[Löis Lancaster]] ([[Roncevaux]])
* ''Schizo Blue'' – [https://web.archive.org/web/20201127012220/http://micro.soonlabel.com/gene_ward_smith/Others/Roncevaux/Schizo_Blue__22_EDO_Orwell__first_mix_by_Roncevaux_on_SoundCloud___Hear_the_world_s_sounds.mp3 play] | [https://soundcloud.com/lois-lancaster/schizo-blue-22-edo-orwell SoundCloud]{{dead link}}
* ''Sejaliscos'' (2013) – [https://web.archive.org/web/20201127012431/http://micro.soonlabel.com/gene_ward_smith/Others/Roncevaux/Sejaliscos_by_Roncevaux_on_SoundCloud___Hear_the_world_s_sounds.mp3 play] | [https://soundcloud.com/lois-lancaster/sejaliscos SoundCloud] – in Orwell[9], 22edo tuning


[[orwell13trans57|orwell13trans57]]
; [[Claudi Meneghin]]
* [https://www.youtube.com/watch?v=zWrOiih7raY ''Orwell Canon 3 in 1 upon a Ground for Baroque Oboe, Viola, Clarinet, and Viola da Gamba''] (2024)


[[orwell22trans57|orwell22trans57]]
; [[Herman Miller]]
* ''[https://soundcloud.com/morphosyntax-1/a-hidden-world A Hidden World]'' (2022) – in Orwell[31]
* ''[https://soundcloud.com/morphosyntax-1/zurg-tuun-vantu-war-is-peace Zurğ tuun vantu]'' (2024) – in Orwell[13], with a generator of 271.5{{c}} and a period of 1199.5{{c}}


[[orwell31trans57|orwell31trans57]]
; [[Sevish]]
* "[[Droplet]]", from ''[[Rhythm and Xen]]'' (2015) – [https://sevish.bandcamp.com/track/droplet Bandcamp] | [https://soundcloud.com/sevish/droplet?in=sevish/sets/rhythm-and-xen SoundCloud] | [https://www.youtube.com/watch?v=xVZy9GUeMqY YouTube] – drum and bass in Orwell[9], 53edo tuning


=Music=
; [[Gene Ward Smith]]
[http://www.archive.org/details/TrioInOrwell Trio in Orwell] [http://www.archive.org/download/TrioInOrwell/TrioInOrwell.mp3 play] by [[Gene_Ward_Smith|Gene Ward Smith]]
* ''Trio in Orwell'' (archived 2010) – [http://www.archive.org/details/TrioInOrwell details] | [http://www.archive.org/download/TrioInOrwell/TrioInOrwell.mp3 play] – in Orwell[9], 53edo tuning
* [https://web.archive.org/web/20201112015404/http://micro.soonlabel.com/gene_ward_smith/transformers/swing-orwell9.mp3 ''Swing in Orwell-9'']


[[earwig|earwig]], [http://micro.soonlabel.com/gene_ward_smith/Others/Heathwaite/earwig.mp3 play],
; [[Chris Vaisvil]]
* [https://web.archive.org/web/20201127014716/http://micro.soonlabel.com/orwell/daily20100721-gpo-owellian-cameras.mp3 ''Orwellian Cameras'']


[[Technical_Notes_for_Newbeams#Track notes:-Elf Dine on Ho Ho|Elf Dine on Ho Ho]], [http://micro.soonlabel.com/gene_ward_smith/Others/Heathwaite/Newbeams/Andrew%20Heathwaite%20-%20Newbeams%20-%2004%20Hypnocloudsmack%201.mp3 play],
== Keyboards ==
{{See also| Orwell on an isomorphic keyboard }}
{{See also| Lumatone mapping for orwell}}


[[Technical_Notes_for_Newbeams#Track notes:-Spun|Spun]], [http://micro.soonlabel.com/gene_ward_smith/Others/Heathwaite/Newbeams/Andrew%20Heathwaite%20-%20Newbeams%20-%2008%20Spun.mp3 play],
To play interactive versions of these keyboards, check out [https://github.com/vsicurella/SuperVirtualKeyboard Vito Sicurella's plugin], which works with REAPER:


[http://micro.soonlabel.com/gene_ward_smith/Others/Heathwaite/andrewheathwaite+onedropofrain.mp3 one drop of rain], [http://micro.soonlabel.com/gene_ward_smith/Others/Heathwaite/andrewheathwaite+onedropofrain.mp3 play],
[[File:Orwell_13.png|alt=Orwell_13.png|1023x292px|Orwell_13.png]]
 
[http://micro.soonlabel.com/gene_ward_smith/Others/Heathwaite/andrewheathwaite+ivecomewithabucketofroses.mp3 i've come with a bucket of roses] and [http://micro.soonlabel.com/gene_ward_smith/Others/Heathwaite/andrewheathwaite+myownhouse.mp3 my own house] by [[Andrew_Heathwaite|Andrew Heathwaite]]
 
[http://micro.soonlabel.com/orwell/daily20100721-gpo-owellian-cameras.mp3 Orwellian Cameras] by [[Chris_Vaisvil|Chris Vaisvil]]
 
[http://archive.org/download/TunicataAndFugue/TunicataAndFugueVer2.mp3 Tunicata and Fugue] by [http://www.archive.org/details/TunicataAndFugue Peter Kosmorsky]
 
[https://soundcloud.com/tarkan-grood/mountain-village-tarkangrood Mountain Villiage] [http://micro.soonlabel.com/gene_ward_smith/Others/Grood/Mountain_Village_TarkanGrood.mp3 play] by Tarkan Grood
 
[http://micro.soonlabel.com/gene_ward_smith/transformers/swing-orwell9.mp3 Swing in Orwell-9]
 
[http://micro.soonlabel.com/gene_ward_smith/Others/Roncevaux/Schizo_Blue__22_EDO_Orwell__first_mix_by_Roncevaux_on_SoundCloud___Hear_the_world_s_sounds.mp3 Schizo Blue] by [https://soundcloud.com/lois-lancaster/schizo-blue-22-edo-orwell Roncevaux (Löis Lancaster)]
 
[http://micro.soonlabel.com/gene_ward_smith/Others/Roncevaux/Sejaliscos_by_Roncevaux_on_SoundCloud___Hear_the_world_s_sounds.mp3 Sejaliscos] by [https://soundcloud.com/lois-lancaster/sejaliscos Roncevaux]
 
=Keyboards=
To play interactive versions of these keyboards, check out Vito Sicurella's plugin, which works with REAPER:


<nowiki>https://github.com/vsicurella/SuperVirtualKeyboard/releases/tag/0.021?fbclid=IwAR0ShCAy672Ruaz1VSVaU2beGuX2RI3elIfZOyrn9T9OHOYuQNXTGBCyIgU</nowiki>
[[File:Orwell_22.png|alt=Orwell_22.png|1023x292px|Orwell_22.png]]
 
[[File:Orwell_13.png|alt=Orwell_13.png|1023x292px|Orwell_13.png]]


=[[File:Orwell_22.png|alt=Orwell_22.png|1023x292px|Orwell_22.png]]=
[[File:orwell13_axis49.png|alt=orwell13_axis49.png|orwell13_axis49.png]]
[[File:orwell13_axis49.png|alt=orwell13_axis49.png|orwell13_axis49.png]]


See: [[Orwell_on_an_Isomorphic_Keyboard|Orwell on an Isomorphic Keyboard]]    
[[Category:Orwell| ]] <!-- main article -->
[[Category:11-limit]]
[[Category:Rank-2 temperaments]]
[[Category:7-limit]]
[[Category:Semicomma family]]
[[Category:84edo]]
[[Category:Marvel temperaments]]
[[Category:mos]]
[[Category:Orwellismic temperaments]]
[[Category:orwell]]
[[Category:Listen]]
[[Category:semicomma]]
[[Category:temperament]]

Latest revision as of 11:58, 6 August 2025

Martin Aurell's diagram showing Orwell[9] generated in 31 tone equal temperament.

Orwell – so named because 19 steps of 84edo, i.e. 19\84, is a possible generator – is an excellent 7-limit temperament and an amazing 11-limit temperament because of the simplicity of harmonic 11.

In orwell, the just perfect twelfth (3/1) is divided into 7 equal steps. One of these steps represents 7/6; three represent 8/5. Alternately, the 5th harmonic (5/1) divided into 3 equal steps also makes a good orwell generator, being ~12/7.

In the 11-limit, two generators are equated to 11/8 (meaning 99/98 is tempered out). This means that three stacked generators makes the orwell tetrad 1–7/6–11/8–8/5, a chord in which every interval is a (tempered) 11-odd-limit consonance. Other such chords in orwell are the keenanismic chords and the swetismic chords.

Compatible equal temperaments include 22edo, 31edo, 53edo, and 84edo. Orwell is in better tune in lower limits than higher ones; the optimal patent val is 296edo in the 5-limit, 137edo in the 7-limit, and 53edo in the 11-limit. It tempers out the semicomma in the 5-limit, and so belongs to the semicomma family. In the 7-limit it tempers out 225/224, 1728/1715, 2430/2401 and 6144/6125, and in the 11-limit, 99/98, 121/120, 176/175, 385/384 and 540/539. By adding 275/273 to the list of commas it can be extended to the 13-limit as tridecimal orwell, and by adding instead 66/65, winston temperament. See Orwell extensions for details about 13-limit extensions.

See Semicomma family #Orwell for technical details.

Interval chain

Odd harmonics 1–21 and their inverses are in bold.

# Cents* Approximate ratios
0 0.00 1/1
1 271.46 7/6
2 542.91 11/8, 15/11
3 814.37 8/5
4 1085.82 15/8, 28/15
5 157.28 11/10, 12/11, 35/32
6 428.73 9/7, 14/11, 32/25
7 700.19 3/2
8 971.64 7/4
9 43.10 33/32, 36/35, 49/48
10 314.55 6/5
11 586.01 7/5
12 857.46 18/11
13 1128.92 21/11, 27/14, 48/25
14 200.37 9/8, 28/25
15 471.83 21/16
16 743.28 49/32, 54/35
17 1014.74 9/5
18 86.19 21/20
19 357.65 27/22, 49/40
20 629.10 36/25
21 900.56 27/16, 42/25
22 1172.01 63/32

* In 11-limit CWE tuning, octave reduced

Chords and harmony

Main article: Chords of orwell
See also: Functional harmony in rank-2 temperaments

The fundamental otonal consonance of orwell, voiced in a roughly tertian manner, is 4:5:6:7:9:11. In terms of generator steps this is 0–(−3)–7–8–14–2, only available in a 22-tone mos. However, some subsets of this chord are way simpler, such as 8:11:12:14, which is 1–11/8–3/2–7/4 (0–2–7–8).

The generator, ~7/6, is a septimal interval, so chords could instead be built around it as 1–7/6–3/2 (0–1–7), 1–7/4–3 (0–8–7), or tetrads such as 1–7/6–3/2–7/4 (0–1–7–8).

To 1–7/6–3/2–7/4 we may add 11/8, or to 1–11/8–3/2–7/4 we may add 7/6, to form an essentially tempered pentad, 1–7/6–11/8–3/2–7/4 (0–1–2–7–8). Its inverse is 1–12/11–9/7–3/2–12/7 (0–5–6–7–(−1)), which can serve as a minor counterpart. This is similar, but also in clear contrast to the 1–5/4–3/2 (0–4–1) and 1–6/5–3/2 (0–(−3)–1) chords of meantone. Two approaches to functional harmony thus arise.

First, we can treat the septimal chords above as the basis of harmony, but swapping the roles of 3 and 7 according to their temperamental complexities (number of generator steps). Thus a "dominant" chord is either 7/6 or 12/7 over tonic; a "subdominant" chord is either 7/6 or 12/7 under tonic. This leads to an approach closely adherent to mos scales. The 9-tone mos contains a tonic and a "dominant" triad. The 13-tone mos is good for encapsulating tonic, "pre-dominant", and "dominant" functions, triads to pentads alike.

Second, we can treat the same chords as the basis of harmony, and keeping the role of the chain of fifths as the spine on which the functions are defined. This means dominant is still 3/2 over tonic, for example. A consequence is we must step out of the logic of mos scales, as they are often too restrictive without the many fifths to stack. This is essentially working in JI, but using the commas tempered out in some way to lock into the identity of the temperament.

Scales

Main article: Orwell scales

Mos scales

9-tone scales (sLsLsLsLs, proper)

in POTE tuning

in 22edo

in 53edo

Small ("minor") interval 114.29 228.59 385.72 500.02 657.15 771.44 928.57 1042.87
JI intervals represented 15/14~16/15 8/7 5/4 4/3 16/11 14/9~11/7 12/7 11/6
Large ("major") interval 157.13 271.43 428.56 542.85 699.98 814.28 971.41 1085.71
JI intervals represented 12/11~11/10 7/6 14/11~9/7 11/8 3/2 8/5 7/4 15/8
13-tone scales (LsLLsLLLsLLsL, improper)
Small ("minor") interval 42.84 157.13 271.43 314.26 428.56 542.85 585.69 699.98 814.28 857 971.41 1085.71
JI intervals represented 12/11~11/10 7/6 6/5 14/11~9/7 11/8 7/5 3/2 8/5 18/11 7/4 15/8
Large ("major") interval 114.29 228.59 342.88 385.72 500.02 614.31 657.15 771.44 885.74 928.57 1042.87 1157.16
JI intervals represented 15/14~16/15 8/7 11/9 5/4 4/3 10/7 16/11 14/9~11/7 5/3 12/7 11/6
22-tone scales

Transversal scales

Others

Tunings

7-limit prime-optimized tunings
Euclidean
Constrained Constrained & skewed
Equilateral CEE: ~7/6 = 271.3553 ¢ CSEE: ~7/6 = 271.3339 ¢
Tenney CTE: ~7/6 = 271.5130 ¢ CWE: ~7/6 = 271.5097 ¢
Benedetti,
Wilson 		CBE: ~7/6 = 271.5725 ¢ CSBE: ~7/6 = 271.5741 ¢
11-limit prime-optimized tunings
Euclidean
Constrained Constrained & skewed
Equilateral CEE: ~7/6 = 271.4920 ¢ CSEE: ~7/6 = 271.3038 ¢
Tenney CTE: ~7/6 = 271.5597 ¢ CWE: ~7/6 = 271.4552 ¢
Benedetti,
Wilson 		CBE: ~7/6 = 271.5915 ¢ CSBE: ~7/6 = 271.5302 ¢
DR and equal-beating tunings
Optimized chord Generator value Polynomial Further notes
3:4:5 (+1 +1) ~7/6 = 272.890 ¢ f10 − 8f3 + 8 = 0 1–3–5 equal-beating tuning
4:5:6 (+1 +1) ~7/6 = 271.508 ¢ f10 + 2f3 - 8 = 0 1–3–5 equal-beating tuning

Tuning spectrum

Edo
generator 		Unchanged interval
(eigenmonzo)* 		Generator (¢) Comments
2\9 266.667 Lower bound of 7-odd-limit diamond monotone
7/6 266.871
15/11 268.475
11/7 269.585
11/6 270.127
15/14 270.139
49/48 270.633
21/11 270.728
7\31 270.968 Lower bound of 9- and 11-odd-limit diamond monotone
11/9 271.049
7/4 271.103
7/5 271.137 7- and 11-odd-limit minimax
5/4 271.229
21/20 271.359
21/16 271.385
19\84 271.429 84e val
25/24 271.487
64/63 271.488
5/3 271.564 5-odd-limit minimax
9/5 271.623 9-odd-limit minimax
81/80 271.661
12\53 271.698
3/2 271.708
17\75 272.000
15/8 272.067
36/35 272.086
9/7 272.514
5\22 272.727 Upper bound of 7-, 9- and 11-odd-limit diamond monotone
11/10 273.001
11/8 275.659

* Besides the octave

Non-octave settings

Watcher

By switching the roles of the period and generator, we end up with a nonoctave temperament that is to orwell what angel and devadoot are to meantone and magic, respectively. There is an interesting mos with 7 notes per period; if this is derived as a subset of 84edt (which has 12 notes per period, and is almost identical to 53edo), the resulting mos has the same structure as the 12edo diatonic scale, only compressed so that the period is ~272 cents rather than an octave. Thus, a piano keyboard for this mos would look exactly the same as a typical keyboard, only what looks like an octave would not be one anymore. This temperament could be called watcher, a reference to a class of angels whose very name carries Orwellian connotations. The 12-integer-limit otonality (1::12) and utonality (1/(1::12)) both have complexity 4. If we consider these to be the fundamental consonances, then using the 7-note-per-period mos, there are exactly 3 of each type per period, which again is analogous to the diatonic scale. While angel and devadoot do not perform well past the 10-integer-limit, watcher handles the 12-integer-limit with ease. Straight-fretted watcher guitars could be built as long as the strings were all tuned to period-equivalent notes.

Rank-3 temperaments

Following is a list of rank-3, or planar temperaments that are supported by orwell temperament.

Rank-3 temperament Among others, rank-3 temperament is also supported by…
7-limit 11-limit
Extension 		9tet 22tet 31tet 53tet
Marvel Negri, septimin, august,
amavil, enneaportent 		Magic, pajara, wizard, porky Meantone, miracle, tritonic,
slender, würschmidt 		Garibaldi, catakleismic
Marvel Negri, septimin, enneaportent Magic, pajarous, wizard Meanpop, miracle, tritoni, slender Garibaldi, catakleismic
Minerva Negric, august, amavil Telepathy, pajara Meantone, revelation, würschmidt Cataclysmic
Artemis* Wilsec Divination, hemipaj, porky Migration, oracle, tritonic
Hewuermity Triforce, armodue,
twothirdtonic 		Porcupine, astrology, shrutar,
hendecatonic, septisuperfourth 		Hemiwürschmidt, valentine,
mohajira, grendel 		Amity, hemischis,
hemikleismic
Zeus Triforce, armodue,
twothirdtonic 		Porcupine, astrology, shrutar,
hendecatonic 		Hemiwur, valentine, mohajira Hitchcock,
hemikleismic
Jupiter Septisuperfourth Hemiwürschmidt, grendel Amity, hemischis
Orwellismic Beep, secund, infraorwell,
niner 		Superpyth, doublewide,
echidna 		Myna, mothra, sentinel,
semisept 		Quartonic, buzzard
Orwellian Pentoid, secund Suprapyth, doublewide Myno, mothra, sentinel
Guanyin Infraorwell, niner Superpyth, fleetwood, echidna Myna, mosura, semisept Quartonic, buzzard
Nuwell Progression, superpelog Quasisuper, hedgehog Squares, nusecond Tricot, hamity
Big brother Progression, superpelog Quasisupra, hedgehog Squares, nusecond Tricot, hamity
Horwell Bisupermajor, escaped,
fifthplus 		Hemithirds, worschmidt,
tertiaseptal 		Countercata, pontiac
Zelda Bisupermajor, sensa Hemithirds, worschmidt, tertia Countercata

* Weak extension (one or more generators from the parent temperament are split)

Music

Tarkan Grood
Andrew Heathwaite
Peter Kosmorsky
Löis Lancaster (Roncevaux)
Claudi Meneghin
Herman Miller
Sevish
Gene Ward Smith
Chris Vaisvil

Keyboards

See also: Orwell on an isomorphic keyboard
See also: Lumatone mapping for orwell

To play interactive versions of these keyboards, check out Vito Sicurella's plugin, which works with REAPER:

Orwell_13.png

Orwell_22.png

orwell13_axis49.png

Retrieved from "https://en.xen.wiki/index.php?title=Orwell&oldid=206414"