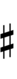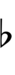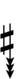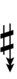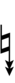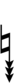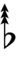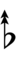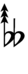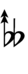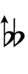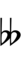56edo

From Xenharmonic Wiki
(Redirected from 56 EDO)
Jump to navigation Jump to search
← 55edo 56edo 57edo →
Prime factorization 23 × 7
Step size 21.4286 ¢ 
Fifth 33\56 (707.143 ¢)
Semitones (A1:m2) 7:3 (150 ¢ : 64.29 ¢)
Consistency limit 7
Distinct consistency limit 7

56 equal divisions of the octave (abbreviated 56edo or 56ed2), also called 56-tone equal temperament (56tet) or 56 equal temperament (56et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 56 equal parts of about 21.4 ¢ each. Each step represents a frequency ratio of 21/56, or the 56th root of 2.

Theory

56edo shares its near perfect quality of classical major third with 28edo, which it doubles, while also adding a superpythagorean 5th that is a convergent towards the bronze metallic mean, following 17edo and preceding 185edo. Because it contains 28edo's major third and also has a step size very close to the syntonic comma, 56edo contains very accurate approximations of both the classic major third 5/4 and the Pythagorean major third 81/64. Unfortunately, this "Pythagorean major third" is not the major third as is stacked by fifths in 56edo.

56edo can be used to tune hemithirds, superkleismic, sycamore and keen temperaments, and using ⟨56 89 130 158] (56d) as the equal temperament val, for pajara. It provides the optimal patent val for 7-, 11- and 13-limit sycamore, and the 11-limit 56d val is close to the POTE tuning for 11-limit pajara.

Prime harmonics

Approximation of prime harmonics in 56edo
Harmonic 2 3 5 7 11 13 17 19 23 29 31
Error Absolute (¢) +0.00 +5.19 -0.60 -4.54 +5.82 -4.81 +2.19 +2.49 -6.85 -1.01 -9.32
Relative (%) +0.0 +24.2 -2.8 -21.2 +27.2 -22.5 +10.2 +11.6 -31.9 -4.7 -43.5
Steps
(reduced) 		56
(0) 		89
(33) 		130
(18) 		157
(45) 		194
(26) 		207
(39) 		229
(5) 		238
(14) 		253
(29) 		272
(48) 		277
(53)

Subsets and supersets

Since 56 factors into 23 × 7, 56edo has subset edos 2, 4, 7, 8, 14, 28.

One step of 56edo is the closest direct approximation to the syntonic comma, 81/80, with the unrounded value being 55.7976. Barium temperament realizes this proximity through regular temperament theory, and is supported by notable edos like 224edo, 1848edo, and 2520edo, which is a highly composite edo.

Intervals

# Cents Approximate ratios* Ups and downs notation
0 0.0 1/1 D
1 21.4 49/48, 55/54, 56/55, 64/63 ^D, vvE♭
2 42.9 28/27, 40/39, 45/44, 50/49, 81/80 ^^D, vE♭
3 64.3 25/24, 36/35, 33/32 ^3D, E♭
4 85.7 19/18, 20/19, 21/20, 22/21 v3D♯, ^E♭
5 107.1 16/15, 17/16, 18/17 vvD♯, ^^E♭
6 128.6 15/14, 13/12, 14/13 vD♯, ^3E♭
7 150.0 12/11 D♯, v3E
8 171.4 10/9, 11/10, 21/19 ^D♯, vvE
9 192.9 19/17, 28/25 ^^D♯, vE
10 214.3 9/8, 17/15 E
11 235.7 8/7 ^E, vvF
12 257.1 7/6 ^^E, vF
13 278.6 13/11, 20/17 F
14 300.0 19/16, 25/21 ^F, vvG♭
15 321.4 6/5 ^^F, vG♭
16 342.9 11/9, 17/14 ^3F, G♭
17 364.3 16/13, 21/17, 26/21 v3F♯, ^G♭
18 385.7 5/4 vvF♯, ^^G♭
19 407.1 14/11, 19/12, 24/19 vF♯, ^3G♭
20 428.6 32/25, 33/26 F♯, v3G
21 450.0 9/7, 13/10 ^F♯, vvG
22 471.4 17/13, 21/16 ^^F♯, vG
23 492.9 4/3 G
24 514.3 35/26 ^G, vvA♭
25 535.7 15/11, 19/14, 26/19, 27/20 ^^G, vA♭
26 557.1 11/8 ^3G, A♭
27 578.6 7/5 v3G♯, ^A♭
28 600.0 17/12, 24/17 vvG♯, ^^A♭
… … … …

* The following table assumes the 19-limit patent val; other approaches are possible. Inconsistent intervals are marked in italics.

Notation

Ups and downs notation

56edo can be notated using ups and downs. Trup is equivalent to quudsharp, trudsharp is equivalent to quup, etc.

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Sharp symbol                
                 
Flat symbol              
                 

Alternatively, sharps and flats with arrows borrowed from Helmholtz–Ellis notation can be used:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
Sharp symbol  
Flat symbol

Sagittal notation

This notation uses the same sagittal sequence as 63-EDO.

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation64/6381/8033/32

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation64/6381/8033/32

Approximation to JI

The following tables show how 15-odd-limit intervals are represented in 56edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 56edo (direct approximation, even if inconsistent)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
13/7, 14/13 0.273 1.3
5/4, 8/5 0.599 2.8
11/6, 12/11 0.637 3.0
15/11, 22/15 1.236 5.8
7/5, 10/7 3.941 18.4
13/10, 20/13 4.214 19.7
7/4, 8/7 4.540 21.2
11/9, 18/11 4.551 21.2
15/8, 16/15 4.588 21.4
13/8, 16/13 4.813 22.5
3/2, 4/3 5.188 24.2
5/3, 6/5 5.787 27.0
11/8, 16/11 5.825 27.2
13/9, 18/13 6.239 29.1
11/10, 20/11 6.424 30.0
9/7, 14/9 6.513 30.4
15/14, 28/15 9.129 42.6
15/13, 26/15 9.402 43.9
7/6, 12/7 9.728 45.4
13/12, 24/13 10.001 46.7
11/7, 14/11 10.365 48.4
9/8, 16/9 10.376 48.4
9/5, 10/9 10.453 48.8
13/11, 22/13 10.638 49.6
15-odd-limit intervals in 56edo (patent val mapping)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
13/7, 14/13 0.273 1.3
5/4, 8/5 0.599 2.8
11/6, 12/11 0.637 3.0
15/11, 22/15 1.236 5.8
7/5, 10/7 3.941 18.4
13/10, 20/13 4.214 19.7
7/4, 8/7 4.540 21.2
11/9, 18/11 4.551 21.2
15/8, 16/15 4.588 21.4
13/8, 16/13 4.813 22.5
3/2, 4/3 5.188 24.2
5/3, 6/5 5.787 27.0
11/8, 16/11 5.825 27.2
11/10, 20/11 6.424 30.0
15/14, 28/15 9.129 42.6
15/13, 26/15 9.402 43.9
7/6, 12/7 9.728 45.4
13/12, 24/13 10.001 46.7
11/7, 14/11 10.365 48.4
9/8, 16/9 10.376 48.4
13/11, 22/13 10.638 49.6
9/5, 10/9 10.975 51.2
9/7, 14/9 14.916 69.6
13/9, 18/13 15.189 70.9

Zeta peak index

Tuning Strength Octave (cents) Integer limit
ZPI Steps
per 8ve 		Step size
(cents) 		Height Integral Gap Size Stretch Consistent Distinct
Tempered Pure
276zpi 56.00834 21.425381 6.063216 6.023344 0.931117 14.804703 1199.821313 −0.178687 8 8

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3 [89 -56⟩ [⟨56 89]] −1.64 1.63 7.64
2.3.5 2048/2025, 1953125/1889568 [⟨56 89 130]] −1.01 1.61 7.50
2.3.5.7 686/675, 875/864, 1029/1024 [⟨56 89 130 157]] −0.352 1.80 8.38
2.3.5.7.11 100/99, 245/242, 385/384, 686/675 [⟨56 89 130 157 194]] −0.618 1.69 7.90
2.3.5.7.11.13 91/90, 100/99, 169/168, 245/242, 385/384 [⟨56 89 130 157 194 207]] −0.299 1.70 7.95

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods
per 8ve 		Generator* Cents* Associated
ratio* 		Temperament
1 3\56 64.29 25/24 Sycamore
1 9\56 192.86 28/25 Hemithirds
1 11\56 235.71 8/7 Slendric
1 15\56 321.43 6/5 Superkleismic
1 25\56 535.71 15/11 Maquila (56d) / maquiloid (56)
2 11\56 235.71 8/7 Echidnic
2 23\56
(5\56) 		492.86
(107.14) 		4/3
(17/16) 		Keen / keenic
4 23\56
(5\56) 		492.86
(107.14) 		4/3
(17/16) 		Bidia (7-limit)
7 23\56
(1\56) 		492.86
(21.43) 		4/3
(250/243) 		Sevond

* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct

Scales

  • Supra7
  • Supra12
  • Subsets of echidnic[16] (6u8d):
    • Frankincense (this is the original/default tuning): 364.3 - 492.9 - 707.1 - 835.7 - 1200.0
    • Quasi-equipentatonic: 257.1 - 492.9 - 707.1 - 964.3 - 1200.0
    • Sakura-like scale containing phi: 107.1 - 492.9 - 707.1 - 835.7 - 1200.0
  • Subsets of sevond[14]
    • Evened minor pentatonic (approximated from 72edo): 321.4 - 492.9 - 685.7 - 1028.6 - 1200.0

Music

[[Bryan Deister]
Budjarn Lambeth
Claudi Meneghin

See also

Retrieved from "https://en.xen.wiki/index.php?title=56edo&oldid=200427"