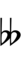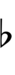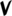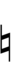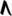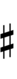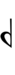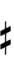45edo

← 44edo

45edo

46edo →

Prime factorization

3² × 5

Step size

26.6667 ¢

Fifth

26\45 (693.333 ¢)

Semitones (A1:m2)

2:5 (53.33 ¢ : 133.3 ¢)

Consistency limit

7

Distinct consistency limit

7

45 equal divisions of the octave (abbreviated 45edo or 45ed2), also called 45-tone equal temperament (45tet) or 45 equal temperament (45et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 45 equal parts of about 26.7 ¢ each. Each step represents a frequency ratio of 2^1/45, or the 45th root of 2.

Theory

45edo effectively has two approximate major thirds, each almost equally far from just, but as the flat one is slightly closer, it qualifies as a meantone temperament, forming a good approximation to 2/5-comma meantone. It is a flat-tending system in the 7-limit, with 3, 5, and 7 all flat, but the 11 is sharp.

It provides the optimal patent val for flattone temperament, 7-limit rank-3 avicennmic temperament tempering out 525/512, the 11-limit calliope temperament tempering out 45/44 and 81/80, and the rank-4 temperament tempering out 45/44. It tempers out 81/80, 3125/3087, 525/512, 875/864 and 45/44. It is also the unique equal temperament tuning whose patent val tempers out both the syntonic comma and the ennealimma.

45edo tempers out the quartisma and provides an excellent tuning for the 2.7/3.33 subgroup direct quartismic temperament, in which it approximates the 33/32 quartertone with 2 steps and 7/6 with 10 steps. A bit more broadly, it maps the 2.17.25.27.33.63.65 subgroup to great precision; this is the part of the 17-limit shared with 270edo.

Otherwise, it can be treated as a 2.5/3.7/3 subgroup system (borrowing 5/3 from 15edo and 7/3 from 9edo) and is a good tuning for gariberttet, defined by tempering out 3125/3087 in this subgroup, approximating 2/5-comma gariberttet.

Odd harmonics

Approximation of odd harmonics in 45edo
Harmonic		3	5	7	9	11	13	15	17	19	21	23
Error	Absolute (¢)	-8.6	-13.0	-8.8	+9.4	+8.7	+12.8	+5.1	+1.7	-4.2	+9.2	+11.7
Error	Relative (%)	-32.3	-48.7	-33.1	+35.3	+32.6	+48.0	+19.0	+6.4	-15.7	+34.6	+44.0
Steps (reduced)		71 (26)	104 (14)	126 (36)	143 (8)	156 (21)	167 (32)	176 (41)	184 (4)	191 (11)	198 (18)	204 (24)

Intervals

Step #	ET	Just (JI)		Error (ET−JI)	Ups and downs notation
Step #	Cents	Interval	Cents	Error (ET−JI)	Ups and downs notation
0	0.000	1/1	0.000	0.000	Perfect Unison	P1	D
1	26.666	65/64	26.841	-0.174	Up unison	^1	^D
2	53.333	33/32	53.273	0.060	Augmented Unison	A1	D#
3	80.000	22/21	80.537	-0.537	Diminished 2nd	d2	Ebb
4	106.666	17/16	104.955	1.711	Downminor 2nd	vm2	vEb
5	133.333	27/25	133.238	0.095	Minor 2nd	m2	Eb
6	160.000	11/10	165.004	-5.004	Mid 2nd	~2	vE
7	186.666	10/9	182.404	4.262	Major 2nd	M2	E
8	213.333	9/8	203.910	9.423	Upmajor 2nd	^M2	^E
9	240.000	8/7	231.174	8.826	Augmented 2nd	A2	E#
10	266.666	7/6	266.871	-0.205	Diminished 3rd	d3	Fb
11	293.333	32/27	294.135	-0.802	Downminor 3rd	vm3	vF
12	320.000	6/5	315.641	4.359	Minor 3rd	m3	F
13	346.666	11/9	347.408	-0.741	Mid 3rd	~3	^F
14	373.333	5/4	386.314	-12.980	Major 3rd	M3	F#
15	400.000	63/50	400.108	-0.108	Upmajor 3rd	^M3	^F#
16	426.666	9/7	435.084	-8.418	Augmented 3rd	A3	Fx
17	453.333	13/10	454.294	-0.961	Diminished 4th	d4	Gb
18	480.000	21/16	470.781	9.219	Down 4th	v4	vG
19	506.666	4/3	498.045	8.622	Perfect 4th	P4	G
20	533.333	49/36	533.742	-0.409	Up 4th or Mid 4th	^4, ~4	^G
21	560.000	18/13	563.382	-3.382	Augmented 4th	A4	G#
22	586.666	7/5	582.512	4.155	Upaugmented 4th	^A4	^G#
23	613.333	10/7	617.488	-4.155	Downdiminshed 5th	vd5	vAb
24	640.000	13/9	636.618	3.382	Diminished 5th	d5	Ab
25	666.666	72/49	666.258	0.409	Down 5th or Mid 5th	v5, ~5	vA
26	693.333	3/2	701.955	-8.622	Perfect 5th	P5	A
27	720.000	32/21	729.219	-9.219	Up 5th	^5	^A
28	746.666	20/13	745.786	0.961	Augmented 5th	A5	A#
29	773.333	14/9	764.916	8.418	Diminished 6th	d6	Bbb
30	800.000	100/63	799.892	0.108	Downminor 6th	vm6	vBb
31	826.666	8/5	813.686	12.980	Minor 6th	m6	Bb
32	853.333	18/11	852.592	0.741	Mid 6th	~6	vB
33	880.000	5/3	884.359	-4.359	Major 6th	M6	B
34	906.666	27/16	905.865	0.802	Upmajor 6th	^M6	^B
35	933.333	12/7	933.129	0.205	Augmented 6th	A6	B#
36	960.000	7/4	968.826	-8.826	Diminished 7th	d7	Cb
37	986.666	16/9	996.089	-9.423	Downminor 7th	vm7	vC
38	1013.333	9/5	1017.596	-4.262	Minor 7th	m7	C
39	1040.000	20/11	1034.996	5.004	Mid 7th	~7	^C
40	1066.666	50/27	1066.762	-0.095	Major 7th	M7	C#
41	1093.333	32/17	1095.044	-1.711	Upmajor 7th	^M7	^C#
42	1120.000	21/11	1119.463	0.537	Augmented 7th	A7	Cx
43	1146.666	64/33	1146.727	-0.060	Diminished 8ve	d8	Db
44	1173.333	128/65	1173.158	0.174	Down 8ve	v8	vD
45	1200.000	2/1	1200.000	0.000	Perfect Octave	P8	D

Notation

Ups and Downs notation

Spoken as up, sharp, upsharp, etc. Note that up can be respelled as downsharp.

Step offset	−4	−3	−2	−1	0	+1	+2	+3	+4
Symbol

Quarter-tone notation

Since a sharp raises by two steps, quarter-tone accidentals can also be used.

Step offset	−4	−3	−2	−1	0	+1	+2	+3	+4
Symbol

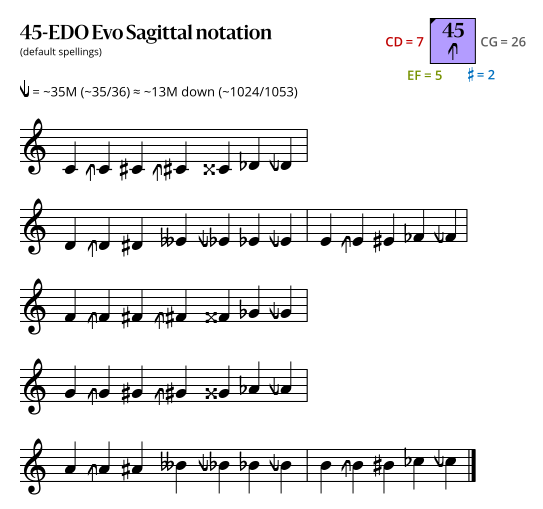
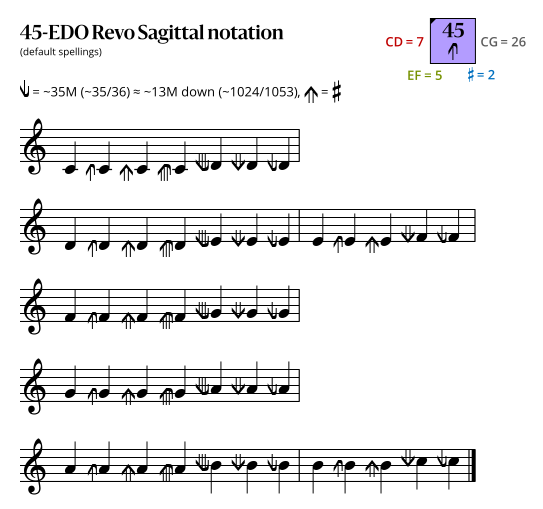
Sagittal notation

This notation uses the same sagittal sequence as EDOs 52 and 59b.

Evo flavor

Revo flavor

Evo-SZ flavor

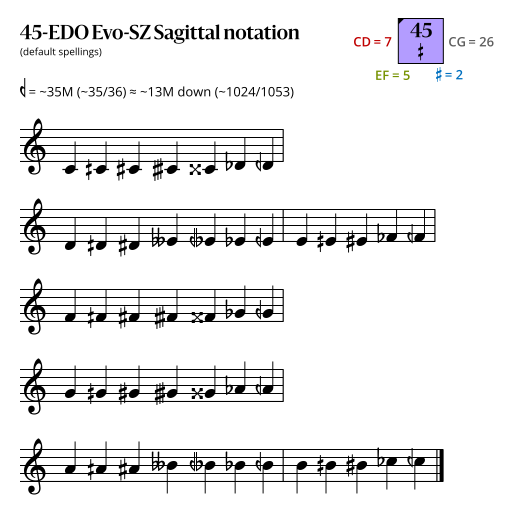
Because it contains no Sagittal symbols, this Evo-SZ Sagittal notation is also a Stein-Zimmerman notation.

In the following diagrams, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's primary comma (the comma it exactly represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it approximately represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this EDO.

Regular temperament properties

Commas

This is a partial list of the commas that 45et tempers out with its patent val, ⟨45 71 104 126 143 156 167].

Prime limit	Ratio^{[note 1]}	Monzo	Cents	Color name	Name(s)
5	81/80	[-4 4 -1⟩	21.51	Gu	Syntonic comma, Didymus comma, meantone comma
5	(26 digits)	[1 -27 18⟩	0.86	Satritribiyo	Ennealimma
7	16807/16384	[-14 0 0 5⟩	44.13	Laquinzo	Cloudy comma
7	525/512	[-9 1 2 1⟩	43.41	Lazoyoyo	Avicennma, Avicenna's enharmonic diesis
7	875/864	[-5 -3 3 1⟩	21.90	Zotrigu	Keema
7	3125/3087	[0 -2 5 -3⟩	21.18	Triru-aquinyo	Gariboh comma
7	(16 digits)	[-11 -9 0 9⟩	1.84	Tritrizo	Septimal ennealimma
7	4375/4374	[-1 -7 4 1⟩	0.40	Zoquadyo	Ragisma
11	45/44	[-2 2 1 0 -1⟩	38.91	Luyo	Undecimal 1/5-tone
11	385/384	[-7 -1 1 1 1⟩	4.50	Lozoyo	Keenanisma
11	(18 digits)	[24 -6 0 1 -5⟩	0.51	Saquinlu-azo	Quartisma

↑ Ratios longer than 10 digits are presented by placeholders with informative hints.

Octave stretch and compression

45edo's approximations of 3/1, 5/1, 7/1, 11/1 and 13/1 and 17/1 are all improved by an stretched-octave version of 45edo, such as 116ed6. The trade-off is a slightly worse 2/1.

The tuning 183ed17 may be used for this purpose too, it improves 3/1, 5/1, 7/1, 11/1, 13/1 and 17/1, but at the cost of a noticeably worse 2/1 than 116ed6.

What follows is a comparison of compressed- and stretched-octave 45edo tunings.

209zpi

Step size: 26.550 ¢, octave size: 1194.8 ¢

Compressing the octave of 45edo by around 5 ¢ results in improved primes 5 and 7, but worse primes 2, 3, 11 and 13. This approximates all harmonics up to 16 within 11.1 ¢. The tuning 209zpi does this.

Approximation of harmonics in 209zpi
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	-5.2	+9.6	-10.5	+1.4	+4.4	+3.0	+10.8	-7.3	-3.8	-9.5	-0.9
Error	Relative (%)	-19.8	+36.3	-39.5	+5.4	+16.6	+11.4	+40.7	-27.3	-14.4	-35.8	-3.2
Step		45	72	90	105	117	127	136	143	150	156	162

Approximation of harmonics in 209zpi (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-6.7	-2.2	+11.1	+5.6	+6.8	-12.5	+0.1	-9.1	+12.7	+11.8	-12.1	-6.1
Error	Relative (%)	-25.2	-8.4	+41.7	+20.9	+25.6	-47.1	+0.3	-34.1	+47.7	+44.4	-45.5	-23.0
Step		167	172	177	181	185	188	192	195	199	202	204	207

45edo

Step size: 26.667 ¢, octave size: 1200.0 ¢

Pure-octaves 45edo approximates all harmonics up to 16 within 13.0 ¢.

Approximation of harmonics in 45edo
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+0.0	-8.6	+0.0	-13.0	-8.6	-8.8	+0.0	+9.4	-13.0	+8.7	-8.6
Error	Relative (%)	+0.0	-32.3	+0.0	-48.7	-32.3	-33.1	+0.0	+35.3	-48.7	+32.6	-32.3
Steps (reduced)		45 (0)	71 (26)	90 (0)	104 (14)	116 (26)	126 (36)	135 (0)	143 (8)	149 (14)	156 (21)	161 (26)

Approximation of harmonics in 45edo (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	+12.8	-8.8	+5.1	+0.0	+1.7	+9.4	-4.2	-13.0	+9.2	+8.7	+11.7	-8.6
Error	Relative (%)	+48.0	-33.1	+19.0	+0.0	+6.4	+35.3	-15.7	-48.7	+34.6	+32.6	+44.0	-32.3
Steps (reduced)		167 (32)	171 (36)	176 (41)	180 (0)	184 (4)	188 (8)	191 (11)	194 (14)	198 (18)	201 (21)	204 (24)	206 (26)

45et, 13-limit WE tuning

Step size: 26.695 ¢, octave size: 1201.3 ¢

Stretching the octave of 45edo by around 1 ¢ results in improved primes 3, 5, 7 and 13, but worse primes 2 and 11. This approximates all harmonics up to 16 within 13.2 ¢. Its 13-limit WE tuning and 13-limit TE tuning both do this.

Approximation of harmonics in 45et, 13-limit WE tuning
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+1.3	-6.6	+2.5	-10.0	-5.3	-5.3	+3.8	-13.2	-8.8	+13.1	-4.1
Error	Relative (%)	+4.8	-24.8	+9.6	-37.6	-20.0	-19.7	+14.3	-49.5	-32.8	+49.1	-15.2
Step		45	71	90	104	116	126	135	142	149	156	161

Approximation of harmonics in 45et, 13-limit WE tuning (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-9.2	-4.0	+10.1	+5.1	+6.9	-11.9	+1.2	-7.5	-11.9	-12.3	-9.2	-2.8
Error	Relative (%)	-34.3	-14.9	+37.7	+19.1	+25.9	-44.7	+4.6	-28.0	-44.4	-46.1	-34.4	-10.4
Step		166	171	176	180	184	187	191	194	197	200	203	206

161ed12

Step size: Octave size: 1202.4 ¢

Stretching the octave of 45edo by around 2.5 ¢ results in improved primes 3, 5, 7 and 13, but worse primes 2 and 11. This approximates all harmonics up to 16 within 12.2 ¢. The tuning 161ed12 does this.

Approximation of harmonics in 161ed12
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+2.4	-4.8	+4.8	-7.4	-2.4	-2.1	+7.2	-9.6	-5.0	-9.7	+0.0
Error	Relative (%)	+9.0	-18.0	+18.0	-27.7	-9.0	-7.8	+27.1	-36.1	-18.7	-36.2	+0.0
Steps (reduced)		45 (45)	71 (71)	90 (90)	104 (104)	116 (116)	126 (126)	135 (135)	142 (142)	149 (149)	155 (155)	161 (0)

Approximation of harmonics in 161ed12 (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-5.0	+0.3	-12.2	+9.6	+11.6	-7.2	+6.0	-2.6	-6.9	-7.3	-4.1	+2.4
Error	Relative (%)	-18.6	+1.2	-45.8	+36.1	+43.3	-27.1	+22.6	-9.7	-25.8	-27.2	-15.2	+9.0
Steps (reduced)		166 (5)	171 (10)	175 (14)	180 (19)	184 (23)	187 (26)	191 (30)	194 (33)	197 (36)	200 (39)	203 (42)	206 (45)

116ed6

Step size: Octave size: 1203.3 ¢

Stretching the octave of 45edo by around 3 ¢ results in improved primes 3, 5, 7, 11 and 13, but a worse prime 2. This approximates all harmonics up to 16 within 13.4 ¢. The tuning 116ed6 does this. So does 126ed7 whose octave is identical within 0.1 ¢.

Approximation of harmonics in 116ed6
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+3.3	-3.3	+6.7	-5.3	+0.0	+0.5	+10.0	-6.7	-1.9	-6.5	+3.3
Error	Relative (%)	+12.5	-12.5	+25.0	-19.6	+0.0	+2.0	+37.5	-25.0	-7.1	-24.2	+12.5
Steps (reduced)		45 (45)	71 (71)	90 (90)	104 (104)	116 (0)	126 (10)	135 (19)	142 (26)	149 (33)	155 (39)	161 (45)

Approximation of harmonics in 116ed6 (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-1.5	+3.9	-8.6	-13.4	-11.4	-3.3	+10.0	+1.4	-2.8	-3.1	+0.1	+6.7
Error	Relative (%)	-5.7	+14.5	-32.1	-50.0	-42.5	-12.5	+37.5	+5.4	-10.5	-11.7	+0.5	+25.0
Steps (reduced)		166 (50)	171 (55)	175 (59)	179 (63)	183 (67)	187 (71)	191 (75)	194 (78)	197 (81)	200 (84)	203 (87)	206 (90)

45et, 7-limit WE tuning

Step size: 26.745 ¢, octave size: 1203.5 ¢

Stretching the octave of 45edo by around 3.5 ¢ results in improved primes 3, 5, 7, 11 and 13, but a worse prime 2. This approximates all harmonics up to 16 within 12.6 ¢. Its 7-limit WE tuning and 7-limit TE tuning both do this.

Approximation of harmonics in 45et, 7-limit WE tuning
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+3.5	-3.1	+7.1	-4.8	+0.5	+1.0	+10.6	-6.1	-1.3	-5.8	+4.0
Error	Relative (%)	+13.2	-11.4	+26.4	-18.1	+1.7	+3.9	+39.5	-22.9	-4.9	-21.8	+14.9
Step		45	71	90	104	116	126	135	142	149	155	161

Approximation of harmonics in 45et, 7-limit WE tuning (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-0.9	+4.6	-7.9	-12.6	-10.6	-2.6	+10.8	+2.2	-2.0	-2.3	+1.0	+7.5
Error	Relative (%)	-3.2	+17.1	-29.5	-47.3	-39.7	-9.7	+40.3	+8.3	-7.5	-8.7	+3.6	+28.1
Step		166	171	175	179	183	187	191	194	197	200	203	206

207zpi

Step size: 26.762 ¢, octave size: 1204.3 ¢

Stretching the octave of 45edo by around 4 ¢ results in improved primes 3, 5, 7, 11 and 13, but a worse prime 2. This approximates all harmonics up to 16 within 12.9 ¢. The tuning 207zpi does this.

Approximation of harmonics in 207zpi
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+4.3	-1.9	+8.6	-3.1	+2.4	+3.2	+12.9	-3.7	+1.2	-3.2	+6.7
Error	Relative (%)	+16.0	-6.9	+32.1	-11.5	+9.1	+11.9	+48.1	-13.8	+4.6	-12.0	+25.1
Step		45	71	90	104	116	126	135	142	149	155	161

Approximation of harmonics in 207zpi (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	+2.0	+7.5	-4.9	-9.6	-7.5	+0.6	-12.7	+5.5	+1.3	+1.1	+4.4	+11.0
Error	Relative (%)	+7.3	+27.9	-18.4	-35.9	-28.1	+2.2	-47.6	+20.6	+5.0	+4.0	+16.5	+41.2
Step		166	171	175	179	183	187	190	194	197	200	203	206

71edt

Step size: 26.788 ¢, octave size: 1205.5 ¢

Stretching the octave of 45edo by around 5.5 ¢ results in improved primes 3, 5, 7, 11 and 13, but a worse prime 2. This approximates all harmonics up to 16 within 11.9 ¢. The tuning 71edt does this. So do the tunings 104ed5 and 155ed11 whose octave is identical within 0.3 ¢.

Approximation of harmonics in 71edt
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+5.5	+0.0	+10.9	-0.4	+5.5	+6.5	-10.4	+0.0	+5.1	+0.8	+10.9
Error	Relative (%)	+20.4	+0.0	+40.8	-1.3	+20.4	+24.2	-38.8	+0.0	+19.1	+3.1	+40.8
Steps (reduced)		45 (45)	71 (0)	90 (19)	104 (33)	116 (45)	126 (55)	134 (63)	142 (0)	149 (7)	155 (13)	161 (19)

Approximation of harmonics in 71edt (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	+6.3	+11.9	-0.4	-4.9	-2.7	+5.5	-7.8	+10.6	+6.5	+6.3	+9.7	-10.4
Error	Relative (%)	+23.5	+44.6	-1.3	-18.4	-10.2	+20.4	-29.0	+39.5	+24.2	+23.5	+36.2	-38.8
Steps (reduced)		166 (24)	171 (29)	175 (33)	179 (37)	183 (41)	187 (45)	190 (48)	194 (52)	197 (55)	200 (58)	203 (61)	205 (63)

183ed17

Octave size: 1206.1 ¢

Stretching the octave of 45edo by around 6 ¢ results in improved primes 3, 5, 7, 11, 13 and 17, but a worse prime 2. This approximates all harmonics up to 16 within 13.3 ¢. The tuning 183ed17 does this.

Approximation of harmonics in 183ed17
Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+6.1	+1.1	+12.3	+1.2	+7.2	+8.4	-8.4	+2.1	+7.3	+3.2	+13.3
Error	Relative (%)	+22.9	+4.0	+45.8	+4.5	+26.9	+31.2	-31.3	+7.9	+27.4	+11.8	+49.7
Steps (reduced)		45 (45)	71 (71)	90 (90)	104 (104)	116 (116)	126 (126)	134 (134)	142 (142)	149 (149)	155 (155)	161 (161)

Approximation of harmonics in 183ed17 (continued)
Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	+8.8	-12.3	+2.3	-2.3	+0.0	+8.3	-4.9	-13.3	+9.4	+9.3	+12.7	-7.3
Error	Relative (%)	+32.7	-45.9	+8.4	-8.4	+0.0	+30.8	-18.4	-49.7	+35.1	+34.7	+47.5	-27.4
Steps (reduced)		166 (166)	170 (170)	175 (175)	179 (179)	183 (0)	187 (4)	190 (7)	193 (10)	197 (14)	200 (17)	203 (20)	205 (22)

Instruments

Lumatone

See Lumatone mapping for 45edo

Music

Bryan Deister

(short clip) Fantasy in 45edo (2025)

JUMBLE

[1] Ratios longer than 10 digits are presented by placeholders with informative hints.

[note 1]

45edo

Contents