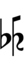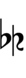51edo

← 50edo

51edo

52edo →

Prime factorization	3 × 17
Step size	23.5294 ¢
Fifth	30\51 (705.882 ¢) (→ 10\17)
Semitones (A1:m2)	6:3 (141.2 ¢ : 70.59 ¢)
Consistency limit	3
Distinct consistency limit	3

Theory

51 = 3 × 17, and 51edo shares its fifth with 17edo.

Using the patent val, 51et tempers out 250/243 in the 5-limit, 225/224 and 2401/2400 in the 7-limit, and 55/54 and 100/99 in the 11-limit. It is the optimal patent val for sonic, the rank-3 temperament tempering out 55/54, 100/99, and 250/243, and also for the rank-4 temperament tempering out 55/54. It provides an alternative tuning to 22edo for porcupine, with a nice fifth but a rather flat major third, and the optimal patent val for the 7- and 11-limit porky temperament, which is sonic plus 225/224. 51 contains an archeotonic 6L 1s scale based on repetitions of 8\51, creating a scale with a whole-tone-like drive towards the tonic through the 17edo semitone at the top.

Alternatively, using the 51c val ⟨51 81 119 143], the 5/4 is mapped to 1\3 (400 cents), supporting augmented. In the 7-limit it tempers out 245/243 and supports hemiaug and rodan. The 51cd val ⟨51 81 119 144] takes the same 7/4 from 17edo, and supports augene.

51edo's step is the closest direct approximation to the Pythagorean comma by edo steps, though that comma itself is mapped to a different interval.

Odd harmonics

Approximation of prime harmonics in 51edo

Harmonic		2	3	5	7	11	13	17	19	23	29	31
Error	Absolute (¢)	+0.0	+3.9	-9.8	-4.1	-10.1	+6.5	-10.8	+8.4	+7.0	+5.7	+7.9
	Relative (%)	+0.0	+16.7	-41.8	-17.5	-43.1	+27.8	-46.1	+35.6	+29.8	+24.3	+33.6
Steps (reduced)		51 (0)	81 (30)	118 (16)	143 (41)	176 (23)	189 (36)	208 (4)	217 (13)	231 (27)	248 (44)	253 (49)

Subsets and supersets

51edo contains 3edo and 17edo as subsets. A step of 51edo is exactly 12 skismas.

Intervals

Degrees	Cents	Ups and downs notation
0	0.000	Perfect 1sn	P1	D
1	23.529	Up 1sn	^1	^D
2	47.059	Downminor 2nd	vm2	vEb
3	70.588	Minor 2nd	m2	Eb
4	94.118	Upminor 2nd	^m2	^Eb
5	117.647	Downmid 2nd	v~2	^^Eb
6	141.176	Mid 2nd	~2	vvvE, ^^^Eb
7	164.706	Upmid 2nd	^~2	vvE
8	188.235	Downmajor 2nd	vM2	vE
9	211.765	Major 2nd	M2	E
10	235.294	Upmajor 2nd	^M2	^E
11	258.824	Downminor 3rd	vm3	vF
12	282.353	Minor 3rd	m3	F
13	305.882	Upminor 3rd	^m3	^F
14	329.412	Downmid 3rd	v~3	^^F
15	352.941	Mid 3rd	~3	^^^F, vvvF#
16	376.471	Upmid 3rd	^~3	vvF#
17	400.000	Downmajor 3rd	vM3	vF#
18	423.529	Major 3rd	M3	F#
19	447.509	Upmajor 3rd	^M3	^F#
20	470.588	Down 4th	v4	vG
21	494.118	Perfect 4th	P4	G
22	517.647	Up 4th	^4	^G
23	541.176	Downdim 5th	vd5	vAb
24	564.706	Dim 5th	d5	Ab
25	588.235	Updim 5th	^d5	^Ab
26	611.765	Downaug 4th	vA4	vG#
27	635.294	Aug 4th	A4	G#
28	658.824	Upaug 4th	^A4	^G#
29	682.353	Down 5th	v5	vA
30	705.882	Perfect 5th	P5	A
31	729.412	Up 5th	^5	^A
32	752.941	Downminor 6th	vm6	vBb
33	776.471	Minor 6th	m6	Bb
34	800.000	Upminor 6th	^m6	^Bb
35	823.529	Downmid 6th	v~6	^^Bb
36	847.059	Mid 6th	~6	vvvB, ^^^Bb
37	870.588	Upmid 6th	^~6	vvB
38	894.118	Downmajor 6th	vM6	vB
39	917.647	Major 6th	M6	B
40	941.176	Upmajor 6th	^M6	^B
41	964.706	Downminor 7th	vm7	vC
42	988.235	Minor 7th	m7	C
43	1011.765	Upminor 7th	^m7	^C
44	1035.294	Downmid 7th	v~7	^^C
45	1058.824	Mid 7th	~7	^^^C, vvvC#
46	1082.353	Upmid 7th	^~7	vvC#
47	1105.882	Downmajor 7th	vM7	vC#
48	1129.412	Major 7th	M7	C#
49	1152.941	Upmajor 7th	^M7	^C#
50	1176.471	Down 8ve	v8	vD
51	1200.000	Perfect 8ve	P8	D

Notation

Ups and downs notation

In 51edo, a sharp raises by six steps, so a combination of quarter tone accidentals and arrow accidentals from Helmholtz–Ellis notation can be used to fill in the gaps.

Step offset	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Sharp symbol
Flat symbol

If double arrows are not desirable, then arrows can be attached to quarter-tone accidentals:

Step offset	0	1	2	3	4	5	6	7	8	9	10	11	12	13
Sharp symbol
Flat symbol

Ivan Wyschnegradsky's notation

Since a sharp raises by six steps, Wyschnegradsky accidentals borrowed from 72edo can also be used:

Step offset	0	1	2	3	4	5	6	7	8	9	10	11	12	13
Sharp symbol
Flat symbol

Sagittal notation

In the following diagrams, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's primary comma (the comma it exactly represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it approximately represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this edo.

Evo flavor

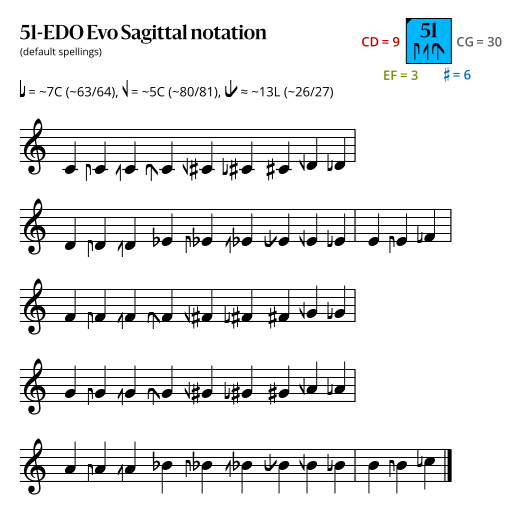
Revo flavor

Evo-SZ flavor

Regular temperament properties

Subgroup	Comma list	Mapping	Optimal 8ve stretch (¢)	Tuning error
				Absolute (¢)	Relative (%)
2.3.7	1029/1024, [17 -16 3⟩	[⟨51 81 143]]	−0.339	1.63	6.92
2.3.5	128/125, [-13 17 -6⟩	[⟨51 81 119]] (51c)	−2.789	2.41	10.3
2.3.5	250/243, 34171875/33554432	[⟨51 81 118]] (51)	+0.581	2.77	11.8

Rank-2 temperaments

Table of rank-2 temperaments by generator

Periods per 8ve	Generator*	Cents*	Associated ratio*	Temperament
1	5\51	117.6	15/14	Miracle (51e, out of tune) / oracle (51)
1	7\51	164.7	11/10	Porky (51)
1	10\51	235.3	8/7	Rodan (51cf…, out of tune) / aerodino (51ce)
1	5\51	541.2	15/11	Necromanteion (51ce)
3	19\51 (2\51)	447.1 (47.1)	9/7 (36/35)	Hemiaug (51ce)
3	21\51 (4\51)	494.1 (94.1)	4/3 (16/15)	Augmented (51c)

* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct

Scales

• Porky[7], Palace: 7 7 7 9 7 7 7
• UFO scale (inflected MOS of Teefs[19]): 2 2 4 1 2 2 2 4 2 5 2 4 4 2 2 1 4 2 2
• Cosmic scale (subset of UFO scale): 21 9 4 9 8

Instruments

Lumatone

See Lumatone mapping for 51edo.

Music

Frédéric Gagné

• Whalectric (2022) – YouTube | score – 7:4 semiquartal 4|4 mode

James Mulvale (FASTFAST)

• STARS (Thoughts and Prayers) (2020)

Ray Perlner

• Fugue (2023) – for organ in 51edo Porcupine[7] ssssssL "Pandian"