Revision as of 00:00, 17 July 2018

26edo divides the octave into 26 equal parts of 46.154 cents each. It tempers out 81/80 in the 5-limit, making it a meantone tuning with a very flat fifth. In the 7-limit, it tempers out 50/49, 525/512 and 875/864, and supports injera, flattone, lemba and doublewide temperaments. It really comes into its own as a higher-limit temperament, being the smallest equal division which represents the 13 odd limit consistently. 26edo has a very good approximation of the harmonic seventh (7/4).

26edo's "minor sixth" is very close to phi (i. e., the golden ratio).

Structure

The structure of 26edo is an interesting beast, with various approaches relating it to various rank two temperaments.

1. In terms of more traditional chord types we have flattone, a variant of meantone with flat fifths, which yields interesting but to some unsatisfying results (due mainly to the dissonance of its thirds, and its major seconds of either approximately 10/9 or 8/7, but NOT 9/8).

2. As two chains of meantone fifths half an octave apart, it supports injera temperament. The generator for this is an interval which can be called either 21/20 or 15/14, and which represents two steps of 26, and hence one step of 13. Hence in 26edo (as opposed to, for instance, 38edo) it can be viewed as two parallel 13edo scales, and from that point of view we can consider it as supporting the 13b&26 temperament, allowing the two chains be shifted slightly and which can be used for more atonal melodies. In this way its internal dynamics resemble those of 14edo.

3. 26edo nearly perfectly approximates the 7th and 11th harmonics, and an entire system may be constructed analogous to that based on the 3rd and 5th harmonics. In terms of subgroups, this is the 2.7.11 subgroup, and on this 26 tempers out the pair of commas 65536/65219 and | -3 0 0 6 -4>. The 65536/65219 comma, the orgonisma, leads to orgone temperament with an approximate 77/64 generator of 7\26, with MOS scales of size 7, 11 and 15. The | -3 0 0 6 -4> comma leads to a half-octave period and an approximate 49/44 generator of 4\26, leading to MOS of size 8 and 14.

4. We can also treat 26-EDO as a full 13-limit temperament, since it is consistent on the 13-limit (unlike all lower EDOs).

5. It also has a pretty good 17th harmonic and tempers out the comma 459:448, thus three fifths gives a 17:14 and four gives a 21:17; "mushtone". Mushtone is high in badness, but 26edo does it pretty well (and 33edo even better). Because 26edo also tempers out 85:84, the septendecimal major and minor thirds are equivalent to their pental counterparts, making mushtone the same as flattone.

Intervals

Degrees	Size in cents	Approximate Ratios*	Solfege	Interval Name	Example in D
0	0.00	1/1	do	P1	D
1	46.15	33/32, 49/48, 36/35, 25/24	di	A1	D#
2	92.31	21/20, 22/21, 26/25	rih	d2	Ebb
3	138.46	12/11, 13/12, 14/13, 16/15	ru	m2	Eb
4	184.62	9/8, 10/9, 11/10	re	M2	E
5	230.77	8/7, 15/13	ri	A2	E#
6	276.92	7/6, 13/11, 33/28	ma	d3	Fb
7	323.08	6/5	me	m3	F
8	369.23	5/4, 11/9, 16/13	muh/mi	M3	F#
9	415.38	9/7, 14/11, 33/26	maa	A3	Fx
10	461.54	21/16, 13/10	fe	d4	Gb
11	507.69	4/3	fa	P4	G
12	553.85	11/8, 18/13	fu	A4	G#
13	600.00	7/5, 10/7	fi/se	AA4, dd5	Gx, Abb
14	646.15	16/11, 13/9	su	d5	Ab
15	692.31	3/2	sol	P5	A
16	738.46	32/21, 20/13	si	A5	A#
17	784.62	11/7, 14/9	leh	d6	Bbb
18	830.77	13/8, 8/5	le/lu	m6	Bb
19	876.92	5/3	la	M6	B
20	923.08	12/7, 22/13	li	A6	B#
21	969.23	7/4	ta	d7	Cb
22	1015.38	9/5, 16/9, 20/11	te	m7	C
23	1061.54	11/6, 13/7, 15/8, 24/13	tu/ti	M7	C#
24	1107.69	21/11, 25/13, 40/21	to	A7	Cx
25	1153.85	64/33, 96/49, 35/18, 48/25	da	d8	Db
26	1200.00	2/1	do	P8	D

based on treating 26-EDO as a 13-limit temperament; other approaches are possible.

Using color notation, qualities can be loosely associated with colors:

quality	color	monzo format	examples
diminished	blue	{a, b, 0, 1}	7/6, 7/4
minor	fourthward white	{a, b}, b < -1	32/27, 16/9
"	green	{a, b, -1}	6/5, 9/5
major	yellow	{a, b, 1}	5/4, 5/3
"	fifthward white	{a, b}, b > 1	9/8, 27/16
augmented	red	{a, b, 0, -1}	9/7, 12/7

All 26edo chords can be named using conventional methods, expanded to include augmented and diminished 2nd, 3rds, 6ths and 7ths. Spelling certain chords properly may require triple sharps and flats, especially if the tonic is anything other than the 11 keys in the Eb-C# range. Here are the blue, green, yellow and red triads

color of the 3rd	JI chord	notes as edosteps	notes of C chord	written name	spoken name
blue	6:7:9	0-6-15	C Ebb G	C(b3) or C(d3)	C flat-three or C dim-three
green	10:12:15	0-7-15	C Eb G	Cm	C minor
yellow	4:5:6	0-8-15	C E G	C	C major or C
red	14:18:27	0-9-15	C E# G	C(#3) or C(A3)	C sharp-three or C aug-three

For a more complete list, see Ups and Downs Notation - Chord names in other EDOs.

Selected just intervals by error

The following table shows how some prominent just intervals are represented in 26edo (ordered by absolute error).

Interval, complement	Error (abs., in cents)
13/12, 24/13	0.111
8/7, 7/4	0.405
14/11, 11/7	2.123
10/9, 9/5	2.212
11/8, 16/11	2.528
13/10, 20/13	7.325
6/5, 5/3	7.436
18/13, 13/9	9.536
4/3, 3/2	9.647
16/13, 13/8	9.758
7/6, 12/7	10.052
14/13, 13/7	10.163
12/11, 11/6	12.176
13/11, 22/13	12.287
15/11, 22/15	16.895
15/13, 26/15	16.972
5/4, 8/5	17.083
7/5, 10/7	17.488
15/14, 28/15	19.019
9/8, 16/9	19.295
16/15, 15/8	19.424
11/10, 20/11	19.611
9/7, 14/9	19.699
11/9, 18/11	21.823

Rank two temperaments

List of 26et rank two temperaments by badness

List of edo-distinct 26et rank two temperaments

Periods per octave	Generator	Temperaments
1	1\26	Quartonic/Quarto
1	3\26	Jerome/Bleu/Secund
1	5\26	Cynder/Mothra
1	7\26	Superkleismic/Orgone/Shibboleth
1	9\26	Roman/Wesley
1	11\26	Meantone/Flattone
2	1\26	Elvis
2	2\26	Injera
2	3\26	Fifive/Crepuscular
2	4\26	Unidec/Hendec/Dubbla
2	5\26	Lemba
2	6\26	Doublewide/Cavalier
13	1\26	Triskaidekic

Hendec in 26et

Hendec, the 13-limit 26&46 temperament with generator ~10/9, concentrates the intervals of greatest accuracy in 26et into the lower ranges of complexity. It has a period of half an octave, with 13/12 reachable by four generators, 8/7 by two, 14/11 by one, 10/9 by one, and 11/8 by three. All of these are tuned to within 2.5 cents of accuracy.

Commas

26et tempers out the following commas. (Note: This assumes the val < 26 41 60 73 90 96 |.)

Ratio	Monzo	Size (Cents)	Name 1	Name 2	Name 3
81/80	\| -4 4 -1 >	21.51	Syntonic Comma	Didymos Comma	Meantone Comma
5696703/5695946	\| -17 62 -35 >	0.23	Senior
525/512	\| -9 1 2 1 >	43.41	Avicennma	Avicenna's Enharmonic Diesis
50/49	\| 1 0 2 -2 >	34.98	Tritonic Diesis	Jubilisma
875/864	\| -5 -3 3 1 >	21.90	Keema
4000/3969	\| 5 -4 3 -2 >	13.47	Octagar
1728/1715	\| 6 3 -1 -3 >	13.07	Orwellisma	Orwell Comma
1029/1024	\| -10 1 0 3 >	8.43	Gamelisma
321489/320000	\| -9 8 -4 2 >	8.04	Varunisma
1065875/1063543	\| -26 -1 1 9 >	3.79	Wadisma
4375/4374	\| -1 -7 4 1 >	0.40	Ragisma
99/98	\| -1 2 0 -2 1 >	17.58	Mothwellsma
100/99	\| 2 -2 2 0 -1 >	17.40	Ptolemisma
105/104	\| -3 1 1 1 0 -1 >	16.57	Animist
65536/65219	\| 16 0 0 -2 -3 >	8.39	Orgonisma
385/384	\| -7 -1 1 1 1 >	4.50	Keenanisma
441/440	\| -3 2 -1 2 -1 >	3.93	Werckisma
3025/3024	\| -4 -3 2 -1 2 >	0.57	Lehmerisma
9801/9800	\| -3 4 -2 -2 2 >	0.18	Kalisma	Gauss' Comma

Orgone Temperament

Andrew Heathwaite first proposed orgone temperament to take advantage of 26edo's excellent 11 and 7 approximations. 7 degrees of 26edo is a wide minor third of approximately 323.077 cents, and that interval taken as a generator produces 7-tone and 11-tone MOS scales:

The 7-tone scale in degrees-in-between: 5 2 5 2 5 2 5. MOS of type 4L 3s (mish).

The 7-tone scale in cents: 0 231 323 554 646 877 969 1200.

The 11-tone scale in degrees-in-between: 2 3 2 2 3 2 3 2 2 3 2. MOS of type 4L 7s.

The 11-tone scale in cents: 0 92 231 323 415 554 646 785 877 969 1108 1200.

The primary triad for orgone temperament is 8:11:14 and its subharmonic inversion, which these scales have in abundance. 2g approximates 16:11 and 3g approximates 7:4 (and I would call that the definition of Orgone Temperament). That also implies that g approximates the difference between 7:4 and 16:11, which is 77:64, about 320.1 cents.

37edo is another orgone tuning, and 89edo is better even than 26. If we take 11 and 26 to be the edges of the Orgone Spectrum, we may fill in the rest of the spectrum thus:

3\11
				19\70
			16\59
				29\107
		13\48
				36\133
			23\85
				33\122
	10\37
				37\137
			27\100
				44\163
		17\63
				41\152
			24\89
				31\115
7\26

Orgone has a minimax tuning which sharpens both 7 and 11 by 1/5 of an orgonisma, or 1.679 cents. This makes the generator g a 77/64 sharp by 2/5 of the orgonisma. From this we may conclude that 24/89 or 31/115 would be reasonable alternatives to the 7/26 generator.

Additional Scalar Bases Available in 26-EDO:

Since the perfect 5th in 26-EDO spans 15 degrees, it can be divided into three equal parts (each approximately an 8/7) as well as five equal parts (each approximately a 13/12). The former approach produces MOS at 1L+4s, 5L+1s, and 5L+6s (5 5 5 5 6, 5 5 5 5 5 1, and 4 1 4 1 4 1 4 1 4 1 1 respectively), and is excellent for 4:6:7 triads. The latter produces MOS at 1L+7s and 8L+1s (3 3 3 3 3 3 3 5 and 3 3 3 3 3 3 3 3 2 respectively), and is fairly well-supplied with 4:6:7:11:13 pentads. It also works well for more conventional (though further from Just) 6:7:9 triads, as well as 4:5:6 triads that use the worse mapping for 5 (making 5/4 the 415.38-cent interval).

-Igs

Literature

Sword, Ron. **Icosihexaphonic Scales for Guitar**. IAAA Press. 2010 - A Guitar-scale thesaurus for 26-EDO.

Compositions

Canon 3-in-1 on a ground ‘The tempest’, by Claudi Meneghin

A Time-Yellowed Photo of the Cliffs Hangs on the Wall by Igliashon Jones

Two Pairs of Socks by Igliashon Jones

Etude in 26-tone equal temperament play by Herman Miller

under the heatDome play by Jon Lyle Smith

A New Recording of Organ Study #1 play by Daniel Thompson

Little Fugue in 26 by Cameron Bobro

26 tone fugue (unfinished) by Peter Kosmorsky (based on the melody he was singing in the shower, in orgone, to the presumed confusion of those in earshot)

Microtonal music in 26-EDO by Shaahin Mohajeri

Chiapas Palenque by Zach Curley

Injera Jam by Zach Curley

Guitar Serenade in Q Major by Zach Curley

Public Rituals « Jim Aikin's Oblong Blob “The Triumphal Procession of Nebuchadnezzar“

Melopœia Project – 26 EDO album based on Tolkein’s Silmarillion – Ainulindalë – Unfretted

Morpheous Wing in 26 edo by Chris Vaisvil

26edo: Difference between revisions

Revision as of 00:00, 17 July 2018

Contents

Structure

Intervals

Selected just intervals by error

Rank two temperaments

Hendec in 26et

Commas

Orgone Temperament

Additional Scalar Bases Available in 26-EDO:

Literature

Compositions

Navigation menu

@@ Line 1: / Line 1: @@
-<h2>IMPORTED REVISION FROM WIKISPACES</h2>
+__FORCETOC__
-This is an imported revision from Wikispaces. The revision metadata is included below for reference:<br>
+''26edo'' divides the [[Octave|octave]] into 26 equal parts of 46.154 [[cent|cent]]s each. It tempers out 81/80 in the [[5-limit|5-limit]], making it a meantone tuning with a very flat fifth. In the [[7-limit|7-limit]], it tempers out 50/49, 525/512 and 875/864, and supports [[Meantone_family|injera]], [[Meantone_family|flattone]], [[Jubilismic_clan#Lemba|lemba]] and [[Jubilismic_clan#Doublewide|doublewide]] temperaments. It really comes into its own as a higher-limit temperament, being the smallest equal division which represents the [[13-limit|13 odd limit]] [[consistent|consistently]]. 26edo has a very good approximation of the harmonic seventh ([[7/4|7/4]]).
-: This revision was by author [[User:TallKite|TallKite]] and made on <tt>2017-11-11 19:01:32 UTC</tt>.<br>
-: The original revision id was <tt>621461935</tt>.<br>
-: The revision comment was: <tt></tt><br>
-The revision contents are below, presented both in the original Wikispaces Wikitext format, and in HTML exactly as Wikispaces rendered it.<br>
-<h4>Original Wikitext content:</h4>
-<div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;white-space: pre-wrap ! important" class="old-revision-html">[[toc]]
-//26edo// divides the [[octave]] into 26 equal parts of 46.154 [[cent]]s each. It tempers out 81/80 in the [[5-limit]], making it a meantone tuning with a very flat fifth. In the [[7-limit]], it tempers out 50/49, 525/512 and 875/864, and supports [[Meantone family|injera]], [[Meantone family|flattone]], [[Jubilismic clan#Lemba|lemba]] and [[Jubilismic clan#Doublewide|doublewide]] temperaments. It really comes into its own as a higher-limit temperament, being the smallest equal division which represents the [[13-limit|13 odd limit]] [[consistent|consistently]]. 26edo has a very good approximation of the harmonic seventh ([[7_4|7/4]]).
 edo's "minor sixth" is very close to phi (i. e., the golden ratio).
 ==Structure==
 The structure of 26edo is an interesting beast, with various approaches relating it to various rank two temperaments.
-. In terms of more traditional chord types we have flattone, a variant of meantone with flat fifths, which yields interesting but to some unsatisfying results (due mainly to the dissonance of its thirds, and its major seconds of either approximately [[10_9|10/9]] or [[8_7|8/7]], but NOT [[9_8|9/8]]).
+. In terms of more traditional chord types we have flattone, a variant of meantone with flat fifths, which yields interesting but to some unsatisfying results (due mainly to the dissonance of its thirds, and its major seconds of either approximately [[10/9|10/9]] or [[8/7|8/7]], but NOT [[9/8|9/8]]).
 . As two chains of meantone fifths half an octave apart, it supports injera temperament. The generator for this is an interval which can be called either 21/20 or 15/14, and which represents two steps of 26, and hence one step of 13. Hence in 26edo (as opposed to, for instance, 38edo) it can be viewed as two parallel 13edo scales, and from that point of view we can consider it as supporting the 13b&amp;26 temperament, allowing the two chains be shifted slightly and which can be used for more atonal melodies. In this way its internal dynamics resemble those of 14edo.
 . 26edo nearly perfectly approximates the 7th and 11th harmonics, and an entire system may be constructed analogous to that based on the 3rd and 5th harmonics. In terms of subgroups, this is the 2.7.11 subgroup, and on this 26 tempers out the pair of commas 65536/65219 and | -3 0 0 6 -4&gt;. The 65536/65219 comma, the orgonisma, leads to [[Orgonia|orgone temperament]] with an approximate 77/64 generator of 7\26, with MOS scales of size 7, 11 and 15. The | -3 0 0 6 -4&gt; comma leads to a half-octave period and an approximate 49/44 generator of 4\26, leading to MOS of size 8 and 14.
 . We can also treat 26-EDO as a full 13-limit temperament, since it is consistent on the 13-limit (unlike all lower EDOs).
-. It also has a pretty good 17th harmonic and tempers out the comma 459:448, thus three fifths gives a 17:14 and four gives a 21:17; "mushtone". Mushtone is high in badness, but 26edo does it pretty well (and [[33edo]] even better). Because 26edo also tempers out 85:84, the septendecimal major and minor thirds are equivalent to their pental counterparts, making mushtone the same as flattone.
-==Intervals==
+. It also has a pretty good 17th harmonic and tempers out the comma 459:448, thus three fifths gives a 17:14 and four gives a 21:17; "mushtone". Mushtone is high in badness, but 26edo does it pretty well (and [[33edo|33edo]] even better). Because 26edo also tempers out 85:84, the septendecimal major and minor thirds are equivalent to their pental counterparts, making mushtone the same as flattone.
-||~ Degrees ||~ Size in
-[[cent|cents]] ||~ Approximate Ratios* ||~ Solfege ||~ Interval
+==Intervals==
-Name ||~ Example
-in D ||
+{| class="wikitable"
-||= 0 ||= 0&lt;span style="color: #ffffff;"&gt;.00&lt;/span&gt; ||= 1/1 ||= do ||= P1 ||= D ||
+|-
-||= 1 ||= 46.15 ||= [[33_32|33/32]], [[49_48|49/48]], [[36_35|36/35]], [[25_24|25/24]] ||= di ||= A1 ||= D# ||
+! | Degrees
-||= 2 ||= 92.31 ||= [[21_20|21/20]], [[22_21|22/21]], [[26_25|26/25]] ||= rih ||= d2 ||= Ebb ||
+! | Size in
-||= 3 ||= 138.46 ||= [[12_11|12/11]], [[13_12|13/12]], [[14_13|14/13]], [[16_15|16/15]] ||= ru ||= m2 ||= Eb ||
-||= 4 ||= 184.62 ||= [[9_8|9/8]], [[10_9|10/9]], [[11_10|11/10]] ||= re ||= M2 ||= E ||
+[[cent|cents]]
-||= 5 ||= 230.77 ||= [[8_7|8/7]], 15/13 ||= ri ||= A2 ||= E# ||
+! | Approximate Ratios*
-||= 6 ||= 276.92 ||= [[7_6|7/6]], [[13_11|13/11]], [[33_28|33/28]] ||= ma ||= d3 ||= Fb ||
+! | Solfege
-||= 7 ||= 323.08 ||= [[6_5|6/5]] ||= me ||= m3 ||= F ||
+! | Interval
-||= 8 ||= 369.23 ||= [[5_4|5/4]], [[11_9|11/9]], [[16_13|16/13]] ||= muh/mi ||= M3 ||= F# ||
-||= 9 ||= 415.38 ||= [[9_7|9/7]], [[14_11|14/11]], [[33_26|33/26]] ||= maa ||= A3 ||= Fx ||
+Name
-||= 10 ||= 461.54 ||= [[21_16|21/16]], [[13_10|13/10]] ||= fe ||= d4 ||= Gb ||
+! | Example
-||= 11 ||= 507.69 ||= [[4_3|4/3]] ||= fa ||= P4 ||= G ||
-||= 12 ||= 553.85 ||= [[11_8|11/8]], [[18_13|18/13]] ||= fu ||= A4 ||= G# ||
+in D
-||= 13 ||= 600&lt;span style="color: #ffffff;"&gt;.00&lt;/span&gt; ||= [[7_5|7/5]], [[10_7|10/7]] ||= fi/se ||= AA4, dd5 ||= Gx, Abb ||
+|-
-||= 14 ||= 646.15 ||= [[16_11|16/11]], [[13_9|13/9]] ||= su ||= d5 ||= Ab ||
+| style="text-align:center;" | 0
-||= 15 ||= 692.31 ||= [[3_2|3/2]] ||= sol ||= P5 ||= A ||
+| style="text-align:center;" | 0<span style="color: #ffffff;">.00</span>
-||= 16 ||= 738.46 ||= [[32_21|32/21]], [[20_13|20/13]] ||= si ||= A5 ||= A# ||
+| style="text-align:center;" | 1/1
-||= 17 ||= 784.62 ||= [[11_7|11/7]], [[14_9|14/9]] ||= leh ||= d6 ||= Bbb ||
+| style="text-align:center;" | do
-||= 18 ||= 830.77 ||= [[13_8|13/8]], [[8_5|8/5]] ||= le/lu ||= m6 ||= Bb ||
+| style="text-align:center;" | P1
-||= 19 ||= 876.92 ||= [[5_3|5/3]] ||= la ||= M6 ||= B ||
+| style="text-align:center;" | D
-||= 20 ||= 923.08 ||= [[12_7|12/7]], [[22_13|22/13]] ||= li ||= A6 ||= B# ||
+|-
-||= 21 ||= 969.23 ||= [[7_4|7/4]] ||= ta ||= d7 ||= Cb ||
+| style="text-align:center;" | 1
-||= 22 ||= 1015.38 ||= [[9_5|9/5]], [[16_9|16/9]], [[20_11|20/11]] ||= te ||= m7 ||= C ||
+| style="text-align:center;" | 46.15
-||= 23 ||= 1061.54 ||= [[11_6|11/6]], [[13_7|13/7]], [[15_8|15/8]], [[24_13|24/13]] ||= tu/ti ||= M7 ||= C# ||
+| style="text-align:center;" | [[33/32|33/32]], [[49/48|49/48]], [[36/35|36/35]], [[25/24|25/24]]
-||= 24 ||= 1107.69 ||= [[21_11|21/11]], [[25_13|25/13]], [[40_21|40/21]] ||= to ||= A7 ||= Cx ||
+| style="text-align:center;" | di
-||= 25 ||= 1153.85 ||= [[64_33|64/33]], [[96_49|96/49]], [[35_18|35/18]], [[48_25|48/25]] ||= da ||= d8 ||= Db ||
+| style="text-align:center;" | A1
-||= 26 ||= 1200&lt;span style="color: #ffffff;"&gt;.00&lt;/span&gt; ||= 2/1 ||= do ||= P8 ||= D ||
+| style="text-align:center;" | D#
+|-
+| style="text-align:center;" | 2
+| style="text-align:center;" | 92.31
+| style="text-align:center;" | [[21/20|21/20]], [[22/21|22/21]], [[26/25|26/25]]
+| style="text-align:center;" | rih
+| style="text-align:center;" | d2
+| style="text-align:center;" | Ebb
+|-
+| style="text-align:center;" | 3
+| style="text-align:center;" | 138.46
+| style="text-align:center;" | [[12/11|12/11]], [[13/12|13/12]], [[14/13|14/13]], [[16/15|16/15]]
+| style="text-align:center;" | ru
+| style="text-align:center;" | m2
+| style="text-align:center;" | Eb
+|-
+| style="text-align:center;" | 4
+| style="text-align:center;" | 184.62
+| style="text-align:center;" | [[9/8|9/8]], [[10/9|10/9]], [[11/10|11/10]]
+| style="text-align:center;" | re
+| style="text-align:center;" | M2
+| style="text-align:center;" | E
+|-
+| style="text-align:center;" | 5
+| style="text-align:center;" | 230.77
+| style="text-align:center;" | [[8/7|8/7]], 15/13
+| style="text-align:center;" | ri
+| style="text-align:center;" | A2
+| style="text-align:center;" | E#
+|-
+| style="text-align:center;" | 6
+| style="text-align:center;" | 276.92
+| style="text-align:center;" | [[7/6|7/6]], [[13/11|13/11]], [[33/28|33/28]]
+| style="text-align:center;" | ma
+| style="text-align:center;" | d3
+| style="text-align:center;" | Fb
+|-
+| style="text-align:center;" | 7
+| style="text-align:center;" | 323.08
+| style="text-align:center;" | [[6/5|6/5]]
+| style="text-align:center;" | me
+| style="text-align:center;" | m3
+| style="text-align:center;" | F
+|-
+| style="text-align:center;" | 8
+| style="text-align:center;" | 369.23
+| style="text-align:center;" | [[5/4|5/4]], [[11/9|11/9]], [[16/13|16/13]]
+| style="text-align:center;" | muh/mi
+| style="text-align:center;" | M3
+| style="text-align:center;" | F#
+|-
+| style="text-align:center;" | 9
+| style="text-align:center;" | 415.38
+| style="text-align:center;" | [[9/7|9/7]], [[14/11|14/11]], [[33/26|33/26]]
+| style="text-align:center;" | maa
+| style="text-align:center;" | A3
+| style="text-align:center;" | Fx
+|-
+| style="text-align:center;" | 10
+| style="text-align:center;" | 461.54
+| style="text-align:center;" | [[21/16|21/16]], [[13/10|13/10]]
+| style="text-align:center;" | fe
+| style="text-align:center;" | d4
+| style="text-align:center;" | Gb
+|-
+| style="text-align:center;" | 11
+| style="text-align:center;" | 507.69
+| style="text-align:center;" | [[4/3|4/3]]
+| style="text-align:center;" | fa
+| style="text-align:center;" | P4
+| style="text-align:center;" | G
+|-
+| style="text-align:center;" | 12
+| style="text-align:center;" | 553.85
+| style="text-align:center;" | [[11/8|11/8]], [[18/13|18/13]]
+| style="text-align:center;" | fu
+| style="text-align:center;" | A4
+| style="text-align:center;" | G#
+|-
+| style="text-align:center;" | 13
+| style="text-align:center;" | 600<span style="color: #ffffff;">.00</span>
+| style="text-align:center;" | [[7/5|7/5]], [[10/7|10/7]]
+| style="text-align:center;" | fi/se
+| style="text-align:center;" | AA4, dd5
+| style="text-align:center;" | Gx, Abb
+|-
+| style="text-align:center;" | 14
+| style="text-align:center;" | 646.15
+| style="text-align:center;" | [[16/11|16/11]], [[13/9|13/9]]
+| style="text-align:center;" | su
+| style="text-align:center;" | d5
+| style="text-align:center;" | Ab
+|-
+| style="text-align:center;" | 15
+| style="text-align:center;" | 692.31
+| style="text-align:center;" | [[3/2|3/2]]
+| style="text-align:center;" | sol
+| style="text-align:center;" | P5
+| style="text-align:center;" | A
+|-
+| style="text-align:center;" | 16
+| style="text-align:center;" | 738.46
+| style="text-align:center;" | [[32/21|32/21]], [[20/13|20/13]]
+| style="text-align:center;" | si
+| style="text-align:center;" | A5
+| style="text-align:center;" | A#
+|-
+| style="text-align:center;" | 17
+| style="text-align:center;" | 784.62
+| style="text-align:center;" | [[11/7|11/7]], [[14/9|14/9]]
+| style="text-align:center;" | leh
+| style="text-align:center;" | d6
+| style="text-align:center;" | Bbb
+|-
+| style="text-align:center;" | 18
+| style="text-align:center;" | 830.77
+| style="text-align:center;" | [[13/8|13/8]], [[8/5|8/5]]
+| style="text-align:center;" | le/lu
+| style="text-align:center;" | m6
+| style="text-align:center;" | Bb
+|-
+| style="text-align:center;" | 19
+| style="text-align:center;" | 876.92
+| style="text-align:center;" | [[5/3|5/3]]
+| style="text-align:center;" | la
+| style="text-align:center;" | M6
+| style="text-align:center;" | B
+|-
+| style="text-align:center;" | 20
+| style="text-align:center;" | 923.08
+| style="text-align:center;" | [[12/7|12/7]], [[22/13|22/13]]
+| style="text-align:center;" | li
+| style="text-align:center;" | A6
+| style="text-align:center;" | B#
+|-
+| style="text-align:center;" | 21
+| style="text-align:center;" | 969.23
+| style="text-align:center;" | [[7/4|7/4]]
+| style="text-align:center;" | ta
+| style="text-align:center;" | d7
+| style="text-align:center;" | Cb
+|-
+| style="text-align:center;" | 22
+| style="text-align:center;" | 1015.38
+| style="text-align:center;" | [[9/5|9/5]], [[16/9|16/9]], [[20/11|20/11]]
+| style="text-align:center;" | te
+| style="text-align:center;" | m7
+| style="text-align:center;" | C
+|-
+| style="text-align:center;" | 23
+| style="text-align:center;" | 1061.54
+| style="text-align:center;" | [[11/6|11/6]], [[13/7|13/7]], [[15/8|15/8]], [[24/13|24/13]]
+| style="text-align:center;" | tu/ti
+| style="text-align:center;" | M7
+| style="text-align:center;" | C#
+|-
+| style="text-align:center;" | 24
+| style="text-align:center;" | 1107.69
+| style="text-align:center;" | [[21/11|21/11]], [[25/13|25/13]], [[40/21|40/21]]
+| style="text-align:center;" | to
+| style="text-align:center;" | A7
+| style="text-align:center;" | Cx
+|-
+| style="text-align:center;" | 25
+| style="text-align:center;" | 1153.85
+| style="text-align:center;" | [[64/33|64/33]], [[96/49|96/49]], [[35/18|35/18]], [[48/25|48/25]]
+| style="text-align:center;" | da
+| style="text-align:center;" | d8
+| style="text-align:center;" | Db
+|-
+| style="text-align:center;" | 26
+| style="text-align:center;" | 1200<span style="color: #ffffff;">.00</span>
+| style="text-align:center;" | 2/1
+| style="text-align:center;" | do
+| style="text-align:center;" | P8
+| style="text-align:center;" | D
+|}
 *based on treating 26-EDO as a 13-limit temperament; other approaches are possible.
-Using [[Kite's color notation|color notation]], qualities can be loosely associated with colors:
+Using [[Kite's_color_notation|color notation]], qualities can be loosely associated with colors:
-||~ quality ||~ color ||~ monzo format ||~ examples ||
-||= diminished ||= blue ||= {a, b, 0, 1} ||= 7/6, 7/4 ||
+{| class="wikitable"
-||= minor ||= fourthward white ||= {a, b}, b &lt; -1 ||= 32/27, 16/9 ||
+|-
-||= " ||= green ||= {a, b, -1} ||= 6/5, 9/5 ||
+! | quality
-||= major ||= yellow ||= {a, b, 1} ||= 5/4, 5/3 ||
+! | color
-||= " ||= fifthward white ||= {a, b}, b &gt; 1 ||= 9/8, 27/16 ||
+! | monzo format
-||= augmented ||= red ||= {a, b, 0, -1} ||= 9/7, 12/7 ||
+! | examples
+|-
+| style="text-align:center;" | diminished
+| style="text-align:center;" | blue
+| style="text-align:center;" | {a, b, 0, 1}
+| style="text-align:center;" | 7/6, 7/4
+|-
+| style="text-align:center;" | minor
+| style="text-align:center;" | fourthward white
+| style="text-align:center;" | {a, b}, b &lt; -1
+| style="text-align:center;" | 32/27, 16/9
+|-
+| style="text-align:center;" | "
+| style="text-align:center;" | green
+| style="text-align:center;" | {a, b, -1}
+| style="text-align:center;" | 6/5, 9/5
+|-
+| style="text-align:center;" | major
+| style="text-align:center;" | yellow
+| style="text-align:center;" | {a, b, 1}
+| style="text-align:center;" | 5/4, 5/3
+|-
+| style="text-align:center;" | "
+| style="text-align:center;" | fifthward white
+| style="text-align:center;" | {a, b}, b &gt; 1
+| style="text-align:center;" | 9/8, 27/16
+|-
+| style="text-align:center;" | augmented
+| style="text-align:center;" | red
+| style="text-align:center;" | {a, b, 0, -1}
+| style="text-align:center;" | 9/7, 12/7
+|}
 All 26edo chords can be named using conventional methods, expanded to include augmented and diminished 2nd, 3rds, 6ths and 7ths. Spelling certain chords properly may require triple sharps and flats, especially if the tonic is anything other than the 11 keys in the Eb-C# range. Here are the blue, green, yellow and red triads
-||~ color of the 3rd ||~ JI chord ||~ notes as edosteps ||~ notes of C chord ||~ written name ||~ spoken name ||
-||= blue ||= 6:7:9 ||= 0-6-15 ||= C Ebb G ||= C(b3) or C(d3) ||= C flat-three or C dim-three ||
-||= green ||= 10:12:15 ||= 0-7-15 ||= C Eb G ||= Cm ||= C minor ||
-||= yellow ||= 4:5:6 ||= 0-8-15 ||= C E G ||= C ||= C major or C ||
-||= red ||= 14:18:27 ||= 0-9-15 ||= C E# G ||= C(#3) or C(A3) ||= C sharp-three or C aug-three ||
-For a more complete list, see [[xenharmonic/Ups and Downs Notation#Chord%20names%20in%20other%20EDOs|Ups and Downs Notation - Chord names in other EDOs]].
-==Selected just intervals by error==
+{| class="wikitable"
+|-
+! | color of the 3rd
+! | JI chord
+! | notes as edosteps
+! | notes of C chord
+! | written name
+! | spoken name
+|-
+| style="text-align:center;" | blue
+| style="text-align:center;" | 6:7:9
+| style="text-align:center;" | 0-6-15
+| style="text-align:center;" | C Ebb G
+| style="text-align:center;" | C(b3) or C(d3)
+| style="text-align:center;" | C flat-three or C dim-three
+|-
+| style="text-align:center;" | green
+| style="text-align:center;" | 10:12:15
+| style="text-align:center;" | 0-7-15
+| style="text-align:center;" | C Eb G
+| style="text-align:center;" | Cm
+| style="text-align:center;" | C minor
+|-
+| style="text-align:center;" | yellow
+| style="text-align:center;" | 4:5:6
+| style="text-align:center;" | 0-8-15
+| style="text-align:center;" | C E G
+| style="text-align:center;" | C
+| style="text-align:center;" | C major or C
+|-
+| style="text-align:center;" | red
+| style="text-align:center;" | 14:18:27
+| style="text-align:center;" | 0-9-15
+| style="text-align:center;" | C E# G
+| style="text-align:center;" | C(#3) or C(A3)
+| style="text-align:center;" | C sharp-three or C aug-three
+|}
+For a more complete list, see [[Ups_and_Downs_Notation#Chord names in other EDOs|Ups and Downs Notation - Chord names in other EDOs]].
+==Selected just intervals by error==
 The following table shows how [[Just-24|some prominent just intervals]] are represented in 26edo (ordered by absolute error).
-||~ Interval, complement ||~ Error (abs., in [[cent|cents]]) ||
-||= [[13_12|13/12]], [[24_13|24/13]] ||= 0.111 ||
-||= [[8_7|8/7]], [[7_4|7/4]] ||= 0.405 ||
-||= [[14_11|14/11]], [[11_7|11/7]] ||= 2.123 ||
-||= [[10_9|10/9]], [[9_5|9/5]] ||= 2.212 ||
-||= [[11_8|11/8]], [[16_11|16/11]] ||= 2.528 ||
-||= [[13_10|13/10]], [[20_13|20/13]] ||= 7.325 ||
-||= [[6_5|6/5]], [[5_3|5/3]] ||= 7.436 ||
-||= [[18_13|18/13]], [[13_9|13/9]] ||= 9.536 ||
-||= [[4_3|4/3]], [[3_2|3/2]] ||= 9.647 ||
-||= [[16_13|16/13]], [[13_8|13/8]] ||= 9.758 ||
-||= [[7_6|7/6]], [[12_7|12/7]] ||= 10.052 ||
-||= [[14_13|14/13]], [[13_7|13/7]] ||= 10.163 ||
-||= [[12_11|12/11]], [[11_6|11/6]] ||= 12.176 ||
-||= [[13_11|13/11]], [[22_13|22/13]] ||= 12.287 ||
-||= [[15_11|15/11]], [[22_15|22/15]] ||= 16.895 ||
-||= [[15_13|15/13]], [[26_15|26/15]] ||= 16.972 ||
-||= [[5_4|5/4]], [[8_5|8/5]] ||= 17.083 ||
-||= [[7_5|7/5]], [[10_7|10/7]] ||= 17.488 ||
-||= [[15_14|15/14]], [[28_15|28/15]] ||= 19.019 ||
-||= [[9_8|9/8]], [[16_9|16/9]] ||= 19.295 ||
-||= [[16_15|16/15]], [[15_8|15/8]] ||= 19.424 ||
-||= [[11_10|11/10]], [[20_11|20/11]] ||= 19.611 ||
-||= [[9_7|9/7]], [[14_9|14/9]] ||= 19.699 ||
-||= [[11_9|11/9]], [[18_11|18/11]] ||= 21.823 ||
-=Rank two temperaments=
+{| class="wikitable"
-[[List of 26et rank two temperaments by badness]]
+|-
-[[List of edo-distinct 26et rank two temperaments]]
+! | Interval, complement
-||~ Periods
+! | Error (abs., in [[cent|cents]])
-per octave ||~ Generator ||~ Temperaments ||
+|-
-||= 1 ||= 1\26 || [[Quartonic]]/Quarto ||
+| style="text-align:center;" | [[13/12|13/12]], [[24/13|24/13]]
-||= 1 ||= 3\26 || [[Jerome]]/[[Chromatic pairs|Bleu]]/Secund ||
+| style="text-align:center;" | 0.111
-||= 1 ||= 5\26 || [[Cynder]]/[[Mothra]] ||
+|-
-||= 1 ||= 7\26 || [[Superkleismic]]/[[Orgone]]/[[Shibboleth]] ||
+| style="text-align:center;" | [[8/7|8/7]], [[7/4|7/4]]
-||= 1 ||= 9\26 || [[Roman]]/Wesley ||
+| style="text-align:center;" | 0.405
-||= 1 ||= 11\26 || [[Meantone]]/[[Flattone]] ||
+|-
-||= 2 ||= 1\26 || Elvis ||
+| style="text-align:center;" | [[14/11|14/11]], [[11/7|11/7]]
-||= 2 ||= 2\26 || [[Injera]] ||
+| style="text-align:center;" | 2.123
-||= 2 ||= 3\26 || [[Fifive]]/Crepuscular ||
+|-
-||= 2 ||= 4\26 || [[Unidec]]/[[Gamelismic clan#Unidec-Hendec|Hendec]]/Dubbla ||
+| style="text-align:center;" | [[10/9|10/9]], [[9/5|9/5]]
-||= 2 ||= 5\26 || [[Lemba]] ||
+| style="text-align:center;" | 2.212
-||= 2 ||= 6\26 || [[Doublewide]]/Cavalier ||
+|-
-||= 13 ||= 1\26 || Triskaidekic ||
+| style="text-align:center;" | [[11/8|11/8]], [[16/11|16/11]]
+| style="text-align:center;" | 2.528
+|-
+| style="text-align:center;" | [[13/10|13/10]], [[20/13|20/13]]
+| style="text-align:center;" | 7.325
+|-
+| style="text-align:center;" | [[6/5|6/5]], [[5/3|5/3]]
+| style="text-align:center;" | 7.436
+|-
+| style="text-align:center;" | [[18/13|18/13]], [[13/9|13/9]]
+| style="text-align:center;" | 9.536
+|-
+| style="text-align:center;" | [[4/3|4/3]], [[3/2|3/2]]
+| style="text-align:center;" | 9.647
+|-
+| style="text-align:center;" | [[16/13|16/13]], [[13/8|13/8]]
+| style="text-align:center;" | 9.758
+|-
+| style="text-align:center;" | [[7/6|7/6]], [[12/7|12/7]]
+| style="text-align:center;" | 10.052
+|-
+| style="text-align:center;" | [[14/13|14/13]], [[13/7|13/7]]
+| style="text-align:center;" | 10.163
+|-
+| style="text-align:center;" | [[12/11|12/11]], [[11/6|11/6]]
+| style="text-align:center;" | 12.176
+|-
+| style="text-align:center;" | [[13/11|13/11]], [[22/13|22/13]]
+| style="text-align:center;" | 12.287
+|-
+| style="text-align:center;" | [[15/11|15/11]], [[22/15|22/15]]
+| style="text-align:center;" | 16.895
+|-
+| style="text-align:center;" | [[15/13|15/13]], [[26/15|26/15]]
+| style="text-align:center;" | 16.972
+|-
+| style="text-align:center;" | [[5/4|5/4]], [[8/5|8/5]]
+| style="text-align:center;" | 17.083
+|-
+| style="text-align:center;" | [[7/5|7/5]], [[10/7|10/7]]
+| style="text-align:center;" | 17.488
+|-
+| style="text-align:center;" | [[15/14|15/14]], [[28/15|28/15]]
+| style="text-align:center;" | 19.019
+|-
+| style="text-align:center;" | [[9/8|9/8]], [[16/9|16/9]]
+| style="text-align:center;" | 19.295
+|-
+| style="text-align:center;" | [[16/15|16/15]], [[15/8|15/8]]
+| style="text-align:center;" | 19.424
+|-
+| style="text-align:center;" | [[11/10|11/10]], [[20/11|20/11]]
+| style="text-align:center;" | 19.611
+|-
+| style="text-align:center;" | [[9/7|9/7]], [[14/9|14/9]]
+| style="text-align:center;" | 19.699
+|-
+| style="text-align:center;" | [[11/9|11/9]], [[18/11|18/11]]
+| style="text-align:center;" | 21.823
+|}
+=Rank two temperaments=
+[[List_of_26et_rank_two_temperaments_by_badness|List of 26et rank two temperaments by badness]]
-==Hendec in 26et==
+[[List_of_edo-distinct_26et_rank_two_temperaments|List of edo-distinct 26et rank two temperaments]]
-[[Gamelismic clan#Unidec-Hendec|Hendec]], the 13-limit 26&amp;46 temperament with generator ~10/9, concentrates the intervals of greatest accuracy in 26et into the lower ranges of complexity. It has a period of half an octave, with 13/12 reachable by four generators, 8/7 by two, 14/11 by one, 10/9 by one, and 11/8 by three. All of these are tuned to within 2.5 cents of accuracy.
-=Commas=
+{| class="wikitable"
-et tempers out the following commas. (Note: This assumes the val &lt; 26 41 60 73 90 96 |.)
+|-
-||~ Ratio ||~ Monzo ||~ Size (Cents) ||~ Name 1 ||~ Name 2 ||~ Name 3 ||
+! | Periods
-||= 81/80 ||&lt; | -4 4 -1 &gt; ||&gt; 21.51 ||= Syntonic Comma ||= Didymos Comma ||= Meantone Comma ||
-||= 5696703/5695946 ||&lt; | -17 62 -35 &gt; ||&gt; 0.23 ||= Senior ||=   ||=   ||
-||= 525/512 ||&lt; | -9 1 2 1 &gt; ||&gt; 43.41 ||= Avicennma ||= Avicenna's Enharmonic Diesis ||=   ||
-||= 50/49 ||&lt; | 1 0 2 -2 &gt; ||&gt; 34.98 ||= Tritonic Diesis ||= Jubilisma ||=   ||
-||= 875/864 ||&lt; | -5 -3 3 1 &gt; ||&gt; 21.90 ||= Keema ||=   ||=   ||
-||= 4000/3969 ||&lt; | 5 -4 3 -2 &gt; ||&gt; 13.47 ||= Octagar ||=   ||=   ||
-||= 1728/1715 ||&lt; | 6 3 -1 -3 &gt; ||&gt; 13.07 ||= Orwellisma ||= Orwell Comma ||=   ||
-||= 1029/1024 ||&lt; | -10 1 0 3 &gt; ||&gt; 8.43 ||= Gamelisma ||=   ||=   ||
-||= 321489/320000 ||&lt; | -9 8 -4 2 &gt; ||&gt; 8.04 ||= Varunisma ||=   ||=   ||
-||= 1065875/1063543 ||&lt; | -26 -1 1 9 &gt; ||&gt; 3.79 ||= Wadisma ||=   ||=   ||
-||= 4375/4374 ||&lt; | -1 -7 4 1 &gt; ||&gt; 0.40 ||= Ragisma ||=   ||=   ||
-||= 99/98 ||&lt; | -1 2 0 -2 1 &gt; ||&gt; 17.58 ||= Mothwellsma ||=   ||=   ||
-||= 100/99 ||&lt; | 2 -2 2 0 -1 &gt; ||&gt; 17.40 ||= Ptolemisma ||=   ||=   ||
-||= 105/104 ||&lt; | -3 1 1 1 0 -1 &gt; ||&gt; 16.57 ||= Animist ||=   ||=   ||
-||= 65536/65219 ||&lt; | 16 0 0 -2 -3 &gt; ||&gt; 8.39 ||= Orgonisma ||=   ||=   ||
-||= 385/384 ||&lt; | -7 -1 1 1 1 &gt; ||&gt; 4.50 ||= Keenanisma ||=   ||=   ||
-||= 441/440 ||&lt; | -3 2 -1 2 -1 &gt; ||&gt; 3.93 ||= Werckisma ||=   ||=   ||
-||= 3025/3024 ||&lt; | -4 -3 2 -1 2 &gt; ||&gt; 0.57 ||= Lehmerisma ||=   ||=   ||
-||= 9801/9800 ||&lt; | -3 4 -2 -2 2 &gt; ||&gt; 0.18 ||= Kalisma ||= Gauss' Comma ||=   ||
-=[[Orgonia|Orgone Temperament]]=
-[[Andrew Heathwaite]] first proposed orgone temperament to take advantage of 26edo's excellent 11 and 7 approximations. 7 degrees of 26edo is a wide minor third of approximately 323.077 cents, and that interval taken as a generator produces 7-tone and 11-tone MOS scales:
+per octave
+! | Generator
+! | Temperaments
+|-
+| style="text-align:center;" | 1
+| style="text-align:center;" | 1\26
+| | [[Quartonic|Quartonic]]/Quarto
+|-
+| style="text-align:center;" | 1
+| style="text-align:center;" | 3\26
+| | [[Jerome|Jerome]]/[[Chromatic_pairs|Bleu]]/Secund
+|-
+| style="text-align:center;" | 1
+| style="text-align:center;" | 5\26
+| | [[Cynder|Cynder]]/[[Mothra|Mothra]]
+|-
+| style="text-align:center;" | 1
+| style="text-align:center;" | 7\26
+| | [[Superkleismic|Superkleismic]]/[[Orgone|Orgone]]/[[Shibboleth|Shibboleth]]
+|-
+| style="text-align:center;" | 1
+| style="text-align:center;" | 9\26
+| | [[Roman|Roman]]/Wesley
+|-
+| style="text-align:center;" | 1
+| style="text-align:center;" | 11\26
+| | [[Meantone|Meantone]]/[[Flattone|Flattone]]
+|-
+| style="text-align:center;" | 2
+| style="text-align:center;" | 1\26
+| | Elvis
+|-
+| style="text-align:center;" | 2
+| style="text-align:center;" | 2\26
+| | [[Injera|Injera]]
+|-
+| style="text-align:center;" | 2
+| style="text-align:center;" | 3\26
+| | [[Fifive|Fifive]]/Crepuscular
+|-
+| style="text-align:center;" | 2
+| style="text-align:center;" | 4\26
+| | [[Unidec|Unidec]]/[[Gamelismic_clan#Unidec-Hendec|Hendec]]/Dubbla
+|-
+| style="text-align:center;" | 2
+| style="text-align:center;" | 5\26
+| | [[Lemba|Lemba]]
+|-
+| style="text-align:center;" | 2
+| style="text-align:center;" | 6\26
+| | [[Doublewide|Doublewide]]/Cavalier
+|-
+| style="text-align:center;" | 13
+| style="text-align:center;" | 1\26
+| | Triskaidekic
+|}
-The 7-tone scale in degrees-in-between: 5 2 5 2 5 2 5. [[MOSScales|MOS]] of type [[4L 3s|4L 3s (mish)]].
+==Hendec in 26et==
-The 7-tone scale in cents: 0 231 323 554 646 877 969 1200.
+[[Gamelismic_clan#Unidec-Hendec|Hendec]], the 13-limit 26&amp;46 temperament with generator ~10/9, concentrates the intervals of greatest accuracy in 26et into the lower ranges of complexity. It has a period of half an octave, with 13/12 reachable by four generators, 8/7 by two, 14/11 by one, 10/9 by one, and 11/8 by three. All of these are tuned to within 2.5 cents of accuracy.
-The 11-tone scale in degrees-in-between: 2 3 2 2 3 2 3 2 2 3 2. [[MOSScales|MOS]] of type [[4L 7s]].
+=Commas=
-The 11-tone scale in cents: 0 92 231 323 415 554 646 785 877 969 1108 1200.
+et tempers out the following commas. (Note: This assumes the val &lt; 26 41 60 73 90 96 |.)
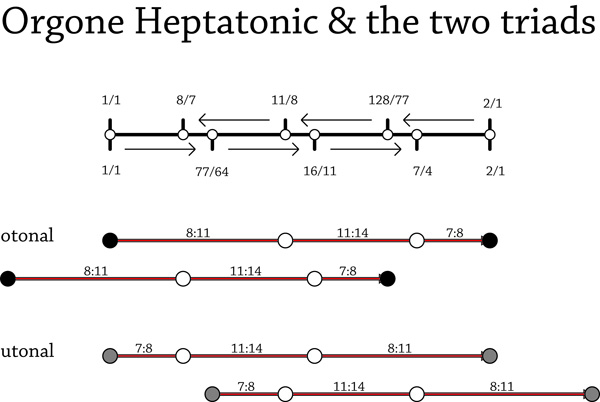
-The primary triad for orgone temperament is 8:11:14 and its subharmonic inversion, which these scales have in abundance. 2g approximates [[16_11|16:11]] and 3g approximates [[7_4|7:4]] (and I would call that the definition of Orgone Temperament). That also implies that g approximates the difference between 7:4 and 16:11, which is 77:64, about 320.1 cents.
+{| class="wikitable"
+|-
+! | Ratio
+! | Monzo
+! | Size (Cents)
+! | Name 1
+! | Name 2
+! | Name 3
+|-
+| style="text-align:center;" | 81/80
+| | | -4 4 -1 &gt;
+| style="text-align:right;" | 21.51
+| style="text-align:center;" | Syntonic Comma
+| style="text-align:center;" | Didymos Comma
+| style="text-align:center;" | Meantone Comma
+|-
+| style="text-align:center;" | 5696703/5695946
+| | | -17 62 -35 &gt;
+| style="text-align:right;" | 0.23
+| style="text-align:center;" | Senior
+| style="text-align:center;" |
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 525/512
+| | | -9 1 2 1 &gt;
+| style="text-align:right;" | 43.41
+| style="text-align:center;" | Avicennma
+| style="text-align:center;" | Avicenna's Enharmonic Diesis
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 50/49
+| | | 1 0 2 -2 &gt;
+| style="text-align:right;" | 34.98
+| style="text-align:center;" | Tritonic Diesis
+| style="text-align:center;" | Jubilisma
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 875/864
+| | | -5 -3 3 1 &gt;
+| style="text-align:right;" | 21.90
+| style="text-align:center;" | Keema
+| style="text-align:center;" |
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 4000/3969
+| | | 5 -4 3 -2 &gt;
+| style="text-align:right;" | 13.47
+| style="text-align:center;" | Octagar
+| style="text-align:center;" |
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 1728/1715
+| | | 6 3 -1 -3 &gt;
+| style="text-align:right;" | 13.07
+| style="text-align:center;" | Orwellisma
+| style="text-align:center;" | Orwell Comma
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 1029/1024
+| | | -10 1 0 3 &gt;
+| style="text-align:right;" | 8.43
+| style="text-align:center;" | Gamelisma
+| style="text-align:center;" |
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 321489/320000
+| | | -9 8 -4 2 &gt;
+| style="text-align:right;" | 8.04
+| style="text-align:center;" | Varunisma
+| style="text-align:center;" |
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 1065875/1063543
+| | | -26 -1 1 9 &gt;
+| style="text-align:right;" | 3.79
+| style="text-align:center;" | Wadisma
+| style="text-align:center;" |
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 4375/4374
+| | | -1 -7 4 1 &gt;
+| style="text-align:right;" | 0.40
+| style="text-align:center;" | Ragisma
+| style="text-align:center;" |
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 99/98
+| | | -1 2 0 -2 1 &gt;
+| style="text-align:right;" | 17.58
+| style="text-align:center;" | Mothwellsma
+| style="text-align:center;" |
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 100/99
+| | | 2 -2 2 0 -1 &gt;
+| style="text-align:right;" | 17.40
+| style="text-align:center;" | Ptolemisma
+| style="text-align:center;" |
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 105/104
+| | | -3 1 1 1 0 -1 &gt;
+| style="text-align:right;" | 16.57
+| style="text-align:center;" | Animist
+| style="text-align:center;" |
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 65536/65219
+| | | 16 0 0 -2 -3 &gt;
+| style="text-align:right;" | 8.39
+| style="text-align:center;" | Orgonisma
+| style="text-align:center;" |
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 385/384
+| | | -7 -1 1 1 1 &gt;
+| style="text-align:right;" | 4.50
+| style="text-align:center;" | Keenanisma
+| style="text-align:center;" |
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 441/440
+| | | -3 2 -1 2 -1 &gt;
+| style="text-align:right;" | 3.93
+| style="text-align:center;" | Werckisma
+| style="text-align:center;" |
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 3025/3024
+| | | -4 -3 2 -1 2 &gt;
+| style="text-align:right;" | 0.57
+| style="text-align:center;" | Lehmerisma
+| style="text-align:center;" |
+| style="text-align:center;" |
+|-
+| style="text-align:center;" | 9801/9800
+| | | -3 4 -2 -2 2 &gt;
+| style="text-align:right;" | 0.18
+| style="text-align:center;" | Kalisma
+| style="text-align:center;" | Gauss' Comma
+| style="text-align:center;" |
+|}
-[[37edo]] is another orgone tuning, and [[89edo]] is better even than 26. If we take 11 and 26 to be the edges of the Orgone Spectrum, we may fill in the rest of the spectrum thus:
+=[[Orgonia|Orgone Temperament]]=
-|| 3\11 ||   ||   ||   ||   ||
+[[Andrew_Heathwaite|Andrew Heathwaite]] first proposed orgone temperament to take advantage of 26edo's excellent 11 and 7 approximations. 7 degrees of 26edo is a wide minor third of approximately 323.077 cents, and that interval taken as a generator produces 7-tone and 11-tone MOS scales:
-||   ||   ||   ||   || 19\70 ||
-||   ||   ||   || 16\59 ||   ||
-||   ||   ||   ||   || 29\107 ||
-||   ||   || 13\48 ||   ||   ||
-||   ||   ||   ||   || 36\133 ||
-||   ||   ||   || 23\85 ||   ||
-||   ||   ||   ||   || 33\122 ||
-||   || 10\37 ||   ||   ||   ||
-||   ||   ||   ||   || 37\137 ||
-||   ||   ||   || 27\100 ||   ||
-||   ||   ||   ||   || 44\163 ||
-||   ||   || 17\63 ||   ||   ||
-||   ||   ||   ||   || 41\152 ||
-||   ||   ||   || 24\89 ||   ||
-||   ||   ||   ||   || 31\115 ||
-|| 7\26 ||   ||   ||   ||   ||
-Orgone has a minimax tuning which sharpens both 7 and 11 by 1/5 of an orgonisma, or 1.679 cents. This makes the generator g a 77/64 sharp by 2/5 of the orgonisma. From this we may conclude that 24/89 or 31/115 would be reasonable alternatives to the 7/26 generator.
+The 7-tone scale in degrees-in-between: 5 2 5 2 5 2 5. [[MOSScales|MOS]] of type [[4L_3s|4L 3s (mish)]].
-[[image:orgone_heptatonic.jpg]]
+The 7-tone scale in cents: 0 231 323 554 646 877 969 1200.
+The 11-tone scale in degrees-in-between: 2 3 2 2 3 2 3 2 2 3 2. [[MOSScales|MOS]] of type [[4L_7s|4L 7s]].
-=Additional Scalar Bases Available in 26-EDO:=
+The 11-tone scale in cents: 0 92 231 323 415 554 646 785 877 969 1108 1200.
-Since the perfect 5th in 26-EDO spans 15 degrees, it can be divided into three equal parts (each approximately an 8/7) as well as five equal parts (each approximately a 13/12). The former approach produces MOS at 1L+4s, 5L+1s, and 5L+6s (5 5 5 5 6, 5 5 5 5 5 1, and 4 1 4 1 4 1 4 1 4 1 1 respectively), and is excellent for 4:6:7 triads. The latter produces MOS at 1L+7s and 8L+1s (3 3 3 3 3 3 3 5 and 3 3 3 3 3 3 3 3 2 respectively), and is fairly well-supplied with 4:6:7:11:13 pentads. It also works well for more conventional (though further from Just) 6:7:9 triads, as well as 4:5:6 triads that use the worse mapping for 5 (making 5/4 the 415.38-cent interval).
--Igs
+The primary triad for orgone temperament is 8:11:14 and its subharmonic inversion, which these scales have in abundance. 2g approximates [[16/11|16:11]] and 3g approximates [[7/4|7:4]] (and I would call that the definition of Orgone Temperament). That also implies that g approximates the difference between 7:4 and 16:11, which is 77:64, about 320.1 cents.
-=Literature=
+[[37edo|37edo]] is another orgone tuning, and [[89edo|89edo]] is better even than 26. If we take 11 and 26 to be the edges of the Orgone Spectrum, we may fill in the rest of the spectrum thus:
-[[http://www.ronsword.com|Sword, Ron. **Icosihexaphonic Scales for Guitar**. IAAA Press. 2010 - A Guitar-scale thesaurus for 26-EDO.]]
+{| class="wikitable"
+|-
+| | 3\11
+| |
+| |
+| |
+| |
+|-
+| |
+| |
+| |
+| |
+| | 19\70
+|-
+| |
+| |
+| |
+| | 16\59
+| |
+|-
+| |
+| |
+| |
+| |
+| | 29\107
+|-
+| |
+| |
+| | 13\48
+| |
+| |
+|-
+| |
+| |
+| |
+| |
+| | 36\133
+|-
+| |
+| |
+| |
+| | 23\85
+| |
+|-
+| |
+| |
+| |
+| |
+| | 33\122
+|-
+| |
+| | 10\37
+| |
+| |
+| |
+|-
+| |
+| |
+| |
+| |
+| | 37\137
+|-
+| |
+| |
+| |
+| | 27\100
+| |
+|-
+| |
+| |
+| |
+| |
+| | 44\163
+|-
+| |
+| |
+| | 17\63
+| |
+| |
+|-
+| |
+| |
+| |
+| |
+| | 41\152
+|-
+| |
+| |
+| |
+| | 24\89
+| |
+|-
+| |
+| |
+| |
+| |
+| | 31\115
+|-
+| | 7\26
+| |
+| |
+| |
+| |
+|}
-=Compositions=
+Orgone has a minimax tuning which sharpens both 7 and 11 by 1/5 of an orgonisma, or 1.679 cents. This makes the generator g a 77/64 sharp by 2/5 of the orgonisma. From this we may conclude that 24/89 or 31/115 would be reasonable alternatives to the 7/26 generator.
-[[http://soonlabel.com/xenharmonic/archives/3335|Canon 3-in-1 on a ground ‘The tempest’, by Claudi Meneghin]]
+[[File:orgone_heptatonic.jpg|alt=orgone_heptatonic.jpg|orgone_heptatonic.jpg]]
-&lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;[[http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Igs/City%20Of%20The%20Asleep%20-%20A%20Time-Yellowed%20Photograph%20of%20Cliffs%20Hangs%20in%20the%20Hall.mp3|A Time-Yellowed Photo of the Cliffs Hangs on the Wall ]]&lt;/span&gt; by [[IgliashonJones|Igliashon Jones]]
-&lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;[[http://micro.soonlabel.com/gene_ward_smith/Others/Igs/Two%20Pairs%20of%20Socks.mp3|Two Pairs of Socks]]&lt;/span&gt; by [[IgliashonJones|Igliashon Jones]]
-[[http://www.io.com/%7Ehmiller/midi/26tet.mid|Etude in 26-tone equal temperament]] &lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;[[http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Herman/26tet.mp3|play]]&lt;/span&gt; by [[Herman Miller]]
-[[http://archive.org/details/UnderTheHeatdome|under the heatDome]] [[http://archive.org/download/UnderTheHeatdome/under_the_heatDome.mp3|play]] by [[Jon Lyle Smith]]
-[[http://danielthompson.blogspot.com/2007/04/new-version-of-organ-study-1.html|A New Recording of Organ Study #1]] &lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;[[http://www.microtonalmusic.net/audio/organstudyremix26edo.mp3|play]]&lt;/span&gt; by [[Daniel Thompson]]
-&lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;[[http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Bobro/LittleFugueIn26_CBobro.mp3|Little Fugue in 26]]&lt;/span&gt; by [[Cameron Bobro]]
-&lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;[[http://soonlabel.com/xenharmonic/wp-content/uploads/2011/11/26-tone-fugue.mp3|26 tone fugue (unfinished)]]&lt;/span&gt; by Peter Kosmorsky (based on the melody he was singing in the shower, in orgone, to the presumed confusion of those in earshot)
-&lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;[[http://www.96edo.com/music/micro900607.mp3|Microtonal music in 26-EDO]]&lt;/span&gt; by [[Shaahin Mohajeri]]
-[[media type="custom" key="11317210"]]&lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;[[http://micro.soonlabel.com/gene_ward_smith/Others/Curley/Zach%20Curley%20-%20Chiapas%20Palenque.mp3|Chiapas Palenque]]&lt;/span&gt; by [[Zach Curley]]
-&lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;[[http://micro.soonlabel.com/gene_ward_smith/Others/Curley/Zach%20Curley%20-%20Injera%20Jam.mp3|Injera Jam]]&lt;/span&gt; by [[Zach Curley]]
-[[http://micro.soonlabel.com/gene_ward_smith/Others/Curley/Zach%20Curley%20-%20Guitar%20Serenade%20in%20Q%20Major.mp3|Guitar Serenade in Q Major]] by [[Zach Curley]]
-[[http://midiguru.wordpress.com/2013/01/06/public-rituals/|Public Rituals « Jim Aikin's Oblong Blob]] “The Triumphal Procession of Nebuchadnezzar“
-[[http://www.unfretted.com/microtonal/melopoeia-project-26-edo-album-based-on-tolkeins-silmarillion-ainulindale/|Melopœia Project – 26 EDO album based on Tolkein’s Silmarillion – Ainulindalë – Unfretted]]
-[[http://micro.soonlabel.com/26edo/20161224_26edo_wing.mp3|Morpheous Wing in 26 edo]] by [[Chris Vaisvil]]</pre></div>
-<h4>Original HTML content:</h4>
-<div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;width:200%;white-space: pre-wrap ! important" class="old-revision-html">&lt;html&gt;&lt;head&gt;&lt;title&gt;26edo&lt;/title&gt;&lt;/head&gt;&lt;body&gt;&lt;!-- ws:start:WikiTextTocRule:21:&amp;lt;img id=&amp;quot;wikitext@@toc@@normal&amp;quot; class=&amp;quot;WikiMedia WikiMediaToc&amp;quot; title=&amp;quot;Table of Contents&amp;quot; src=&amp;quot;/site/embedthumbnail/toc/normal?w=225&amp;amp;h=100&amp;quot;/&amp;gt; --&gt;&lt;div id="toc"&gt;&lt;h1 class="nopad"&gt;Table of Contents&lt;/h1&gt;&lt;!-- ws:end:WikiTextTocRule:21 --&gt;&lt;!-- ws:start:WikiTextTocRule:22: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#x-Structure"&gt;Structure&lt;/a&gt;&lt;/div&gt;
-&lt;!-- ws:end:WikiTextTocRule:22 --&gt;&lt;!-- ws:start:WikiTextTocRule:23: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#x-Intervals"&gt;Intervals&lt;/a&gt;&lt;/div&gt;
-&lt;!-- ws:end:WikiTextTocRule:23 --&gt;&lt;!-- ws:start:WikiTextTocRule:24: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#x-Selected just intervals by error"&gt;Selected just intervals by error&lt;/a&gt;&lt;/div&gt;
-&lt;!-- ws:end:WikiTextTocRule:24 --&gt;&lt;!-- ws:start:WikiTextTocRule:25: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Rank two temperaments"&gt;Rank two temperaments&lt;/a&gt;&lt;/div&gt;
-&lt;!-- ws:end:WikiTextTocRule:25 --&gt;&lt;!-- ws:start:WikiTextTocRule:26: --&gt;&lt;div style="margin-left: 2em;"&gt;&lt;a href="#Rank two temperaments-Hendec in 26et"&gt;Hendec in 26et&lt;/a&gt;&lt;/div&gt;
-&lt;!-- ws:end:WikiTextTocRule:26 --&gt;&lt;!-- ws:start:WikiTextTocRule:27: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Commas"&gt;Commas&lt;/a&gt;&lt;/div&gt;
-&lt;!-- ws:end:WikiTextTocRule:27 --&gt;&lt;!-- ws:start:WikiTextTocRule:28: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Orgone Temperament"&gt;Orgone Temperament&lt;/a&gt;&lt;/div&gt;
-&lt;!-- ws:end:WikiTextTocRule:28 --&gt;&lt;!-- ws:start:WikiTextTocRule:29: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Additional Scalar Bases Available in 26-EDO:"&gt;Additional Scalar Bases Available in 26-EDO:&lt;/a&gt;&lt;/div&gt;
-&lt;!-- ws:end:WikiTextTocRule:29 --&gt;&lt;!-- ws:start:WikiTextTocRule:30: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Literature"&gt;Literature&lt;/a&gt;&lt;/div&gt;
-&lt;!-- ws:end:WikiTextTocRule:30 --&gt;&lt;!-- ws:start:WikiTextTocRule:31: --&gt;&lt;div style="margin-left: 1em;"&gt;&lt;a href="#Compositions"&gt;Compositions&lt;/a&gt;&lt;/div&gt;
-&lt;!-- ws:end:WikiTextTocRule:31 --&gt;&lt;!-- ws:start:WikiTextTocRule:32: --&gt;&lt;/div&gt;
-&lt;!-- ws:end:WikiTextTocRule:32 --&gt;&lt;em&gt;26edo&lt;/em&gt; divides the &lt;a class="wiki_link" href="/octave"&gt;octave&lt;/a&gt; into 26 equal parts of 46.154 &lt;a class="wiki_link" href="/cent"&gt;cent&lt;/a&gt;s each. It tempers out 81/80 in the &lt;a class="wiki_link" href="/5-limit"&gt;5-limit&lt;/a&gt;, making it a meantone tuning with a very flat fifth. In the &lt;a class="wiki_link" href="/7-limit"&gt;7-limit&lt;/a&gt;, it tempers out 50/49, 525/512 and 875/864, and supports &lt;a class="wiki_link" href="/Meantone%20family"&gt;injera&lt;/a&gt;, &lt;a class="wiki_link" href="/Meantone%20family"&gt;flattone&lt;/a&gt;, &lt;a class="wiki_link" href="/Jubilismic%20clan#Lemba"&gt;lemba&lt;/a&gt; and &lt;a class="wiki_link" href="/Jubilismic%20clan#Doublewide"&gt;doublewide&lt;/a&gt; temperaments. It really comes into its own as a higher-limit temperament, being the smallest equal division which represents the &lt;a class="wiki_link" href="/13-limit"&gt;13 odd limit&lt;/a&gt; &lt;a class="wiki_link" href="/consistent"&gt;consistently&lt;/a&gt;. 26edo has a very good approximation of the harmonic seventh (&lt;a class="wiki_link" href="/7_4"&gt;7/4&lt;/a&gt;).&lt;br /&gt;
-&lt;br /&gt;
-edo's &amp;quot;minor sixth&amp;quot; is very close to phi (i. e., the golden ratio).&lt;br /&gt;
-&lt;br /&gt;
-&lt;!-- ws:start:WikiTextHeadingRule:1:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc0"&gt;&lt;a name="x-Structure"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:1 --&gt;Structure&lt;/h2&gt;
- &lt;br /&gt;
-The structure of 26edo is an interesting beast, with various approaches relating it to various rank two temperaments.&lt;br /&gt;
-. In terms of more traditional chord types we have flattone, a variant of meantone with flat fifths, which yields interesting but to some unsatisfying results (due mainly to the dissonance of its thirds, and its major seconds of either approximately &lt;a class="wiki_link" href="/10_9"&gt;10/9&lt;/a&gt; or &lt;a class="wiki_link" href="/8_7"&gt;8/7&lt;/a&gt;, but NOT &lt;a class="wiki_link" href="/9_8"&gt;9/8&lt;/a&gt;).&lt;br /&gt;
-. As two chains of meantone fifths half an octave apart, it supports injera temperament. The generator for this is an interval which can be called either 21/20 or 15/14, and which represents two steps of 26, and hence one step of 13. Hence in 26edo (as opposed to, for instance, 38edo) it can be viewed as two parallel 13edo scales, and from that point of view we can consider it as supporting the 13b&amp;amp;26 temperament, allowing the two chains be shifted slightly and which can be used for more atonal melodies. In this way its internal dynamics resemble those of 14edo.&lt;br /&gt;
-. 26edo nearly perfectly approximates the 7th and 11th harmonics, and an entire system may be constructed analogous to that based on the 3rd and 5th harmonics. In terms of subgroups, this is the 2.7.11 subgroup, and on this 26 tempers out the pair of commas 65536/65219 and | -3 0 0 6 -4&amp;gt;. The 65536/65219 comma, the orgonisma, leads to &lt;a class="wiki_link" href="/Orgonia"&gt;orgone temperament&lt;/a&gt; with an approximate 77/64 generator of 7\26, with MOS scales of size 7, 11 and 15. The | -3 0 0 6 -4&amp;gt; comma leads to a half-octave period and an approximate 49/44 generator of 4\26, leading to MOS of size 8 and 14.&lt;br /&gt;
-. We can also treat 26-EDO as a full 13-limit temperament, since it is consistent on the 13-limit (unlike all lower EDOs).&lt;br /&gt;
-. It also has a pretty good 17th harmonic and tempers out the comma 459:448, thus three fifths gives a 17:14 and four gives a 21:17; &amp;quot;mushtone&amp;quot;. Mushtone is high in badness, but 26edo does it pretty well (and &lt;a class="wiki_link" href="/33edo"&gt;33edo&lt;/a&gt; even better). Because 26edo also tempers out 85:84, the septendecimal major and minor thirds are equivalent to their pental counterparts, making mushtone the same as flattone.&lt;br /&gt;
-&lt;br /&gt;
-&lt;!-- ws:start:WikiTextHeadingRule:3:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc1"&gt;&lt;a name="x-Intervals"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:3 --&gt;Intervals&lt;/h2&gt;
-&lt;table class="wiki_table"&gt;
+=Additional Scalar Bases Available in 26-EDO:=
-    &lt;tr&gt;
+Since the perfect 5th in 26-EDO spans 15 degrees, it can be divided into three equal parts (each approximately an 8/7) as well as five equal parts (each approximately a 13/12). The former approach produces MOS at 1L+4s, 5L+1s, and 5L+6s (5 5 5 5 6, 5 5 5 5 5 1, and 4 1 4 1 4 1 4 1 4 1 1 respectively), and is excellent for 4:6:7 triads. The latter produces MOS at 1L+7s and 8L+1s (3 3 3 3 3 3 3 5 and 3 3 3 3 3 3 3 3 2 respectively), and is fairly well-supplied with 4:6:7:11:13 pentads. It also works well for more conventional (though further from Just) 6:7:9 triads, as well as 4:5:6 triads that use the worse mapping for 5 (making 5/4 the 415.38-cent interval).
-        &lt;th&gt;Degrees&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;Size in&lt;br /&gt;
-&lt;a class="wiki_link" href="/cent"&gt;cents&lt;/a&gt;&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;Approximate Ratios*&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;Solfege&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;Interval&lt;br /&gt;
-Name&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;Example&lt;br /&gt;
-in D&lt;br /&gt;
-&lt;/th&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;0&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;0&lt;span style="color: #ffffff;"&gt;.00&lt;/span&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;1/1&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;do&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;P1&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;D&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;1&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;46.15&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/33_32"&gt;33/32&lt;/a&gt;, &lt;a class="wiki_link" href="/49_48"&gt;49/48&lt;/a&gt;, &lt;a class="wiki_link" href="/36_35"&gt;36/35&lt;/a&gt;, &lt;a class="wiki_link" href="/25_24"&gt;25/24&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;di&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;A1&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;D#&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;2&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;92.31&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/21_20"&gt;21/20&lt;/a&gt;, &lt;a class="wiki_link" href="/22_21"&gt;22/21&lt;/a&gt;, &lt;a class="wiki_link" href="/26_25"&gt;26/25&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;rih&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;d2&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Ebb&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;3&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;138.46&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/12_11"&gt;12/11&lt;/a&gt;, &lt;a class="wiki_link" href="/13_12"&gt;13/12&lt;/a&gt;, &lt;a class="wiki_link" href="/14_13"&gt;14/13&lt;/a&gt;, &lt;a class="wiki_link" href="/16_15"&gt;16/15&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;ru&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;m2&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Eb&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;4&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;184.62&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/9_8"&gt;9/8&lt;/a&gt;, &lt;a class="wiki_link" href="/10_9"&gt;10/9&lt;/a&gt;, &lt;a class="wiki_link" href="/11_10"&gt;11/10&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;re&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;M2&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;E&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;5&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;230.77&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/8_7"&gt;8/7&lt;/a&gt;, 15/13&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;ri&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;A2&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;E#&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;6&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;276.92&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/7_6"&gt;7/6&lt;/a&gt;, &lt;a class="wiki_link" href="/13_11"&gt;13/11&lt;/a&gt;, &lt;a class="wiki_link" href="/33_28"&gt;33/28&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;ma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;d3&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Fb&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;7&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;323.08&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/6_5"&gt;6/5&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;me&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;m3&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;F&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;8&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;369.23&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/5_4"&gt;5/4&lt;/a&gt;, &lt;a class="wiki_link" href="/11_9"&gt;11/9&lt;/a&gt;, &lt;a class="wiki_link" href="/16_13"&gt;16/13&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;muh/mi&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;M3&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;F#&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;9&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;415.38&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/9_7"&gt;9/7&lt;/a&gt;, &lt;a class="wiki_link" href="/14_11"&gt;14/11&lt;/a&gt;, &lt;a class="wiki_link" href="/33_26"&gt;33/26&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;maa&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;A3&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Fx&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;10&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;461.54&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/21_16"&gt;21/16&lt;/a&gt;, &lt;a class="wiki_link" href="/13_10"&gt;13/10&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;fe&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;d4&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Gb&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;11&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;507.69&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/4_3"&gt;4/3&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;fa&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;P4&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;G&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;12&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;553.85&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/11_8"&gt;11/8&lt;/a&gt;, &lt;a class="wiki_link" href="/18_13"&gt;18/13&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;fu&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;A4&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;G#&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;13&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;600&lt;span style="color: #ffffff;"&gt;.00&lt;/span&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/7_5"&gt;7/5&lt;/a&gt;, &lt;a class="wiki_link" href="/10_7"&gt;10/7&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;fi/se&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;AA4, dd5&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Gx, Abb&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;14&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;646.15&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/16_11"&gt;16/11&lt;/a&gt;, &lt;a class="wiki_link" href="/13_9"&gt;13/9&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;su&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;d5&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Ab&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;15&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;692.31&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/3_2"&gt;3/2&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;sol&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;P5&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;A&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;16&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;738.46&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/32_21"&gt;32/21&lt;/a&gt;, &lt;a class="wiki_link" href="/20_13"&gt;20/13&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;si&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;A5&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;A#&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;17&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;784.62&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/11_7"&gt;11/7&lt;/a&gt;, &lt;a class="wiki_link" href="/14_9"&gt;14/9&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;leh&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;d6&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Bbb&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;18&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;830.77&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/13_8"&gt;13/8&lt;/a&gt;, &lt;a class="wiki_link" href="/8_5"&gt;8/5&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;le/lu&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;m6&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Bb&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;19&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;876.92&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/5_3"&gt;5/3&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;la&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;M6&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;B&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;20&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;923.08&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/12_7"&gt;12/7&lt;/a&gt;, &lt;a class="wiki_link" href="/22_13"&gt;22/13&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;li&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;A6&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;B#&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;21&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;969.23&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/7_4"&gt;7/4&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;ta&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;d7&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Cb&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;22&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;1015.38&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/9_5"&gt;9/5&lt;/a&gt;, &lt;a class="wiki_link" href="/16_9"&gt;16/9&lt;/a&gt;, &lt;a class="wiki_link" href="/20_11"&gt;20/11&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;te&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;m7&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;C&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;23&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;1061.54&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/11_6"&gt;11/6&lt;/a&gt;, &lt;a class="wiki_link" href="/13_7"&gt;13/7&lt;/a&gt;, &lt;a class="wiki_link" href="/15_8"&gt;15/8&lt;/a&gt;, &lt;a class="wiki_link" href="/24_13"&gt;24/13&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;tu/ti&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;M7&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;C#&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;24&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;1107.69&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/21_11"&gt;21/11&lt;/a&gt;, &lt;a class="wiki_link" href="/25_13"&gt;25/13&lt;/a&gt;, &lt;a class="wiki_link" href="/40_21"&gt;40/21&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;to&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;A7&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Cx&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;25&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;1153.85&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/64_33"&gt;64/33&lt;/a&gt;, &lt;a class="wiki_link" href="/96_49"&gt;96/49&lt;/a&gt;, &lt;a class="wiki_link" href="/35_18"&gt;35/18&lt;/a&gt;, &lt;a class="wiki_link" href="/48_25"&gt;48/25&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;da&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;d8&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Db&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;26&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;1200&lt;span style="color: #ffffff;"&gt;.00&lt;/span&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;2/1&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;do&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;P8&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;D&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-&lt;/table&gt;
-*based on treating 26-EDO as a 13-limit temperament; other approaches are possible.&lt;br /&gt;
+-Igs
-&lt;br /&gt;
-Using &lt;a class="wiki_link" href="/Kite%27s%20color%20notation"&gt;color notation&lt;/a&gt;, qualities can be loosely associated with colors:&lt;br /&gt;
+=Literature=
-&lt;table class="wiki_table"&gt;
+[http://www.ronsword.com Sword, Ron. **Icosihexaphonic Scales for Guitar**. IAAA Press. 2010 - A Guitar-scale thesaurus for 26-EDO.]
-    &lt;tr&gt;
-        &lt;th&gt;quality&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;color&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;monzo format&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;examples&lt;br /&gt;
-&lt;/th&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;diminished&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;blue&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;{a, b, 0, 1}&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;7/6, 7/4&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;minor&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;fourthward white&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;{a, b}, b &amp;lt; -1&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;32/27, 16/9&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&amp;quot;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;green&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;{a, b, -1}&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;6/5, 9/5&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;major&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;yellow&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;{a, b, 1}&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;5/4, 5/3&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&amp;quot;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;fifthward white&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;{a, b}, b &amp;gt; 1&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;9/8, 27/16&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;augmented&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;red&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;{a, b, 0, -1}&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;9/7, 12/7&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-&lt;/table&gt;
-All 26edo chords can be named using conventional methods, expanded to include augmented and diminished 2nd, 3rds, 6ths and 7ths. Spelling certain chords properly may require triple sharps and flats, especially if the tonic is anything other than the 11 keys in the Eb-C# range. Here are the blue, green, yellow and red triads&lt;br /&gt;
+=Compositions=
+[http://soonlabel.com/xenharmonic/archives/3335 Canon 3-in-1 on a ground ‘The tempest’, by Claudi Meneghin]
-&lt;table class="wiki_table"&gt;
+<span style="">[http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Igs/City%20Of%20The%20Asleep%20-%20A%20Time-Yellowed%20Photograph%20of%20Cliffs%20Hangs%20in%20the%20Hall.mp3 A Time-Yellowed Photo of the Cliffs Hangs on the Wall ]</span> by [[IgliashonJones|Igliashon Jones]]
-    &lt;tr&gt;
-        &lt;th&gt;color of the 3rd&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;JI chord&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;notes as edosteps&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;notes of C chord&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;written name&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;spoken name&lt;br /&gt;
-&lt;/th&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;blue&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;6:7:9&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;0-6-15&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;C Ebb G&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;C(b3) or C(d3)&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;C flat-three or C dim-three&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;green&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;10:12:15&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;0-7-15&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;C Eb G&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Cm&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;C minor&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;yellow&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;4:5:6&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;0-8-15&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;C E G&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;C&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;C major or C&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;red&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;14:18:27&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;0-9-15&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;C E# G&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;C(#3) or C(A3)&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;C sharp-three or C aug-three&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-&lt;/table&gt;
-For a more complete list, see &lt;a class="wiki_link" href="https://xenharmonic.wikispaces.com/Ups%20and%20Downs%20Notation#Chord%20names%20in%20other%20EDOs"&gt;Ups and Downs Notation - Chord names in other EDOs&lt;/a&gt;.&lt;br /&gt;
+<span style="">[http://micro.soonlabel.com/gene_ward_smith/Others/Igs/Two%20Pairs%20of%20Socks.mp3 Two Pairs of Socks]</span> by [[IgliashonJones|Igliashon Jones]]
-&lt;br /&gt;
-&lt;!-- ws:start:WikiTextHeadingRule:5:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc2"&gt;&lt;a name="x-Selected just intervals by error"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:5 --&gt;Selected just intervals by error&lt;/h2&gt;
- The following table shows how &lt;a class="wiki_link" href="/Just-24"&gt;some prominent just intervals&lt;/a&gt; are represented in 26edo (ordered by absolute error).&lt;br /&gt;
+[http://www.io.com/%7Ehmiller/midi/26tet.mid Etude in 26-tone equal temperament] <span style="">[http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Herman/26tet.mp3 play]</span> by [[Herman_Miller|Herman Miller]]
-&lt;table class="wiki_table"&gt;
+[http://archive.org/details/UnderTheHeatdome under the heatDome] [http://archive.org/download/UnderTheHeatdome/under_the_heatDome.mp3 play] by [[Jon_Lyle_Smith|Jon Lyle Smith]]
-    &lt;tr&gt;
-        &lt;th&gt;Interval, complement&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;Error (abs., in &lt;a class="wiki_link" href="/cent"&gt;cents&lt;/a&gt;)&lt;br /&gt;
-&lt;/th&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/13_12"&gt;13/12&lt;/a&gt;, &lt;a class="wiki_link" href="/24_13"&gt;24/13&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;0.111&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/8_7"&gt;8/7&lt;/a&gt;, &lt;a class="wiki_link" href="/7_4"&gt;7/4&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;0.405&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/14_11"&gt;14/11&lt;/a&gt;, &lt;a class="wiki_link" href="/11_7"&gt;11/7&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;2.123&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/10_9"&gt;10/9&lt;/a&gt;, &lt;a class="wiki_link" href="/9_5"&gt;9/5&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;2.212&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/11_8"&gt;11/8&lt;/a&gt;, &lt;a class="wiki_link" href="/16_11"&gt;16/11&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;2.528&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/13_10"&gt;13/10&lt;/a&gt;, &lt;a class="wiki_link" href="/20_13"&gt;20/13&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;7.325&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/6_5"&gt;6/5&lt;/a&gt;, &lt;a class="wiki_link" href="/5_3"&gt;5/3&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;7.436&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/18_13"&gt;18/13&lt;/a&gt;, &lt;a class="wiki_link" href="/13_9"&gt;13/9&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;9.536&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/4_3"&gt;4/3&lt;/a&gt;, &lt;a class="wiki_link" href="/3_2"&gt;3/2&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;9.647&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/16_13"&gt;16/13&lt;/a&gt;, &lt;a class="wiki_link" href="/13_8"&gt;13/8&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;9.758&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/7_6"&gt;7/6&lt;/a&gt;, &lt;a class="wiki_link" href="/12_7"&gt;12/7&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;10.052&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/14_13"&gt;14/13&lt;/a&gt;, &lt;a class="wiki_link" href="/13_7"&gt;13/7&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;10.163&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/12_11"&gt;12/11&lt;/a&gt;, &lt;a class="wiki_link" href="/11_6"&gt;11/6&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;12.176&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/13_11"&gt;13/11&lt;/a&gt;, &lt;a class="wiki_link" href="/22_13"&gt;22/13&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;12.287&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/15_11"&gt;15/11&lt;/a&gt;, &lt;a class="wiki_link" href="/22_15"&gt;22/15&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;16.895&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/15_13"&gt;15/13&lt;/a&gt;, &lt;a class="wiki_link" href="/26_15"&gt;26/15&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;16.972&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/5_4"&gt;5/4&lt;/a&gt;, &lt;a class="wiki_link" href="/8_5"&gt;8/5&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;17.083&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/7_5"&gt;7/5&lt;/a&gt;, &lt;a class="wiki_link" href="/10_7"&gt;10/7&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;17.488&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/15_14"&gt;15/14&lt;/a&gt;, &lt;a class="wiki_link" href="/28_15"&gt;28/15&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;19.019&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/9_8"&gt;9/8&lt;/a&gt;, &lt;a class="wiki_link" href="/16_9"&gt;16/9&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;19.295&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/16_15"&gt;16/15&lt;/a&gt;, &lt;a class="wiki_link" href="/15_8"&gt;15/8&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;19.424&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/11_10"&gt;11/10&lt;/a&gt;, &lt;a class="wiki_link" href="/20_11"&gt;20/11&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;19.611&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/9_7"&gt;9/7&lt;/a&gt;, &lt;a class="wiki_link" href="/14_9"&gt;14/9&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;19.699&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;&lt;a class="wiki_link" href="/11_9"&gt;11/9&lt;/a&gt;, &lt;a class="wiki_link" href="/18_11"&gt;18/11&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;21.823&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-&lt;/table&gt;
-&lt;br /&gt;
+[http://danielthompson.blogspot.com/2007/04/new-version-of-organ-study-1.html A New Recording of Organ Study #1] <span style="">[http://www.microtonalmusic.net/audio/organstudyremix26edo.mp3 play]</span> by [[Daniel_Thompson|Daniel Thompson]]
-&lt;!-- ws:start:WikiTextHeadingRule:7:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc3"&gt;&lt;a name="Rank two temperaments"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:7 --&gt;Rank two temperaments&lt;/h1&gt;
- &lt;a class="wiki_link" href="/List%20of%2026et%20rank%20two%20temperaments%20by%20badness"&gt;List of 26et rank two temperaments by badness&lt;/a&gt;&lt;br /&gt;
-&lt;a class="wiki_link" href="/List%20of%20edo-distinct%2026et%20rank%20two%20temperaments"&gt;List of edo-distinct 26et rank two temperaments&lt;/a&gt;&lt;br /&gt;
+<span style="">[http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Bobro/LittleFugueIn26_CBobro.mp3 Little Fugue in 26]</span> by [[Cameron_Bobro|Cameron Bobro]]
-&lt;table class="wiki_table"&gt;
+<span style="">[http://soonlabel.com/xenharmonic/wp-content/uploads/2011/11/26-tone-fugue.mp3 26 tone fugue (unfinished)]</span> by Peter Kosmorsky (based on the melody he was singing in the shower, in orgone, to the presumed confusion of those in earshot)
-    &lt;tr&gt;
-        &lt;th&gt;Periods&lt;br /&gt;
-per octave&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;Generator&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;Temperaments&lt;br /&gt;
-&lt;/th&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;1&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;1\26&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;a class="wiki_link" href="/Quartonic"&gt;Quartonic&lt;/a&gt;/Quarto&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;1&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;3\26&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;a class="wiki_link" href="/Jerome"&gt;Jerome&lt;/a&gt;/&lt;a class="wiki_link" href="/Chromatic%20pairs"&gt;Bleu&lt;/a&gt;/Secund&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;1&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;5\26&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;a class="wiki_link" href="/Cynder"&gt;Cynder&lt;/a&gt;/&lt;a class="wiki_link" href="/Mothra"&gt;Mothra&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;1&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;7\26&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;a class="wiki_link" href="/Superkleismic"&gt;Superkleismic&lt;/a&gt;/&lt;a class="wiki_link" href="/Orgone"&gt;Orgone&lt;/a&gt;/&lt;a class="wiki_link" href="/Shibboleth"&gt;Shibboleth&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;1&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;9\26&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;a class="wiki_link" href="/Roman"&gt;Roman&lt;/a&gt;/Wesley&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;1&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;11\26&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;a class="wiki_link" href="/Meantone"&gt;Meantone&lt;/a&gt;/&lt;a class="wiki_link" href="/Flattone"&gt;Flattone&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;2&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;1\26&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;Elvis&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;2&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;2\26&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;a class="wiki_link" href="/Injera"&gt;Injera&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;2&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;3\26&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;a class="wiki_link" href="/Fifive"&gt;Fifive&lt;/a&gt;/Crepuscular&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;2&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;4\26&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;a class="wiki_link" href="/Unidec"&gt;Unidec&lt;/a&gt;/&lt;a class="wiki_link" href="/Gamelismic%20clan#Unidec-Hendec"&gt;Hendec&lt;/a&gt;/Dubbla&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;2&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;5\26&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;a class="wiki_link" href="/Lemba"&gt;Lemba&lt;/a&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;2&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;6\26&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;a class="wiki_link" href="/Doublewide"&gt;Doublewide&lt;/a&gt;/Cavalier&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;13&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;1\26&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;Triskaidekic&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-&lt;/table&gt;
-&lt;br /&gt;
+<span style="">[http://www.96edo.com/music/micro900607.mp3 Microtonal music in 26-EDO]</span> by [[Shaahin_Mohajeri|Shaahin Mohajeri]]
-&lt;!-- ws:start:WikiTextHeadingRule:9:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc4"&gt;&lt;a name="Rank two temperaments-Hendec in 26et"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:9 --&gt;Hendec in 26et&lt;/h2&gt;
- &lt;a class="wiki_link" href="/Gamelismic%20clan#Unidec-Hendec"&gt;Hendec&lt;/a&gt;, the 13-limit 26&amp;amp;46 temperament with generator ~10/9, concentrates the intervals of greatest accuracy in 26et into the lower ranges of complexity. It has a period of half an octave, with 13/12 reachable by four generators, 8/7 by two, 14/11 by one, 10/9 by one, and 11/8 by three. All of these are tuned to within 2.5 cents of accuracy.&lt;br /&gt;
-&lt;br /&gt;
-&lt;!-- ws:start:WikiTextHeadingRule:11:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc5"&gt;&lt;a name="Commas"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:11 --&gt;Commas&lt;/h1&gt;
-et tempers out the following commas. (Note: This assumes the val &amp;lt; 26 41 60 73 90 96 |.)&lt;br /&gt;
+<span style="">[http://micro.soonlabel.com/gene_ward_smith/Others/Curley/Zach%20Curley%20-%20Chiapas%20Palenque.mp3 Chiapas Palenque]</span> by [[Zach_Curley|Zach Curley]]
-&lt;table class="wiki_table"&gt;
+<span style="">[http://micro.soonlabel.com/gene_ward_smith/Others/Curley/Zach%20Curley%20-%20Injera%20Jam.mp3 Injera Jam]</span> by [[Zach_Curley|Zach Curley]]
-    &lt;tr&gt;
-        &lt;th&gt;Ratio&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;Monzo&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;Size (Cents)&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;Name 1&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;Name 2&lt;br /&gt;
-&lt;/th&gt;
-        &lt;th&gt;Name 3&lt;br /&gt;
-&lt;/th&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;81/80&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| -4 4 -1 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;21.51&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Syntonic Comma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Didymos Comma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Meantone Comma&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;5696703/5695946&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| -17 62 -35 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;0.23&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Senior&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;525/512&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| -9 1 2 1 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;43.41&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Avicennma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Avicenna's Enharmonic Diesis&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;50/49&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| 1 0 2 -2 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;34.98&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Tritonic Diesis&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Jubilisma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;875/864&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| -5 -3 3 1 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;21.90&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Keema&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;4000/3969&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| 5 -4 3 -2 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;13.47&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Octagar&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;1728/1715&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| 6 3 -1 -3 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;13.07&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Orwellisma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Orwell Comma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;1029/1024&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| -10 1 0 3 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;8.43&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Gamelisma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;321489/320000&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| -9 8 -4 2 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;8.04&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Varunisma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;1065875/1063543&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| -26 -1 1 9 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;3.79&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Wadisma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;4375/4374&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| -1 -7 4 1 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;0.40&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Ragisma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;99/98&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| -1 2 0 -2 1 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;17.58&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Mothwellsma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;100/99&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| 2 -2 2 0 -1 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;17.40&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Ptolemisma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;105/104&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| -3 1 1 1 0 -1 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;16.57&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Animist&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;65536/65219&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| 16 0 0 -2 -3 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;8.39&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Orgonisma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;385/384&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| -7 -1 1 1 1 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;4.50&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Keenanisma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;441/440&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| -3 2 -1 2 -1 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;3.93&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Werckisma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;3025/3024&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| -4 -3 2 -1 2 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;0.57&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Lehmerisma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td style="text-align: center;"&gt;9801/9800&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: left;"&gt;| -3 4 -2 -2 2 &amp;gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: right;"&gt;0.18&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Kalisma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;Gauss' Comma&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-&lt;/table&gt;
-&lt;!-- ws:start:WikiTextHeadingRule:13:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc6"&gt;&lt;a name="Orgone Temperament"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:13 --&gt;&lt;a class="wiki_link" href="/Orgonia"&gt;Orgone Temperament&lt;/a&gt;&lt;/h1&gt;
+[http://micro.soonlabel.com/gene_ward_smith/Others/Curley/Zach%20Curley%20-%20Guitar%20Serenade%20in%20Q%20Major.mp3 Guitar Serenade in Q Major] by [[Zach_Curley|Zach Curley]]
- &lt;br /&gt;
-&lt;a class="wiki_link" href="/Andrew%20Heathwaite"&gt;Andrew Heathwaite&lt;/a&gt; first proposed orgone temperament to take advantage of 26edo's excellent 11 and 7 approximations. 7 degrees of 26edo is a wide minor third of approximately 323.077 cents, and that interval taken as a generator produces 7-tone and 11-tone MOS scales:&lt;br /&gt;
-&lt;br /&gt;
-The 7-tone scale in degrees-in-between: 5 2 5 2 5 2 5. &lt;a class="wiki_link" href="/MOSScales"&gt;MOS&lt;/a&gt; of type &lt;a class="wiki_link" href="/4L%203s"&gt;4L 3s (mish)&lt;/a&gt;.&lt;br /&gt;
-The 7-tone scale in cents: 0 231 323 554 646 877 969 1200.&lt;br /&gt;
-&lt;br /&gt;
-The 11-tone scale in degrees-in-between: 2 3 2 2 3 2 3 2 2 3 2. &lt;a class="wiki_link" href="/MOSScales"&gt;MOS&lt;/a&gt; of type &lt;a class="wiki_link" href="/4L%207s"&gt;4L 7s&lt;/a&gt;.&lt;br /&gt;
-The 11-tone scale in cents: 0 92 231 323 415 554 646 785 877 969 1108 1200.&lt;br /&gt;
-&lt;br /&gt;
-The primary triad for orgone temperament is 8:11:14 and its subharmonic inversion, which these scales have in abundance. 2g approximates &lt;a class="wiki_link" href="/16_11"&gt;16:11&lt;/a&gt; and 3g approximates &lt;a class="wiki_link" href="/7_4"&gt;7:4&lt;/a&gt; (and I would call that the definition of Orgone Temperament). That also implies that g approximates the difference between 7:4 and 16:11, which is 77:64, about 320.1 cents.&lt;br /&gt;
-&lt;br /&gt;
-&lt;a class="wiki_link" href="/37edo"&gt;37edo&lt;/a&gt; is another orgone tuning, and &lt;a class="wiki_link" href="/89edo"&gt;89edo&lt;/a&gt; is better even than 26. If we take 11 and 26 to be the edges of the Orgone Spectrum, we may fill in the rest of the spectrum thus:&lt;br /&gt;
-&lt;br /&gt;
+[http://midiguru.wordpress.com/2013/01/06/public-rituals/ Public Rituals « Jim Aikin's Oblong Blob] “The Triumphal Procession of Nebuchadnezzar“
-&lt;table class="wiki_table"&gt;
+[http://www.unfretted.com/microtonal/melopoeia-project-26-edo-album-based-on-tolkeins-silmarillion-ainulindale/ Melopœia Project – 26 EDO album based on Tolkein’s Silmarillion – Ainulindalë – Unfretted]
-    &lt;tr&gt;
-        &lt;td&gt;3\11&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;19\70&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;16\59&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;29\107&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;13\48&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;36\133&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;23\85&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;33\122&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;10\37&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;37\137&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;27\100&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;44\163&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;17\63&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;41\152&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;24\89&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;31\115&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-    &lt;tr&gt;
-        &lt;td&gt;7\26&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-        &lt;td&gt;&lt;br /&gt;
-&lt;/td&gt;
-    &lt;/tr&gt;
-&lt;/table&gt;
-&lt;br /&gt;
+[http://micro.soonlabel.com/26edo/20161224_26edo_wing.mp3 Morpheous Wing in 26 edo] by [[Chris_Vaisvil|Chris Vaisvil]]      [[Category:26edo]]
-Orgone has a minimax tuning which sharpens both 7 and 11 by 1/5 of an orgonisma, or 1.679 cents. This makes the generator g a 77/64 sharp by 2/5 of the orgonisma. From this we may conclude that 24/89 or 31/115 would be reasonable alternatives to the 7/26 generator.&lt;br /&gt;
+[[Category:edo]]
-&lt;br /&gt;
+[[Category:listen]]
-&lt;!-- ws:start:WikiTextLocalImageRule:1325:&amp;lt;img src=&amp;quot;/file/view/orgone_heptatonic.jpg/155606933/orgone_heptatonic.jpg&amp;quot; alt=&amp;quot;&amp;quot; title=&amp;quot;&amp;quot; /&amp;gt; --&gt;&lt;img src="/file/view/orgone_heptatonic.jpg/155606933/orgone_heptatonic.jpg" alt="orgone_heptatonic.jpg" title="orgone_heptatonic.jpg" /&gt;&lt;!-- ws:end:WikiTextLocalImageRule:1325 --&gt;&lt;br /&gt;
+[[Category:theory]]
-&lt;br /&gt;
+[[Category:todo:unify_precision]]
-&lt;br /&gt;
+[[Category:twentuning]]
-&lt;!-- ws:start:WikiTextHeadingRule:15:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc7"&gt;&lt;a name="Additional Scalar Bases Available in 26-EDO:"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:15 --&gt;Additional Scalar Bases Available in 26-EDO:&lt;/h1&gt;
- Since the perfect 5th in 26-EDO spans 15 degrees, it can be divided into three equal parts (each approximately an 8/7) as well as five equal parts (each approximately a 13/12). The former approach produces MOS at 1L+4s, 5L+1s, and 5L+6s (5 5 5 5 6, 5 5 5 5 5 1, and 4 1 4 1 4 1 4 1 4 1 1 respectively), and is excellent for 4:6:7 triads. The latter produces MOS at 1L+7s and 8L+1s (3 3 3 3 3 3 3 5 and 3 3 3 3 3 3 3 3 2 respectively), and is fairly well-supplied with 4:6:7:11:13 pentads. It also works well for more conventional (though further from Just) 6:7:9 triads, as well as 4:5:6 triads that use the worse mapping for 5 (making 5/4 the 415.38-cent interval).&lt;br /&gt;
-&lt;br /&gt;
--Igs&lt;br /&gt;
-&lt;br /&gt;
-&lt;!-- ws:start:WikiTextHeadingRule:17:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc8"&gt;&lt;a name="Literature"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:17 --&gt;Literature&lt;/h1&gt;
- &lt;br /&gt;
-&lt;a class="wiki_link_ext" href="http://www.ronsword.com" rel="nofollow"&gt;Sword, Ron. **Icosihexaphonic Scales for Guitar**. IAAA Press. 2010 - A Guitar-scale thesaurus for 26-EDO.&lt;/a&gt;&lt;br /&gt;
-&lt;br /&gt;
-&lt;!-- ws:start:WikiTextHeadingRule:19:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc9"&gt;&lt;a name="Compositions"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:19 --&gt;Compositions&lt;/h1&gt;
- &lt;br /&gt;
-&lt;a class="wiki_link_ext" href="http://soonlabel.com/xenharmonic/archives/3335" rel="nofollow"&gt;Canon 3-in-1 on a ground ‘The tempest’, by Claudi Meneghin&lt;/a&gt;&lt;br /&gt;
-&lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;&lt;a class="wiki_link_ext" href="http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Igs/City%20Of%20The%20Asleep%20-%20A%20Time-Yellowed%20Photograph%20of%20Cliffs%20Hangs%20in%20the%20Hall.mp3" rel="nofollow"&gt;A Time-Yellowed Photo of the Cliffs Hangs on the Wall &lt;/a&gt;&lt;/span&gt; by &lt;a class="wiki_link" href="/IgliashonJones"&gt;Igliashon Jones&lt;/a&gt;&lt;br /&gt;
-&lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;&lt;a class="wiki_link_ext" href="http://micro.soonlabel.com/gene_ward_smith/Others/Igs/Two%20Pairs%20of%20Socks.mp3" rel="nofollow"&gt;Two Pairs of Socks&lt;/a&gt;&lt;/span&gt; by &lt;a class="wiki_link" href="/IgliashonJones"&gt;Igliashon Jones&lt;/a&gt;&lt;br /&gt;
-&lt;a class="wiki_link_ext" href="http://www.io.com/%7Ehmiller/midi/26tet.mid" rel="nofollow"&gt;Etude in 26-tone equal temperament&lt;/a&gt; &lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;&lt;a class="wiki_link_ext" href="http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Herman/26tet.mp3" rel="nofollow"&gt;play&lt;/a&gt;&lt;/span&gt; by &lt;a class="wiki_link" href="/Herman%20Miller"&gt;Herman Miller&lt;/a&gt;&lt;br /&gt;
-&lt;a class="wiki_link_ext" href="http://archive.org/details/UnderTheHeatdome" rel="nofollow"&gt;under the heatDome&lt;/a&gt; &lt;a class="wiki_link_ext" href="http://archive.org/download/UnderTheHeatdome/under_the_heatDome.mp3" rel="nofollow"&gt;play&lt;/a&gt; by &lt;a class="wiki_link" href="/Jon%20Lyle%20Smith"&gt;Jon Lyle Smith&lt;/a&gt;&lt;br /&gt;
-&lt;a class="wiki_link_ext" href="http://danielthompson.blogspot.com/2007/04/new-version-of-organ-study-1.html" rel="nofollow"&gt;A New Recording of Organ Study #1&lt;/a&gt; &lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;&lt;a class="wiki_link_ext" href="http://www.microtonalmusic.net/audio/organstudyremix26edo.mp3" rel="nofollow"&gt;play&lt;/a&gt;&lt;/span&gt; by &lt;a class="wiki_link" href="/Daniel%20Thompson"&gt;Daniel Thompson&lt;/a&gt;&lt;br /&gt;
-&lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;&lt;a class="wiki_link_ext" href="http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Bobro/LittleFugueIn26_CBobro.mp3" rel="nofollow"&gt;Little Fugue in 26&lt;/a&gt;&lt;/span&gt; by &lt;a class="wiki_link" href="/Cameron%20Bobro"&gt;Cameron Bobro&lt;/a&gt;&lt;br /&gt;
-&lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;&lt;a class="wiki_link_ext" href="http://soonlabel.com/xenharmonic/wp-content/uploads/2011/11/26-tone-fugue.mp3" rel="nofollow"&gt;26 tone fugue (unfinished)&lt;/a&gt;&lt;/span&gt; by Peter Kosmorsky (based on the melody he was singing in the shower, in orgone, to the presumed confusion of those in earshot)&lt;br /&gt;
-&lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;&lt;a class="wiki_link_ext" href="http://www.96edo.com/music/micro900607.mp3" rel="nofollow"&gt;Microtonal music in 26-EDO&lt;/a&gt;&lt;/span&gt; by &lt;a class="wiki_link" href="/Shaahin%20Mohajeri"&gt;Shaahin Mohajeri&lt;/a&gt;&lt;br /&gt;
-&lt;!-- ws:start:WikiTextMediaRule:0:&amp;lt;img src=&amp;quot;https://www.wikispaces.com/site/embedthumbnail/custom/11317210?h=0&amp;amp;w=0&amp;quot; class=&amp;quot;WikiMedia WikiMediaCustom&amp;quot; id=&amp;quot;wikitext@@media@@type=&amp;amp;quot;custom&amp;amp;quot; key=&amp;amp;quot;11317210&amp;amp;quot;&amp;quot; title=&amp;quot;Custom Media&amp;quot;/&amp;gt; --&gt;&lt;script type="text/javascript" src="http://mediaplayer.yahoo.com/js"&gt;
-&lt;/script&gt;&lt;!-- ws:end:WikiTextMediaRule:0 --&gt;&lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;&lt;a class="wiki_link_ext" href="http://micro.soonlabel.com/gene_ward_smith/Others/Curley/Zach%20Curley%20-%20Chiapas%20Palenque.mp3" rel="nofollow"&gt;Chiapas Palenque&lt;/a&gt;&lt;/span&gt; by &lt;a class="wiki_link" href="/Zach%20Curley"&gt;Zach Curley&lt;/a&gt;&lt;br /&gt;
-&lt;span class="ywp-page-play-pause ywp-page-audio ywp-link-hover ywp-page-img-link"&gt;&lt;a class="wiki_link_ext" href="http://micro.soonlabel.com/gene_ward_smith/Others/Curley/Zach%20Curley%20-%20Injera%20Jam.mp3" rel="nofollow"&gt;Injera Jam&lt;/a&gt;&lt;/span&gt; by &lt;a class="wiki_link" href="/Zach%20Curley"&gt;Zach Curley&lt;/a&gt;&lt;br /&gt;
-&lt;a class="wiki_link_ext" href="http://micro.soonlabel.com/gene_ward_smith/Others/Curley/Zach%20Curley%20-%20Guitar%20Serenade%20in%20Q%20Major.mp3" rel="nofollow"&gt;Guitar Serenade in Q Major&lt;/a&gt; by &lt;a class="wiki_link" href="/Zach%20Curley"&gt;Zach Curley&lt;/a&gt;&lt;br /&gt;
-&lt;a class="wiki_link_ext" href="http://midiguru.wordpress.com/2013/01/06/public-rituals/" rel="nofollow"&gt;Public Rituals « Jim Aikin's Oblong Blob&lt;/a&gt; “The Triumphal Procession of Nebuchadnezzar“&lt;br /&gt;
-&lt;a class="wiki_link_ext" href="http://www.unfretted.com/microtonal/melopoeia-project-26-edo-album-based-on-tolkeins-silmarillion-ainulindale/" rel="nofollow"&gt;Melopœia Project – 26 EDO album based on Tolkein’s Silmarillion – Ainulindalë – Unfretted&lt;/a&gt;&lt;br /&gt;
-&lt;a class="wiki_link_ext" href="http://micro.soonlabel.com/26edo/20161224_26edo_wing.mp3" rel="nofollow"&gt;Morpheous Wing in 26 edo&lt;/a&gt; by &lt;a class="wiki_link" href="/Chris%20Vaisvil"&gt;Chris Vaisvil&lt;/a&gt;&lt;/body&gt;&lt;/html&gt;</pre></div>

26edo: Difference between revisions

Revision as of 00:00, 17 July 2018

Structure

Intervals

Selected just intervals by error

Rank two temperaments

Hendec in 26et

Commas

Orgone Temperament

Additional Scalar Bases Available in 26-EDO:

Literature

Compositions

Navigation menu

Search