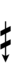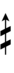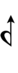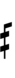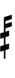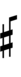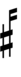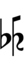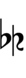65edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older editNewer edit →
VisualWikitext
Contribution (talk | contribs)
autopatrolled
2,880 edits
No edit summary
ArrowHead294 (talk | contribs)
14,512 edits
mNo edit summary
Line 5: Line 5:
65et can be characterized as the temperament which [[tempering out|tempers out]] 32805/32768 ([[schisma]]), 78732/78125 ([[sensipent comma]]), 393216/390625 ([[würschmidt comma]]), and {{monzo| -13 17 -6 }} ([[graviton]]). In the [[7-limit]], there are two different maps; the first is {{val| 65 103 151 '''182''' }} (65), tempering out [[126/125]], [[245/243]] and [[686/675]], so that it [[support]]s [[sensi]], and the second is {{val| 65 103 151 '''183''' }} (65d), tempering out [[225/224]], [[3125/3087]], [[4000/3969]] and [[5120/5103]], so that it supports [[garibaldi]]. In both cases, the tuning privileges the [[5-limit]] over the 7-limit, as the 5-limit of 65 is quite accurate. The same can be said for the two different versions of 7-limit [[würschmidt]] temperament (wurschmidt and worschmidt) these two mappings provide.
65et can be characterized as the temperament which [[tempering out|tempers out]] 32805/32768 ([[schisma]]), 78732/78125 ([[sensipent comma]]), 393216/390625 ([[würschmidt comma]]), and {{monzo| -13 17 -6 }} ([[graviton]]). In the [[7-limit]], there are two different maps; the first is {{val| 65 103 151 '''182''' }} (65), tempering out [[126/125]], [[245/243]] and [[686/675]], so that it [[support]]s [[sensi]], and the second is {{val| 65 103 151 '''183''' }} (65d), tempering out [[225/224]], [[3125/3087]], [[4000/3969]] and [[5120/5103]], so that it supports [[garibaldi]]. In both cases, the tuning privileges the [[5-limit]] over the 7-limit, as the 5-limit of 65 is quite accurate. The same can be said for the two different versions of 7-limit [[würschmidt]] temperament (wurschmidt and worschmidt) these two mappings provide.


65edo approximates the intervals [[3/2]], [[5/4]], [[11/8]], [[19/16]], [[23/16]], [[31/16]] and [[47/32]] well, so that it does a good job representing the 2.3.5.11.19.23.31.47 [[just intonation subgroup]]. To this one may want to add [[17/16]], [[29/16]] and [[43/32]], giving the [[47-limit]] no-7's no-13's no-37's no-41's subgroup 2.3.5.11.17.19.23.29.31.43.47. In this sense it is a tuning of [[schismic]]/[[nestoria]] that focuses on the very primes that [[53edo]] neglects and that instead elegantly connects primes 7, 13, 37 and 41 to nestoria. Also of interest is the [[19-limit]] [[k*N subgroups|2*65 subgroup]] 2.3.5.49.11.91.119.19, on which 65 has the same tuning and commas as the [[zeta]] edo [[130edo]].
65edo approximates the intervals [[3/2]], [[5/4]], [[11/8]], [[19/16]], [[23/16]], [[31/16]] and [[47/32]] well, so that it does a good job representing the 2.3.5.11.19.23.31.47 [[just intonation subgroup]]. To this one may want to add [[17/16]], [[29/16]] and [[43/32]], giving the [[47-limit]] no-7's no-13's no-37's no-41's subgroup 2.3.5.11.17.19.23.29.31.43.47. In this sense it is a tuning of [[schismic]]/[[nestoria]] that focuses on the very primes that [[53edo]] neglects and that instead elegantly connects primes 7, 13, 37, and 41 to nestoria. Also of interest is the [[19-limit]] [[k*N subgroups|2*65 subgroup]] 2.3.5.49.11.91.119.19, on which 65 has the same tuning and commas as the [[zeta]] edo [[130edo]].


=== Prime harmonics ===
=== Prime harmonics ===
Line 20: Line 20:
! #
! #
! [[Cent]]s
! [[Cent]]s
! Approximate ratios*
! Approximate ratios<ref group="note">{{sg|limit=2.3.5.11.13/7.17.19.23.29.31.47 subgroup}}</ref>
! colspan="2" | [[Ups and downs notation]]
! colspan="2" | [[Ups and downs notation]]
|-
|-
Line 419: Line 419:
| D
| D
|}
|}
<nowiki />* {{sg|limit=2.3.5.11.13/7.17.19.23.29.31.47 subgroup}}


== Notation ==
== Notation ==
=== Ups and downs notation ===
Using [[Helmholtz–Ellis]] accidentals, 65edo can also be notated using [[ups and downs notation]]:
{{Sharpness-sharp6}}


===Sagittal notation===
In some cases, certain notes may be best notated using semi- and sesquisharps and flats with arrows:
{{Sharpness-sharp6-qt}}
 
=== Ivan Wyschnegradsky's notation ===
Since a sharp raises by six steps, Wyschnegradsky accidentals borrowed from [[72edo]] can also be used:
 
{{sharpness-sharp6-iw}}
 
=== Sagittal notation ===
This notation uses the same sagittal sequence as EDOs [[72edo#Sagittal notation|72]] and [[79edo#Sagittal notation|79]].
This notation uses the same sagittal sequence as EDOs [[72edo#Sagittal notation|72]] and [[79edo#Sagittal notation|79]].
====Evo flavor====


==== Evo flavor ====
<imagemap>
<imagemap>
File:65-EDO_Evo_Sagittal.svg
File:65-EDO_Evo_Sagittal.svg
Line 438: Line 448:
</imagemap>
</imagemap>


====Revo flavor====
==== Revo flavor ====
 
<imagemap>
<imagemap>
File:65-EDO_Revo_Sagittal.svg
File:65-EDO_Revo_Sagittal.svg
Line 451: Line 460:
</imagemap>
</imagemap>


====Evo-SZ flavor====
==== Evo-SZ flavor ====
 
<imagemap>
<imagemap>
File:65-EDO_Evo-SZ_Sagittal.svg
File:65-EDO_Evo-SZ_Sagittal.svg
Line 486: Line 494:
| 32805/32768, 78732/78125
| 32805/32768, 78732/78125
| {{mapping| 65 103 151 }}
| {{mapping| 65 103 151 }}
| &minus;0.110
| −0.110
| 0.358
| 0.358
| 1.94
| 1.94
Line 493: Line 501:
| 243/242, 4000/3993, 5632/5625
| 243/242, 4000/3993, 5632/5625
| {{mapping| 65 103 151 225 }}
| {{mapping| 65 103 151 225 }}
| &minus;0.266
| −0.266
| 0.410
| 0.410
| 2.22
| 2.22
Line 577: Line 585:


== Zeta properties ==
== Zeta properties ==
===Zeta peak index===
=== Zeta peak index ===
{| class="wikitable"
{| class="wikitable"
! colspan="3" |Tuning
! colspan="3" |Strength
! colspan="2" |Closest EDO
! colspan="2" |Integer limit
|-
|-
!ZPI
! colspan="3" | Tuning
!Steps per octave
! colspan="3" | Strength
!Step size (cents)
! colspan="2" | Closest EDO
!Height
! colspan="2" | Integer limit
!Integral
|-
!Gap
! ZPI
!EDO
! Steps per octave
!Octave (cents)
! Step size (cents)
!Consistent
! Height
!Distinct
! Integral
! Gap
! EDO
! Octave (cents)
! Consistent
! Distinct
|-
|-
|[[334zpi]]
| [[334zpi]]
|65.0158450885860
| 65.0158450885860
|18.4570391781413
| 18.4570391781413
|7.813349
| 7.813349
|1.269821
| 1.269821
|16.514861
| 16.514861
|65edo
| 65edo
|1199.70754657919
| 1199.70754657919
|6
| 6
|6
| 6
|}
|}
== Scales ==
== Scales ==
* Amulet{{idiosyncratic}}, (approximated from [[25edo]], subset of [[würschmidt]]): 5 3 5 5 3 5 12 5 5 3 5 12 5
* Amulet{{idiosyncratic}}, (approximated from [[25edo]], subset of [[würschmidt]]): 5 3 5 5 3 5 12 5 5 3 5 12 5
Line 614: Line 624:
== Instruments ==
== Instruments ==
[[Lumatone mapping for 65edo]]
[[Lumatone mapping for 65edo]]
== Notes ==
<references group="note" />


[[Category:Listen]]
[[Category:Listen]]

Revision as of 02:21, 19 January 2025

← 64edo 65edo 66edo →
Prime factorization 5 × 13
Step size 18.4615 ¢ 
Fifth 38\65 (701.538 ¢)
Semitones (A1:m2) 6:5 (110.8 ¢ : 92.31 ¢)
Consistency limit 5
Distinct consistency limit 5

Template:EDO intro

Theory

65et can be characterized as the temperament which tempers out 32805/32768 (schisma), 78732/78125 (sensipent comma), 393216/390625 (würschmidt comma), and [-13 17 -6⟩ (graviton). In the 7-limit, there are two different maps; the first is ⟨65 103 151 182] (65), tempering out 126/125, 245/243 and 686/675, so that it supports sensi, and the second is ⟨65 103 151 183] (65d), tempering out 225/224, 3125/3087, 4000/3969 and 5120/5103, so that it supports garibaldi. In both cases, the tuning privileges the 5-limit over the 7-limit, as the 5-limit of 65 is quite accurate. The same can be said for the two different versions of 7-limit würschmidt temperament (wurschmidt and worschmidt) these two mappings provide.

65edo approximates the intervals 3/2, 5/4, 11/8, 19/16, 23/16, 31/16 and 47/32 well, so that it does a good job representing the 2.3.5.11.19.23.31.47 just intonation subgroup. To this one may want to add 17/16, 29/16 and 43/32, giving the 47-limit no-7's no-13's no-37's no-41's subgroup 2.3.5.11.17.19.23.29.31.43.47. In this sense it is a tuning of schismic/nestoria that focuses on the very primes that 53edo neglects and that instead elegantly connects primes 7, 13, 37, and 41 to nestoria. Also of interest is the 19-limit 2*65 subgroup 2.3.5.49.11.91.119.19, on which 65 has the same tuning and commas as the zeta edo 130edo.

Prime harmonics

Approximation of prime harmonics in 65edo
Harmonic 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47
Error Absolute (¢) +0.00 -0.42 +1.38 -8.83 +2.53 +8.70 +5.81 -2.13 -0.58 +4.27 -0.42 +7.12 -4.45 +5.41 -0.89
Relative (%) +0.0 -2.3 +7.5 -47.8 +13.7 +47.1 +31.5 -11.5 -3.2 +23.1 -2.3 +38.6 -24.1 +29.3 -4.8
Steps
(reduced) 		65
(0) 		103
(38) 		151
(21) 		182
(52) 		225
(30) 		241
(46) 		266
(6) 		276
(16) 		294
(34) 		316
(56) 		322
(62) 		339
(14) 		348
(23) 		353
(28) 		361
(36)

Subsets and supersets

65edo contains 13edo as a subset. The offset between a just perfect fifth at 702 cents and the 13edo superfifth at 738.5 cents, is approximately 2 degrees of 65edo. Therefore, an instrument fretted to 13edo, with open strings tuned to 3-limit intervals such as 4/3, 3/2, 9/8, 16/9 etc, will approximate a subset of 65edo. For an example of this, see Andrew Heathwaite's composition Rubble: a Xenuke Unfolded.

130edo, which doubles its, corrects its approximation to harmonics 7 and 13.

Intervals

# Cents Approximate ratios[note 1] Ups and downs notation
0 0.00 1/1 P1 D
1 18.46 81/80, 88/87, 93/92, 94/93, 95/94, 96/95, 100/99, 121/120, 115/114, 116/115, 125/124 ^1 ^D
2 36.92 45/44, 46/45, 47/46, 48/47, 55/54, 128/125 ^^1 ^^D
3 55.38 30/29, 31/30, 32/31, 33/32, 34/33 vvm2 vvEb
4 73.85 23/22, 24/23, 25/24, 47/45 vm2 vEb
5 92.31 18/17, 19/18, 20/19, 58/55, 135/128, 256/243 m2 Eb
6 110.77 16/15, 17/16, 33/31 A1/^m2 D#/^Eb
7 129.23 14/13, 27/25, 55/51 v~2 ^^Eb
8 147.69 12/11, 25/23 ~2 vvvE
9 166.15 11/10, 32/29 ^~2 vvE
10 184.62 10/9, 19/17 vM2 vE
11 203.08 9/8, 64/57 M2 E
12 221.54 17/15, 25/22, 33/29, 58/51 ^M2 ^E
13 240.00 23/20, 31/27, 38/33, 54/47, 55/48 ^^M2 ^^E
14 258.46 22/19, 29/25, 36/31, 64/55 vvm3 vvF
15 276.92 20/17, 27/23, 34/29, 75/64 vm3 vF
16 295.38 19/16, 32/27 m3 F
17 313.85 6/5, 55/46 ^m3 ^F
18 332.31 23/19, 40/33 v~3 ^^F
19 350.77 11/9, 27/22, 38/31 ~3 ^^^F
20 369.23 26/21, 47/38, 68/55 ^~3 vvF#
21 387.69 5/4, 64/51 vM3 vF#
22 406.15 19/15, 24/19, 29/23, 34/27, 81/64 M3 F#
23 424.62 23/18, 32/25 ^M3 ^F#
24 443.08 22/17, 31/24, 40/31, 128/99 ^^M3 ^^F#
25 461.54 30/23, 47/36, 72/55 vv4 vvG
26 480.00 29/22, 33/25, 62/47 v4 vG
27 498.46 4/3 P4 G
28 516.92 23/17, 27/20, 31/23 ^4 ^G
29 535.38 15/11, 34/25, 64/47 v~4 ^^G
30 553.85 11/8, 40/29, 62/45 ~4 ^^^G
31 572.31 25/18, 32/23 ^~4/vd5 vvG#/vAb
32 590.77 24/17, 31/22, 38/27, 45/32 vA4/d5 vG#/Ab
33 609.23 17/12, 27/19, 44/31, 64/45 A4/^d5 G#/^Ab
34 627.69 36/25, 23/16 ^A4/v~5 ^G#/^^Ab
35 646.15 16/11, 29/20, 45/31 ~5 vvvA
36 664.62 22/15, 25/17, 47/32 ^~5 vvA
37 683.08 34/23, 40/27, 46/31 v5 vA
38 701.54 3/2 P5 A
39 720.00 44/29, 50/33, 47/31 ^5 ^A
40 738.46 23/15, 55/36, 72/47 ^^5 ^^A
41 756.92 17/11, 48/31, 31/20, 99/64 vvm6 vvBb
42 775.38 25/16, 36/23 vm6 vBb
43 793.85 19/12, 27/17, 30/19, 46/29, 128/81 m6 Bb
44 812.31 8/5, 51/32 ^m6 ^Bb
45 830.77 21/13, 55/34, 76/47 v~6 ^^Bb
46 849.23 18/11, 31/19, 44/27 ~6 vvvB
47 867.69 33/20, 38/23 ^~6 vvB
48 886.15 5/3, 92/55 vM6 vB
49 904.62 27/16, 32/19 M6 B
50 923.08 17/10, 29/17, 46/27, 128/75 ^M6 ^B
51 941.54 19/11, 31/18, 50/29, 55/32 ^^M6 ^^B
52 960.00 33/19, 40/23, 47/27, 54/31, 96/55 vvm7 vvC
53 978.46 30/17, 44/25, 51/29, 58/33 vm7 vC
54 996.92 16/9, 57/32 m7 C
55 1015.38 9/5, 34/19 ^m7 ^C
56 1033.85 20/11, 29/16 v~7 ^^C
57 1052.31 11/6, 46/25 ~7 ^^^C
58 1070.77 13/7, 50/27, 102/55 ^~7 vvC#
59 1089.23 15/8, 32/17, 62/33 vM7 vC#
60 1107.69 17/9, 19/10, 36/19, 55/29, 243/128, 256/135 M7 C#
61 1126.15 23/12, 44/23, 48/25, 90/47 ^M7 ^C#
62 1144.62 29/15, 31/16, 33/17, 60/31, 64/33 ^^M7 ^^C#
63 1163.08 45/23, 47/24, 88/45, 92/47, 108/55, 125/64 vv8 vvD
64 1181.54 87/55, 93/47, 95/48, 99/50, 115/58, 160/81, 184/93, 188/95, 228/115, 240/121, 248/125 v8 vD
65 1200.00 2/1 P8 D

Notation

Ups and downs notation

Using Helmholtz–Ellis accidentals, 65edo can also be notated using ups and downs notation:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Sharp symbol  
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
Flat symbol  
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 

In some cases, certain notes may be best notated using semi- and sesquisharps and flats with arrows:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13
Sharp symbol
 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
Flat symbol  
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 

Ivan Wyschnegradsky's notation

Since a sharp raises by six steps, Wyschnegradsky accidentals borrowed from 72edo can also be used:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13
Sharp symbol
 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 
  
 		 
Flat symbol  
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 

Sagittal notation

This notation uses the same sagittal sequence as EDOs 72 and 79.

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation81/8064/6333/32

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation81/8064/6333/32

Evo-SZ flavor

Sagittal notationPeriodic table of EDOs with sagittal notation81/8064/6333/32

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3 [-103 65⟩ [⟨65 103]] +0.131 0.131 0.71
2.3.5 32805/32768, 78732/78125 [⟨65 103 151]] −0.110 0.358 1.94
2.3.5.11 243/242, 4000/3993, 5632/5625 [⟨65 103 151 225]] −0.266 0.410 2.22

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods
per 8ve 		Generator* Cents* Associated
ratio* 		Temperament
1 3\65 55.38 33/32 Escapade
1 9\65 166.15 11/10 Squirrel etc.
1 12\65 221.54 25/22 Hemisensi
1 19\65 350.77 11/9 Karadeniz
1 21\65 387.69 5/4 Würschmidt
1 24\65 443.08 162/125 Sensipent
1 27\65 498.46 4/3 Helmholtz / nestoria / photia
1 28\65 516.92 27/20 Larry
5 20\65
(6\65) 		369.23
(110.77) 		99/80
(16/15) 		Quintosec
5 27\65
(1\65) 		498.46
(18.46) 		4/3
(81/80) 		Pental
5 30\65
(4\65) 		553.85
(73.85) 		11/8
(25/24) 		Countdown

* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct

Zeta properties

Zeta peak index

Tuning Strength Closest EDO Integer limit
ZPI Steps per octave Step size (cents) Height Integral Gap EDO Octave (cents) Consistent Distinct
334zpi 65.0158450885860 18.4570391781413 7.813349 1.269821 16.514861 65edo 1199.70754657919 6 6

Scales

Instruments

Lumatone mapping for 65edo

Notes

  1. ↑ Based on treating 65edo as a 2.3.5.11.13/7.17.19.23.29.31.47 subgroup temperament; other approaches are also possible.
Retrieved from "https://en.xen.wiki/index.php?title=65edo&oldid=177040"