24edo: Difference between revisions
m Moved the "24edo tetrachords" link from "see also" to its own subheading, to make the formatting consistent with the "24edo modes" link. Because "24edo tetrachords" was the only content in the "see also" section, I removed that now-empty section. |
m Tidying up formatting. |
||
| Line 9: | Line 9: | ||
{{Wikipedia|Quarter tone}} | {{Wikipedia|Quarter tone}} | ||
24edo is also known as '''quarter-tone tuning''', since it evenly divides the 12-tone equal tempered semitone in two. Quarter-tones are the most commonly used microtonal tuning due to its retention of the familiar 12 tones | 24edo is also known as '''quarter-tone tuning''', since it evenly divides the 12-tone equal tempered semitone in two. Quarter-tones are the most commonly used microtonal tuning due to its retention of the familiar 12 tones, since it is the smallest microtonal equal temperament that contains all the 12 notes, and also because of its use in theory and occasionally in practice in [[Arabic,_Turkish,_Persian|Arabic]] music. | ||
It is easy to jump into this tuning and make microtonal music right away using common 12 equal software and even instruments as illustrated in ''[[DIY Quartertone Composition with 12 equal tools]]''. | |||
== Theory == | == Theory == | ||
{{Odd harmonics in edo|edo=24}} | {{Odd harmonics in edo|edo=24}} | ||
The [[5-limit]] approximations in 24-tone equal temperament are the same as those in 12-tone equal temperament, therefore 24-tone equal temperament offers nothing new as far as approximating the 5-limit is concerned. The 7th harmonic-based intervals ([[7/4]], [[7/5]] and [[7/6]]) are almost as bad in 24-tET as in 12-tET. To achieve a satisfactory level of approximation while maintaining the 12 notes of 12-tET requires high-degree tunings like [[36edo|36et]], [[72edo|72et]], [[84edo|84et]] or [[156edo|156et]]. However, it should be noted that 24edo, like [[22edo]], ''does'' temper out the [[quartisma]], linking the otherwise sub-par 7-limit harmonies with those of the 11-limit | The [[5-limit]] approximations in 24-tone equal temperament are the same as those in 12-tone equal temperament, therefore 24-tone equal temperament offers nothing new as far as approximating the 5-limit is concerned. | ||
The 7th harmonic-based intervals ([[7/4]], [[7/5]] and [[7/6]]) are almost as bad in 24-tET as in 12-tET. To achieve a satisfactory level of approximation while maintaining the 12 notes of 12-tET requires high-degree tunings like [[36edo|36et]], [[72edo|72et]], [[84edo|84et]] or [[156edo|156et]]. However, it should be noted that 24edo, like [[22edo]], ''does'' temper out the [[quartisma]], linking the otherwise sub-par 7-limit harmonies with those of the 11-limit. | |||
Speaking of 11-limit representation in 24edo, the 11th harmonic, and most intervals derived from it, (11/10, 11/9, 11/8, 11/6, 12/11, 15/11, 16/11, 18/11, 20/11) are very well approximated in this EDO. The 24-tone interval of 550 cents is 1.3 cents flatter than 11:8 and is almost indistinguishable from it. In addition, the interval approximating 11:9 is 7 steps which is exactly half the perfect fifth. | |||
The tunings supplied by 72 cannot be used for all low-limit just intervals, but they can be used on the 17-limit [[k*N_subgroups|3*24 subgroup]] 2.3.125.35.11.325.17 [[just intonation subgroup]], making some of the excellent approximations of 72 available in 24edo. Chords based on this subgroup afford considerable scope for harmony, including in particular intervals and chords using only 2, 3, 11 and 17. Another approach would be to treat 24-EDO as a 2.3.11.17.19 subgroup temperament, on which it is quite accurate. | The tunings supplied by 72 cannot be used for all low-limit just intervals, but they can be used on the 17-limit [[k*N_subgroups|3*24 subgroup]] 2.3.125.35.11.325.17 [[just intonation subgroup]], making some of the excellent approximations of 72 available in 24edo. Chords based on this subgroup afford considerable scope for harmony, including in particular intervals and chords using only 2, 3, 11 and 17. Another approach would be to treat 24-EDO as a 2.3.11.17.19 subgroup temperament, on which it is quite accurate. | ||
| Line 21: | Line 27: | ||
== Notation == | == Notation == | ||
There are multiple ways of notating 24edo. | There are multiple ways of notating 24edo. While an arguably common form can be seen on [[Wikipedia: Quarter tone #Interval size in equal temperament|Wikipedia's page on quartertones]], there are other forms, and it is these other forms that will be considered here. | ||
For the full list, along with some chord progression information, see [[24edo interval names and harmonies|full article on 24 Edo intervals]], and also [[24edo Chord Names]] and [[Ups and Downs Notation#Chords and Chord Progressions]]. | |||
=== Ups and down notation === | === Ups and down notation === | ||
| Line 289: | Line 297: | ||
=== William Lynch's notation === | === William Lynch's notation === | ||
24 EDO breaks intervals into two sets of five cartegories. Infra - Minor - Neutral - Major - Ultra for seconds, thirds, sixths, and sevenths; and diminished - narrow - perfect - wide - augmented for fourths, fifths, unison, and octave. For other strange enharmonics, wide and narrow can be used in conjunction with augmented and diminished intervals such as 550 cents being called a narrow diminished fifth and 850 cents being called a wide augmented fifth. | 24 EDO breaks intervals into two sets of five cartegories. Infra - Minor - Neutral - Major - Ultra for seconds, thirds, sixths, and sevenths; and diminished - narrow - perfect - wide - augmented for fourths, fifths, unison, and octave. | ||
For other strange enharmonics, wide and narrow can be used in conjunction with augmented and diminished intervals such as 550 cents being called a narrow diminished fifth and 850 cents being called a wide augmented fifth. | |||
These are the intervals of 24 EDO that do not exist in 12 EDO: | These are the intervals of 24 EDO that do not exist in 12 EDO: | ||
| Line 407: | Line 417: | ||
The special alterations of the intervals and chords of 12 equal can be notated like this: | The special alterations of the intervals and chords of 12 equal can be notated like this: | ||
Supermajor or "'''Tendo'''" is a major interval raised a quarter tone | * Supermajor or "'''Tendo'''" is a major interval raised a quarter tone | ||
* Subminor or "'''Arto'''" is a minor interval lowered a quarter tone | |||
Subminor or "'''Arto'''" is a minor interval lowered a quarter tone | * Neutral are intervals that exist between the major and minor version of an interval | ||
* The prefix '''under''' indicates a perfect interval lowered by one quarter tone | |||
Neutral are intervals that exist between the major and minor version of an interval | * The prefix '''over''' indicates a perfect interval raised by a quarter tone | ||
* The Latin words "tendo" (meaning "expand") and "arto" (meaning "contract") can be used to replace the words "supermajor" and "subminor" in order to shorten the names of the intervals. | |||
The prefix '''under''' indicates a perfect interval lowered by one quarter tone | |||
The prefix '''over''' indicates a perfect interval raised by a quarter tone | |||
The Latin words "tendo" (meaning "expand") and "arto" (meaning "contract") can be used to replace the words "supermajor" and "subminor" in order to shorten the names of the intervals. | |||
==== Chord names ==== | ==== Chord names ==== | ||
| Line 425: | Line 430: | ||
They are: | They are: | ||
Super + perfect interval such as "perfect fifth" means to raise it by a quarter tone | * Super + perfect interval such as "perfect fifth" means to raise it by a quarter tone | ||
* Sub + perfect interval means to lower a quarter tone | |||
Sub + perfect interval means to lower a quarter tone | * Sharp is to raise by one half tone | ||
* Flat is to raise by a half tone | |||
Sharp is to raise by one half tone | * Neutral, arto and tendo refer to triads or tetrads | ||
* Neutral, arto, or tendo + interval name of 2nd, 3rd, 6th, or 7th is to alter respectively | |||
Flat is to raise by a half tone | |||
Neutral, arto and tendo refer to triads or tetrads | |||
Neutral, arto, or tendo + interval name of 2nd, 3rd, 6th, or 7th is to alter respectively | |||
Examples: | Examples: | ||
Neutral Super Eleventh or neut^11 = C neutral 7th chord with a super 11th thrown on top | * Neutral Super Eleventh or neut^11 = C neutral 7th chord with a super 11th thrown on top | ||
* Arto Sub Seventh Tendo Thirteenth or artsub7^13 = Arto tetrad with an arto seventh and a tendo thirteenth on top Minor Seventh Flat Five Arto Ninth Super Eleventh or m7b5^9^11 | |||
Arto Sub Seventh Tendo Thirteenth or artsub7^13 = Arto tetrad with an arto seventh and a tendo thirteenth on top Minor Seventh Flat Five Arto Ninth Super Eleventh or m7b5^9^11 | |||
== Quartertone accidentals == | == Quartertone accidentals == | ||
| Line 588: | Line 587: | ||
==Chord types== | ==Chord types== | ||
24edo features a rich variety of not only new chords, but also alterations that can be used with regular | 24edo features a rich variety of not only new chords, but also alterations that can be used with regular 12edo chords. For example, an approximation of the ninth, eleventh, and thirteenth harmonic can be added to a major triad to create a sort of super-extended chord structure of a major chord: 4:5:6:9:11:13. | ||
As for entirely new chords, the most obvious is the neutral or mid triad 0-7-14. However there are other options such as | As for entirely new chords, the most obvious is the neutral or mid triad 0-7-14. However there are other options such as: | ||
0-9-14 (Ultra Triad or upmajor triad) | * 0-9-14 (Ultra Triad or upmajor triad) | ||
* 0-5-14 (Infra Triad or downminor triad) | |||
These chords | These chords tend to lack the forcefulness to sound like resolved, tonal sonorities, but can be resolved of that issue by using tetrads in place of triads. For example, the neutral triad can have the neutral 7th added to it to make a full neutral tetrad: 0-7-14-21. However, another option is to replace the neutral third with an 11/8 to produce a sort of 11 limit neutral tetrad: 0-14-21-35 [[William Lynch]] considers this chord to be the most consonant tetrad in 24edo involving a neutral tonality. | ||
24 edo also is very good at 15 limit and does 13 quite well allowing barbodos 10:13:15 and barbodos minor triad 26:30:39 to be used as an entirely new harmonic system. | |||
More good chords in 24-tET: | More good chords in 24-tET: | ||
0-4-8-11-14 ("major" chord with a 9:8 and a 11:8 above the root) | * 0-4-8-11-14 ("major" chord with a 9:8 and a 11:8 above the root) | ||
* Its inversion, 0-3-6-10-14 ("minor") | |||
Its inversion, 0-3-6-10-14 ("minor") | * 0-5-10 (another kind of "neutral", splitting the fourth in two. The 0-5-10 can be extended into a pentatonic scale, 0-5-10-14-19-24 ([[godzilla]]), that is close to equi-pentatonic and also close to several Indonesian slêndros. In a similar way 0-7-14 extends to 0-4-7-11-14-18-21-24 ([[mohajira]]), a heptatonic scale close to several Arabic scales.) | ||
0-5-10 (another kind of "neutral", splitting the fourth in two. The 0-5-10 can be extended into a pentatonic scale, 0-5-10-14-19-24 ([[godzilla]]), that is close to equi-pentatonic and also close to several Indonesian slêndros. In a similar way 0-7-14 extends to 0-4-7-11-14-18-21-24 ([[mohajira]]), a heptatonic scale close to several Arabic scales.) | |||
William Lynch considers these as some possible good tetrads: | William Lynch considers these as some possible good tetrads: | ||
| Line 863: | Line 861: | ||
== Counterpoint == | == Counterpoint == | ||
24edo is the first edo to have both a [[sqrt(25/24)]] distinct from [[25/24]] and a correct [[5-odd-limit]]. | 24edo is the first edo to have both a [[sqrt(25/24)]] distinct from [[25/24]] and a correct [[5-odd-limit]]. It is thus the first edo which allows to lead the two voices of a major third to a minor third by [[strict contrary motion]]. And vice versa. | ||
It is thus the first edo which allows to lead the two voices of a major third to a minor third by [[strict contrary motion]]. And vice versa. | |||
Furthermore, in the same fashion, every sequence of intervals available in 12edo are reachable by equal contrary motion in 24edo. | Furthermore, in the same fashion, every sequence of intervals available in 12edo are reachable by equal contrary motion in 24edo. | ||
| Line 887: | Line 883: | ||
==Music== | ==Music== | ||
[https:// | * <span style="">[http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Mohajeri/Microhex3.mp3 Microhex3]</span> <span style="">[http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Mohajeri/Microhex4.mp3 Microhex4]</span> and <span style="">[http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Mohajeri/Microhex5.mp3 Microhex5]</span> by [http://www.96edo.com/About_me.html Shaahin Mohajeri] | ||
* <span style="">[http://micro.soonlabel.com/24et/quarterpicnic.mp3 Quarterpicnic]</span> by [[Chris Vaisvil]] | |||
* [http://micro.soonlabel.com/gene_ward_smith/Others/BeDell/Quarter%20Tone%20Prelude%20for%20two%20Harps.mp3 Quarter Tone Prelude For Two Harps] by [https://soundcloud.com/cerbeus-1/quarter-tone-prelude-for-two Nathan BeDell] | |||
* <span style="">[http://micro.soonlabel.com/24et/daily20111021-fretless-1.mp3 Fretless Chrome 1]</span> and <span style="">[http://micro.soonlabel.com/24et/daily20111021-fretless-2.mp3 Fretless Chrome 2]</span> by [http://chrisvaisvil.com/?p=1477 Chris Vaisvil] | |||
* [http://micro.soonlabel.com/gene_ward_smith/Others/Freivald/Lament.mp3 Lament] by [https://soundcloud.com/jdfreivald/lament Jake Freivald]. In the [[freivaldneutral24]] scale. | |||
* [https://soundcloud.com/jdfreivald/mo-happy-happy Mo - Happy - Happy] [http://micro.soonlabel.com/gene_ward_smith/Others/Freivald/mo-happy-happy.mp3 play] by Jake Freivald in Neutral[7] (2.3.11 mohajira), 24et tuning | |||
* [https://www.youtube.com/watch?v=q1Lp8AtKK9o Autumn Winds], [https://www.youtube.com/watch?v=Igxe3DwbFJ4&feature=c4-overview&list=UUvq5bg-LvOS6adpB5efPTyQ Easter Time at Nine], [https://www.youtube.com/watch?v=z_3uhA9Cq08&list=UUvq5bg-LvOS6adpB5efPTyQ Waters of Persia] by William Lynch in mohajira, 24et tuning. | |||
* [https://soundcloud.com/mason-l-green/serena Serena], by Mason Green (intro and coda in 24edo, the rest is in 12edo) | |||
* [https://www.youtube.com/watch?v=yzvXEMYgHCY Autumn Girl], by Mason Green | |||
* "Prométhée enchaîné" by [[wikipedia:Fromental_Halévy|Fromental Halévy]] (considered the first mainstream western orchestral composition to use quarter tones.) | |||
* "3 Hommages" by [[wikipedia:Georg_Friedrich_Haas|Georg Friedrich Haas]] | |||
* "Folly of a Drunk" by Dawson Berry ([[:File:Folly of a Drunk.mp3|mp3]]) ([[:File:Folly of a Drunk (Musescore 3).pdf|score]]) | |||
* [[wikipedia:List_of_quarter_tone_pieces|List of quartertone pieces on Wikipedia]] | |||
== Further reading == | == Further reading == | ||
Revision as of 09:19, 20 April 2023
| ← 23edo | 24edo | 25edo → |
24edo is also known as quarter-tone tuning, since it evenly divides the 12-tone equal tempered semitone in two. Quarter-tones are the most commonly used microtonal tuning due to its retention of the familiar 12 tones, since it is the smallest microtonal equal temperament that contains all the 12 notes, and also because of its use in theory and occasionally in practice in Arabic music.
It is easy to jump into this tuning and make microtonal music right away using common 12 equal software and even instruments as illustrated in DIY Quartertone Composition with 12 equal tools.
Theory
| Odd harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | absolute (¢) | -2.0 | +13.7 | -18.8 | -3.9 | -1.3 | +9.5 | +11.7 | -5.0 | +2.5 | -20.8 | +21.7 | -22.6 | -5.9 | +20.4 | +5.0 |
| relative (%) | -4 | +27 | -38 | -8 | -3 | +19 | +23 | -10 | +5 | -42 | +43 | -45 | -12 | +41 | +10 | |
| Steps (reduced) | 38 (14) | 56 (8) | 67 (19) | 76 (4) | 83 (11) | 89 (17) | 94 (22) | 98 (2) | 102 (6) | 105 (9) | 109 (13) | 111 (15) | 114 (18) | 117 (21) | 119 (23) | |
The 5-limit approximations in 24-tone equal temperament are the same as those in 12-tone equal temperament, therefore 24-tone equal temperament offers nothing new as far as approximating the 5-limit is concerned.
The 7th harmonic-based intervals (7/4, 7/5 and 7/6) are almost as bad in 24-tET as in 12-tET. To achieve a satisfactory level of approximation while maintaining the 12 notes of 12-tET requires high-degree tunings like 36et, 72et, 84et or 156et. However, it should be noted that 24edo, like 22edo, does temper out the quartisma, linking the otherwise sub-par 7-limit harmonies with those of the 11-limit.
Speaking of 11-limit representation in 24edo, the 11th harmonic, and most intervals derived from it, (11/10, 11/9, 11/8, 11/6, 12/11, 15/11, 16/11, 18/11, 20/11) are very well approximated in this EDO. The 24-tone interval of 550 cents is 1.3 cents flatter than 11:8 and is almost indistinguishable from it. In addition, the interval approximating 11:9 is 7 steps which is exactly half the perfect fifth.
The tunings supplied by 72 cannot be used for all low-limit just intervals, but they can be used on the 17-limit 3*24 subgroup 2.3.125.35.11.325.17 just intonation subgroup, making some of the excellent approximations of 72 available in 24edo. Chords based on this subgroup afford considerable scope for harmony, including in particular intervals and chords using only 2, 3, 11 and 17. Another approach would be to treat 24-EDO as a 2.3.11.17.19 subgroup temperament, on which it is quite accurate.
24edo is the 6th highly composite EDO.
Notation
There are multiple ways of notating 24edo. While an arguably common form can be seen on Wikipedia's page on quartertones, there are other forms, and it is these other forms that will be considered here.
For the full list, along with some chord progression information, see full article on 24 Edo intervals, and also 24edo Chord Names and Ups and Downs Notation#Chords and Chord Progressions.
Ups and down notation
| Degree | Cents | Approximate Ratios[1] | ups and downs notation | Solfege | ||
|---|---|---|---|---|---|---|
| 0 | 0 | 1/1 | P1 | unison | C | Do |
| 1 | 50 | 33/32, 34/33 | ^P1, vm2 | up-unison, downminor 2nd | ^C, vDb | Da/Ru |
| 2 | 100 | 17/16, 18/17 | A1, m2 | aug unison, minor 2nd | C#, Db | Ro |
| 3 | 150 | 12/11 | ~2 | mid 2nd | vD | Ra |
| 4 | 200 | 9/8 | M2 | major 2nd | D | Re |
| 5 | 250 | 22/19 | ^M2, vm3 | upmajor 2nd, downminor 3rd | ^D, vEb | Ri/Mu |
| 6 | 300 | 19/16 | m3 | minor 3rd | Eb | Mo |
| 7 | 350 | 11/9, 27/22 | ~3 | mid 3rd | vE | Ma |
| 8 | 400 | 24/19 | M3 | major 3rd | E | Me |
| 9 | 450 | 22/17 | ^M3, v4 | upmajor 3rd, down-4th | ^E, vF | Mi/Fu |
| 10 | 500 | 4/3 | P4 | fourth | F | Fo |
| 11 | 550 | 11/8 | ^4, ~4 | up-4th, mid-4th | ^F | Fa/Su |
| 12 | 600 | 17/12 | A4, d5 | aug 4th, dim 5th | F#, Gb | Fe/So |
| 13 | 650 | 16/11 | v5, ~5 | down-5th, mid-5th | vG | Fi/Sa |
| 14 | 700 | 3/2 | P5 | fifth | G | Se |
| 15 | 750 | 17/11 | ^5, vm6 | up-fifth, downminor 6th | ^G, vAb | Si/Lu |
| 16 | 800 | 19/12 | m6 | minor 6th | Ab | Lo |
| 17 | 850 | 18/11, 44/27 | ~6 | mid 6th | vA | La |
| 18 | 900 | 32/19 | M6 | major 6th | A | Le |
| 19 | 950 | 19/11 | ^M6, vm7 | upmajor 6th, downminor 7th | ^A, vBb | Li/Tu |
| 20 | 1000 | 16/9 | m7 | minor 7th | Bb | To |
| 21 | 1050 | 11/6 | ~7 | mid 7th | vB | Ta |
| 22 | 1100 | 17/9, 32/17 | M7 | major 7th | B | Te |
| 23 | 1150 | 33/17, 64/33 | ^M7, vP8 | upmajor 7th, down-8ve | ^B, vC | Ti/Du |
| 24 | 1200 | 2/1 | P8 | perfect 8ve | C | Do |
In many other edos, 5/4 is downmajor and 11/9 is mid. To agree with this, the term mid is generally preferred over down or downmajor.
Combining ups and downs notation with color notation, qualities can be loosely associated with colors:
| quality | color name | monzo format | examples |
|---|---|---|---|
| downminor | zo | (a, b, 0, 1) | 7/6, 7/4 |
| minor | fourthward wa | (a, b), b < -1 | 32/27, 16/9 |
| gu | (a, b, -1) | 6/5, 9/5 | |
| mid | ilo | (a, b, 0, 0, 1) | 11/9, 11/6 |
| lu | (a, b, 0, 0, -1) | 12/11, 18/11 | |
| major | yo | (a, b, 1) | 5/4, 5/3 |
| fifthward wa | (a, b), b > 1 | 9/8, 27/16 | |
| upmajor | ru | (a, b, 0, -1) | 9/7, 12/7 |
Ups and downs notation can be used to name chords. See 24edo Chord Names and Ups and Downs Notation#Chords and Chord Progressions.
William Lynch's notation
24 EDO breaks intervals into two sets of five cartegories. Infra - Minor - Neutral - Major - Ultra for seconds, thirds, sixths, and sevenths; and diminished - narrow - perfect - wide - augmented for fourths, fifths, unison, and octave.
For other strange enharmonics, wide and narrow can be used in conjunction with augmented and diminished intervals such as 550 cents being called a narrow diminished fifth and 850 cents being called a wide augmented fifth.
These are the intervals of 24 EDO that do not exist in 12 EDO:
| The twelve new intervals in 24edo | some nearby JI intervals | |||||
|---|---|---|---|---|---|---|
| cents | pions | 7mus (hex) | common names | frequency ratio | cents | common name |
| 50 | 53 | 64 (4016) | quartertone infra second, wide unison |
36/35 35/34 34/33 33/32 |
48.770 50.184 51.682 53.273 |
large septimal quarter-tone (Archytas) large 17-limit quartertone small 17-limit quartertone 33rd harmonic |
| 150 | 159 | 192 (C016) | neutral second | 12/11 | 150.637 | large undecimal neutral second |
| 250 | 265 | 320 (14016) | ultra second infra third |
144/125 15/13 52/45 |
244.969 247.741 250.304 |
diminished third (6/5 x 24/25) .. .. |
| 350 | 383 | 448 (1C016) | neutral third | 11/9 27/22 16/13 |
347.408 354.547 359.472 |
undecimal neutral third .. tridecimal neutral third |
| 450 | 477 | 576 (24016) | minor fourth, ultra third, narrow fourth | 22/17 35/27 13/10 |
446.363 449.275 454.214 |
17-limit supermajor third .. tridecimal subfourth |
| 550 | 583 | 704 (2C016) | wide fourth | 11/8 | 551.318 | undecimal superfourth, harmonic 11th |
| 650 | 689 | 832 (34016) | narrow fifth | 16/11 | 648.682 | undecimal subfifth, 11th subharmonic |
| 750 | 795 | 960 (3C016) | wide fifth, infra sixth | 20/13 54/35 17/11 |
745.786 750.725 753.637 |
tridecimal superfifth .. 17-limit subminor sixth |
| 850 | 901 | 1088 (34016) | neutral sixth | 13/8 44/27 18/11 |
840.528 845.453 852.592 |
overtone sixth, 13th harmonic .. undecimal neutral sixth |
| 950 | 1007 | 1216 (4C016) | ultra sixth , infra seventh | 45/26 26/15 125/72 |
949.696 952.259 955.031 |
.. .. .. |
| 1050 | 1113 | 1344 (54016) | neutral seventh | 11/6 | 1049.363 | undecimal neutral seventh |
| 1150 | 1219 | 1472 (5C016) | ultra seventh, narrow octave | 31/16 33/17 35/18 |
1145.036 1148.318 1151.230 |
31st harmonic .. .. |
Interval alterations
The special alterations of the intervals and chords of 12 equal can be notated like this:
- Supermajor or "Tendo" is a major interval raised a quarter tone
- Subminor or "Arto" is a minor interval lowered a quarter tone
- Neutral are intervals that exist between the major and minor version of an interval
- The prefix under indicates a perfect interval lowered by one quarter tone
- The prefix over indicates a perfect interval raised by a quarter tone
- The Latin words "tendo" (meaning "expand") and "arto" (meaning "contract") can be used to replace the words "supermajor" and "subminor" in order to shorten the names of the intervals.
Chord names
Naming chords in 24edo can be achieved by adding a few things to the already existing set of terms that are used to name 12edo chords.
They are:
- Super + perfect interval such as "perfect fifth" means to raise it by a quarter tone
- Sub + perfect interval means to lower a quarter tone
- Sharp is to raise by one half tone
- Flat is to raise by a half tone
- Neutral, arto and tendo refer to triads or tetrads
- Neutral, arto, or tendo + interval name of 2nd, 3rd, 6th, or 7th is to alter respectively
Examples:
- Neutral Super Eleventh or neut^11 = C neutral 7th chord with a super 11th thrown on top
- Arto Sub Seventh Tendo Thirteenth or artsub7^13 = Arto tetrad with an arto seventh and a tendo thirteenth on top Minor Seventh Flat Five Arto Ninth Super Eleventh or m7b5^9^11
Quartertone accidentals
Besides ups and downs, there are various systems for notating quarter tones. Here are some of them, along with their pros and cons.
Mainstream quartertone notation
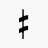
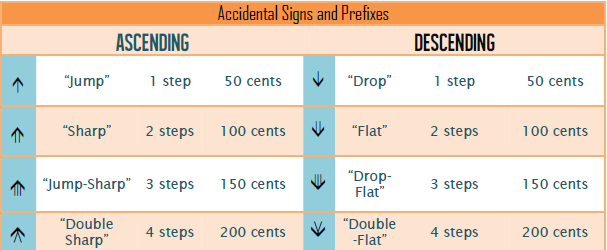
or ^ = quarter-tone sharp or "Jump" or "up"

or #^ or ^# = three-quarter-tone sharp or "Jump-Sharp" or "upsharp"
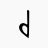
or v = quarter-tone flat or "Drop" or "down"

or bv or vb = three-quarter-tone sharp or "Drop-Flat" or "downflat"
Pros: Familiar, fairly easy to learn
Cons: Clutters a score easily, can get confusing when sight read at faster paces
Alternate quartertone accidentals
External image: http://faculty.mansfield.edu/jmurphy/oldsite/quartertonesharp.gif
- WARNING: MediaWiki doesn't have very good support for external images.
- Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.
= quarter-tone sharp or Jump
††† (the horizontal line should connect all three vertical lines) = three quarter-tones sharp or Jump-Sharp
External image: http://www.dolmetsch.com/onequarterflat.gif
- WARNING: MediaWiki doesn't have very good support for external images.
- Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.
= quarter-tone flat or Drop
External image: http://upload.wikimedia.org/wikipedia/commons/thumb/1/1b/Arabic_music_notation_half_flat.svg/9px-Arabic_music_notation_half_flat.svg.png
- WARNING: MediaWiki doesn't have very good support for external images.
- Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.
= three quarter-tones flat or drop-flat
For example, the scale 0-5-10-15-20 is written as C-D
External image: http://faculty.mansfield.edu/jmurphy/oldsite/quartertonesharp.gif
- WARNING: MediaWiki doesn't have very good support for external images.
- Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.
(or E
External image: http://upload.wikimedia.org/wikipedia/commons/thumb/1/1b/Arabic_music_notation_half_flat.svg/9px-Arabic_music_notation_half_flat.svg.png
- WARNING: MediaWiki doesn't have very good support for external images.
- Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.
) F G
External image: http://faculty.mansfield.edu/jmurphy/oldsite/quartertonesharp.gif
- WARNING: MediaWiki doesn't have very good support for external images.
- Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.
(or A
External image: http://upload.wikimedia.org/wikipedia/commons/thumb/1/1b/Arabic_music_notation_half_flat.svg/9px-Arabic_music_notation_half_flat.svg.png
- WARNING: MediaWiki doesn't have very good support for external images.
- Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.
) Bb.
Pros: Very easy to distinguish accidentals from one another
Cons: Not practical, tends to clutter a score
Persian accidentals
| Koron (en | fa) = quarter-tone flat |
| Sori (fa) = quarter-tone sharp |
Pros: Easy to read
Cons: Hard to write on a computer, doesn't fit with standard notation well
Sagittal notation
Sagittal notation works extremely well for 24edo notation as well as other systems.
It is easy on the eyes, easy to recognize the various symbols and keeps a score looking tidy and neat.
A possibility for the best approach would be to not use traditional sharps and flats altogether and replace them
with Sagittal signs for sharp and flat.
Pros: Easy to read, and less likely to clutter the score
Cons: Not as familiar as traditional notation, and thus not immediately accessible to many traditional musicians who are just starting out with microtonality
We also have, from the appendix to The Sagittal Songbook by Jacob A. Barton, a diagram of how to notate 24-EDO in the Revo flavor of Sagittal:
Chord types
24edo features a rich variety of not only new chords, but also alterations that can be used with regular 12edo chords. For example, an approximation of the ninth, eleventh, and thirteenth harmonic can be added to a major triad to create a sort of super-extended chord structure of a major chord: 4:5:6:9:11:13.
As for entirely new chords, the most obvious is the neutral or mid triad 0-7-14. However there are other options such as:
- 0-9-14 (Ultra Triad or upmajor triad)
- 0-5-14 (Infra Triad or downminor triad)
These chords tend to lack the forcefulness to sound like resolved, tonal sonorities, but can be resolved of that issue by using tetrads in place of triads. For example, the neutral triad can have the neutral 7th added to it to make a full neutral tetrad: 0-7-14-21. However, another option is to replace the neutral third with an 11/8 to produce a sort of 11 limit neutral tetrad: 0-14-21-35 William Lynch considers this chord to be the most consonant tetrad in 24edo involving a neutral tonality.
24 edo also is very good at 15 limit and does 13 quite well allowing barbodos 10:13:15 and barbodos minor triad 26:30:39 to be used as an entirely new harmonic system.
More good chords in 24-tET:
- 0-4-8-11-14 ("major" chord with a 9:8 and a 11:8 above the root)
- Its inversion, 0-3-6-10-14 ("minor")
- 0-5-10 (another kind of "neutral", splitting the fourth in two. The 0-5-10 can be extended into a pentatonic scale, 0-5-10-14-19-24 (godzilla), that is close to equi-pentatonic and also close to several Indonesian slêndros. In a similar way 0-7-14 extends to 0-4-7-11-14-18-21-24 (mohajira), a heptatonic scale close to several Arabic scales.)
William Lynch considers these as some possible good tetrads:
| Chord name | Degrees of 24edo | Chord spelling | Audio example |
|---|---|---|---|
| neutral | 0 7 14 21 | 1 v3 5 v7 | |
| arto | 0 5 14 20 | 1 vb3 5 b7 | |
| tendo | 0 9 14 19 | 1 ^3 5 vb7 | ... |
The tendo chord can also be spelled 1 ^3 5 ^6. Due to convenience, the names Arto and tendo have been changed to Ultra and Infra.
Commas
24edo tempers out the following commas. This assumes val ⟨24 38 56 67 83 89].
| Prime Limit |
Ratio[1] | Monzo | Cents | Color name | Name(s) |
|---|---|---|---|---|---|
| 3 | (12 digits) | [-19 12⟩ | 23.46 | Lalawa | Pythagorean comma |
| 5 | 648/625 | [3 4 -4⟩ | 62.57 | Quadgu | Major diesis, diminished domma |
| 5 | 128/125 | [7 0 -3⟩ | 41.06 | Trigu | Diesis, augmented comma |
| 5 | 81/80 | [-4 4 -1⟩ | 21.51 | Gu | Syntonic comma, Didymus comma, meantone comma |
| 5 | 2048/2025 | [11 -4 -2⟩ | 19.55 | Sagugu | Diaschisma |
| 5 | (16 digits) | [26 -12 -3⟩ | 17.60 | Sasa-trigu | Misty comma |
| 5 | 32805/32768 | [-15 8 1⟩ | 1.95 | Layo | Schisma |
| 5 | (98 digits) | [161 -84 -12⟩ | 0.02 | Sepbisa-quadbigu | Atom |
| 7 | 49/48 | [-4 -1 0 2⟩ | 35.70 | Zozo | Slendro diesis |
| 7 | 245/243 | [0 -5 1 2⟩ | 14.19 | Zozoyo | Sensamagic |
| 7 | 19683/19600 | [-4 9 -2 -2⟩ | 7.32 | Labirugu | Cataharry |
| 7 | 6144/6125 | [11 1 -3 -2⟩ | 5.36 | Sarurutrigu | Porwell |
| 11 | 121/120 | [-3 -1 -1 0 2⟩ | 14.37 | Lologu | Biyatisma |
| 11 | 176/175 | [4 0 -2 -1 1⟩ | 9.86 | Lorugugu | Valinorsma |
| 11 | 896/891 | [7 -4 0 1 -1⟩ | 9.69 | Saluzo | Pentacircle |
| 11 | 243/242 | [-1 5 0 0 -2⟩ | 7.14 | Lulu | Rastma |
| 11 | 385/384 | [-7 -1 1 1 1⟩ | 4.50 | Lozoyo | Keenanisma |
| 11 | 9801/9800 | [-3 4 -2 -2 2⟩ | 0.18 | Bilorugu | Kalisma, Gauss' comma |
| 13 | 91/90 | [-1 -2 -1 1 0 1⟩ | 19.13 | Thozogu | Superleap |
| 13 | 676/675 | [2 -3 -2 0 0 2⟩ | 2.56 | Bithogu | Island comma, parizeksma |
- ↑ Ratios longer than 10 digits are presented by placeholders with informative hints
Rank-2 temperaments
Important MOSes include:
- semaphore 4L1s 55455 (generator: 5\24)
- semaphore 5L4s 414144141 (generator: 5\24)
- mohajira 3L4s 3434343 (generator: 7\24)
- mohajira 7L3s 3313313313 (generator: 7\24)
| Periods per octave | Generator | Name |
|---|---|---|
| 1 | 1\24 | |
| 1 | 5\24 | Semaphore/godzilla / Bridgetown |
| 1 | 7\24 | Mohajira (or maqamic with 24d val) |
| 1 | 11\24 | Barton |
| 2 | 1\24 | Shrutar |
| 2 | 5\24 | Sruti, Anguirus, Decimal |
| 3 | 1\24 | Semiaug |
| 3 | 3\24 | Triforce |
| 4 | 1\24 | Hemidim |
| 6 | 1\24 | Hemisemiaug |
| 8 | 1\24 | Semidim |
| 12 | 1\24 | Catler |
Scales / modes
See 24edo modes.
Tetrachords
See 24edo tetrachords.
Counterpoint
24edo is the first edo to have both a sqrt(25/24) distinct from 25/24 and a correct 5-odd-limit. It is thus the first edo which allows to lead the two voices of a major third to a minor third by strict contrary motion. And vice versa.
Furthermore, in the same fashion, every sequence of intervals available in 12edo are reachable by equal contrary motion in 24edo.
 |
Instruments
The ever-arising question in microtonal music, how to play it on instruments designed for 12edo, has a relatively simple answer in the case of 24edo: use two standard instruments tuned a quartertone apart. This "12 note octave scales" approach is used in a wide part of the existing literature - see below.
External image: http://www.swordguitars.com/Sword_quartertone_stratsm.jpg
- WARNING: MediaWiki doesn't have very good support for external images.
- Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.
24-tone "1/4-tone" Guitar by Ron Sword / Sword guitars
Hidekazu Wakabayashi tuned a piano and harp to where the normal sharps and flats are tuned 50 cents higher in which he called Iceface tuning.
Music
- Microhex3 Microhex4 and Microhex5 by Shaahin Mohajeri
- Quarterpicnic by Chris Vaisvil
- Quarter Tone Prelude For Two Harps by Nathan BeDell
- Fretless Chrome 1 and Fretless Chrome 2 by Chris Vaisvil
- Lament by Jake Freivald. In the freivaldneutral24 scale.
- Mo - Happy - Happy play by Jake Freivald in Neutral[7] (2.3.11 mohajira), 24et tuning
- Autumn Winds, Easter Time at Nine, Waters of Persia by William Lynch in mohajira, 24et tuning.
- Serena, by Mason Green (intro and coda in 24edo, the rest is in 12edo)
- Autumn Girl, by Mason Green
- "Prométhée enchaîné" by Fromental Halévy (considered the first mainstream western orchestral composition to use quarter tones.)
- "3 Hommages" by Georg Friedrich Haas
- "Folly of a Drunk" by Dawson Berry (mp3) (score)
- List of quartertone pieces on Wikipedia
Further reading
- Ellis, Don. Quarter Tones: A Text with Musical Examples, Exercises and Etudes. 1975.
- Sword, Ron. Icosikaitetraphonic Scales for Guitar: Theory and Scales for Twenty-four Equal Divisions of the Octave. 2009. (Features a practical approach to understanding the tuning, and over 550 scale examples on nine-string finger board charts, which allows for both symmetrical tuning visualization and standard guitar tuning- helpful for bassists and large range guitarists as well. Includes MOS, DE, and *all* the scales/modes from the list above.)