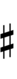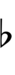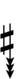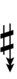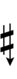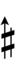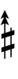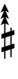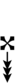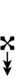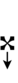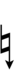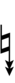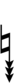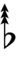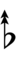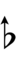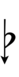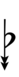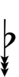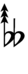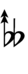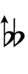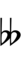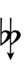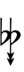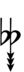56edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
BudjarnLambeth (talk | contribs)
autopatrolled
18,200 edits
m →Theory: (''See regular temperament for more about what all this means and how to use it.'')
Tag: Reverted
→Music: Add Bryan Deister's ''Waltz in 56edo'' (2025)
 
(11 intermediate revisions by 6 users not shown)
Line 5: Line 5:
56edo shares its near perfect quality of classical major third with [[28edo]], which it doubles, while also adding a superpythagorean 5th that is a convergent towards the [[Metallic harmonic series|bronze metallic mean]], following [[17edo]] and preceding [[185edo]]. Because it contains 28edo's major third and also has a step size very close to the syntonic comma, 56edo contains very accurate approximations of both the classic major third [[5/4]] and the Pythagorean major third [[81/64]]. Unfortunately, this "Pythagorean major third" is not the major third as is stacked by fifths in 56edo.  
56edo shares its near perfect quality of classical major third with [[28edo]], which it doubles, while also adding a superpythagorean 5th that is a convergent towards the [[Metallic harmonic series|bronze metallic mean]], following [[17edo]] and preceding [[185edo]]. Because it contains 28edo's major third and also has a step size very close to the syntonic comma, 56edo contains very accurate approximations of both the classic major third [[5/4]] and the Pythagorean major third [[81/64]]. Unfortunately, this "Pythagorean major third" is not the major third as is stacked by fifths in 56edo.  


56edo can be used to tune [[hemithirds]], [[superkleismic]], [[sycamore]] and [[keen]] temperaments, and using {{val| 56 89 130 158 }} (56d) as the equal temperament val, for [[pajara]]. It provides the [[optimal patent val]] for 7-, 11- and 13-limit [[sycamore]], and the 11-limit 56d val is close to the [[POTE tuning]] for 11-limit pajara. (''See [[regular temperament]] for more about what all this means and how to use it.'')
One step of 56edo is the closest direct approximation to the syntonic comma, [[81/80]], with the number of directly approximated syntonic commas per octave being 55.7976. (However, note that by [[patent val]] mapping, 56edo actually maps the syntonic comma inconsistently, to two steps.) [[Barium]] temperament realizes this proximity through regular temperament theory, and is supported by notable edos like [[224edo]], [[1848edo]], and [[2520edo]], which is a highly composite edo.
 
56edo can be used to tune [[hemithirds]], [[superkleismic]], [[sycamore]] and [[keen]] temperaments, and using {{val| 56 89 130 158 }} (56d) as the equal temperament val, for [[pajara]]. It provides the [[optimal patent val]] for 7-, 11- and 13-limit [[sycamore]], and the 11-limit 56d val is close to the [[POTE tuning]] for 11-limit pajara.  


=== Prime harmonics ===
=== Prime harmonics ===
Line 12: Line 14:
=== Subsets and supersets ===
=== Subsets and supersets ===
Since 56 factors into {{nowrap|2<sup>3</sup> &times; 7}}, 56edo has subset edos {{EDOs| 2, 4, 7, 8, 14, 28 }}.
Since 56 factors into {{nowrap|2<sup>3</sup> &times; 7}}, 56edo has subset edos {{EDOs| 2, 4, 7, 8, 14, 28 }}.
One step of 56edo is the closest direct approximation to the syntonic comma, [[81/80]], with the unrounded value being 55.7976. Barium temperament realizes this proximity through regular temperament theory, and is supported by notable edos like [[224edo]], [[1848edo]], and [[2520edo]], which is a highly composite edo.


== Intervals ==
== Intervals ==
{| class="wikitable center-all right-2 left-3"
{| class="wikitable center-all right-2 left-3"
|-
|-
! &#35;
! #
! Cents
! Cents
! Approximate ratios*
! Approximate ratios*
Line 24: Line 24:
|-
|-
| 0
| 0
| 0.000
| 0.0
| [[1/1]]
| [[1/1]]
| {{UDnote|step=0}}
| {{UDnote|step=0}}
|-
|-
| 1
| 1
| 21.429
| 21.4
| ''[[49/48]]'', [[64/63]]
| ''[[49/48]]'', [[55/54]], [[56/55]], [[64/63]]
| {{UDnote|step=1}}
| {{UDnote|step=1}}
|-
|-
| 2
| 2
| 42.857
| 42.9
| ''[[28/27]]'', [[50/49]], ''[[81/80]]''
| ''[[28/27]]'', [[40/39]], [[45/44]], [[50/49]], ''[[81/80]]''
| {{UDnote|step=2}}
| {{UDnote|step=2}}
|-
|-
| 3
| 3
| 64.286
| 64.3
| [[25/24]], ''[[36/35]]'', ''[[33/32]]''
| [[25/24]], ''[[36/35]]'', ''[[33/32]]''
| {{UDnote|step=3}}
| {{UDnote|step=3}}
|-
|-
| 4
| 4
| 85.714
| 85.7
| [[21/20]], [[22/21]]
| [[19/18]], [[20/19]], [[21/20]], [[22/21]]
| {{UDnote|step=4}}
| {{UDnote|step=4}}
|-
|-
| 5
| 5
| 107.143
| 107.1
| [[16/15]]
| [[16/15]], [[17/16]], [[18/17]]
| {{UDnote|step=5}}
| {{UDnote|step=5}}
|-
|-
| 6
| 6
| 128.571
| 128.6
| [[15/14]], [[13/12]], [[14/13]]
| [[15/14]], [[13/12]], [[14/13]]
| {{UDnote|step=6}}
| {{UDnote|step=6}}
|-
|-
| 7
| 7
| 150.000
| 150.0
| [[12/11]]
| [[12/11]]
| {{UDnote|step=7}}
| {{UDnote|step=7}}
|-
|-
| 8
| 8
| 171.429
| 171.4
| ''[[10/9]]'', [[11/10]]
| ''[[10/9]]'', [[11/10]], [[21/19]]
| {{UDnote|step=8}}
| {{UDnote|step=8}}
|-
|-
| 9
| 9
| 192.857
| 192.9
| [[28/25]]
| [[19/17]], [[28/25]]
| {{UDnote|step=9}}
| {{UDnote|step=9}}
|-
|-
| 10
| 10
| 214.286
| 214.3
| [[9/8]]
| [[9/8]], [[17/15]]
| {{UDnote|step=10}}
| {{UDnote|step=10}}
|-
|-
| 11
| 11
| 235.714
| 235.7
| [[8/7]]
| [[8/7]]
| {{UDnote|step=11}}
| {{UDnote|step=11}}
|-
|-
| 12
| 12
| 257.143
| 257.1
| [[7/6]], [[15/13]]
| [[7/6]]
| {{UDnote|step=12}}
| {{UDnote|step=12}}
|-
|-
| 13
| 13
| 278.571
| 278.6
| [[75/64]], [[13/11]]
| [[13/11]], [[20/17]]
| {{UDnote|step=13}}
| {{UDnote|step=13}}
|-
|-
| 14
| 14
| 300.000
| 300.0
| [[25/21]]
| [[19/16]], [[25/21]]
| {{UDnote|step=14}}
| {{UDnote|step=14}}
|-
|-
| 15
| 15
| 321.429
| 321.4
| [[6/5]]
| [[6/5]]
| {{UDnote|step=15}}
| {{UDnote|step=15}}
|-
|-
| 16
| 16
| 342.857
| 342.9
| [[11/9]], [[39/32]]
| [[11/9]], [[17/14]]
| {{UDnote|step=16}}
| {{UDnote|step=16}}
|-
|-
| 17
| 17
| 364.286
| 364.3
| [[27/22]], [[16/13]], [[26/21]]
| [[16/13]], [[21/17]], [[26/21]]
| {{UDnote|step=17}}
| {{UDnote|step=17}}
|-
|-
| 18
| 18
| 385.714
| 385.7
| [[5/4]]
| [[5/4]]
| {{UDnote|step=18}}
| {{UDnote|step=18}}
|-
|-
| 19
| 19
| 407.143
| 407.1
| [[14/11]]
| [[14/11]], [[19/12]], [[24/19]]
| {{UDnote|step=19}}
| {{UDnote|step=19}}
|-
|-
| 20
| 20
| 428.571
| 428.6
| [[32/25]], [[33/26]]
| [[32/25]], [[33/26]]
| {{UDnote|step=20}}
| {{UDnote|step=20}}
|-
|-
| 21
| 21
| 450.000
| 450.0
| ''[[9/7]]'', [[13/10]]
| ''[[9/7]]'', [[13/10]]
| {{UDnote|step=21}}
| {{UDnote|step=21}}
|-
|-
| 22
| 22
| 471.429
| 471.4
| [[21/16]]
| [[17/13]], [[21/16]]
| {{UDnote|step=22}}
| {{UDnote|step=22}}
|-
|-
| 23
| 23
| 492.857
| 492.9
| [[4/3]]
| [[4/3]]
| {{UDnote|step=23}}
| {{UDnote|step=23}}
|-
|-
| 24
| 24
| 514.286
| 514.3
| [[35/26]]
| [[35/26]]
| {{UDnote|step=24}}
| {{UDnote|step=24}}
|-
|-
| 25
| 25
| 535.714
| 535.7
| ''[[27/20]]'', [[15/11]]
| [[15/11]], [[19/14]], [[26/19]], ''[[27/20]]''
| {{UDnote|step=25}}
| {{UDnote|step=25}}
|-
|-
| 26
| 26
| 557.143
| 557.1
| [[11/8]]
| [[11/8]]
| {{UDnote|step=26}}
| {{UDnote|step=26}}
|-
|-
| 27
| 27
| 578.571
| 578.6
| [[7/5]]
| [[7/5]]
| {{UDnote|step=27}}
| {{UDnote|step=27}}
|-
|-
| 28
| 28
| 600.000
| 600.0
| [[45/32]], [[64/45]]
| [[17/12]], [[24/17]]
| {{UDnote|step=28}}
| {{UDnote|step=28}}
|-
|-
Line 173: Line 173:
| …
| …
|}
|}
<nowiki />* The following table assumes the [[patent val]] {{val| 56 89 130 157 194 207 }}; other approaches are possible. Inconsistent intervals are marked in ''italics''.
<nowiki/>* The following table assumes the 19-limit [[patent val]]; other approaches are possible. Inconsistent intervals are marked in ''italics''.


== Notation ==
== Notation ==
Line 214: Line 214:
== Approximation to JI ==
== Approximation to JI ==
{{Q-odd-limit intervals}}
{{Q-odd-limit intervals}}
=== Zeta peak index ===
{{ZPI
| zpi = 276
| steps = 56.0083399588546
| step size = 21.4253805929895
| tempered height = 6.063216
| pure height = 6.023344
| integral = 0.931117
| gap = 14.804703
| octave = 1199.82131320741
| consistent = 8
| distinct = 8
}}


== Regular temperament properties ==
== Regular temperament properties ==
Line 347: Line 333:
* [[Supra12]]
* [[Supra12]]
* Subsets of [[echidnic]][16] (6u8d):
* Subsets of [[echidnic]][16] (6u8d):
** Frankincense (this is the original/default tuning): 364.3 - 492.9 - 707.1 - 835.7 - 1200.0
** Frankincense{{idio}} (this is the original/default tuning): 364.3 - 492.9 - 707.1 - 835.7 - 1200.0
** Quasi-[[equipentatonic]]: 257.1 - 492.9 - 707.1 - 964.3 - 1200.0
** Quasi-[[equipentatonic]]: 257.1 - 492.9 - 707.1 - 964.3 - 1200.0
** Sakura-like scale containing [[phi]]: 107.1 - 492.9 - 707.1 - 835.7 - 1200.0
** Sakura-like scale containing [[phi]]: 107.1 - 492.9 - 707.1 - 835.7 - 1200.0
Line 353: Line 339:
** Evened minor pentatonic (approximated from [[72edo]]): 321.4 - 492.9 - 685.7 - 1028.6 - 1200.0
** Evened minor pentatonic (approximated from [[72edo]]): 321.4 - 492.9 - 685.7 - 1028.6 - 1200.0


== Instruments ==
[[Lumatone mapping for 56edo|Lumatone mappings for 56edo]] are available.
== Music ==
== Music ==
; [[Bryan Deister]]
* [https://www.youtube.com/shorts/o0imqFPDh9k ''56edo''] (2023)
* [https://www.youtube.com/watch?v=xkfao6yGKGE ''Curious Light - DOORS (microtonal cover in 56edo)''] (2025)
* [https://www.youtube.com/watch?v=qzMOnS-lgWs ''Waltz in 56edo''] (2025)
; [[Budjarn Lambeth]]
; [[Budjarn Lambeth]]
* [https://www.youtube.com/watch?v=VsBXIvBZY6A ''56edo Track (Echidnic16 Scale)''] (2025)
* [https://www.youtube.com/watch?v=VsBXIvBZY6A ''56edo Track (Echidnic16 Scale)''] (2025)
Line 362: Line 356:
* [https://www.youtube.com/watch?v=s1h083BRWXU ''Canon 3-in-1 on a Ground''] (2020)
* [https://www.youtube.com/watch?v=s1h083BRWXU ''Canon 3-in-1 on a Ground''] (2020)


== See also ==
* [[Lumatone mapping for 56edo]]   
[[Category:Hemithirds]]
[[Category:Hemithirds]]
[[Category:Keen]]
[[Category:Keen]]

Latest revision as of 18:12, 21 August 2025

← 55edo 56edo 57edo →
Prime factorization 23 × 7
Step size 21.4286 ¢ 
Fifth 33\56 (707.143 ¢)
Semitones (A1:m2) 7:3 (150 ¢ : 64.29 ¢)
Consistency limit 7
Distinct consistency limit 7

56 equal divisions of the octave (abbreviated 56edo or 56ed2), also called 56-tone equal temperament (56tet) or 56 equal temperament (56et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 56 equal parts of about 21.4 ¢ each. Each step represents a frequency ratio of 21/56, or the 56th root of 2.

Theory

56edo shares its near perfect quality of classical major third with 28edo, which it doubles, while also adding a superpythagorean 5th that is a convergent towards the bronze metallic mean, following 17edo and preceding 185edo. Because it contains 28edo's major third and also has a step size very close to the syntonic comma, 56edo contains very accurate approximations of both the classic major third 5/4 and the Pythagorean major third 81/64. Unfortunately, this "Pythagorean major third" is not the major third as is stacked by fifths in 56edo.

One step of 56edo is the closest direct approximation to the syntonic comma, 81/80, with the number of directly approximated syntonic commas per octave being 55.7976. (However, note that by patent val mapping, 56edo actually maps the syntonic comma inconsistently, to two steps.) Barium temperament realizes this proximity through regular temperament theory, and is supported by notable edos like 224edo, 1848edo, and 2520edo, which is a highly composite edo.

56edo can be used to tune hemithirds, superkleismic, sycamore and keen temperaments, and using ⟨56 89 130 158] (56d) as the equal temperament val, for pajara. It provides the optimal patent val for 7-, 11- and 13-limit sycamore, and the 11-limit 56d val is close to the POTE tuning for 11-limit pajara.

Prime harmonics

Approximation of prime harmonics in 56edo
Harmonic 2 3 5 7 11 13 17 19 23 29 31
Error Absolute (¢) +0.00 +5.19 -0.60 -4.54 +5.82 -4.81 +2.19 +2.49 -6.85 -1.01 -9.32
Relative (%) +0.0 +24.2 -2.8 -21.2 +27.2 -22.5 +10.2 +11.6 -31.9 -4.7 -43.5
Steps
(reduced) 		56
(0) 		89
(33) 		130
(18) 		157
(45) 		194
(26) 		207
(39) 		229
(5) 		238
(14) 		253
(29) 		272
(48) 		277
(53)

Subsets and supersets

Since 56 factors into 23 × 7, 56edo has subset edos 2, 4, 7, 8, 14, 28.

Intervals

# Cents Approximate ratios* Ups and downs notation
0 0.0 1/1 D
1 21.4 49/48, 55/54, 56/55, 64/63 ^D, vvE♭
2 42.9 28/27, 40/39, 45/44, 50/49, 81/80 ^^D, vE♭
3 64.3 25/24, 36/35, 33/32 ^3D, E♭
4 85.7 19/18, 20/19, 21/20, 22/21 v3D♯, ^E♭
5 107.1 16/15, 17/16, 18/17 vvD♯, ^^E♭
6 128.6 15/14, 13/12, 14/13 vD♯, ^3E♭
7 150.0 12/11 D♯, v3E
8 171.4 10/9, 11/10, 21/19 ^D♯, vvE
9 192.9 19/17, 28/25 ^^D♯, vE
10 214.3 9/8, 17/15 E
11 235.7 8/7 ^E, vvF
12 257.1 7/6 ^^E, vF
13 278.6 13/11, 20/17 F
14 300.0 19/16, 25/21 ^F, vvG♭
15 321.4 6/5 ^^F, vG♭
16 342.9 11/9, 17/14 ^3F, G♭
17 364.3 16/13, 21/17, 26/21 v3F♯, ^G♭
18 385.7 5/4 vvF♯, ^^G♭
19 407.1 14/11, 19/12, 24/19 vF♯, ^3G♭
20 428.6 32/25, 33/26 F♯, v3G
21 450.0 9/7, 13/10 ^F♯, vvG
22 471.4 17/13, 21/16 ^^F♯, vG
23 492.9 4/3 G
24 514.3 35/26 ^G, vvA♭
25 535.7 15/11, 19/14, 26/19, 27/20 ^^G, vA♭
26 557.1 11/8 ^3G, A♭
27 578.6 7/5 v3G♯, ^A♭
28 600.0 17/12, 24/17 vvG♯, ^^A♭
… … … …

* The following table assumes the 19-limit patent val; other approaches are possible. Inconsistent intervals are marked in italics.

Notation

Ups and downs notation

56edo can be notated using ups and downs. Trup is equivalent to quudsharp, trudsharp is equivalent to quup, etc.

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Sharp symbol                
                 
Flat symbol              
                 

Alternatively, sharps and flats with arrows borrowed from Helmholtz–Ellis notation can be used:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
Sharp symbol  
Flat symbol

Sagittal notation

This notation uses the same sagittal sequence as 63-EDO.

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation64/6381/8033/32

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation64/6381/8033/32

Approximation to JI

The following tables show how 15-odd-limit intervals are represented in 56edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 56edo (direct approximation, even if inconsistent)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
13/7, 14/13 0.273 1.3
5/4, 8/5 0.599 2.8
11/6, 12/11 0.637 3.0
15/11, 22/15 1.236 5.8
7/5, 10/7 3.941 18.4
13/10, 20/13 4.214 19.7
7/4, 8/7 4.540 21.2
11/9, 18/11 4.551 21.2
15/8, 16/15 4.588 21.4
13/8, 16/13 4.813 22.5
3/2, 4/3 5.188 24.2
5/3, 6/5 5.787 27.0
11/8, 16/11 5.825 27.2
13/9, 18/13 6.239 29.1
11/10, 20/11 6.424 30.0
9/7, 14/9 6.513 30.4
15/14, 28/15 9.129 42.6
15/13, 26/15 9.402 43.9
7/6, 12/7 9.728 45.4
13/12, 24/13 10.001 46.7
11/7, 14/11 10.365 48.4
9/8, 16/9 10.376 48.4
9/5, 10/9 10.453 48.8
13/11, 22/13 10.638 49.6
15-odd-limit intervals in 56edo (patent val mapping)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
13/7, 14/13 0.273 1.3
5/4, 8/5 0.599 2.8
11/6, 12/11 0.637 3.0
15/11, 22/15 1.236 5.8
7/5, 10/7 3.941 18.4
13/10, 20/13 4.214 19.7
7/4, 8/7 4.540 21.2
11/9, 18/11 4.551 21.2
15/8, 16/15 4.588 21.4
13/8, 16/13 4.813 22.5
3/2, 4/3 5.188 24.2
5/3, 6/5 5.787 27.0
11/8, 16/11 5.825 27.2
11/10, 20/11 6.424 30.0
15/14, 28/15 9.129 42.6
15/13, 26/15 9.402 43.9
7/6, 12/7 9.728 45.4
13/12, 24/13 10.001 46.7
11/7, 14/11 10.365 48.4
9/8, 16/9 10.376 48.4
13/11, 22/13 10.638 49.6
9/5, 10/9 10.975 51.2
9/7, 14/9 14.916 69.6
13/9, 18/13 15.189 70.9

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3 [89 -56⟩ [⟨56 89]] −1.64 1.63 7.64
2.3.5 2048/2025, 1953125/1889568 [⟨56 89 130]] −1.01 1.61 7.50
2.3.5.7 686/675, 875/864, 1029/1024 [⟨56 89 130 157]] −0.352 1.80 8.38
2.3.5.7.11 100/99, 245/242, 385/384, 686/675 [⟨56 89 130 157 194]] −0.618 1.69 7.90
2.3.5.7.11.13 91/90, 100/99, 169/168, 245/242, 385/384 [⟨56 89 130 157 194 207]] −0.299 1.70 7.95

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods
per 8ve 		Generator* Cents* Associated
ratio* 		Temperament
1 3\56 64.29 25/24 Sycamore
1 9\56 192.86 28/25 Hemithirds
1 11\56 235.71 8/7 Slendric
1 15\56 321.43 6/5 Superkleismic
1 25\56 535.71 15/11 Maquila (56d) / maquiloid (56)
2 11\56 235.71 8/7 Echidnic
2 23\56
(5\56) 		492.86
(107.14) 		4/3
(17/16) 		Keen / keenic
4 23\56
(5\56) 		492.86
(107.14) 		4/3
(17/16) 		Bidia (7-limit)
7 23\56
(1\56) 		492.86
(21.43) 		4/3
(250/243) 		Sevond

* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct

Scales

  • Supra7
  • Supra12
  • Subsets of echidnic[16] (6u8d):
    • Frankincense[idiosyncratic term] (this is the original/default tuning): 364.3 - 492.9 - 707.1 - 835.7 - 1200.0
    • Quasi-equipentatonic: 257.1 - 492.9 - 707.1 - 964.3 - 1200.0
    • Sakura-like scale containing phi: 107.1 - 492.9 - 707.1 - 835.7 - 1200.0
  • Subsets of sevond[14]
    • Evened minor pentatonic (approximated from 72edo): 321.4 - 492.9 - 685.7 - 1028.6 - 1200.0

Instruments

Lumatone mappings for 56edo are available.

Music

Bryan Deister
Budjarn Lambeth
Claudi Meneghin
Retrieved from "https://en.xen.wiki/index.php?title=56edo&oldid=207957"