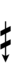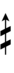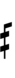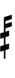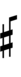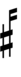51edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
BudjarnLambeth (talk | contribs)
autopatrolled
18,215 edits
m →Music: Added link
BudjarnLambeth (talk | contribs)
autopatrolled
18,215 edits
 
(30 intermediate revisions by 8 users not shown)
Line 1: Line 1:
{{Infobox ET}}
{{Infobox ET}}
{{ED intro}}


{{EDO intro|51}}
== Theory ==
Since {{nowrap|51 {{=}} 3 × 17}}, 51edo shares its [[3/2|fifth]] with [[17edo]]. Compared to other multiples of 17edo, notably [[34edo]] and [[68edo]], 51edo's harmonic inventory seems lacking, getting few harmonics very well considering its step size. However, it does possess excellent approximations of [[11/10]] and [[21/16]], only about 0.3 cents off in each case.


== Theory ==
Using the [[patent val]], 51et [[tempering out|tempers out]] [[250/243]] in the [[5-limit]], [[225/224]] and [[2401/2400]] in the [[7-limit]], and [[55/54]] and [[100/99]] in the [[11-limit]]. It is the [[optimal patent val]] for [[sonic]], the rank-3 temperament tempering out 55/54, 100/99, and 250/243, and also for the rank-4 temperament tempering out 55/54. It provides an alternative tuning to [[22edo]] for [[porcupine]], with a nice fifth but a rather flat major third, and the optimal patent val for the 7- and 11-limit [[porky]] temperament, which is sonic plus 225/224. 51 contains an archeotonic [[6L 1s]] scale based on repetitions of 8\51, creating a scale with a whole-tone-like drive towards the tonic through the 17edo semitone at the top.


{{primes in edo|51}}
Alternatively, using the 51c val {{val| 51 81 '''119''' 143 }}, the [[5/4]] is mapped to 1\3 (400 cents), [[support]]ing [[augmented]]. In the 7-limit it tempers out [[245/243]] and supports [[hemiaug]] and [[rodan]]. The 51cd val {{val| 51 81 '''119''' '''144''' }} takes the same [[7/4]] from 17edo, and supports [[augene]].  
51 EDO tempers out [[250/243]] in the [[5-limit]], [[225/224]] and [[2401/2400]] in the [[7-limit]], and [[55/54]] and [[100/99]] in the [[11-limit]]. It is the [[optimal patent val]] for [[Porcupine rank three family #Sonic|sonic]], the rank three temperament tempering out 250/243, 55/54 and 100/99, and also for the rank four temperament tempering out 55/54. It provides an alternative tuning to [[22edo]] for [[Porcupine family #Porcupine|porcupine temperament]], with a nice fifth but a rather flat major third, and the optimal patent val for 7 and 11-limit [[Porcupine family #Porky|porky temperament]], which is sonic plus 225/224. 51 contains an [[6L 1s|Archeotonic]] scale based on repetitions of 8\51, creating a scale with a whole tone-like drive towards the tonic through the 17edo semitone at the top.


51edo's step is the closest direct approximation to the [[Pythagorean comma]] by edo steps, though that comma itself is mapped to a different interval.
51edo's step is the closest direct approximation to the [[Pythagorean comma]] by edo steps, though that comma itself is mapped to a different interval.
=== Odd harmonics ===
{{Harmonics in equal|51}}
=== Subsets and supersets ===
51edo contains [[3edo]] and [[17edo]] as subsets.
One of the very powerful (but very complex) supersets of 51edo is [[612edo]], which divides each step of 51edo into 12 equal parts, for which the name "skisma" has been proposed.


== Intervals ==
== Intervals ==
{| class="wikitable center-all right-2 left-3"
{| class="wikitable center-all right-2 left-3"
|-
|-
! Degrees
! #
! [[Cents|Cents]]
! [[Cent]]s
! colspan="3" | [[Ups and Downs Notation]]
! colspan="3" | [[Ups and downs notation]]
|-
|-
| 0
| 0
| 0.000
| 0.0
| Perfect 1sn
| Perfect 1sn
| P1
| P1
Line 25: Line 33:
|-
|-
| 1
| 1
| 23.529
| 23.5
| Up 1sn
| Up 1sn
| ^1
| ^1
Line 31: Line 39:
|-
|-
| 2
| 2
| 47.059
| 47.1
| Downminor 2nd
| Downminor 2nd
| vm2
| vm2
Line 37: Line 45:
|-
|-
| 3
| 3
| 70.588
| 70.6
| Minor 2nd
| Minor 2nd
| m2
| m2
Line 43: Line 51:
|-
|-
| 4
| 4
| 94.118
| 94.1
| Upminor 2nd
| Upminor 2nd
| ^m2
| ^m2
Line 49: Line 57:
|-
|-
| 5
| 5
| 117.647
| 117.6
| Downmid 2nd
| Downmid 2nd
| v~2
| v~2
Line 55: Line 63:
|-
|-
| 6
| 6
| 141.176
| 141.2
| Mid 2nd
| Mid 2nd
| ~2
| ~2
Line 61: Line 69:
|-
|-
| 7
| 7
| 164.706
| 164.7
| Upmid 2nd
| Upmid 2nd
| ^~2
| ^~2
Line 67: Line 75:
|-
|-
| 8
| 8
| 188.235
| 188.2
| Downmajor 2nd
| Downmajor 2nd
| vM2
| vM2
Line 73: Line 81:
|-
|-
| 9
| 9
| 211.765
| 211.8
| Major 2nd
| Major 2nd
| M2
| M2
Line 79: Line 87:
|-
|-
| 10
| 10
| 235.294
| 235.3
| Upmajor 2nd
| Upmajor 2nd
| ^M2
| ^M2
Line 85: Line 93:
|-
|-
| 11
| 11
| 258.824
| 258.8
| Downminor 3rd
| Downminor 3rd
| vm3
| vm3
Line 91: Line 99:
|-
|-
| 12
| 12
| 282.353
| 282.4
| Minor 3rd
| Minor 3rd
| m3
| m3
Line 97: Line 105:
|-
|-
| 13
| 13
| 305.882
| 305.9
| Upminor 3rd
| Upminor 3rd
| ^m3
| ^m3
Line 103: Line 111:
|-
|-
| 14
| 14
| 329.412
| 329.4
| Downmid 3rd
| Downmid 3rd
| v~3
| v~3
Line 109: Line 117:
|-
|-
| 15
| 15
| 352.941
| 352.9
| Mid 3rd
| Mid 3rd
| ~3
| ~3
Line 115: Line 123:
|-
|-
| 16
| 16
| 376.471
| 376.5
| Upmid 3rd
| Upmid 3rd
| ^~3
| ^~3
Line 121: Line 129:
|-
|-
| 17
| 17
| 400.000
| 400.0
| Downmajor 3rd
| Downmajor 3rd
| vM3
| vM3
Line 127: Line 135:
|-
|-
| 18
| 18
| 423.529
| 423.5
| Major 3rd
| Major 3rd
| M3
| M3
Line 133: Line 141:
|-
|-
| 19
| 19
| 447.509
| 447.1
| Upmajor 3rd
| Upmajor 3rd
| ^M3
| ^M3
Line 139: Line 147:
|-
|-
| 20
| 20
| 470.588
| 470.6
| Down 4th
| Down 4th
| v4
| v4
Line 145: Line 153:
|-
|-
| 21
| 21
| 494.118
| 494.1
| Perfect 4th
| Perfect 4th
| P4
| P4
Line 151: Line 159:
|-
|-
| 22
| 22
| 517.647
| 517.6
| Up 4th
| Up 4th
| ^4
| ^4
Line 157: Line 165:
|-
|-
| 23
| 23
| 541.176
| 541.2
| Downdim 5th
| Downdim 5th
| vd5
| vd5
Line 163: Line 171:
|-
|-
| 24
| 24
| 564.706
| 564.7
| Dim 5th
| Dim 5th
| d5
| d5
Line 169: Line 177:
|-
|-
| 25
| 25
| 588.235
| 588.2
| Updim 5th
| Updim 5th
| ^d5
| ^d5
Line 175: Line 183:
|-
|-
| 26
| 26
| 611.765
| 611.8
| Downaug 4th
| Downaug 4th
| vA4
| vA4
Line 181: Line 189:
|-
|-
| 27
| 27
| 635.294
| 635.3
| Aug 4th
| Aug 4th
| A4
| A4
Line 187: Line 195:
|-
|-
| 28
| 28
| 658.824
| 658.8
| Upaug 4th
| Upaug 4th
| ^A4
| ^A4
Line 193: Line 201:
|-
|-
| 29
| 29
| 682.353
| 682.4
| Down 5th
| Down 5th
| v5
| v5
Line 199: Line 207:
|-
|-
| 30
| 30
| 705.882
| 705.9
| Perfect 5th
| Perfect 5th
| P5
| P5
Line 205: Line 213:
|-
|-
| 31
| 31
| 729.412
| 729.4
| Up 5th
| Up 5th
| ^5
| ^5
Line 211: Line 219:
|-
|-
| 32
| 32
| 752.941
| 752.9
| Downminor 6th
| Downminor 6th
| vm6
| vm6
Line 217: Line 225:
|-
|-
| 33
| 33
| 776.471
| 776.5
| Minor 6th
| Minor 6th
| m6
| m6
Line 223: Line 231:
|-
|-
| 34
| 34
| 800.000
| 800.0
| Upminor 6th
| Upminor 6th
| ^m6
| ^m6
Line 229: Line 237:
|-
|-
| 35
| 35
| 823.529
| 823.5
| Downmid 6th
| Downmid 6th
| v~6
| v~6
Line 235: Line 243:
|-
|-
| 36
| 36
| 847.059
| 847.1
| Mid 6th
| Mid 6th
| ~6
| ~6
Line 241: Line 249:
|-
|-
| 37
| 37
| 870.588
| 870.6
| Upmid 6th
| Upmid 6th
| ^~6
| ^~6
Line 247: Line 255:
|-
|-
| 38
| 38
| 894.118
| 894.1
| Downmajor 6th
| Downmajor 6th
| vM6
| vM6
Line 253: Line 261:
|-
|-
| 39
| 39
| 917.647
| 917.6
| Major 6th
| Major 6th
| M6
| M6
Line 259: Line 267:
|-
|-
| 40
| 40
| 941.176
| 941.2
| Upmajor 6th
| Upmajor 6th
| ^M6
| ^M6
Line 265: Line 273:
|-
|-
| 41
| 41
| 964.706
| 964.7
| Downminor 7th
| Downminor 7th
| vm7
| vm7
Line 271: Line 279:
|-
|-
| 42
| 42
| 988.235
| 988.2
| Minor 7th
| Minor 7th
| m7
| m7
Line 277: Line 285:
|-
|-
| 43
| 43
| 1011.765
| 1011.8
| Upminor 7th
| Upminor 7th
| ^m7
| ^m7
Line 283: Line 291:
|-
|-
| 44
| 44
| 1035.294
| 1035.3
| Downmid 7th
| Downmid 7th
| v~7
| v~7
Line 289: Line 297:
|-
|-
| 45
| 45
| 1058.824
| 1058.8
| Mid 7th
| Mid 7th
| ~7
| ~7
Line 295: Line 303:
|-
|-
| 46
| 46
| 1082.353
| 1082.4
| Upmid 7th
| Upmid 7th
| ^~7
| ^~7
Line 301: Line 309:
|-
|-
| 47
| 47
| 1105.882
| 1105.9
| Downmajor 7th
| Downmajor 7th
| vM7
| vM7
Line 307: Line 315:
|-
|-
| 48
| 48
| 1129.412
| 1129.4
| Major 7th
| Major 7th
| M7
| M7
Line 313: Line 321:
|-
|-
| 49
| 49
| 1152.941
| 1152.9
| Upmajor 7th
| Upmajor 7th
| ^M7
| ^M7
Line 319: Line 327:
|-
|-
| 50
| 50
| 1176.471
| 1176.5
| Down 8ve
| Down 8ve
| v8
| v8
Line 325: Line 333:
|-
|-
| 51
| 51
| 1200.000
| 1200.0
| Perfect 8ve
| Perfect 8ve
| P8
| P8
| D
| D
|}
|}
== Notation ==
=== Ups and downs notation ===
51edo can be notated with ups and downs, spoken as up, dup, trup, dudsharp, downsharp, sharp, upsharp etc. and down, dud, trud, dupflat etc.
{{Sharpness-sharp6a}}
Half-sharps and half-flats can be used to avoid triple arrows:
{{Sharpness-sharp6b}}
In 51edo, a combination of quarter tone accidentals and arrow accidentals from [[Helmholtz–Ellis notation]] can be used.
{{Sharpness-sharp6}}
If double arrows are not desirable, then arrows can be attached to quarter-tone accidentals:
{{Sharpness-sharp6-qt}}
=== Ivan Wyschnegradsky's notation ===
Since a sharp raises by six steps, Wyschnegradsky accidentals borrowed from [[72edo]] can also be used:
{{Sharpness-sharp6-iw}}
=== Sagittal notation ===
In the following diagrams, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's [[Sagittal notation#Primary comma|primary comma]] (the comma it ''exactly'' represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it ''approximately'' represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this edo.
==== Evo flavor ====
<imagemap>
File:51-EDO_Evo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 519 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 120 106 [[64/63]]
rect 120 80 220 106 [[81/80]]
rect 220 80 340 106 [[27/26]]
</imagemap>
==== Revo flavor ====
<imagemap>
File:51-EDO_Revo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 511 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 120 106 [[64/63]]
rect 120 80 220 106 [[81/80]]
rect 220 80 340 106 [[27/26]]
default [[File:51-EDO_Revo_Sagittal.svg]]
</imagemap>
==== Evo-SZ flavor ====
<imagemap>
File:51-EDO_Evo-SZ_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 511 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 120 106 [[64/63]]
rect 120 80 220 106 [[81/80]]
rect 220 80 340 106 [[27/26]]
default [[File:51-EDO_Evo-SZ_Sagittal.svg]]
</imagemap>
== Regular temperament properties ==
{| class="wikitable center-4 center-5 center-6"
|-
! rowspan="2" | [[Subgroup]]
! rowspan="2" | [[Comma list]]
! rowspan="2" | [[Mapping]]
! rowspan="2" | Optimal<br>8ve stretch (¢)
! colspan="2" | Tuning error
|-
! [[TE error|Absolute]] (¢)
! [[TE simple badness|Relative]] (%)
|-
| 2.3.7
| 1029/1024, {{monzo| 17 -16 3 }}
| {{Mapping| 51 81 143 }}
| −0.339
| 1.63
| 6.92
|- style="border-top: double;"
| 2.3.5
| 128/125, {{monzo| -13 17 -6 }}
| {{Mapping| 51 81 119 }} (51c)
| −2.789
| 2.41
| 10.3
|- style="border-top: double;"
| 2.3.5
| 250/243, 34171875/33554432
| {{Mapping| 51 81 118 }} (51)
| +0.581
| 2.77
| 11.8
|}
=== Rank-2 temperaments ===
{| class="wikitable center-all left-5"
|+ style="font-size: 105%;" | Table of rank-2 temperaments by generator
|-
! Periods<br>per 8ve
! Generator*
! Cents*
! Associated<br>ratio*
! Temperament
|-
| 1
| 5\51
| 117.6
| 15/14
| [[Miracle]] (51e, out of tune) / oracle (51)
|-
| 1
| 7\51
| 164.7
| 11/10
| [[Porky]] (51)
|-
| 1
| 10\51
| 235.3
| 8/7
| [[Rodan]] (51cf…, out of tune) / aerodino (51ce)
|-
| 1
| 5\51
| 541.2
| 15/11
| [[Necromanteion]] (51ce)
|-
| 3
| 19\51<br>(2\51)
| 447.1<br>(47.1)
| 9/7<br>(36/35)
| [[Hemiaug]] (51ce)
|-
| 3
| 21\51<br>(4\51)
| 494.1<br>(94.1)
| 4/3<br>(16/15)
| [[Augmented]] (51c)
|}
<nowiki/>* [[Normal lists|Octave-reduced form]], reduced to the first half-octave, and [[normal lists|minimal form]] in parentheses if distinct
== Scales ==
* [[Porky]][7] (Palace{{idio}}): 7 7 7 9 7 7 7
* UFO scale{{idio}} ([[inflected MOS]] of [[Batch 89 temperaments#Teefs|Teefs]][19]{{idio}}): 2 2 4 1 2 2 2 4 2 5 2 4 4 2 2 1 4 2 2
* Cosmic scale{{idio}} subset of UFO scale): 21 9 4 9 8
== Instruments ==
; Lumatone
: See [[Lumatone mapping for 51edo]].


== Music ==
== Music ==
'''[[Frédéric Gagné]]'''
; [[Bryan Deister]]
* [https://youtu.be/_E6qvbJWYY8 ''Whalectric''] (2022)
* [https://www.youtube.com/shorts/5pM8OC0fV98 ''51edo improv''] (2025)
 
; [[Frédéric Gagné]]
* ''Whalectric'' (2022) – [https://youtu.be/_E6qvbJWYY8 YouTube] | [https://musescore.com/fredg999/whalectric score] – 7:4 [[semiquartal]] 4|4 mode


'''[[James Mulvale]] (FAST-fast)'''
; [[James Mulvale]] (FASTFAST)
* [https://youtu.be/8GojBZSyqDw ''STARS (Thoughts and Prayers)''] (51 EDO for 51 States) (2020)
* [https://youtu.be/8GojBZSyqDw ''STARS (Thoughts and Prayers)''] (2020)


'''[[Ray Perlner]]'''
; [[Ray Perlner]]
* [https://www.youtube.com/watch?v=peidZ1jEafQ ''<nowiki>Fugue for Organ in 51EDO Porcupine[7] ssssssL “Pandian”</nowiki>''] (2023)
* [https://www.youtube.com/watch?v=peidZ1jEafQ ''Fugue''] (2023) – for organ in 51edo Porcupine[7] ssssssL "Pandian"


[[Category:51edo]]
[[Category:Listen]]
[[Category:Equal divisions of the octave|##]] <!-- 2-digit number -->

Latest revision as of 23:33, 16 August 2025

← 50edo 51edo 52edo →
Prime factorization 3 × 17
Step size 23.5294 ¢ 
Fifth 30\51 (705.882 ¢) (→ 10\17)
Semitones (A1:m2) 6:3 (141.2 ¢ : 70.59 ¢)
Consistency limit 3
Distinct consistency limit 3

51 equal divisions of the octave (abbreviated 51edo or 51ed2), also called 51-tone equal temperament (51tet) or 51 equal temperament (51et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 51 equal parts of about 23.5 ¢ each. Each step represents a frequency ratio of 21/51, or the 51st root of 2.

Theory

Since 51 = 3 × 17, 51edo shares its fifth with 17edo. Compared to other multiples of 17edo, notably 34edo and 68edo, 51edo's harmonic inventory seems lacking, getting few harmonics very well considering its step size. However, it does possess excellent approximations of 11/10 and 21/16, only about 0.3 cents off in each case.

Using the patent val, 51et tempers out 250/243 in the 5-limit, 225/224 and 2401/2400 in the 7-limit, and 55/54 and 100/99 in the 11-limit. It is the optimal patent val for sonic, the rank-3 temperament tempering out 55/54, 100/99, and 250/243, and also for the rank-4 temperament tempering out 55/54. It provides an alternative tuning to 22edo for porcupine, with a nice fifth but a rather flat major third, and the optimal patent val for the 7- and 11-limit porky temperament, which is sonic plus 225/224. 51 contains an archeotonic 6L 1s scale based on repetitions of 8\51, creating a scale with a whole-tone-like drive towards the tonic through the 17edo semitone at the top.

Alternatively, using the 51c val ⟨51 81 119 143], the 5/4 is mapped to 1\3 (400 cents), supporting augmented. In the 7-limit it tempers out 245/243 and supports hemiaug and rodan. The 51cd val ⟨51 81 119 144] takes the same 7/4 from 17edo, and supports augene.

51edo's step is the closest direct approximation to the Pythagorean comma by edo steps, though that comma itself is mapped to a different interval.

Odd harmonics

Approximation of prime harmonics in 51edo
Harmonic 2 3 5 7 11 13 17 19 23 29 31
Error Absolute (¢) +0.0 +3.9 -9.8 -4.1 -10.1 +6.5 -10.8 +8.4 +7.0 +5.7 +7.9
Relative (%) +0.0 +16.7 -41.8 -17.5 -43.1 +27.8 -46.1 +35.6 +29.8 +24.3 +33.6
Steps
(reduced) 		51
(0) 		81
(30) 		118
(16) 		143
(41) 		176
(23) 		189
(36) 		208
(4) 		217
(13) 		231
(27) 		248
(44) 		253
(49)

Subsets and supersets

51edo contains 3edo and 17edo as subsets.

One of the very powerful (but very complex) supersets of 51edo is 612edo, which divides each step of 51edo into 12 equal parts, for which the name "skisma" has been proposed.

Intervals

# Cents Ups and downs notation
0 0.0 Perfect 1sn P1 D
1 23.5 Up 1sn ^1 ^D
2 47.1 Downminor 2nd vm2 vEb
3 70.6 Minor 2nd m2 Eb
4 94.1 Upminor 2nd ^m2 ^Eb
5 117.6 Downmid 2nd v~2 ^^Eb
6 141.2 Mid 2nd ~2 vvvE, ^^^Eb
7 164.7 Upmid 2nd ^~2 vvE
8 188.2 Downmajor 2nd vM2 vE
9 211.8 Major 2nd M2 E
10 235.3 Upmajor 2nd ^M2 ^E
11 258.8 Downminor 3rd vm3 vF
12 282.4 Minor 3rd m3 F
13 305.9 Upminor 3rd ^m3 ^F
14 329.4 Downmid 3rd v~3 ^^F
15 352.9 Mid 3rd ~3 ^^^F, vvvF#
16 376.5 Upmid 3rd ^~3 vvF#
17 400.0 Downmajor 3rd vM3 vF#
18 423.5 Major 3rd M3 F#
19 447.1 Upmajor 3rd ^M3 ^F#
20 470.6 Down 4th v4 vG
21 494.1 Perfect 4th P4 G
22 517.6 Up 4th ^4 ^G
23 541.2 Downdim 5th vd5 vAb
24 564.7 Dim 5th d5 Ab
25 588.2 Updim 5th ^d5 ^Ab
26 611.8 Downaug 4th vA4 vG#
27 635.3 Aug 4th A4 G#
28 658.8 Upaug 4th ^A4 ^G#
29 682.4 Down 5th v5 vA
30 705.9 Perfect 5th P5 A
31 729.4 Up 5th ^5 ^A
32 752.9 Downminor 6th vm6 vBb
33 776.5 Minor 6th m6 Bb
34 800.0 Upminor 6th ^m6 ^Bb
35 823.5 Downmid 6th v~6 ^^Bb
36 847.1 Mid 6th ~6 vvvB, ^^^Bb
37 870.6 Upmid 6th ^~6 vvB
38 894.1 Downmajor 6th vM6 vB
39 917.6 Major 6th M6 B
40 941.2 Upmajor 6th ^M6 ^B
41 964.7 Downminor 7th vm7 vC
42 988.2 Minor 7th m7 C
43 1011.8 Upminor 7th ^m7 ^C
44 1035.3 Downmid 7th v~7 ^^C
45 1058.8 Mid 7th ~7 ^^^C, vvvC#
46 1082.4 Upmid 7th ^~7 vvC#
47 1105.9 Downmajor 7th vM7 vC#
48 1129.4 Major 7th M7 C#
49 1152.9 Upmajor 7th ^M7 ^C#
50 1176.5 Down 8ve v8 vD
51 1200.0 Perfect 8ve P8 D

Notation

Ups and downs notation

51edo can be notated with ups and downs, spoken as up, dup, trup, dudsharp, downsharp, sharp, upsharp etc. and down, dud, trud, dupflat etc.

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12
Sharp symbol
         
             
Flat symbol          
             

Half-sharps and half-flats can be used to avoid triple arrows:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12
Sharp symbol
 
    
    
    
Flat symbol  
    
    
    

In 51edo, a combination of quarter tone accidentals and arrow accidentals from Helmholtz–Ellis notation can be used.

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Sharp symbol  
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
Flat symbol  
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 

If double arrows are not desirable, then arrows can be attached to quarter-tone accidentals:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13
Sharp symbol
 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
Flat symbol  
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 

Ivan Wyschnegradsky's notation

Since a sharp raises by six steps, Wyschnegradsky accidentals borrowed from 72edo can also be used:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13
Sharp symbol
 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 
  
 		 
Flat symbol  
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
 

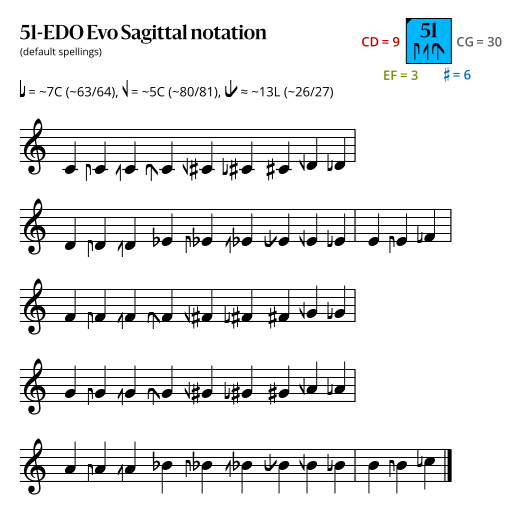
Sagittal notation

In the following diagrams, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's primary comma (the comma it exactly represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it approximately represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this edo.

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation64/6381/8027/26

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation64/6381/8027/26

Evo-SZ flavor

Sagittal notationPeriodic table of EDOs with sagittal notation64/6381/8027/26

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3.7 1029/1024, [17 -16 3⟩ [⟨51 81 143]] −0.339 1.63 6.92
2.3.5 128/125, [-13 17 -6⟩ [⟨51 81 119]] (51c) −2.789 2.41 10.3
2.3.5 250/243, 34171875/33554432 [⟨51 81 118]] (51) +0.581 2.77 11.8

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods
per 8ve 		Generator* Cents* Associated
ratio* 		Temperament
1 5\51 117.6 15/14 Miracle (51e, out of tune) / oracle (51)
1 7\51 164.7 11/10 Porky (51)
1 10\51 235.3 8/7 Rodan (51cf…, out of tune) / aerodino (51ce)
1 5\51 541.2 15/11 Necromanteion (51ce)
3 19\51
(2\51) 		447.1
(47.1) 		9/7
(36/35) 		Hemiaug (51ce)
3 21\51
(4\51) 		494.1
(94.1) 		4/3
(16/15) 		Augmented (51c)

* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct

Scales

Instruments

Lumatone
See Lumatone mapping for 51edo.

Music

Bryan Deister
Frédéric Gagné
James Mulvale (FASTFAST)
Ray Perlner
  • Fugue (2023) – for organ in 51edo Porcupine[7] ssssssL "Pandian"
Retrieved from "https://en.xen.wiki/index.php?title=51edo&oldid=207207"