Marvel: Difference between revisions
→Tunings: rework: this analysis is so at odds with everyone else's, as we've long found 197- and 240edo to be optimal edo tunings in the 7-limit, which is very well documented. The idea of not targeting 7-odd-limit intervals in favor of complex 5-limit intervals is very sus; the facts about 53edo and 84edo are also wrong, with 125edo missing, and the constraint of consistency is so arbitrary that it seems to be there just to single out the edos you like |
m →Other marvel scales: add link to orphaned page |
||
| (11 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
'''Marvel''' is | '''Marvel''' is a [[rank-3 temperament|rank-3]] [[regular temperament|temperament]] with the same [[lattice]] structure as [[5-limit]] [[JI]], while identifying the [[7/4|harmonic seventh (7/4)]] as a stack of two [[15/8|classical major sevenths (15/8)]] [[octave reduction|octave-reduced]], [[tempering out]] [[225/224]]. It is the head of the [[marvel family]], and the canonical [[11-limit]] [[extension]] adding [[385/384]] and [[540/539]] to the comma list makes it a member of both [[keenanismic temperaments|keenansimic]] and [[swetismic temperaments]]. | ||
The temperament was named by [[Gene Ward Smith]] in 2002–2003, when the 11-limit version was found first<ref>[https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_5145.html#5184 Yahoo! Tuning Group | ''Relative complexity and scale construction''] – first mention of ''marvel''.</ref><ref>[https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_5687.html Yahoo! Tuning Group | ''Top 135 11-limit planar temperaments''] – establishment as an 11-limit temperament.</ref>. Gene carried it to the 7-limit restriction in 2004<ref>[https://yahootuninggroupsultimatebackup.github.io/tuning/topicId_50829.html Yahoo! Tuning Group | ''Marvel'']</ref>. | The temperament was named by [[Gene Ward Smith]] in 2002–2003, when the 11-limit version was found first<ref>[https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_5145.html#5184 Yahoo! Tuning Group | ''Relative complexity and scale construction''] – first mention of ''marvel''.</ref><ref>[https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_5687.html Yahoo! Tuning Group | ''Top 135 11-limit planar temperaments''] – establishment as an 11-limit temperament.</ref>. Gene carried it to the 7-limit restriction in 2004<ref>[https://yahootuninggroupsultimatebackup.github.io/tuning/topicId_50829.html Yahoo! Tuning Group | ''Marvel'']</ref>. | ||
| Line 78: | Line 78: | ||
* [[Pump17]] | * [[Pump17]] | ||
* [[Pump18]] | * [[Pump18]] | ||
* [[Diamond9plus-marvel]] | |||
== Tunings == | == Tunings == | ||
In the 7-limit, the optimal way such as that taken by [[TE]] and derivatives to close out the comma 225/224 is to tune primes 3 and 5 flat, and 2 and 7 sharp. If we tune the octave pure, the other inclinations remain. This indicates that the diminished third [[~]][[256/225]] should be sharp (towards [[~]][[8/7]]), the augmented second [[~]][[75/64]] be flat (towards [[~]][[7/6]]), the diminished fourth [[~]][[32/25]] be sharp (towards [[~]][[9/7]]) and the tritone [[~]][[45/32]] be flat (towards [[~]][[7/5]]), such that every [[7-limit]] [[9-odd-limit]] interval is tuned between itself and the [[5-limit]] interpretation it is separated from by [[225/224]]. If we take these as hard constraints, then [[53edo]] and [[84edo]] are the smallest edo tunings to satisfy them, but if overtempering is allowed, many smaller edos are possible, such as [[31edo|31-]] and [[41edo]]. Interestingly, [[72edo]], though very performant as a 7- and 11-limit tuning, is overtempered for some of these constraints, whereas 53edo, though satisfying these constraints, tempers the intervals closer to the more complex [[5-limit]] interpretations, though the 7-limit concordances of the 9-odd-limit still clearly work. [[84edo]], another superset of 12edo, is an interesting edo to look at for its high performance in large odd-limits. Going up to larger edos, [[125edo|125-]], [[166edo|166-]], [[178edo|178-]], [[197edo|197-]], and [[240edo]] are all great choices with different intonational characteristics. | |||
[[ | The marvel extension [[hecate]] has the no-17's [[19-limit]] as its subgroup, and tridecimal marvel, the extension chosen by [[Gene Ward Smith]], is in the 13-limit. They merge in the rank-2 temperament [[catakleismic]], which can be conceptualized as accepting both rank-3 marvel structures simultaneously. One such tuning is excellently given by [[125edo]]. If we are looking for a small edo tuning instead, 53edo and 72edo are also reasonable edo tunings for the full no-17's 19-limit catakleismic, though in 53edo the 11 and 19 are a little off and in 72edo the 13 and 19 are a little off instead; 72edo is positioned better as a full [[17-limit]] marvel system while 53edo is positioned better as a (potentially no-11's) [[13-limit]] marvel system. If we focus on the 11-limit of undecimal marvel (discarding the mapping of 13), 31edo and 41edo are the smallest to clearly succeed, though many accept 41edo's mapping of [[~]][[13/8]] to the neutral sixth and some accept that mapping for 31edo as contextually usable too. | ||
=== Tuning spectrum === | === Tuning spectrum === | ||
| Line 184: | Line 185: | ||
<references/> | <references/> | ||
[[Category:Marvel| ]] <!-- main article --> | [[Category:Marvel| ]] <!-- main article --> | ||
[[Category:Rank-3 temperaments]] | |||
[[Category:Marvel family]] | [[Category:Marvel family]] | ||
[[Category:Keenanismic temperaments]] | [[Category:Keenanismic temperaments]] | ||
[[Category:Swetismic temperaments]] | [[Category:Swetismic temperaments]] | ||
Latest revision as of 07:51, 7 June 2025
Marvel is a rank-3 temperament with the same lattice structure as 5-limit JI, while identifying the harmonic seventh (7/4) as a stack of two classical major sevenths (15/8) octave-reduced, tempering out 225/224. It is the head of the marvel family, and the canonical 11-limit extension adding 385/384 and 540/539 to the comma list makes it a member of both keenansimic and swetismic temperaments.
The temperament was named by Gene Ward Smith in 2002–2003, when the 11-limit version was found first[1][2]. Gene carried it to the 7-limit restriction in 2004[3].
Extending marvel to the 13-limit is not as obvious. While Gene has chosen 351/350 as the canonical extension, hecate, tempering out 325/324 and 729/728, arguably makes more sense as it is closer in tuning[4]. Hecate has a natural extension to the no-17 19-limit, by tempering out 400/399 and 513/512.
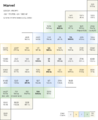
See Marvel family #Marvel for technical data.
Interval lattice
-
11-limit marvel
-
13-limit marvel/hecate
-
2.3.5.7.11.13.19 subgroup marvel/hecate
Notation
Marvel can be notated the same as 5-limit just intonation since they share the same lattice structure. One way to do this is to take the conventional circle-of-fifths notation with an additional module of accidentals for the 81/80 comma. In this system, 5/4 is a major third, 7/4 an augmented sixth, and 11/8 a double diminished 5th.
| Ratio | Nominal | Example |
|---|---|---|
| 3/2 | Perfect fifth | C-G |
| 5/4 | Down major third | C-vE |
| 7/4 | Dudaugmented sixth | C-vvA# |
| 11/8 | Trup double-diminished fifth | C-^3Gbb |
| 13/8 | Dup minor sixth | C-^^Ab |
| 19/16 | Minor third | C-Eb |
Alternatively, it can be notated the same as full prime-limit just intonation, with a distinct accidental pair for each prime. That makes some intervals more intuitive, at the cost of hiding the structure of marvel tempering. For example, it is customary of the 5/4 to be a major third, and 7/4 to be a minor seventh. As a result, the fact that the 14/9 is a stack of two 5/4's is not revealed, and the related chords can be less convenient.
Chords
Marvel enables essentially tempered chords of marvel, keenanismic, swetismic, and undecimal marvel. Extending the temperament to the 13-limit through 325/324, resulting in hecate, enables chords of marveltwin and squbemic. Hecate hexad is a chord peculiar to this temperament.
Alternative 11-limit extensions give different sets of chords. One notable example, tempering out 441/440, enables prodigy chords.
Scales
Marvel hobbit scales
Undecimal marvel hobbit scales
Other marvel scales
Tunings
In the 7-limit, the optimal way such as that taken by TE and derivatives to close out the comma 225/224 is to tune primes 3 and 5 flat, and 2 and 7 sharp. If we tune the octave pure, the other inclinations remain. This indicates that the diminished third ~256/225 should be sharp (towards ~8/7), the augmented second ~75/64 be flat (towards ~7/6), the diminished fourth ~32/25 be sharp (towards ~9/7) and the tritone ~45/32 be flat (towards ~7/5), such that every 7-limit 9-odd-limit interval is tuned between itself and the 5-limit interpretation it is separated from by 225/224. If we take these as hard constraints, then 53edo and 84edo are the smallest edo tunings to satisfy them, but if overtempering is allowed, many smaller edos are possible, such as 31- and 41edo. Interestingly, 72edo, though very performant as a 7- and 11-limit tuning, is overtempered for some of these constraints, whereas 53edo, though satisfying these constraints, tempers the intervals closer to the more complex 5-limit interpretations, though the 7-limit concordances of the 9-odd-limit still clearly work. 84edo, another superset of 12edo, is an interesting edo to look at for its high performance in large odd-limits. Going up to larger edos, 125-, 166-, 178-, 197-, and 240edo are all great choices with different intonational characteristics.
The marvel extension hecate has the no-17's 19-limit as its subgroup, and tridecimal marvel, the extension chosen by Gene Ward Smith, is in the 13-limit. They merge in the rank-2 temperament catakleismic, which can be conceptualized as accepting both rank-3 marvel structures simultaneously. One such tuning is excellently given by 125edo. If we are looking for a small edo tuning instead, 53edo and 72edo are also reasonable edo tunings for the full no-17's 19-limit catakleismic, though in 53edo the 11 and 19 are a little off and in 72edo the 13 and 19 are a little off instead; 72edo is positioned better as a full 17-limit marvel system while 53edo is positioned better as a (potentially no-11's) 13-limit marvel system. If we focus on the 11-limit of undecimal marvel (discarding the mapping of 13), 31edo and 41edo are the smallest to clearly succeed, though many accept 41edo's mapping of ~13/8 to the neutral sixth and some accept that mapping for 31edo as contextually usable too.
Tuning spectrum
This spectrum assumes pure 2 and 7.
| Eigenmonzo (Unchanged-interval) |
Fifth (¢) |
Major Third (¢) |
Comments |
|---|---|---|---|
| 5/4 | 698.099 | 386.314 | |
| 6/5 | 700.027 | 384.386 | 7-odd-limit minimax |
| 15/11 | 700.351 | 384.062 | |
| 10/9 | 700.670 | 383.743 | 9-odd-limit minimax |
| 11/10 | 700.885 | 383.528 | |
| 15/13 | 700.916 | 383.497 | 15-odd-limit hecate minimax |
| 13/10 | 701.065 | 383.348 | 13-odd-limit hecate minimax |
| 13/11 | 701.199 | 383.214 | |
| 18/13 | 701.361 | 383.052 | |
| 13/12 | 701.480 | 382.933 | |
| 16/13 | 701.559 | 382.854 | |
| 4/3 | 701.955 | 382.458 | |
| 14/11 | 702.278 | 382.135 | |
| 11/8 | 702.278 | 382.135 | |
| 12/11 | 702.602 | 381.811 |
Music
- Pump1 – in pump12 1, 197edo tuning
- Semimarvelous Blue Drawf (2010) – in Dwarf17marv, equal-beating tuning
See also
- Marvel temperaments, the collection of rank-2 temperaments that temper out the marvel comma
Notes
- ↑ Yahoo! Tuning Group | Relative complexity and scale construction – first mention of marvel.
- ↑ Yahoo! Tuning Group | Top 135 11-limit planar temperaments – establishment as an 11-limit temperament.
- ↑ Yahoo! Tuning Group | Marvel
- ↑ Yahoo! Tuning Group | 13-limit marvel