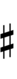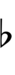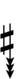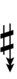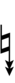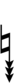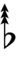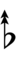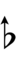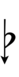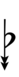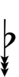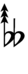42edo

← 41edo

42edo

43edo →

Prime factorization	2 × 3 × 7
Step size	28.5714 ¢
Fifth	25\42 (714.286 ¢)
Semitones (A1:m2)	7:1 (200 ¢ : 28.57 ¢)
Dual sharp fifth	25\42 (714.286 ¢)
Dual flat fifth	24\42 (685.714 ¢) (→ 4\7)
Dual major 2nd	7\42 (200 ¢) (→ 1\6)
Consistency limit	7
Distinct consistency limit	7

42 equal divisions of the octave (abbreviated 42edo or 42ed2), also called 42-tone equal temperament (42tet) or 42 equal temperament (42et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 42 equal parts of about 28.6 ¢ each. Each step represents a frequency ratio of 2^1/42, or the 42nd root of 2.

Theory

42edo has a patent val fifth (the step of which is not from 7edo, this being a first for edos of the form 7n) and a third both over 12 cents sharp, using the same 400-cent interval to represent 5/4 as does 12edo, which means it tempers out 128/125. In the 7-limit, it tempers out 64/63 and 126/125, making it a tuning supporting the augene temperament.

42edo is on the optimal ET sequence of the eugene, joan, lemba, neutron, qeema, seville, sevond, skateboard, tritikleismic and vines temperaments.

42edo is a diatonic edo because its 5th falls between 4\7 = 686 ¢ and 3\5 = 720 ¢. 42edo is one of the most difficult diatonic edos to notate, because no other diatonic edo's fifth is as sharp (see 47edo for the opposite extreme).

Odd harmonics

While not an accurate tuning on the full 7-limit, 42edo does an excellent job on the 2.9.15.7.33.39 2*42 subgroup, having the same tuning on it as does 84edo. On this subgroup 42 has the same commas as 84.

Approximation of odd harmonics in 42edo

Harmonic		3	5	7	9	11	13	15	17	19	21	23
Error	Absolute (¢)	+12.3	+13.7	+2.6	-3.9	-8.5	-12.0	-2.6	+9.3	-11.8	-13.6	+0.3
	Relative (%)	+43.2	+47.9	+9.1	-13.7	-29.6	-41.8	-8.9	+32.7	-41.3	-47.7	+1.0
Steps (reduced)		67 (25)	98 (14)	118 (34)	133 (7)	145 (19)	155 (29)	164 (38)	172 (4)	178 (10)	184 (16)	190 (22)

Subsets and supersets

Since 42 factors into 2 × 3 × 7, 42edo contains subset edos 2, 3, 6, 7, 14, and 21.

Intervals

#	Cents	Ups and downs notation
0	0.0	P1	perfect unison	D
1	28.6	^1, m2	up unison, minor 2nd	^D, Eb
2	57.1	^^1, ^m2	dup 1sn, upminor 2nd	^^D, ^Eb
3	85.7	^^m2	dupminor 2nd	^^Eb
4	114.3	^3m	trupminor 2nd	^3Eb
5	143.9	v3M	trudmajor 2nd	v3E
6	171.4	vvM2	dudmajor 2nd	vvE
7	200.0	vM2	downmajor 2nd	vE
8	228.6	M2	major 2nd	E
9	257.1	m3	minor 3rd	F
10	285.7	^m3	upminor 3rd	^F
11	314.3	^^m3	dupminor 3rd	^^F
12	342.9	^3m3	trupminor 3rd	^3F
13	371.4	v3M3	trudmajor 3rd	v3F#
14	400.0	vvM3	dudmajor 3rd	vvF#
15	428.6	vM3	downmajor 3rd	vF#
16	457.1	M3, v4	major 3rd, down 4th	F#, vG
17	485.7	P4	perfect 4th	G
18	514.3	^4	up 4th	^G
19	543.9	^^4	dup 4th	^^G
20	571.4	^34, ^^d5	trup 4th, dupdim 5th	^3G, ^^Ab
21	600.0	v3A4, ^3d5	trudaug 4th, trupdim 5th	v3G#, ^3Ab
22	628.6	vvA4, v35	dudaug 4th, trud 5th	vvG#, v3A
23	657.1	vv5	dud 5th	vvA
24	685.7	v5	down 5th	vA
25	714.3	P5	perfect 5th	A
26	742.9	^5, m6	up 5th, minor 6th	^A, Bb
27	771.4	^m6	upminor 6th	^Bb
28	800.0	^^m6	dupminor 6th	^^Bb
29	828.6	^3m6	trupminor 6th	^3Bb
30	857.1	v3M6	trudmajor 6th	v3B
31	885.7	vvM6	dudmajor 6th	vvB
32	914.3	vM6	downmajor 6th	vB
33	942.9	M6	major 6th	B
34	971.4	m7	minor 7th	C
35	1000.0	^m7	upminor 7th	^C
36	1028.6	^^m7	dupminor 7th	^^C
37	1057.1	^3m7	trupminor 7th	^3C
38	1085.7	v3M7	trudmajor 7th	v3C#
39	1114.3	vvM7	dudmajor 7th	vvC#
40	1142.9	vM7	downmajor 7th	vC#
41	1171.4	M7, v8	major 7th, down 8ve	C#, vD
42	1200.0	P8	perfect 8ve	D

Chords can be named using ups and downs as C upminor, D downmajor seven, etc. See Ups and downs notation #Chords and chord progressions.

Notation

Ups and downs notation

Assuming the natural notes form a chain of fifths, the major 2nd is 8 edosteps and the minor 2nd is only one. The naturals create a 5edo-like scale, with two of the notes inflected by a comma-sized edostep:

D * * * * * * * E F * * * * * * * G * * * * * * * A * * * * * * * B C * * * * * * * D

D♯ is next to E. The notation requires ups and downs with three arrows, and if chords are to be spelled correctly four or more arrows may be required in certain cases. For example, a 1/1 – 5/4 – 3/2 – 9/5 chord with a root on the edostep midway between G and A would be written either as v³G♯–v⁵B♯ – v³D♯ – vF♯ or as ^³A♭ – ^C – ^³E♭ – ^⁵G♭. This is a dud dup-seven chord, written either as v³G♯vv,^^7 or as ^³A♭vv,^^7.

In this table, dup is equivalent to quidsharp, trup is equivalent to quudsharp, trudsharp is equivalent to quup, dudsharp is equivalent to quip, etc.

Step offset	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Sharp symbol
Flat symbol

Alternatively, sharps and flats with arrows borrowed from Helmholtz–Ellis notation can be used:

Step offset	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Sharp symbol
Flat symbol

Sagittal notation

Best fifth notation

This notation uses the same sagittal sequence as 35b.

Evo flavor

Revo flavor

Second-best fifth notation

This notation uses the same sagittal sequence as 47edo, and is a superset of the notations for edos 21, 14, and 7.

Approximation to JI

The following tables show how 15-odd-limit intervals are represented in 42edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 42edo (direct approximation, even if inconsistent)

Interval and complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
5/3, 6/5	1.356	4.7
15/8, 16/15	2.554	8.9
7/4, 8/7	2.603	9.1
13/10, 20/13	2.929	10.3
13/11, 22/13	3.495	12.2
9/8, 16/9	3.910	13.7
13/12, 24/13	4.284	15.0
11/9, 18/11	4.551	15.9
15/14, 28/15	5.157	18.0
15/11, 22/15	5.906	20.7
11/10, 20/11	6.424	22.5
9/7, 14/9	6.513	22.8
11/6, 12/11	7.780	27.2
13/9, 18/13	8.046	28.2
11/8, 16/11	8.461	29.6
15/13, 26/15	9.402	32.9
7/6, 12/7	9.728	34.0
9/5, 10/9	10.975	38.4
11/7, 14/11	11.063	38.7
7/5, 10/7	11.084	38.8
13/8, 16/13	11.956	41.8
3/2, 4/3	12.331	43.2
5/4, 8/5	13.686	47.9
13/7, 14/13	14.013	49.0

15-odd-limit intervals in 42edo (patent val mapping)

Interval and complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
5/3, 6/5	1.356	4.7
7/4, 8/7	2.603	9.1
13/11, 22/13	3.495	12.2
11/8, 16/11	8.461	29.6
7/6, 12/7	9.728	34.0
9/5, 10/9	10.975	38.4
11/7, 14/11	11.063	38.7
7/5, 10/7	11.084	38.8
13/8, 16/13	11.956	41.8
3/2, 4/3	12.331	43.2
5/4, 8/5	13.686	47.9
13/7, 14/13	14.559	51.0
11/6, 12/11	20.792	72.8
9/7, 14/9	22.059	77.2
11/10, 20/11	22.147	77.5
15/14, 28/15	23.414	82.0
13/12, 24/13	24.287	85.0
9/8, 16/9	24.661	86.3
13/10, 20/13	25.643	89.7
15/8, 16/15	26.017	91.1
11/9, 18/11	33.122	115.9
15/11, 22/15	34.478	120.7
13/9, 18/13	36.618	128.2
15/13, 26/15	37.973	132.9

Regular temperament properties

Subgroup	Comma list	Mapping	Optimal 8ve stretch (¢)	Tuning error
				Absolute (¢)	Relative (%)
2.3	[67 -42⟩	[⟨42 67]]	−3.89	3.88	13.57
2.3.5	128/125, 5000000/4782969	[⟨42 67 98]]	−4.55	3.30	11.55
2.3.5.7	64/63, 126/125, 6860/6561	[⟨42 67 98 118]]	−3.65	3.26	11.42

Octave stretch or compression

42edo’s inaccurate 3rd and 5th harmonics can be greatly improved through stretching or compressing octaves. Both approaches work about equally well but in opposite directions, giving two quite different flavors of tuning to play with.

What follows is a comparison of stretched- and compressed-octave 42edo tunings.

108ed6

• Octave size: 1206.3 ¢

Stretching the octave of 42edo by around 6 ¢ results in improved primes 3, 5 and 13, but worse primes 2, 7 and 11. This approximates all harmonics up to 16 within 13.3 ¢. The tuning 108ed6 does this. So does the tuning 97ed5 whose octave differs by only 0.1 ¢.

Approximation of harmonics in 108ed6

Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+6.3	-6.3	+12.6	-0.3	+0.0	-8.4	-9.8	-12.6	+6.0	+13.3	+6.3
	Relative (%)	+22.0	-22.0	+44.0	-1.0	+0.0	-29.2	-34.0	-44.0	+21.0	+46.5	+22.0
Steps (reduced)		42 (42)	66 (66)	84 (84)	97 (97)	108 (0)	117 (9)	125 (17)	132 (24)	139 (31)	145 (37)	150 (42)

Approximation of harmonics in 108ed6 (continued)

Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	+11.4	-2.1	-6.6	-3.5	+6.5	-6.3	-13.8	+12.3	+14.0	-9.1	+0.1	+12.6
	Relative (%)	+39.5	-7.2	-23.0	-12.0	+22.5	-22.0	-47.9	+42.9	+48.9	-31.6	+0.5	+44.0
Steps (reduced)		155 (47)	159 (51)	163 (55)	167 (59)	171 (63)	174 (66)	177 (69)	181 (73)	184 (76)	186 (78)	189 (81)	192 (84)

189zpi

• Step size: 28.689 ¢, octave size: 1204.9 ¢

Stretching the octave of 42edo by around 5 ¢ results in improved primes 3, 5 and 13, but worse primes 2 and 11. This approximates all harmonics up to 16 within 13.9 ¢. The tuning 189zpi does this.

Approximation of harmonics in 189zpi

Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+4.9	-8.5	+9.9	-3.5	-3.5	-12.2	-13.9	+11.7	+1.5	+8.6	+1.4
	Relative (%)	+17.2	-29.6	+34.4	-12.1	-12.3	-42.6	-48.4	+40.9	+5.1	+29.9	+4.9
Step		42	66	84	97	108	117	125	133	139	145	150

Approximation of harmonics in 189zpi (continued)

Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	+6.3	-7.3	-12.0	-8.9	+0.9	-12.0	+9.1	+6.4	+8.0	+13.5	-6.1	+6.3
	Relative (%)	+21.8	-25.4	-41.7	-31.2	+3.0	-41.9	+31.8	+22.3	+27.9	+47.1	-21.1	+22.1
Step		155	159	163	167	171	174	178	181	184	187	189	192

150ed12

• Octave size: 1204.5 ¢

Stretcing the octave of 42edo by around 4.5 ¢ results in improved primes 3, 5, 11 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 13.6 ¢. The tuning 150ed12 does this.

Approximation of harmonics in 150ed12

Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+4.5	-9.1	+9.1	-4.4	-4.5	-13.3	+13.6	+10.5	+0.2	+7.2	+0.0
	Relative (%)	+15.9	-31.7	+31.7	-15.3	-15.9	-46.4	+47.6	+36.6	+0.6	+25.2	+0.0
Steps (reduced)		42 (42)	66 (66)	84 (84)	97 (97)	108 (108)	117 (117)	126 (126)	133 (133)	139 (139)	145 (145)	150 (0)

Approximation of harmonics in 150ed12 (continued)

Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	+4.8	-8.8	-13.5	-10.5	-0.7	-13.6	+7.5	+4.7	+6.3	+11.8	-7.8	+4.5
	Relative (%)	+16.8	-30.5	-47.0	-36.6	-2.5	-47.6	+26.1	+16.4	+21.9	+41.1	-27.2	+15.9
Steps (reduced)		155 (5)	159 (9)	163 (13)	167 (17)	171 (21)	174 (24)	178 (28)	181 (31)	184 (34)	187 (37)	189 (39)	192 (42)

145ed11

• Octave size: 1202.5 ¢

Stretching the octave of 42edo by around 2.5 ¢ results in improved primes 5, 11 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 11.9 ¢. The tuning 145ed11 does this.

Approximation of harmonics in 145ed11

Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+2.5	-12.4	+4.9	-9.2	-9.9	+9.5	+7.4	+3.9	-6.8	+0.0	-7.5
	Relative (%)	+8.6	-43.3	+17.1	-32.2	-34.7	+33.1	+25.7	+13.4	-23.7	+0.0	-26.2
Steps (reduced)		42 (42)	66 (66)	84 (84)	97 (97)	108 (108)	118 (118)	126 (126)	133 (133)	139 (139)	145 (0)	150 (5)

Approximation of harmonics in 145ed11 (continued)

Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-2.9	+11.9	+7.0	+9.8	-9.3	+6.3	-1.4	-4.3	-2.9	+2.5	+11.4	-5.0
	Relative (%)	-10.2	+41.7	+24.5	+34.2	-32.4	+22.0	-4.9	-15.1	-10.1	+8.6	+39.8	-17.6
Steps (reduced)		155 (10)	160 (15)	164 (19)	168 (23)	171 (26)	175 (30)	178 (33)	181 (36)	184 (39)	187 (42)	190 (45)	192 (47)

42edo

• Step size: 28.571 ¢, octave size: 1200.0 ¢

Pure-octaves 42edo approximates all harmonics up to 16 within 13.7 ¢. The tuning 190zpi is almost exactly the same as pure-octaves 42edo, its octave differing by less than 0.05 ¢.

Approximation of harmonics in 42edo

Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	+0.0	+12.3	+0.0	+13.7	+12.3	+2.6	+0.0	-3.9	+13.7	-8.5	+12.3
	Relative (%)	+0.0	+43.2	+0.0	+47.9	+43.2	+9.1	+0.0	-13.7	+47.9	-29.6	+43.2
Steps (reduced)		42 (0)	67 (25)	84 (0)	98 (14)	109 (25)	118 (34)	126 (0)	133 (7)	140 (14)	145 (19)	151 (25)

Approximation of harmonics in 42edo (continued)

Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-12.0	+2.6	-2.6	+0.0	+9.3	-3.9	-11.8	+13.7	-13.6	-8.5	+0.3	+12.3
	Relative (%)	-41.8	+9.1	-8.9	+0.0	+32.7	-13.7	-41.3	+47.9	-47.7	-29.6	+1.0	+43.2
Steps (reduced)		155 (29)	160 (34)	164 (38)	168 (0)	172 (4)	175 (7)	178 (10)	182 (14)	184 (16)	187 (19)	190 (22)	193 (25)

118ed7

• Step size: Octave size: 1199.1 ¢

Compressing the octave of 42edo by around 1 ¢ results in improved primes 3, 5 and 7, but worse primes 2, 11 and 13. This approximates all harmonics up to 16 within 13.2 ¢. The tuning 118ed7 does this.

Approximation of harmonics in 118ed7

Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	-0.9	+10.9	-1.9	+11.5	+9.9	+0.0	-2.8	-6.8	+10.6	-11.7	+9.0
	Relative (%)	-3.2	+38.0	-6.5	+40.4	+34.8	+0.0	-9.7	-24.0	+37.1	-40.8	+31.5
Steps (reduced)		42 (42)	67 (67)	84 (84)	98 (98)	109 (109)	118 (0)	126 (8)	133 (15)	140 (22)	145 (27)	151 (33)

Approximation of harmonics in 118ed7 (continued)

Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	+13.2	-0.9	-6.2	-3.7	+5.5	-7.8	+12.8	+9.7	+10.9	-12.6	-3.9	+8.1
	Relative (%)	+46.1	-3.2	-21.6	-13.0	+19.4	-27.2	+44.9	+33.9	+38.0	-44.1	-13.6	+28.3
Steps (reduced)		156 (38)	160 (42)	164 (46)	168 (50)	172 (54)	175 (57)	179 (61)	182 (64)	185 (67)	187 (69)	190 (72)	193 (75)

42et, 13-limit WE tuning

• Step size: 28.534 ¢, octave size: 1198.4 ¢

Compressing the octave of 42edo by around 1.5 ¢ results in improved primes 3, 5, 7 and 13, but worse primes 2 and 11. This approximates all harmonics up to 16 within 13.9 ¢. Its 13-limit WE tuning and 13-limit TE tuning both do this.

Of the tunings discussed in this section, 13-limit WE and TE are the only ones to approximate all harmonics up to 10 within 10 cents, making them a good all-round choice.

Approximation of harmonics in 42et, 13-limit WE tuning

Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	-1.6	+9.8	-3.1	+10.0	+8.3	-1.8	-4.7	-8.9	+8.4	-13.9	+6.7
	Relative (%)	-5.5	+34.4	-11.0	+35.1	+28.9	-6.4	-16.5	-31.1	+29.6	-48.7	+23.4
Step		42	67	84	98	109	118	126	133	140	145	151

Approximation of harmonics in 42et, 13-limit WE tuning (continued)

Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	+10.8	-3.4	-8.7	-6.3	+2.9	-10.5	+10.1	+6.9	+8.0	+13.1	-6.8	+5.1
	Relative (%)	+37.8	-11.9	-30.5	-22.0	+10.1	-36.7	+35.3	+24.1	+28.1	+45.8	-23.9	+17.9
Step		156	160	164	168	172	175	179	182	185	188	190	193

151ed12

• Step size: Octave size: 1196.6 ¢

Compressing the octave of 42edo by around 3.5 ¢ results in improved primes 3, 5, 11 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 13.7 ¢. The tuning 151ed12 does this. So do the 7-limit WE and TE tunings of 42et, whose octaves are within 0.3 ¢ of 151ed12.

Approximation of harmonics in 151ed12

Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	-3.4	+6.9	-6.9	+5.7	+3.4	-7.0	-10.3	+13.7	+2.3	+8.2	+0.0
	Relative (%)	-12.0	+24.1	-24.1	+19.9	+12.0	-24.7	-36.1	+48.2	+7.9	+28.7	+0.0
Steps (reduced)		42 (42)	67 (67)	84 (84)	98 (98)	109 (109)	118 (118)	126 (126)	134 (134)	140 (140)	146 (146)	151 (0)

Approximation of harmonics in 151ed12 (continued)

Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	+3.9	-10.5	+12.5	-13.7	-4.7	+10.3	+2.2	-1.2	-0.2	+4.8	+13.3	-3.4
	Relative (%)	+13.6	-36.7	+44.0	-48.2	-16.6	+36.1	+7.6	-4.1	-0.6	+16.7	+46.6	-12.0
Steps (reduced)		156 (5)	160 (9)	165 (14)	168 (17)	172 (21)	176 (25)	179 (28)	182 (31)	185 (34)	188 (37)	191 (40)	193 (42)

109ed6

• Octave size: 1195.2 ¢

Compressing the octave of 42edo by around 5 ¢ results in improved primes 3, 5, 11 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 14.2 ¢. The tuning 109ed6 does this.

Approximation of harmonics in 109ed6

Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	-4.8	+4.8	-9.5	+2.6	+0.0	-10.7	+14.2	+9.5	-2.2	+3.6	-4.8
	Relative (%)	-16.7	+16.7	-33.4	+9.1	+0.0	-37.8	+49.9	+33.4	-7.6	+12.6	-16.7
Steps (reduced)		42 (42)	67 (67)	84 (84)	98 (98)	109 (0)	118 (9)	127 (18)	134 (25)	140 (31)	146 (37)	151 (42)

Approximation of harmonics in 109ed6 (continued)

Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-1.0	+13.0	+7.4	+9.5	-10.1	+4.8	-3.5	-6.9	-6.0	-1.2	+7.3	-9.5
	Relative (%)	-3.6	+45.5	+25.8	+33.2	-35.6	+16.7	-12.2	-24.3	-21.1	-4.1	+25.5	-33.4
Steps (reduced)		156 (47)	161 (52)	165 (56)	169 (60)	172 (63)	176 (67)	179 (70)	182 (73)	185 (76)	188 (79)	191 (82)	193 (84)

191zpi

• Step size: 28.444 ¢, octave size: 1194.6 ¢

Compressing the octave of 42edo by around 5.5 ¢ results in improved primes 3, 5, 11 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 12.4 ¢. The tuning 191zpi does this.

Approximation of harmonics in 191zpi

Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	-5.4	+3.8	-10.7	+1.2	-1.6	-12.4	+12.4	+7.6	-4.2	+1.5	-6.9
	Relative (%)	-18.8	+13.3	-37.6	+4.2	-5.5	-43.7	+43.6	+26.7	-14.6	+5.3	-24.3
Step		42	67	84	98	109	118	127	134	140	146	151

Approximation of harmonics in 191zpi (continued)

Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-3.3	+10.7	+5.0	+7.0	-12.6	+2.2	-6.0	-9.5	-8.6	-3.8	+4.5	-12.3
	Relative (%)	-11.5	+37.5	+17.5	+24.7	-44.3	+7.9	-21.2	-33.4	-30.4	-13.5	+15.9	-43.1
Step		156	161	165	169	172	176	179	182	185	188	191	193

67edt

• Step size: 28.387 ¢, octave size: 1192.3 ¢

Compressing the octave of 42edo by around 7.5 ¢ results in improved primes 3, 5 and 11, but worse primes 2 and 7. This approximates all harmonics up to 16 within 12.9 ¢. The tuning 67edt does this.

Approximation of harmonics in 67edt

Harmonic		2	3	4	5	6	7	8	9	10	11	12
Error	Absolute (¢)	-7.7	+0.0	+12.9	-4.3	-7.7	+9.3	+5.2	+0.0	-12.1	-6.8	+12.9
	Relative (%)	-27.2	+0.0	+45.5	-15.3	-27.2	+32.7	+18.3	+0.0	-42.6	-23.8	+45.5
Steps (reduced)		42 (42)	67 (0)	85 (18)	98 (31)	109 (42)	119 (52)	127 (60)	134 (0)	140 (6)	146 (12)	152 (18)

Approximation of harmonics in 67edt (continued)

Harmonic		13	14	15	16	17	18	19	20	21	22	23	24
Error	Absolute (¢)	-12.1	+1.5	-4.3	-2.5	+6.1	-7.7	+12.2	+8.6	+9.3	+13.9	-6.3	+5.2
	Relative (%)	-42.6	+5.4	-15.3	-8.9	+21.4	-27.2	+43.0	+30.2	+32.7	+49.0	-22.1	+18.3
Steps (reduced)		156 (22)	161 (27)	165 (31)	169 (35)	173 (39)	176 (42)	180 (46)	183 (49)	186 (52)	189 (55)	191 (57)	194 (60)

Scales

Main article: List of MOS scales in 42edo

MOS scales

• Eugene/Tritikleismic[9]: 3 8 3 3 8 3 3 8 3
• Eugene/Tritikleismic[15]: 3 3 2 3 3 3 3 2 3 3 3 3 2 3 3
• Lemba[16]: 3 2 3 2 3 3 2 3 3 2 3 2 3 3 2 3
• Qeema/Skateboard[15]: 2 5 2 2 2 5 2 2 2 5 2 2 2 5 2
• Qeema/Skateboard[19]: 2 2 3 2 2 2 2 3 2 2 2 3 2 2 2 2 3 2 2
• Seville/Sevond[14] 1st mode: 1 5 1 5 1 5 1 5 1 5 1 5 1 5
• Seville/Sevond[14] 2nd mode: 5 1 5 1 5 1 5 1 5 1 5 1 5 1
• Seville/Sevond[21]: 1 4 1 1 4 1 1 4 1 1 4 1 1 4 1 1 4 1 1 4

Subsets of MOS scales

(Names used are idiosyncratic.)

• Eugene/Tritikleismic[9]
  • Groovy aeolian pentatonic: 11 6 8 3 14
  • Otonal mixolydian pentatonic: 14 3 8 11 6
  • Pseudo-equipentatonic: 11 6 8 6 11
  • Septimal melodic minor pentatonic: 8 3 14 14 3
  • Septimal Picardy pentatonic: 8 6 11 3 14
  • Undecimal lydian-aeolian pentatonic: 8 14 3 11 6
  • Yokai pentatonic: 3 14 8 3 14

Approximations of gamelan scales

• 5-tone pelog: 4 5 15 3 15
• 7-tone pelog: 4 5 9 6 3 10 5
• 5-tone slendro: 8 9 8 9 8

Instruments

Lumatone

Main article: Lumatone mapping for 42edo

Skip fretting

Skip fretting system 42 3 11: One way to play 42edo on a 14edo guitar is to tune the strings 11\42, or approximately a just 6/5, apart. All examples on this page are for 7-string guitar.

Prime intervals

1/1: string 2 open

2/1: string 5 fret 3

3/2: string 4 fret 1 and string 7 fret 4

5/4: string 3 fret 1

7/4: string 1 fret 1 and string 4 fret 4

11/8: string 7 fret 2

13/8: string 3 fret 6

17/16: string 1 fret 5

19/16: string 1 fret 7

23/16: string 4 open and string 7 fret 3

29/16: string 5 fret 1

31/16: string 1 fret 3 and string 4 fret 6

Chords

Minor 7th: 100123X

Music

Modern renderings

Johann Sebastian Bach

• "Ricercar a 3" from The Musical Offering, BWV 1079 (1747) – rendered by Claudi Meneghin (2024)

Bing Crosby

• White Christmas - 42edo reimagining by Todd Harrop (2024)

21st century

Bryan Deister

• improv 42edo (2023)
• Improvisation in 42edo (2023), transcribed by Stephen Weigel (2024)

James Kukula

• Circulating and Traversing (2024) - see the composer’s notes

Budjarn Lambeth

• Four Short Experiments in Octave Stretched 42edo (2024)

Herman Miller

• Through the Dark (2024) - uses mostly Augene[15] with some chromaticism

Mundoworld

• Glory of Them (2024)