71zpi

71 zeta peak index (abbreviated 71zpi), is the equal-step tuning system obtained from the 71st peak of the Riemann zeta function.

Tuning			Strength			Closest EDO		Integer limit
ZPI	Steps per octave	Step size (cents)	Height	Integral	Gap	EDO	Octave (cents)	Consistent	Distinct
71zpi	20.2248393119540	59.3329806724710	3.531097	0.613581	12.986080	20edo	1186.65961344942	6	6

The Riemann zeta function around 71zpi

Theory

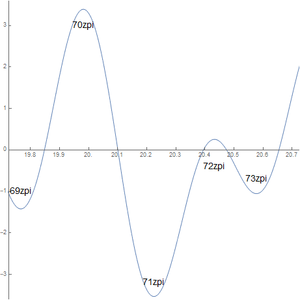
71zpi marks the most prominent zeta peak index in the vicinity of 20edo. While 70zpi is the nearest peak to 20edo and closely competes with 71zpi in terms of strength, 71zpi remains superior across all measures of strength. 71zpi may also be viewed as a tritave compression of 32edt, a no-2s zeta peak EDT (consistent in the no-2s 21-throdd-limit), but with less extreme stretch than the no-2s peak at 59.271105 cents.

71zpi features a good 3:5:9:11:14:15:16:19:25:26:33 chord, which differs a lot from the harmonic characteristics of 20edo.

The nearest zeta peaks to 71zpi that surpass its strength are 65zpi and 75zpi.

71zpi is distinguished by its extensive EDO-deviation and substantial zeta strength, qualifying it as a strong candidate for no-octave tuning systems. It is noteworthy that only 19zpi exhibits both a greater octave error and stronger zeta height and integral than 71zpi, although 71zpi still has a more pronounced zeta gap. Other notable zeta peak indices in this category include 61zpi, 84zpi, 110zpi, 137zpi, 151zpi, 222zpi, and 273zpi, each demonstrating characteristics that make them suitable for similar applications.

Harmonic series

Approximation of harmonics in 71zpi

Harmonic		2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Error	Absolute (¢)	-13.3	-3.3	-26.7	+2.3	-16.6	+13.2	+19.3	-6.6	-11.0	+2.0	+29.4	+9.4	-0.2	-1.0	+6.0
	Relative (%)	-22.5	-5.6	-45.0	+3.9	-28.0	+22.2	+32.5	-11.1	-18.5	+3.4	+49.5	+15.9	-0.3	-1.6	+10.1
Step		20	32	40	47	52	57	61	64	67	70	73	75	77	79	81

Approximation of harmonics in 71zpi

Harmonic		17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33
Error	Absolute (¢)	+19.7	-19.9	+5.1	-24.3	+9.9	-11.3	-29.0	+16.0	+4.7	-3.9	-9.9	-13.5	-14.9	-14.3	-11.7	-7.4	-1.3
	Relative (%)	+33.2	-33.6	+8.6	-41.0	+16.6	-19.1	-48.8	+27.0	+7.9	-6.6	-16.7	-22.8	-25.2	-24.1	-19.8	-12.4	-2.2
Step		83	84	86	87	89	90	91	93	94	95	96	97	98	99	100	101	102

Intervals

There are multiple ways to approach notation. The simplest method is to use the notations from 20edo. However, this approach will not preserve octave compression when the audio is rendered by notation software. If maintaining accurate step compression in notation software is important, consider using the ups and downs notation from 182edo at every 9-degree step. With this method, the tonal difference will be less than 1 cent up to the 86th harmonic.

Intervals in 71zpi

JI ratios are comprised of 32-integer limit ratios, and are stylized as follows to indicate their accuracy: Bold Underlined: relative error < 8.333 % Bold: relative error < 16.667 % Normal: relative error < 25 % Small: relative error < 33.333 % Small Small: relative error < 41.667 % Small Small Small: relative error < 50 %			⟨182 288] at every 9 steps Whole tone = 30 steps Limma = 16 steps Apotome = 14 steps
Degree	Cents	Ratios	Ups and Downs Notation	Step
0	0.000		P1	0
1	59.333	32/31, 31/30, 30/29, 29/28, 28/27, 27/26, 26/25, 25/24, 24/23, 23/22, 22/21, 21/20, 20/19	v7m2	9
2	118.666	19/18, 18/17, 17/16, 16/15, 31/29, 15/14, 29/27, 14/13, 27/25, 13/12, 25/23	^^m2	18
3	177.999	12/11, 23/21, 11/10, 32/29, 21/19, 31/28, 10/9, 29/26, 19/17, 28/25, 9/8	vvvM2	27
4	237.332	26/23, 17/15, 25/22, 8/7, 31/27, 23/20, 15/13, 22/19, 29/25, 7/6	^6M2	36
5	296.665	27/23, 20/17, 13/11, 32/27, 19/16, 25/21, 31/26, 6/5	vm3	45
6	355.998	29/24, 23/19, 17/14, 28/23, 11/9, 27/22, 16/13, 21/17, 26/21, 31/25	v6M3	54
7	415.331	5/4, 29/23, 24/19, 19/15, 14/11, 23/18, 32/25, 9/7, 31/24	^^^M3	63
8	474.664	22/17, 13/10, 30/23, 17/13, 21/16, 25/19, 29/22, 4/3	v44	72
9	533.997	31/23, 27/20, 23/17, 19/14, 15/11, 26/19, 11/8, 29/21, 18/13	^54	81
10	593.330	25/18, 32/23, 7/5, 31/22, 24/17, 17/12, 27/19, 10/7	A4	90
11	652.663	23/16, 13/9, 29/20, 16/11, 19/13, 22/15, 25/17, 28/19, 31/21	~5	99
12	711.996	3/2, 32/21, 29/19, 26/17, 23/15	^^5	108
13	771.329	20/13, 17/11, 31/20, 14/9, 25/16, 11/7, 30/19, 19/12, 27/17	v5m6	117
14	830.662	8/5, 29/18, 21/13, 13/8, 31/19, 18/11, 23/14	^4m6	126
15	889.995	28/17, 5/3, 32/19, 27/16, 22/13, 17/10	vM6	135
16	949.328	29/17, 12/7, 31/18, 19/11, 26/15, 7/4	v6A6, ^6d7	144
17	1008.661	30/17, 23/13, 16/9, 25/14, 9/5, 29/16, 20/11	^m7	153
18	1067.994	31/17, 11/6, 24/13, 13/7, 28/15, 15/8, 32/17	v4M7	162
19	1127.327	17/9, 19/10, 21/11, 23/12, 25/13, 27/14, 29/15, 31/16	^5M7	171
20	1186.660	2/1	vv1 +1 oct	180
21	1245.993	31/15, 29/14, 27/13, 25/12	^71 +1 oct	189
22	1305.326	23/11, 21/10, 19/9, 17/8, 32/15, 15/7, 28/13	m2 +1 oct	198
23	1364.659	13/6, 24/11, 11/5, 31/14, 20/9, 29/13	v5M2 +1 oct	207
24	1423.992	9/4, 25/11, 16/7, 23/10, 30/13	^4M2 +1 oct	216
25	1483.325	7/3, 26/11, 19/8, 31/13	vvvm3 +1 oct	225
26	1542.657	12/5, 29/12, 17/7, 22/9, 27/11, 32/13	^6m3 +1 oct	234
27	1601.990	5/2, 28/11, 23/9	^M3 +1 oct	243
28	1661.323	18/7, 31/12, 13/5, 21/8, 29/11	v64 +1 oct	252
29	1720.656	8/3, 27/10, 19/7, 30/11	^^^4 +1 oct	261
30	1779.989	11/4, 25/9, 14/5, 31/11, 17/6	vvA4 +1 oct	270
31	1839.322	20/7, 23/8, 26/9, 29/10, 32/11	^5d5 +1 oct	279
32	1898.655	3/1	P5 +1 oct	288
33	1957.988	31/10, 28/9, 25/8, 22/7	v7m6 +1 oct	297
34	2017.321	19/6, 16/5, 29/9, 13/4	^^m6 +1 oct	306
35	2076.654	23/7, 10/3, 27/8	vvvM6 +1 oct	315
36	2135.987	17/5, 24/7, 31/9	^6M6 +1 oct	324
37	2195.320	7/2, 32/9, 25/7, 18/5	vm7 +1 oct	333
38	2254.653	29/8, 11/3, 26/7	v6M7 +1 oct	342
39	2313.986	15/4, 19/5, 23/6, 27/7	^^^M7 +1 oct	351
40	2373.319	31/8, 4/1	v41 +2 oct	360
41	2432.652	29/7	^51 +2 oct	369
42	2491.985	25/6, 21/5, 17/4, 30/7	vvm2 +2 oct	378
43	2551.318	13/3, 22/5, 31/7	~2 +2 oct	387
44	2610.651	9/2, 32/7	^^M2 +2 oct	396
45	2669.984	23/5, 14/3, 19/4	v5m3 +2 oct	405
46	2729.317	24/5, 29/6	^4m3 +2 oct	414
47	2788.650	5/1	vM3 +2 oct	423
48	2847.983	31/6, 26/5, 21/4	v6A3 +2 oct, ^6d4 +2 oct	432
49	2907.316	16/3, 27/5	^4 +2 oct	441
50	2966.649	11/2, 28/5	v4A4 +2 oct	450
51	3025.982	17/3, 23/4, 29/5	^^^d5 +2 oct	459
52	3085.315	6/1	vv5 +2 oct	468
53	3144.648	31/5, 25/4	^75 +2 oct	477
54	3203.981	19/3, 32/5	m6 +2 oct	486
55	3263.314	13/2, 20/3	v5M6 +2 oct	495
56	3322.647	27/4	^4M6 +2 oct	504
57	3381.980	7/1	vvvm7 +2 oct	513
58	3441.313	29/4, 22/3	^6m7 +2 oct	522
59	3500.646	15/2, 23/3	^M7 +2 oct	531
60	3559.979	31/4	v61 +3 oct	540
61	3619.312	8/1	^^^1 +3 oct	549
62	3678.645	25/3, 17/2	v4m2 +3 oct	558
63	3737.978	26/3	^5m2 +3 oct	567
64	3797.311	9/1	M2 +3 oct	576
65	3856.644	28/3	v7m3 +3 oct	585
66	3915.977	19/2, 29/3	^^m3 +3 oct	594
67	3975.310	10/1	vvvM3 +3 oct	603
68	4034.643	31/3	^6M3 +3 oct	612
69	4093.976	21/2, 32/3	v4 +3 oct	621
70	4153.309	11/1	v6A4 +3 oct	630
71	4212.642	23/2	^d5 +3 oct	639
72	4271.975		v45 +3 oct	648
73	4331.308	12/1	^55 +3 oct	657
74	4390.641	25/2	vvm6 +3 oct	666
75	4449.974	13/1	~6 +3 oct	675
76	4509.307	27/2	^^M6 +3 oct	684
77	4568.640	14/1	v5m7 +3 oct	693
78	4627.972	29/2	^4m7 +3 oct	702
79	4687.305	15/1	vM7 +3 oct	711
80	4746.638	31/2	v6A7 +3 oct, ^6d1 +4 oct	720
81	4805.971	16/1	^1 +4 oct	729
82	4865.304		v6m2 +4 oct	738
83	4924.637	17/1	^^^m2 +4 oct	747
84	4983.970	18/1	vvM2 +4 oct	756
85	5043.303		^7M2 +4 oct	765
86	5102.636	19/1	m3 +4 oct	774
87	5161.969	20/1	v5M3 +4 oct	783
88	5221.302		^4M3 +4 oct	792
89	5280.635	21/1	vvv4 +4 oct	801
90	5339.968	22/1	^64 +4 oct	810
91	5399.301	23/1	^A4 +4 oct, vd5 +4 oct	819
92	5458.634		v65 +4 oct	828
93	5517.967	24/1	^^^5 +4 oct	837
94	5577.300	25/1	v4m6 +4 oct	846
95	5636.633	26/1	^5m6 +4 oct	855
96	5695.966	27/1	M6 +4 oct	864
97	5755.299	28/1	v7m7 +4 oct	873
98	5814.632	29/1	^^m7 +4 oct	882
99	5873.965	30/1	vvvM7 +4 oct	891
100	5933.298	31/1	^6M7 +4 oct	900
101	5992.631	32/1	v1 +5 oct	909

Approximation to JI

The following table illustrates the representation of the 32-integer limit intervals in 71zpi. Prime harmonics are in bold; inconsistent intervals are in italic.

Intervals by direct approximation (even if inconsistent)

Ratio	Error (abs, ¢)	Error (rel, %)
14/1	+0.186	+0.314
11/5	+0.346	+0.583
17/8	-0.370	-0.624
31/22	+0.388	+0.654
21/13	-0.408	-0.688
25/19	+0.451	+0.759
26/3	+0.595	+1.003
30/29	-0.641	-1.081
31/10	+0.733	+1.236
32/9	+0.770	+1.297
15/14	+0.777	+1.309
19/16	+0.848	+1.429
15/1	+0.963	+1.623
23/12	-1.007	-1.698
27/10	-1.105	-1.863
25/16	+1.299	+2.189
29/28	+1.418	+2.390
27/22	-1.451	-2.445
31/2	-1.603	-2.702
29/2	+1.605	+2.705
29/6	-1.695	-2.857
31/28	-1.789	-3.016
31/27	+1.839	+3.099
11/1	-1.991	-3.355
14/11	+2.177	+3.669
23/4	+2.292	+3.864
5/1	-2.336	-3.938
14/5	+2.523	+4.252
32/27	-2.530	-4.264
31/30	-2.566	-4.325
25/11	-2.682	-4.520
26/9	-2.705	-4.559
19/5	-2.787	-4.697
24/7	-2.858	-4.817
26/15	+2.931	+4.940
15/11	+2.954	+4.979
14/3	-3.113	-5.247
19/11	-3.133	-5.280
31/29	-3.208	-5.406
3/1	+3.300	+5.561
27/2	-3.442	-5.800
16/13	+3.474	+5.856
29/22	+3.595	+6.060
28/27	+3.628	+6.115
16/5	-3.635	-6.127
24/17	+3.670	+6.185
13/7	+3.708	+6.250
21/16	-3.883	-6.544
26/1	+3.894	+6.564
29/10	+3.941	+6.642
16/11	-3.981	-6.709
32/3	+4.069	+6.858
19/13	+4.323	+7.285
32/31	-4.369	-7.363
10/9	+4.405	+7.424
23/20	+4.629	+7.801
25/1	-4.673	-7.875
21/19	-4.731	-7.974
22/9	+4.750	+8.006
25/13	+4.773	+8.045
25/14	-4.859	-8.190
31/6	-4.903	-8.263
29/18	-4.995	-8.418
29/27	+5.046	+8.505
19/1	-5.123	-8.635
31/9	+5.138	+8.660
25/21	+5.182	+8.733
11/3	-5.290	-8.916
19/14	-5.310	-8.949
5/3	-5.636	-9.499
26/11	+5.885	+9.919
16/1	-5.971	-10.064
27/26	+6.004	+10.120
19/15	-6.087	-10.258
8/7	-6.158	-10.378
26/5	+6.231	+10.502
32/15	+6.406	+10.796
14/9	-6.413	-10.808
17/7	-6.528	-11.002
24/13	-6.566	-11.067
9/1	+6.599	+11.122
9/2	-6.741	-11.362
28/9	+6.928	+11.676
16/15	-6.935	-11.688
13/5	-7.110	-11.982
16/7	+7.183	+12.106
32/1	+7.369	+12.420
13/11	-7.455	-12.565
21/5	-7.518	-12.671
32/29	-7.576	-12.769
10/3	+7.704	+12.985
31/26	+7.843	+13.219
21/11	-7.864	-13.253
25/3	-7.972	-13.437
19/7	+8.031	+13.535
22/3	+8.050	+13.568
31/18	-8.202	-13.824
29/9	+8.346	+14.066
19/3	-8.423	-14.196
31/3	+8.438	+14.221
25/7	+8.481	+14.294
26/25	+8.567	+14.439
11/9	-8.590	-14.478
9/5	+8.936	+15.060
26/19	+9.018	+15.199
23/18	+9.033	+15.225
16/3	-9.271	-15.625
32/11	+9.360	+15.775
29/20	-9.399	-15.842
13/1	-9.446	-15.920
21/8	+9.457	+15.940
14/13	+9.632	+16.234
17/12	+9.671	+16.299
32/5	+9.705	+16.357
27/14	+9.712	+16.369
21/17	+9.828	+16.563
21/1	-9.854	-16.609
13/8	+9.866	+16.628
27/1	+9.899	+16.684
3/2	-10.041	-16.923
28/3	+10.227	+17.237
17/13	-10.236	-17.252
22/15	+10.386	+17.505
15/13	+10.409	+17.544
23/17	-10.678	-17.997
31/15	+10.774	+18.159
7/5	-10.818	-18.232
24/19	-10.889	-18.352
10/1	+11.004	+18.546
23/8	-11.048	-18.620
29/26	+11.051	+18.625
11/7	+11.163	+18.815
25/9	-11.272	-18.998
25/24	+11.339	+19.112
22/1	+11.350	+19.129
31/14	+11.551	+19.468
29/3	+11.645	+19.627
19/9	-11.723	-19.757
29/4	-11.736	-19.779
31/1	+11.738	+19.782
27/11	+11.890	+20.039
32/25	+12.042	+20.295
27/5	+12.235	+20.621
23/6	+12.333	+20.786
15/2	-12.377	-20.860
32/19	+12.492	+21.055
28/15	+12.564	+21.175
16/9	-12.571	-21.187
31/20	-12.607	-21.248
13/3	-12.746	-21.481
17/4	+12.970	+21.860
11/10	-12.995	-21.901
7/1	-13.154	-22.170
2/1	+13.340	+22.484
28/1	+13.527	+22.798
24/5	-13.676	-23.049
22/5	+13.686	+23.067
17/16	-13.711	-23.108
31/11	+13.728	+23.138
26/21	+13.749	+23.172
29/15	+13.982	+23.565
24/11	-14.021	-23.632
29/23	-14.028	-23.643
31/5	+14.074	+23.720
15/7	+14.117	+23.793
19/8	+14.188	+23.913
30/1	+14.304	+24.107
24/23	+14.348	+24.182
27/20	-14.446	-24.347
19/17	+14.559	+24.537
27/25	+14.572	+24.559
25/8	+14.639	+24.673
30/23	-14.669	-24.724
29/14	+14.759	+24.874
31/4	-14.943	-25.185
29/1	+14.945	+25.189
25/17	+15.009	+25.297
27/19	+15.022	+25.318
29/12	-15.035	-25.341
20/17	-15.307	-25.798
11/2	-15.331	-25.839
28/23	-15.446	-26.033
28/11	+15.517	+26.153
23/2	+15.633	+26.347
5/2	-15.677	-26.422
28/5	+15.863	+26.736
27/16	+15.870	+26.748
24/1	-16.012	-26.987
25/22	-16.022	-27.004
13/9	-16.045	-27.043
19/10	-16.127	-27.181
12/7	-16.199	-27.301
30/11	+16.294	+27.463
31/25	+16.410	+27.658
7/3	-16.454	-27.731
22/19	+16.473	+27.764
6/1	+16.640	+28.045
27/4	-16.782	-28.284
32/13	+16.815	+28.340
31/19	+16.861	+28.417
29/11	+16.936	+28.544
8/5	-16.975	-28.610
26/7	+17.048	+28.734
23/7	-17.206	-28.999
32/21	+17.223	+29.028
31/23	-17.236	-29.049
29/5	+17.281	+29.126
11/8	+17.321	+29.193
17/5	-17.346	-29.234
23/22	+17.623	+29.703
17/11	-17.691	-29.817
31/16	+17.709	+29.847
20/9	+17.745	+29.908
23/10	+17.969	+30.285
25/2	-18.013	-30.359
28/25	+18.200	+30.674
31/12	-18.243	-30.747
19/2	-18.464	-31.119
11/6	-18.631	-31.400
28/19	+18.650	+31.433
6/5	+18.976	+31.983
27/23	-19.074	-32.148
8/1	-19.312	-32.548
27/13	+19.345	+32.604
30/19	+19.427	+32.742
7/4	+19.498	+32.862
29/25	+19.618	+33.064
17/1	-19.682	-33.172
18/17	-19.711	-33.222
9/7	+19.753	+33.292
17/14	-19.868	-33.486
13/12	+19.907	+33.551
18/1	+19.940	+33.606
29/19	+20.068	+33.823
9/4	-20.082	-33.845
15/8	+20.275	+34.172
13/10	-20.450	-34.466
23/21	-20.506	-34.560
32/7	+20.523	+34.589
17/15	-20.645	-34.796
22/13	+20.796	+35.049
21/10	-20.858	-35.155
23/13	-20.914	-35.249
29/16	+20.917	+35.253
20/3	+21.045	+35.469
31/13	+21.183	+35.703
22/21	+21.204	+35.737
25/6	-21.313	-35.921
31/21	+21.592	+36.391
32/23	-21.604	-36.412
19/6	-21.763	-36.680
20/7	-21.835	-36.800
18/11	+21.930	+36.961
18/5	+22.276	+37.544
23/9	+22.374	+37.709
8/3	-22.611	-38.109
13/2	-22.786	-38.404
21/4	+22.798	+38.424
28/13	+22.973	+38.718
17/3	-22.982	-38.733
17/6	+23.011	+38.783
27/7	+23.053	+38.853
21/2	-23.195	-39.093
13/4	+23.206	+39.112
4/3	+23.381	+39.407
26/17	+23.576	+39.736
30/13	+23.750	+40.028
10/7	+24.158	+40.716
19/12	+24.229	+40.836
20/1	+24.344	+41.030
23/16	-24.388	-41.104
29/13	+24.391	+41.109
22/7	+24.504	+41.299
25/18	-24.612	-41.482
25/12	+24.680	+41.595
29/17	-24.706	-41.639
29/21	+24.799	+41.797
31/7	+24.891	+41.952
19/18	-25.063	-42.241
29/8	-25.076	-42.263
26/23	-25.079	-42.268
21/20	+25.134	+42.361
23/19	-25.237	-42.534
30/17	-25.347	-42.721
20/13	-25.543	-43.050
23/3	+25.673	+43.270
25/23	+25.687	+43.293
15/4	-25.718	-43.344
9/8	+25.911	+43.671
13/6	-26.086	-43.965
28/17	-26.124	-44.030
18/7	-26.239	-44.224
17/9	-26.281	-44.294
17/2	+26.311	+44.344
20/11	+26.335	+44.385
7/2	-26.494	-44.654
4/1	+26.681	+44.968
12/5	-27.016	-45.533
32/17	+27.051	+45.592
12/11	-27.362	-46.116
30/7	+27.458	+46.277
19/4	+27.529	+46.397
31/24	+27.750	+46.769
31/17	-27.913	-47.045
25/4	+27.979	+47.157
23/15	+28.010	+47.208
23/5	-28.023	-47.231
29/7	+28.099	+47.358
31/8	-28.284	-47.669
22/17	-28.301	-47.699
23/11	-28.369	-47.813
29/24	-28.376	-47.824
17/10	+28.647	+48.282
11/4	-28.671	-48.323
23/14	+28.787	+48.517
23/1	+28.973	+48.831
5/4	-29.017	-48.906
27/8	+29.211	+49.232
12/1	-29.353	-49.471
18/13	+29.386	+49.526
20/19	+29.468	+49.665
7/6	+29.539	+49.785
27/17	+29.581	+49.856

Record on the Riemann zeta function with prime 2 removed

71zpi sets a height record on the Riemann zeta function with prime 2 removed. The previous record is 53zpi and the next one is 93zpi. It is important to highlight that the optimal equal tunings obtained by excluding the prime numbers 2 from the Riemann zeta function differs slightly from the optimal equal tuning corresponding to the same peaks on the unmodified Riemann zeta function.

Unmodified Riemann zeta function						Riemann zeta function with prime 2 removed
Tuning			Strength	Closest EDO		Tuning		Strength	Closest EDO
ZPI	Steps per octave	Step size (cents)	Height	EDO	Octave (cents)	Steps per octave	Step size (cents)	Height	EDO	Octave (cents)
53zpi	16.3979501311478	73.1798786069366	2.518818	16edo	1170.87805771099	16.4044889390925	73.1507092025500	4.100909	16edo	1170.41134724080
71zpi	20.2248393119540	59.3329806724710	3.531097	20edo	1186.65961344942	20.2459529213541	59.2711049295348	4.137236	20edo	1185.42209859070
93zpi	24.5782550666850	48.8236449961234	2.810487	25edo	1220.59112490308	24.5738316304204	48.8324335434323	4.665720	25edo	1220.81083858581

71zpi with prime 2 removed

Approximation of harmonics in 71zpi with prime 2 removed

Harmonic		2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Error	Absolute (¢)	-14.6	-5.3	-29.2	-0.6	-19.9	+9.6	+15.5	-10.6	-15.1	-2.3	+24.8	+4.8	-5.0	-5.9	+1.0
	Relative (%)	-24.6	-8.9	-49.2	-1.0	-33.5	+16.2	+26.2	-17.8	-25.6	-3.9	+41.9	+8.1	-8.4	-9.9	+1.6
Step		20	32	40	47	52	57	61	64	67	70	73	75	77	79	81

Approximation of harmonics in 71zpi with prime 2 removed

Harmonic		17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34
Error	Absolute (¢)	+14.5	-25.1	-0.2	+29.5	+4.3	-16.9	+24.7	+10.3	-1.1	-9.8	-15.8	-19.5	-21.0	-20.4	-17.9	-13.6	-7.6	-0.0
	Relative (%)	+24.5	-42.4	-0.3	+49.8	+7.3	-28.5	+41.6	+17.3	-1.9	-16.5	-26.7	-32.9	-35.4	-34.5	-30.2	-23.0	-12.9	-0.1
Step		83	84	86	88	89	90	92	93	94	95	96	97	98	99	100	101	102	103