11-limit: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older editNewer edit →
VisualWikitext
Wikispaces>PiotrGrochowski
**Imported revision 591448544 - Original comment: **
Wikispaces>FREEZE
No edit summary
Line 1: Line 1:
<h2>IMPORTED REVISION FROM WIKISPACES</h2>
The ''11-limit'' consists of all [[JustIntonation|justly tuned]] intervals whose numerators and denominators are both products of the primes 2, 3, 5, 7 and 11. Some examples of 11-limit intervals are [[14/11|14/11]], [[11/8|11/8]], [[27/22|27/22]] and [[99/98|99/98]]. The 11 odd-limit consists of intervals whose numerators and denominators, when all factors of two have been removed, are less than or equal to 11. Reduced to an octave, these are the ratios 1/1, 12/11, 11/10, 10/9, 9/8, 8/7, 7/6, 6/5, 11/9, 5/4, 14/11, 9/7, 4/3, 11/8, 7/5, 10/7, 16/11, 3/2, 14/9, 11/7, 8/5, 18/11, 5/3, 12/7, 7/4, 16/9, 9/5, 20/11, 11/6, 2/1. In an 11-limit system, all the ratios of the 11 odd-limit can be treated as potential consonances.
This is an imported revision from Wikispaces. The revision metadata is included below for reference:<br>
: This revision was by author [[User:PiotrGrochowski|PiotrGrochowski]] and made on <tt>2016-09-08 15:27:10 UTC</tt>.<br>
: The original revision id was <tt>591448544</tt>.<br>
: The revision comment was: <tt></tt><br>
The revision contents are below, presented both in the original Wikispaces Wikitext format, and in HTML exactly as Wikispaces rendered it.<br>
<h4>Original Wikitext content:</h4>
<div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;white-space: pre-wrap ! important" class="old-revision-html">The //11-limit// consists of all [[JustIntonation|justly tuned]] intervals whose numerators and denominators are both products of the primes 2, 3, 5, 7 and 11. Some examples of 11-limit intervals are [[14_11|14/11]], [[11_8|11/8]], [[27_22|27/22]] and [[99_98|99/98]]. The 11 odd-limit consists of intervals whose numerators and denominators, when all factors of two have been removed, are less than or equal to 11. Reduced to an octave, these are the ratios 1/1, 12/11, 11/10, 10/9, 9/8, 8/7, 7/6, 6/5, 11/9, 5/4, 14/11, 9/7, 4/3, 11/8, 7/5, 10/7, 16/11, 3/2, 14/9, 11/7, 8/5, 18/11, 5/3, 12/7, 7/4, 16/9, 9/5, 20/11, 11/6, 2/1. In an 11-limit system, all the ratios of the 11 odd-limit can be treated as potential consonances.


|| ratio || harmonic solfege ||
{| class="wikitable"
|| 12/11 || fu-sol ||
|-
|| 11/10 || mi-fu ||
| | ratio
|| 10/9 || re-mi ||
| | harmonic solfege
|| 9/8 || do-re ||
|-
|| 8/7 || ta-do ||
| | 12/11
|| 7/6 || sol-ta ||
| | fu-sol
|| 6/5 || mi-sol, ti-re ||
|-
|| 11/9 || re-fu ||
| | 11/10
|| 5/4 || do-mi ||
| | mi-fu
|| 14/11 || fu-ta ||
|-
|| 9/7 || ta-re ||
| | 10/9
|| 4/3 || do-fa ||
| | re-mi
|| 11/8 || do-fu ||
|-
|| 7/5 || mi-ta ||
| | 9/8
|| 10/7 || ta-mi ||
| | do-re
|| 16/11 || fu-do ||
|-
|| 3/2 || do-sol ||
| | 8/7
|| 14/9 || re-ta ||
| | ta-do
|| 11/7 || ta-fu ||
|-
|| 8/5 || mi-do ||
| | 7/6
|| 18/11 || fu-re ||
| | sol-ta
|| 5/3 || sol-mi ||
|-
|| 12/7 || ta-sol ||
| | 6/5
|| 7/4 || do-ta ||
| | mi-sol, ti-re
|| 16/9 || re-do ||
|-
|| 9/5 || mi-re ||
| | 11/9
|| 20/11 || fu-mi ||
| | re-fu
|| 11/6 || sol-fu ||
|-
|| 2/1 || do-do ||
| | 5/4
| | do-mi
|-
| | 14/11
| | fu-ta
|-
| | 9/7
| | ta-re
|-
| | 4/3
| | do-fa
|-
| | 11/8
| | do-fu
|-
| | 7/5
| | mi-ta
|-
| | 10/7
| | ta-mi
|-
| | 16/11
| | fu-do
|-
| | 3/2
| | do-sol
|-
| | 14/9
| | re-ta
|-
| | 11/7
| | ta-fu
|-
| | 8/5
| | mi-do
|-
| | 18/11
| | fu-re
|-
| | 5/3
| | sol-mi
|-
| | 12/7
| | ta-sol
|-
| | 7/4
| | do-ta
|-
| | 16/9
| | re-do
|-
| | 9/5
| | mi-re
|-
| | 20/11
| | fu-mi
|-
| | 11/6
| | sol-fu
|-
| | 2/1
| | do-do
|}


While the [[7-limit]] introduces subminor and supermajor intervals, which can sound like dramatic inflections of the familiar interval categories of [[12edo]], the 11-limit introduces neutral intervals, [[superfourth]]s and [[subfifth]]s, which fall in between major, minor and perfect [[interval category|interval categories]] and thus demand new distinctions. It is thus inescapably xenharmonic.
While the [[7-limit|7-limit]] introduces subminor and supermajor intervals, which can sound like dramatic inflections of the familiar interval categories of [[12edo|12edo]], the 11-limit introduces neutral intervals, [[Superfourth|superfourth]]s and [[Subfifth|subfifth]]s, which fall in between major, minor and perfect [[interval_category|interval categories]] and thus demand new distinctions. It is thus inescapably xenharmonic.


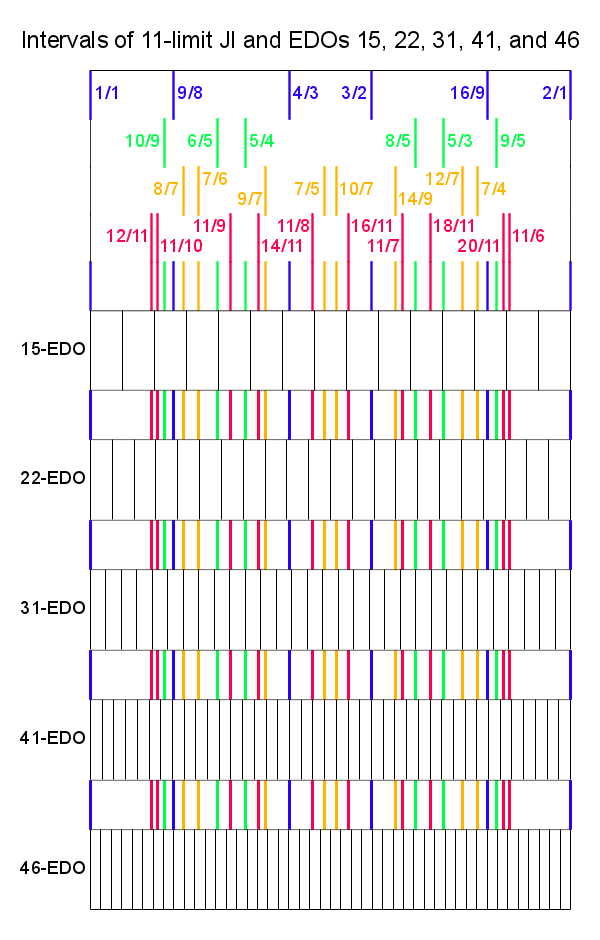
Relative to their size, [[edo]]s which do (relatively) well in supporting 11-limit intervals are: [[1edo]], [[2edo]], [[3edo]], [[4edo]], [[5edo]], [[6edo]], [[7edo]], [[9edo]], [[10edo]], [[12edo]], [[15edo]], [[22edo]], [[26edo]], [[31edo]], [[41edo]], [[63edo]], [[72edo]], [[87edo]], [[109edo]], [[161edo]].
Relative to their size, [[EDO|edo]]s which do (relatively) well in supporting 11-limit intervals are: [[1edo|1edo]], [[2edo|2edo]], [[3edo|3edo]], [[4edo|4edo]], [[5edo|5edo]], [[6edo|6edo]], [[7edo|7edo]], [[9edo|9edo]], [[10edo|10edo]], [[12edo|12edo]], [[15edo|15edo]], [[22edo|22edo]], [[26edo|26edo]], [[31edo|31edo]], [[41edo|41edo]], [[63edo|63edo]], [[72edo|72edo]], [[87edo|87edo]], [[109edo|109edo]], [[161edo|161edo]].


[[image:11-limit_compare.png]]
[[File:11-limit_compare.png|alt=11-limit_compare.png|11-limit_compare.png]]


==Intervals==  
==Intervals==
Some of the simplest intervals of 11 include:
Some of the simplest intervals of 11 include:


|| Interval || Cents Value ||
{| class="wikitable"
|| [[12_11|12/11]] || 150.637 ||
|-
|| [[11_10|11/10]] || 165.004 ||
| | Interval
|| [[11_9|11/9]] || 347.408 ||
| | Cents Value
|| [[14_11|14/11]] || 417.508 ||
|-
|| [[15_11|15/11]] || 536.951 ||
| | [[12/11|12/11]]
|| [[11_8|11/8]] || 551.318 ||
| | 150.637
|| [[16_11|16/11]] || 648.682 ||
|-
|| [[22_15|22/15]] || 663.049 ||
| | [[11/10|11/10]]
|| [[11_7|11/7]] || 782.492 ||
| | 165.004
|| [[18_11|18/11]] || 852.592 ||
|-
|| [[20_11|20/11]] || 1034.996 ||
| | [[11/9|11/9]]
|| [[11_6|11/6]] || 1049.363 ||
| | 347.408
See: [[Gallery of Just Intervals]]
|-
| | [[14/11|14/11]]
| | 417.508
|-
| | [[15/11|15/11]]
| | 536.951
|-
| | [[11/8|11/8]]
| | 551.318
|-
| | [[16/11|16/11]]
| | 648.682
|-
| | [[22/15|22/15]]
| | 663.049
|-
| | [[11/7|11/7]]
| | 782.492
|-
| | [[18/11|18/11]]
| | 852.592
|-
| | [[20/11|20/11]]
| | 1034.996
|-
| | [[11/6|11/6]]
| | 1049.363
|}
See: [[Gallery_of_Just_Intervals|Gallery of Just Intervals]]


=Music=  
=Music=
[[http://sonic-arts.org/hill/10-passages-ji/10-passages-ji.htm|Study #3]] [[http://sonic-arts.org/hill/10-passages-ji/04_hill_study-3.mp3|play]] by [[Dave Hill]]
[http://sonic-arts.org/hill/10-passages-ji/10-passages-ji.htm Study #3] [http://sonic-arts.org/hill/10-passages-ji/04_hill_study-3.mp3 play] by [[Dave_Hill|Dave Hill]]
[[http://sonic-arts.org/hill/10-passages-ji/10-passages-ji.htm|Brief 11-ratio composition]] [[http://sonic-arts.org/hill/10-passages-ji/09_hill_brief-11-ratio-composition.mp3|play]] by Dave Hill
[[http://micro.soonlabel.com/just/11-limit/20120210-piano-11-limit.mp3|11 Limit Piano]] by [[Chris Vaisvil]]
[[https://soundcloud.com/andrew_heathwaite/11-limit-singtervals|11-limit singtervals]] by [[Andrew Heathwaite]]


=See also=
[http://sonic-arts.org/hill/10-passages-ji/10-passages-ji.htm Brief 11-ratio composition] [http://sonic-arts.org/hill/10-passages-ji/09_hill_brief-11-ratio-composition.mp3 play] by Dave Hill
[[Harmonic Limit]]
[[media type="custom" key="12438854"]]</pre></div>
<h4>Original HTML content:</h4>
<div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;width:200%;white-space: pre-wrap ! important" class="old-revision-html">&lt;html&gt;&lt;head&gt;&lt;title&gt;11-limit&lt;/title&gt;&lt;/head&gt;&lt;body&gt;The &lt;em&gt;11-limit&lt;/em&gt; consists of all &lt;a class="wiki_link" href="/JustIntonation"&gt;justly tuned&lt;/a&gt; intervals whose numerators and denominators are both products of the primes 2, 3, 5, 7 and 11. Some examples of 11-limit intervals are &lt;a class="wiki_link" href="/14_11"&gt;14/11&lt;/a&gt;, &lt;a class="wiki_link" href="/11_8"&gt;11/8&lt;/a&gt;, &lt;a class="wiki_link" href="/27_22"&gt;27/22&lt;/a&gt; and &lt;a class="wiki_link" href="/99_98"&gt;99/98&lt;/a&gt;. The 11 odd-limit consists of intervals whose numerators and denominators, when all factors of two have been removed, are less than or equal to 11. Reduced to an octave, these are the ratios 1/1, 12/11, 11/10, 10/9, 9/8, 8/7, 7/6, 6/5, 11/9, 5/4, 14/11, 9/7, 4/3, 11/8, 7/5, 10/7, 16/11, 3/2, 14/9, 11/7, 8/5, 18/11, 5/3, 12/7, 7/4, 16/9, 9/5, 20/11, 11/6, 2/1. In an 11-limit system, all the ratios of the 11 odd-limit can be treated as potential consonances.&lt;br /&gt;
&lt;br /&gt;


[http://micro.soonlabel.com/just/11-limit/20120210-piano-11-limit.mp3 11 Limit Piano] by [[Chris_Vaisvil|Chris Vaisvil]]


&lt;table class="wiki_table"&gt;
[https://soundcloud.com/andrew_heathwaite/11-limit-singtervals 11-limit singtervals] by [[Andrew_Heathwaite|Andrew Heathwaite]]
    &lt;tr&gt;
        &lt;td&gt;ratio&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;harmonic solfege&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;12/11&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;fu-sol&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;11/10&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;mi-fu&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;10/9&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;re-mi&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;9/8&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;do-re&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;8/7&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;ta-do&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;7/6&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;sol-ta&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;6/5&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;mi-sol, ti-re&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;11/9&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;re-fu&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;5/4&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;do-mi&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;14/11&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;fu-ta&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;9/7&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;ta-re&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;4/3&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;do-fa&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;11/8&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;do-fu&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;7/5&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;mi-ta&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;10/7&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;ta-mi&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;16/11&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;fu-do&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;3/2&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;do-sol&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;14/9&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;re-ta&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;11/7&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;ta-fu&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;8/5&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;mi-do&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;18/11&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;fu-re&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;5/3&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;sol-mi&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;12/7&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;ta-sol&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;7/4&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;do-ta&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;16/9&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;re-do&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;9/5&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;mi-re&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;20/11&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;fu-mi&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;11/6&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;sol-fu&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;2/1&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;do-do&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
&lt;/table&gt;


&lt;br /&gt;
=See also=
While the &lt;a class="wiki_link" href="/7-limit"&gt;7-limit&lt;/a&gt; introduces subminor and supermajor intervals, which can sound like dramatic inflections of the familiar interval categories of &lt;a class="wiki_link" href="/12edo"&gt;12edo&lt;/a&gt;, the 11-limit introduces neutral intervals, &lt;a class="wiki_link" href="/superfourth"&gt;superfourth&lt;/a&gt;s and &lt;a class="wiki_link" href="/subfifth"&gt;subfifth&lt;/a&gt;s, which fall in between major, minor and perfect &lt;a class="wiki_link" href="/interval%20category"&gt;interval categories&lt;/a&gt; and thus demand new distinctions. It is thus inescapably xenharmonic.&lt;br /&gt;
[[Harmonic_Limit|Harmonic Limit]]
&lt;br /&gt;
Relative to their size, &lt;a class="wiki_link" href="/edo"&gt;edo&lt;/a&gt;s which do (relatively) well in supporting 11-limit intervals are: &lt;a class="wiki_link" href="/1edo"&gt;1edo&lt;/a&gt;, &lt;a class="wiki_link" href="/2edo"&gt;2edo&lt;/a&gt;, &lt;a class="wiki_link" href="/3edo"&gt;3edo&lt;/a&gt;, &lt;a class="wiki_link" href="/4edo"&gt;4edo&lt;/a&gt;, &lt;a class="wiki_link" href="/5edo"&gt;5edo&lt;/a&gt;, &lt;a class="wiki_link" href="/6edo"&gt;6edo&lt;/a&gt;, &lt;a class="wiki_link" href="/7edo"&gt;7edo&lt;/a&gt;, &lt;a class="wiki_link" href="/9edo"&gt;9edo&lt;/a&gt;, &lt;a class="wiki_link" href="/10edo"&gt;10edo&lt;/a&gt;, &lt;a class="wiki_link" href="/12edo"&gt;12edo&lt;/a&gt;, &lt;a class="wiki_link" href="/15edo"&gt;15edo&lt;/a&gt;, &lt;a class="wiki_link" href="/22edo"&gt;22edo&lt;/a&gt;, &lt;a class="wiki_link" href="/26edo"&gt;26edo&lt;/a&gt;, &lt;a class="wiki_link" href="/31edo"&gt;31edo&lt;/a&gt;, &lt;a class="wiki_link" href="/41edo"&gt;41edo&lt;/a&gt;, &lt;a class="wiki_link" href="/63edo"&gt;63edo&lt;/a&gt;, &lt;a class="wiki_link" href="/72edo"&gt;72edo&lt;/a&gt;, &lt;a class="wiki_link" href="/87edo"&gt;87edo&lt;/a&gt;, &lt;a class="wiki_link" href="/109edo"&gt;109edo&lt;/a&gt;, &lt;a class="wiki_link" href="/161edo"&gt;161edo&lt;/a&gt;.&lt;br /&gt;
&lt;br /&gt;
&lt;!-- ws:start:WikiTextLocalImageRule:269:&amp;lt;img src=&amp;quot;/file/view/11-limit_compare.png/354832066/11-limit_compare.png&amp;quot; alt=&amp;quot;&amp;quot; title=&amp;quot;&amp;quot; /&amp;gt; --&gt;&lt;img src="/file/view/11-limit_compare.png/354832066/11-limit_compare.png" alt="11-limit_compare.png" title="11-limit_compare.png" /&gt;&lt;!-- ws:end:WikiTextLocalImageRule:269 --&gt;&lt;br /&gt;
&lt;br /&gt;
&lt;!-- ws:start:WikiTextHeadingRule:1:&amp;lt;h2&amp;gt; --&gt;&lt;h2 id="toc0"&gt;&lt;a name="x-Intervals"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:1 --&gt;Intervals&lt;/h2&gt;
Some of the simplest intervals of 11 include:&lt;br /&gt;
&lt;br /&gt;


 
[[Category:11-limit]]
&lt;table class="wiki_table"&gt;
[[Category:example]]
    &lt;tr&gt;
[[Category:interval]]
        &lt;td&gt;Interval&lt;br /&gt;
[[Category:limit]]
&lt;/td&gt;
[[Category:listen]]
        &lt;td&gt;Cents Value&lt;br /&gt;
[[Category:prime_limit]]
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;&lt;a class="wiki_link" href="/12_11"&gt;12/11&lt;/a&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;150.637&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;&lt;a class="wiki_link" href="/11_10"&gt;11/10&lt;/a&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;165.004&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;&lt;a class="wiki_link" href="/11_9"&gt;11/9&lt;/a&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;347.408&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;&lt;a class="wiki_link" href="/14_11"&gt;14/11&lt;/a&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;417.508&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;&lt;a class="wiki_link" href="/15_11"&gt;15/11&lt;/a&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;536.951&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;&lt;a class="wiki_link" href="/11_8"&gt;11/8&lt;/a&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;551.318&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;&lt;a class="wiki_link" href="/16_11"&gt;16/11&lt;/a&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;648.682&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;&lt;a class="wiki_link" href="/22_15"&gt;22/15&lt;/a&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;663.049&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;&lt;a class="wiki_link" href="/11_7"&gt;11/7&lt;/a&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;782.492&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;&lt;a class="wiki_link" href="/18_11"&gt;18/11&lt;/a&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;852.592&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;&lt;a class="wiki_link" href="/20_11"&gt;20/11&lt;/a&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;1034.996&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td&gt;&lt;a class="wiki_link" href="/11_6"&gt;11/6&lt;/a&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;1049.363&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
&lt;/table&gt;
 
See: &lt;a class="wiki_link" href="/Gallery%20of%20Just%20Intervals"&gt;Gallery of Just Intervals&lt;/a&gt;&lt;br /&gt;
&lt;br /&gt;
&lt;!-- ws:start:WikiTextHeadingRule:3:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc1"&gt;&lt;a name="Music"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:3 --&gt;Music&lt;/h1&gt;
&lt;a class="wiki_link_ext" href="http://sonic-arts.org/hill/10-passages-ji/10-passages-ji.htm" rel="nofollow"&gt;Study #3&lt;/a&gt; &lt;a class="wiki_link_ext" href="http://sonic-arts.org/hill/10-passages-ji/04_hill_study-3.mp3" rel="nofollow"&gt;play&lt;/a&gt; by &lt;a class="wiki_link" href="/Dave%20Hill"&gt;Dave Hill&lt;/a&gt;&lt;br /&gt;
&lt;a class="wiki_link_ext" href="http://sonic-arts.org/hill/10-passages-ji/10-passages-ji.htm" rel="nofollow"&gt;Brief 11-ratio composition&lt;/a&gt; &lt;a class="wiki_link_ext" href="http://sonic-arts.org/hill/10-passages-ji/09_hill_brief-11-ratio-composition.mp3" rel="nofollow"&gt;play&lt;/a&gt; by Dave Hill&lt;br /&gt;
&lt;a class="wiki_link_ext" href="http://micro.soonlabel.com/just/11-limit/20120210-piano-11-limit.mp3" rel="nofollow"&gt;11 Limit Piano&lt;/a&gt; by &lt;a class="wiki_link" href="/Chris%20Vaisvil"&gt;Chris Vaisvil&lt;/a&gt;&lt;br /&gt;
&lt;a class="wiki_link_ext" href="https://soundcloud.com/andrew_heathwaite/11-limit-singtervals" rel="nofollow"&gt;11-limit singtervals&lt;/a&gt; by &lt;a class="wiki_link" href="/Andrew%20Heathwaite"&gt;Andrew Heathwaite&lt;/a&gt;&lt;br /&gt;
&lt;br /&gt;
&lt;!-- ws:start:WikiTextHeadingRule:5:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc2"&gt;&lt;a name="See also"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:5 --&gt;See also&lt;/h1&gt;
&lt;a class="wiki_link" href="/Harmonic%20Limit"&gt;Harmonic Limit&lt;/a&gt;&lt;br /&gt;
&lt;!-- ws:start:WikiTextMediaRule:0:&amp;lt;img src=&amp;quot;http://www.wikispaces.com/site/embedthumbnail/custom/12438854?h=0&amp;amp;w=0&amp;quot; class=&amp;quot;WikiMedia WikiMediaCustom&amp;quot; id=&amp;quot;wikitext@@media@@type=&amp;amp;quot;custom&amp;amp;quot; key=&amp;amp;quot;12438854&amp;amp;quot;&amp;quot; title=&amp;quot;Custom Media&amp;quot;/&amp;gt; --&gt;&lt;script type="text/javascript" src="http://webplayer.yahooapis.com/player.js"&gt;
&lt;/script&gt;&lt;!-- ws:end:WikiTextMediaRule:0 --&gt;&lt;/body&gt;&lt;/html&gt;</pre></div>

Revision as of 00:00, 17 July 2018

The 11-limit consists of all justly tuned intervals whose numerators and denominators are both products of the primes 2, 3, 5, 7 and 11. Some examples of 11-limit intervals are 14/11, 11/8, 27/22 and 99/98. The 11 odd-limit consists of intervals whose numerators and denominators, when all factors of two have been removed, are less than or equal to 11. Reduced to an octave, these are the ratios 1/1, 12/11, 11/10, 10/9, 9/8, 8/7, 7/6, 6/5, 11/9, 5/4, 14/11, 9/7, 4/3, 11/8, 7/5, 10/7, 16/11, 3/2, 14/9, 11/7, 8/5, 18/11, 5/3, 12/7, 7/4, 16/9, 9/5, 20/11, 11/6, 2/1. In an 11-limit system, all the ratios of the 11 odd-limit can be treated as potential consonances.

ratio harmonic solfege
12/11 fu-sol
11/10 mi-fu
10/9 re-mi
9/8 do-re
8/7 ta-do
7/6 sol-ta
6/5 mi-sol, ti-re
11/9 re-fu
5/4 do-mi
14/11 fu-ta
9/7 ta-re
4/3 do-fa
11/8 do-fu
7/5 mi-ta
10/7 ta-mi
16/11 fu-do
3/2 do-sol
14/9 re-ta
11/7 ta-fu
8/5 mi-do
18/11 fu-re
5/3 sol-mi
12/7 ta-sol
7/4 do-ta
16/9 re-do
9/5 mi-re
20/11 fu-mi
11/6 sol-fu
2/1 do-do

While the 7-limit introduces subminor and supermajor intervals, which can sound like dramatic inflections of the familiar interval categories of 12edo, the 11-limit introduces neutral intervals, superfourths and subfifths, which fall in between major, minor and perfect interval categories and thus demand new distinctions. It is thus inescapably xenharmonic.

Relative to their size, edos which do (relatively) well in supporting 11-limit intervals are: 1edo, 2edo, 3edo, 4edo, 5edo, 6edo, 7edo, 9edo, 10edo, 12edo, 15edo, 22edo, 26edo, 31edo, 41edo, 63edo, 72edo, 87edo, 109edo, 161edo.

11-limit_compare.png

Intervals

Some of the simplest intervals of 11 include:

Interval Cents Value
12/11 150.637
11/10 165.004
11/9 347.408
14/11 417.508
15/11 536.951
11/8 551.318
16/11 648.682
22/15 663.049
11/7 782.492
18/11 852.592
20/11 1034.996
11/6 1049.363

See: Gallery of Just Intervals

Music

Study #3 play by Dave Hill

Brief 11-ratio composition play by Dave Hill

11 Limit Piano by Chris Vaisvil

11-limit singtervals by Andrew Heathwaite

See also

Harmonic Limit

Retrieved from "https://en.xen.wiki/index.php?title=11-limit&oldid=54"