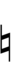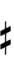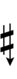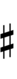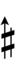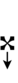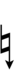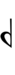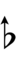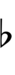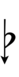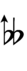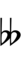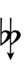69edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older editNewer edit →
VisualWikitext
Dave Keenan (talk | contribs)
autopatrolled
1,671 edits
→Sagittal notation: Moved the explanation of ≈ to the end of the section.
ArrowHead294 (talk | contribs)
14,512 edits
mNo edit summary
Line 1: Line 1:
{{Infobox ET}}
{{Infobox ET}}
{{EDO intro|69}} Nice.
{{ED intro}}
 
== Theory ==
== Theory ==
69edo has been called "the love-child of [[23edo]] and [[quarter-comma meantone]]". As a meantone system, it is on the flat side, with a fifth of 695.652 cents. Such a fifth is closer to [[2/7-comma meantone]] than 1/4-comma, and is nearly identical to that of "Synch-Meantone", or Wilson's equal beating meantone, wherein the perfect fifth and the major third beat at equal rates. Therefore 69edo can be treated as a closed system of Synch-Meantone for most purposes.
69edo has been called "the love-child of [[23edo]] and [[quarter-comma meantone]]". As a meantone system, it is on the flat side, with a fifth of 695.652{{c}}. Such a fifth is closer to [[2/7-comma meantone]] than 1/4-comma, and is nearly identical to that of "Synch-Meantone", or Wilson's equal beating meantone, wherein the perfect fifth and the major third beat at equal rates. Therefore 69edo can be treated as a closed system of Synch-Meantone for most purposes.


69edo offers two kinds of meantone 12-tone scales. One is the raw meantone scale, which has a 7:4 step ratio, and other is period-3 [[Meantone family#Lithium|lithium]] scale, which has a 6:5 step ratio and stems from a temperament tempering out 3125/3087 along with 81/80. It should be noted that while the lithium scale has a meantone fifth, it produces a [[3L 6s|tcherepnin]] scale instead of traditional diatonic.
69edo offers two kinds of meantone 12-tone scales. One is the raw meantone scale, which has a 7:4 step ratio, and other is period-3 [[Meantone family#Lithium|lithium]] scale, which has a 6:5 step ratio and stems from a temperament tempering out 3125/3087 along with 81/80. It should be noted that while the lithium scale has a meantone fifth, it produces a [[3L 6s|tcherepnin]] scale instead of traditional diatonic.


In the [[7-limit]] it is a [[mohajira]] system, tempering out 6144/6125, but not a septimal meantone system, as [[126/125]] maps to one step. In the 11-limit it tempers out [[99/98]], and supports the 31&69 variant of mohajira, identical to the standard 11-limit mohajira in [[31edo]] but not in 69.
In the [[7-limit]] it is a [[mohajira]] system, tempering out 6144/6125, but not a septimal meantone system, as [[126/125]] maps to one step. In the 11-limit it tempers out [[99/98]], and supports the {{nowrap|31 & 69}} variant of mohajira, identical to the standard 11-limit mohajira in [[31edo]] but not in 69.


The [[concoctic scale]] for 69edo is 22\69, and the corresponding rank two temperament is 22 & 69, defined by tempering out the [-41, 1, 17⟩ comma in the 5-limit.
The [[concoctic scale]] for 69edo is 22\69, and the corresponding rank two temperament is {{nowrap|22 & 69}}, defined by tempering out the [-41, 1, 17⟩ comma in the 5-limit.


=== Odd harmonics ===
=== Odd harmonics ===
Line 26: Line 25:
! Error (abs, [[cent|¢]])
! Error (abs, [[cent|¢]])
|-
|-
|0
| 0
|Natural Unison, 1
| Natural Unison, 1
|0.000
| 0.000
|[[1/1]]
| [[1/1]]
|0.000
| 0.000
|-
|-
|1
| 1
|Ptolemy's comma
| Ptolemy's comma
|17.391
| 17.391
|[[100/99]]
| [[100/99]]
| -0.008
| −0.008
|-
|-
|2
| 2
|Jubilisma, lesser septimal sixth tone
| Jubilisma, lesser septimal sixth tone
|34.783
| 34.783
|[[50/49]], [[101/99]]
| [[50/49]], [[101/99]]
| -0.193, 0.157
| −0.193, 0.157
|-
|-
|3
| 3
|lesser septendecimal quartertone, _____
| lesser septendecimal quartertone, _____
|52.174
| 52.174
|[[34/33]], [[101/98]]
| [[34/33]], [[101/98]]
| 0.491, -0.028
| 0.491, −0.028
|-
|-
|4
| 4
|_____
| _____
|69.565
| 69.565
|[[76/73]]
| [[76/73]]
| -0.158
| −0.158
|-
|-
|5
| 5
|Small undevicesimal semitone
| Small undevicesimal semitone
|86.957
| 86.957
|[[20/19]]
| [[20/19]]
| -1.844
| −1.844
|-
|-
|6
| 6
|Large septendecimal semitone
| Large septendecimal semitone
|104.348
| 104.348
|[[17/16]]
| [[17/16]]
| -0.608
| −0.608
|-
|-
|7
| 7
|Septimal diatonic semitone
| Septimal diatonic semitone
|121.739
| 121.739
|[[15/14]]
| [[15/14]]
|2.296
| 2.296
|-
|-
|8
| 8
|Tridecimal neutral second
| Tridecimal neutral second
|139.130
| 139.130
|[[13/12]]
| [[13/12]]
|0.558
| 0.558
|-
|-
|9
| 9
|Vicesimotertial neutral second
| Vicesimotertial neutral second
|156.522
| 156.522
|[[23/21]]
| [[23/21]]
| -0.972
| −0.972
|-
|-
|10
| 10
| Undevicesimal large neutral second, undevicesimal whole tone
| Undevicesimal large neutral second, undevicesimal whole tone
|173.913
| 173.913
|[[21/19]]
| [[21/19]]
|0.645
| 0.645
|-
|-
|11
| 11
|Quasi-meantone
| Quasi-meantone
|191.304
| 191.304
|[[19/17]]
| [[19/17]]
| -1.253
| −1.253
|-
|-
|12
| 12
|Whole tone
| Whole tone
|208.696
| 208.696
|[[9/8]]
| [[9/8]]
|4.786
| 4.786
|-
|-
|13
| 13
|Septimal whole tone
| Septimal whole tone
|226.087
| 226.087
|[[8/7]]
| [[8/7]]
| -5.087
| −5.087
|-
|-
|14
| 14
|Vicesimotertial semifourth
| Vicesimotertial semifourth
|243.478
| 243.478
|[[23/20]]
| [[23/20]]
|1.518
| 1.518
|-
|-
|15
| 15
|Subminor third, undetricesimal subminor third
| Subminor third, undetricesimal subminor third
|260.870
| 260.870
|[[7/6]], [[29/25]]
| [[7/6]], [[29/25]]
| -6.001, 3.920
| −6.001, 3.920
|-
|-
|16
| 16
| Vicesimotertial subminor third
| Vicesimotertial subminor third
|278.261
| 278.261
|[[27/23]]
| [[27/23]]
|0.670
| 0.670
|-
|-
|17
| 17
|Pythagorean minor third
| Pythagorean minor third
|295.652
| 295.652
|[[32/27]]
| [[32/27]]
|1.517
| 1.517
|-
|-
|18
| 18
|Classic minor third
| Classic minor third
|313.043
| 313.043
|[[6/5]]
| [[6/5]]
| -2.598
| −2.598
|-
|-
|19
| 19
|Vicesimotertial supraminor third
| Vicesimotertial supraminor third
|330.435
| 330.435
|[[23/19]]
| [[23/19]]
| -0.327
| −0.327
|-
|-
|20
| 20
|Undecimal neutral third
| Undecimal neutral third
|347.826
| 347.826
|[[11/9]]
| [[11/9]]
|0.418
| 0.418
|-
|-
|21
| 21
|Septendecimal submajor third
| Septendecimal submajor third
|365.217
| 365.217
|[[21/17]]
| [[21/17]]
| -0.608
| −0.608
|-
|-
|22
| 22
|Classic major third
| Classic major third
|382.609
| 382.609
|[[5/4]]
| [[5/4]]
| -3.705
| −3.705
|-
|-
|23
| 23
| Undetricesimal major third, Septendecimal major third
| Undetricesimal major third, Septendecimal major third
|400.000
| 400.000
|[[29/23]], [[34/27]]
| [[29/23]], [[34/27]]
| -1.303, 0.910
| −1.303, 0.910
|-
|-
|24
| 24
|Undecimal major third
| Undecimal major third
|417.391
| 417.391
|[[14/11]]
| [[14/11]]
| -0.117
| −0.117
|-
|-
|25
| 25
|Supermajor third
| Supermajor third
|434.783
| 434.783
|[[9/7]]
| [[9/7]]
| -0.301
| −0.301
|-
|-
|26
| 26
|Barbados third
| Barbados third
|452.174
| 452.174
|[[13/10]]
| [[13/10]]
| -2.040
| −2.040
|-
|-
|27
| 27
|Septimal sub-fourth
| Septimal sub-fourth
|469.565
| 469.565
|[[21/16]]
| [[21/16]]
| -1.216
| −1.216
|-
|-
|28
| 28
|_____
| _____
|486.957
| 486.957
|[[53/40]]
| [[53/40]]
| -0.234
| −0.234
|-
|-
|29
| 29
|Just perfect fourth
| Just perfect fourth
|504.348
| 504.348
|[[4/3]]
| [[4/3]]
|6.303
| 6.303
|-
|-
|30
| 30
|Vicesimotertial acute fourth
| Vicesimotertial acute fourth
|521.739
| 521.739
|[[23/17]]
| [[23/17]]
| -1.580
| −1.580
|-
|-
|31
| 31
|Undecimal augmented fourth
| Undecimal augmented fourth
|539.130
| 539.130
|[[15/11]]
| [[15/11]]
|2.180
| 2.180
|-
|-
|32
| 32
|Undecimal superfourth, undetricesimal superfourth
| Undecimal superfourth, undetricesimal superfourth
|556.522
| 556.522
|[[11/8]], [[29/21]]
| [[11/8]], [[29/21]]
|5.204, -2.275
| 5.204, −2.275
|-
|-
|33
| 33
|Narrow tritone, classic augmented fourth
| Narrow tritone, classic augmented fourth
|573.913
| 573.913
|[[7/5]], [[25/18]]
| [[7/5]], [[25/18]]
| -8.600, 5.196
| −8.600, 5.196
|-
|-
|34
| 34
|_____
| _____
|591.304
| 591.304
|[[31/22]]
| [[31/22]]
| -2.413
| −2.413
|-
|-
|35
| 35
|High tritone, undevicesimal tritone
| High tritone, undevicesimal tritone
|608.696
| 608.696
|[[10/7]], [[27/19]]
| [[10/7]], [[27/19]]
| -8.792, 0.344
| −8.792, 0.344
|-
|-
|36
| 36
|_____
| _____
|626.087
| 626.087
|[[33/23]]
| [[33/23]]
|1.088
| 1.088
|-
|-
|37
| 37
| Undetricesimal tritone
| Undetricesimal tritone
|643.478
| 643.478
|[[29/20]]
| [[29/20]]
|0.215
| 0.215
|-
|-
|38
| 38
| Undevicesimal diminished fifth, undecimal diminished fifth
| Undevicesimal diminished fifth, undecimal diminished fifth
|660.870
| 660.870
|[[19/13]], [[22/15]]
| [[19/13]], [[22/15]]
|3.884, -2.180
| 3.884, −2.180
|-
|-
|39
| 39
|Vicesimotertial grave fifth, _____
| Vicesimotertial grave fifth, _____
|678.261
| 678.261
|[[34/23]], [[37/25]]
| [[34/23]], [[37/25]]
|1.580, -0.456
| 1.580, −0.456
|-
|-
|40
| 40
|Just perfect fifth
| Just perfect fifth
|695.652
| 695.652
|[[3/2]]
| [[3/2]]
| -6.303
| −6.303
|-
|-
|41
| 41
|_____
| _____
|713.043
| 713.043
|[[80/53]]
| [[80/53]]
|0.234
| 0.234
|-
|-
|42
| 42
|Super-fifth, undetricesimal super-fifth
| Super-fifth, undetricesimal super-fifth
|730.435
| 730.435
|[[32/21]], [[29/19]]
| [[32/21]], [[29/19]]
|1.216, -1.630
| 1.216, −1.630
|-
|-
|43
| 43
|Septendecimal subminor sixth
| Septendecimal subminor sixth
|747.826
| 747.826
|[[17/11]]
| [[17/11]]
| -5.811
| −5.811
|-
|-
|44
| 44
|Subminor sixth
| Subminor sixth
|765.217
| 765.217
|[[14/9]]
| [[14/9]]
|0.301
| 0.301
|-
|-
|45
| 45
|Undecimal minor sixth
| Undecimal minor sixth
|782.609
| 782.609
|[[11/7]]
| [[11/7]]
|0.117
| 0.117
|-
|-
|46
| 46
| Septendecimal subminor sixth
| Septendecimal subminor sixth
|800.000
| 800.000
|[[27/17]]
| [[27/17]]
| -0.910
| −0.910
|-
|-
|47
| 47
|Classic minor sixth
| Classic minor sixth
|817.391
| 817.391
|[[8/5]]
| [[8/5]]
|3.705
| 3.705
|-
|-
|48
| 48
|Septendecimal supraminor sixth
| Septendecimal supraminor sixth
|834.783
| 834.783
|[[34/21]]
| [[34/21]]
|0.608
| 0.608
|-
|-
|49
| 49
|Undecimal neutral sixth
| Undecimal neutral sixth
|852.174
| 852.174
|[[18/11]]
| [[18/11]]
| -0.418
| −0.418
|-
|-
|50
| 50
|Vicesimotertial submajor sixth
| Vicesimotertial submajor sixth
|869.565
| 869.565
|[[38/23]]
| [[38/23]]
|0.327
| 0.327
|-
|-
|51
| 51
|Classic major sixth
| Classic major sixth
|886.957
| 886.957
|[[5/3]]
| [[5/3]]
|2.598
| 2.598
|-
|-
|52
| 52
|Pythagorean major sixth
| Pythagorean major sixth
|904.348
| 904.348
|[[27/16]]
| [[27/16]]
| -1.517
| −1.517
|-
|-
|53
| 53
|Septendecimal major sixth, undetricesimal major sixth
| Septendecimal major sixth, undetricesimal major sixth
|921.739
| 921.739
|[[17/10]], [[29/17]]
| [[17/10]], [[29/17]]
|3.097, -2.883
| 3.097, −2.883
|-
|-
|54
| 54
|Supermajor sixth, undetricesimal supermajor sixth
| Supermajor sixth, undetricesimal supermajor sixth
|939.130
| 939.130
|[[12/7]], [[50/29]]
| [[12/7]], [[50/29]]
|6.001, -3.920
| 6.001, −3.920
|-
|-
|55
| 55
|Vicesimotertial supermajor sixth
| Vicesimotertial supermajor sixth
|956.522
| 956.522
|[[40/23]]
| [[40/23]]
| -1.518
| −1.518
|-
|-
|56
| 56
|Harmonic seventh
| Harmonic seventh
|973.913
| 973.913
|[[7/4]]
| [[7/4]]
|5.087
| 5.087
|-
|-
|57
| 57
|Pythagorean minor seventh
| Pythagorean minor seventh
|991.304
| 991.304
|[[16/9]]
| [[16/9]]
| -4.786
| −4.786
|-
|-
|58
| 58
|Quasi-meantone minor seventh
| Quasi-meantone minor seventh
|1008.696
| 1008.696
|[[34/19]]
| [[34/19]]
|1.253
| 1.253
|-
|-
|59
| 59
|Minor neutral undevicesimal seventh
| Minor neutral undevicesimal seventh
|1026.087
| 1026.087
|[[38/21]]
| [[38/21]]
| -0.645
| −0.645
|-
|-
|60
| 60
|Vicesimotertial neutral seventh
| Vicesimotertial neutral seventh
|1043.478
| 1043.478
|[[42/23]]
| [[42/23]]
|0.972
| 0.972
|-
|-
|61
| 61
|Tridecimal neutral seventh
| Tridecimal neutral seventh
|1060.870
| 1060.870
|[[24/13]]
| [[24/13]]
| -0.558
| −0.558
|-
|-
|62
| 62
|Septimal diatonic major seventh
| Septimal diatonic major seventh
|1078.261
| 1078.261
|[[28/15]]
| [[28/15]]
| -2.296
| −2.296
|-
|-
|63
| 63
|Small septendecimal major seventh
| Small septendecimal major seventh
|1095.652
| 1095.652
|[[32/17]]
| [[32/17]]
|0.608
| 0.608
|-
|-
|64
| 64
|Small undevicesimal semitone
| Small undevicesimal semitone
|1113.043
| 1113.043
|[[20/19]]
| [[20/19]]
|1.844
| 1.844
|-
|-
|65
| 65
|_____
| _____
|1130.435
| 1130.435
|[[73/38]]
| [[73/38]]
|0.158
| 0.158
|-
|-
|66
| 66
| Septendecimal supermajor seventh
| Septendecimal supermajor seventh
|1147.826
| 1147.826
|[[33/17]]
| [[33/17]]
| -0.491
| −0.491
|-
|-
|67
| 67
|_____
| _____
|1165.217
| 1165.217
|[[49/25]]
| [[49/25]]
| -0.193
| −0.193
|-
|-
|68
| 68
|_____
| _____
|1182.609
| 1182.609
|[[99/50]]
| [[99/50]]
|0.008
| 0.008
|-
|-
|69
| 69
|Octave, 8
| Octave, 8
|1200.000
| 1200.000
|[[2/1]]
| [[2/1]]
|0.000
| 0.000
|}
|}
<nowiki>*</nowiki>some simpler ratios listed
<nowiki />* Some simpler ratios listed


== Notation ==
== Notation ==
=== Ups and downs notation ===
Using [[Helmholtz–Ellis]] accidentals, 69edo can also be notated using [[ups and downs notation]] along with Stein–Zimmerman [[24edo#Notation|quarter-tone]] accidentals:
{{Sharpness-sharp4}}
Here, a sharp raises by four steps, and a flat lowers by four steps, so arrows can be used to fill in the gap.


===Sagittal notation===
=== Sagittal notation ===
This notation uses the same sagittal sequence as EDOs [[62edo#Sagittal notation|62]] and [[76edo#Sagittal notation|76]].
This notation uses the same sagittal sequence as EDOs [[62edo#Sagittal notation|62]] and [[76edo#Sagittal notation|76]].
====Evo flavor====


==== Evo flavor ====
<imagemap>
<imagemap>
File:69-EDO_Evo_Sagittal.svg
File:69-EDO_Evo_Sagittal.svg
Line 464: Line 467:
</imagemap>
</imagemap>


====Revo flavor====
==== Revo flavor ====
 
<imagemap>
<imagemap>
File:69-EDO_Revo_Sagittal.svg
File:69-EDO_Revo_Sagittal.svg
Line 476: Line 478:
</imagemap>
</imagemap>


====Evo-SZ flavor====
==== Evo-SZ flavor ====
 
<imagemap>
<imagemap>
File:69-EDO_Evo-SZ_Sagittal.svg
File:69-EDO_Evo-SZ_Sagittal.svg
Line 492: Line 493:
== Regular temperament properties ==
== Regular temperament properties ==
{| class="wikitable center-4 center-5 center-6"
{| class="wikitable center-4 center-5 center-6"
|-
! rowspan="2" | [[Subgroup]]
! rowspan="2" | [[Subgroup]]
! rowspan="2" | [[Comma list|Comma List]]
! rowspan="2" | [[Comma list|Comma List]]

Revision as of 15:54, 20 February 2025

← 68edo 69edo 70edo →
Prime factorization 3 × 23
Step size 17.3913 ¢ 
Fifth 40\69 (695.652 ¢)
Semitones (A1:m2) 4:7 (69.57 ¢ : 121.7 ¢)
Dual sharp fifth 41\69 (713.043 ¢)
Dual flat fifth 40\69 (695.652 ¢)
Dual major 2nd 12\69 (208.696 ¢) (→ 4\23)
Consistency limit 5
Distinct consistency limit 5

69 equal divisions of the octave (abbreviated 69edo or 69ed2), also called 69-tone equal temperament (69tet) or 69 equal temperament (69et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 69 equal parts of about 17.4 ¢ each. Each step represents a frequency ratio of 21/69, or the 69th root of 2.

Theory

69edo has been called "the love-child of 23edo and quarter-comma meantone". As a meantone system, it is on the flat side, with a fifth of 695.652 ¢. Such a fifth is closer to 2/7-comma meantone than 1/4-comma, and is nearly identical to that of "Synch-Meantone", or Wilson's equal beating meantone, wherein the perfect fifth and the major third beat at equal rates. Therefore 69edo can be treated as a closed system of Synch-Meantone for most purposes.

69edo offers two kinds of meantone 12-tone scales. One is the raw meantone scale, which has a 7:4 step ratio, and other is period-3 lithium scale, which has a 6:5 step ratio and stems from a temperament tempering out 3125/3087 along with 81/80. It should be noted that while the lithium scale has a meantone fifth, it produces a tcherepnin scale instead of traditional diatonic.

In the 7-limit it is a mohajira system, tempering out 6144/6125, but not a septimal meantone system, as 126/125 maps to one step. In the 11-limit it tempers out 99/98, and supports the 31 & 69 variant of mohajira, identical to the standard 11-limit mohajira in 31edo but not in 69.

The concoctic scale for 69edo is 22\69, and the corresponding rank two temperament is 22 & 69, defined by tempering out the [-41, 1, 17⟩ comma in the 5-limit.

Odd harmonics

Approximation of odd harmonics in 69edo
Harmonic 3 5 7 9 11 13 15 17 19 21 23
Error Absolute (¢) -6.30 -3.71 +5.09 +4.79 +5.20 -5.75 +7.38 -0.61 -1.86 -1.22 -2.19
Relative (%) -36.2 -21.3 +29.3 +27.5 +29.9 -33.0 +42.5 -3.5 -10.7 -7.0 -12.6
Steps
(reduced) 		109
(40) 		160
(22) 		194
(56) 		219
(12) 		239
(32) 		255
(48) 		270
(63) 		282
(6) 		293
(17) 		303
(27) 		312
(36)

Intervals

Steps Cents Approximate ratios Ups and downs notation
(Dual flat fifth 40\69) 		Ups and downs notation
(Dual sharp fifth 41\69)
0 0 1/1 D D
1 17.4 ^D, vvE♭♭ ^D, vE♭
2 34.8 ^^D, vE♭♭ ^^D, E♭
3 52.2 32/31, 33/32, 34/33, 35/34 vD♯, E♭♭ ^3D, ^E♭
4 69.6 25/24, 26/25 D♯, ^E♭♭ ^4D, ^^E♭
5 87 20/19, 21/20 ^D♯, vvE♭ ^5D, ^3E♭
6 104.3 17/16, 35/33 ^^D♯, vE♭ v5D♯, ^4E♭
7 121.7 vD𝄪, E♭ v4D♯, ^5E♭
8 139.1 13/12 D𝄪, ^E♭ v3D♯, v5E
9 156.5 23/21, 34/31, 35/32 ^D𝄪, vvE vvD♯, v4E
10 173.9 21/19, 31/28, 32/29 ^^D𝄪, vE vD♯, v3E
11 191.3 19/17, 29/26 E D♯, vvE
12 208.7 26/23, 35/31 ^E, vvF♭ ^D♯, vE
13 226.1 33/29 ^^E, vF♭ E
14 243.5 23/20 vE♯, F♭ ^E, vF
15 260.9 E♯, ^F♭ F
16 278.3 20/17, 34/29 ^E♯, vvF ^F, vG♭
17 295.7 19/16 ^^E♯, vF ^^F, G♭
18 313 6/5 F ^3F, ^G♭
19 330.4 23/19, 29/24 ^F, vvG♭♭ ^4F, ^^G♭
20 347.8 ^^F, vG♭♭ ^5F, ^3G♭
21 365.2 21/17, 37/30 vF♯, G♭♭ v5F♯, ^4G♭
22 382.6 5/4 F♯, ^G♭♭ v4F♯, ^5G♭
23 400 29/23 ^F♯, vvG♭ v3F♯, v5G
24 417.4 14/11 ^^F♯, vG♭ vvF♯, v4G
25 434.8 vF𝄪, G♭ vF♯, v3G
26 452.2 13/10 F𝄪, ^G♭ F♯, vvG
27 469.6 21/16 ^F𝄪, vvG ^F♯, vG
28 487 ^^F𝄪, vG G
29 504.3 G ^G, vA♭
30 521.7 23/17 ^G, vvA♭♭ ^^G, A♭
31 539.1 ^^G, vA♭♭ ^3G, ^A♭
32 556.5 29/21 vG♯, A♭♭ ^4G, ^^A♭
33 573.9 32/23 G♯, ^A♭♭ ^5G, ^3A♭
34 591.3 31/22 ^G♯, vvA♭ v5G♯, ^4A♭
35 608.7 37/26 ^^G♯, vA♭ v4G♯, ^5A♭
36 626.1 23/16, 33/23 vG𝄪, A♭ v3G♯, v5A
37 643.5 29/20 G𝄪, ^A♭ vvG♯, v4A
38 660.9 ^G𝄪, vvA vG♯, v3A
39 678.3 34/23, 37/25 ^^G𝄪, vA G♯, vvA
40 695.7 A ^G♯, vA
41 713 ^A, vvB♭♭ A
42 730.4 29/19, 32/21, 35/23 ^^A, vB♭♭ ^A, vB♭
43 747.8 20/13, 37/24 vA♯, B♭♭ ^^A, B♭
44 765.2 A♯, ^B♭♭ ^3A, ^B♭
45 782.6 11/7 ^A♯, vvB♭ ^4A, ^^B♭
46 800 35/22 ^^A♯, vB♭ ^5A, ^3B♭
47 817.4 8/5 vA𝄪, B♭ v5A♯, ^4B♭
48 834.8 34/21 A𝄪, ^B♭ v4A♯, ^5B♭
49 852.2 ^A𝄪, vvB v3A♯, v5B
50 869.6 33/20 ^^A𝄪, vB vvA♯, v4B
51 887 5/3 B vA♯, v3B
52 904.3 32/19 ^B, vvC♭ A♯, vvB
53 921.7 17/10, 29/17 ^^B, vC♭ ^A♯, vB
54 939.1 vB♯, C♭ B
55 956.5 33/19 B♯, ^C♭ ^B, vC
56 973.9 ^B♯, vvC C
57 991.3 23/13 ^^B♯, vC ^C, vD♭
58 1008.7 34/19 C ^^C, D♭
59 1026.1 29/16 ^C, vvD♭♭ ^3C, ^D♭
60 1043.5 31/17 ^^C, vD♭♭ ^4C, ^^D♭
61 1060.9 24/13, 35/19 vC♯, D♭♭ ^5C, ^3D♭
62 1078.3 C♯, ^D♭♭ v5C♯, ^4D♭
63 1095.7 32/17 ^C♯, vvD♭ v4C♯, ^5D♭
64 1113 19/10 ^^C♯, vD♭ v3C♯, v5D
65 1130.4 25/13 vC𝄪, D♭ vvC♯, v4D
66 1147.8 31/16, 33/17 C𝄪, ^D♭ vC♯, v3D
67 1165.2 ^C𝄪, vvD C♯, vvD
68 1182.6 ^^C𝄪, vD ^C♯, vD
69 1200 2/1 D D

Proposed names

Degree Carmen's naming system Cents Approximate Ratios* Error (abs, ¢)
0 Natural Unison, 1 0.000 1/1 0.000
1 Ptolemy's comma 17.391 100/99 −0.008
2 Jubilisma, lesser septimal sixth tone 34.783 50/49, 101/99 −0.193, 0.157
3 lesser septendecimal quartertone, _____ 52.174 34/33, 101/98 0.491, −0.028
4 _____ 69.565 76/73 −0.158
5 Small undevicesimal semitone 86.957 20/19 −1.844
6 Large septendecimal semitone 104.348 17/16 −0.608
7 Septimal diatonic semitone 121.739 15/14 2.296
8 Tridecimal neutral second 139.130 13/12 0.558
9 Vicesimotertial neutral second 156.522 23/21 −0.972
10 Undevicesimal large neutral second, undevicesimal whole tone 173.913 21/19 0.645
11 Quasi-meantone 191.304 19/17 −1.253
12 Whole tone 208.696 9/8 4.786
13 Septimal whole tone 226.087 8/7 −5.087
14 Vicesimotertial semifourth 243.478 23/20 1.518
15 Subminor third, undetricesimal subminor third 260.870 7/6, 29/25 −6.001, 3.920
16 Vicesimotertial subminor third 278.261 27/23 0.670
17 Pythagorean minor third 295.652 32/27 1.517
18 Classic minor third 313.043 6/5 −2.598
19 Vicesimotertial supraminor third 330.435 23/19 −0.327
20 Undecimal neutral third 347.826 11/9 0.418
21 Septendecimal submajor third 365.217 21/17 −0.608
22 Classic major third 382.609 5/4 −3.705
23 Undetricesimal major third, Septendecimal major third 400.000 29/23, 34/27 −1.303, 0.910
24 Undecimal major third 417.391 14/11 −0.117
25 Supermajor third 434.783 9/7 −0.301
26 Barbados third 452.174 13/10 −2.040
27 Septimal sub-fourth 469.565 21/16 −1.216
28 _____ 486.957 53/40 −0.234
29 Just perfect fourth 504.348 4/3 6.303
30 Vicesimotertial acute fourth 521.739 23/17 −1.580
31 Undecimal augmented fourth 539.130 15/11 2.180
32 Undecimal superfourth, undetricesimal superfourth 556.522 11/8, 29/21 5.204, −2.275
33 Narrow tritone, classic augmented fourth 573.913 7/5, 25/18 −8.600, 5.196
34 _____ 591.304 31/22 −2.413
35 High tritone, undevicesimal tritone 608.696 10/7, 27/19 −8.792, 0.344
36 _____ 626.087 33/23 1.088
37 Undetricesimal tritone 643.478 29/20 0.215
38 Undevicesimal diminished fifth, undecimal diminished fifth 660.870 19/13, 22/15 3.884, −2.180
39 Vicesimotertial grave fifth, _____ 678.261 34/23, 37/25 1.580, −0.456
40 Just perfect fifth 695.652 3/2 −6.303
41 _____ 713.043 80/53 0.234
42 Super-fifth, undetricesimal super-fifth 730.435 32/21, 29/19 1.216, −1.630
43 Septendecimal subminor sixth 747.826 17/11 −5.811
44 Subminor sixth 765.217 14/9 0.301
45 Undecimal minor sixth 782.609 11/7 0.117
46 Septendecimal subminor sixth 800.000 27/17 −0.910
47 Classic minor sixth 817.391 8/5 3.705
48 Septendecimal supraminor sixth 834.783 34/21 0.608
49 Undecimal neutral sixth 852.174 18/11 −0.418
50 Vicesimotertial submajor sixth 869.565 38/23 0.327
51 Classic major sixth 886.957 5/3 2.598
52 Pythagorean major sixth 904.348 27/16 −1.517
53 Septendecimal major sixth, undetricesimal major sixth 921.739 17/10, 29/17 3.097, −2.883
54 Supermajor sixth, undetricesimal supermajor sixth 939.130 12/7, 50/29 6.001, −3.920
55 Vicesimotertial supermajor sixth 956.522 40/23 −1.518
56 Harmonic seventh 973.913 7/4 5.087
57 Pythagorean minor seventh 991.304 16/9 −4.786
58 Quasi-meantone minor seventh 1008.696 34/19 1.253
59 Minor neutral undevicesimal seventh 1026.087 38/21 −0.645
60 Vicesimotertial neutral seventh 1043.478 42/23 0.972
61 Tridecimal neutral seventh 1060.870 24/13 −0.558
62 Septimal diatonic major seventh 1078.261 28/15 −2.296
63 Small septendecimal major seventh 1095.652 32/17 0.608
64 Small undevicesimal semitone 1113.043 20/19 1.844
65 _____ 1130.435 73/38 0.158
66 Septendecimal supermajor seventh 1147.826 33/17 −0.491
67 _____ 1165.217 49/25 −0.193
68 _____ 1182.609 99/50 0.008
69 Octave, 8 1200.000 2/1 0.000

* Some simpler ratios listed

Notation

Ups and downs notation

Using Helmholtz–Ellis accidentals, 69edo can also be notated using ups and downs notation along with Stein–Zimmerman quarter-tone accidentals:

Step offset 0 1 2 3 4 5 6 7 8 9
Sharp symbol
 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
Flat symbol  
 		 
 
 
 
 		 

Here, a sharp raises by four steps, and a flat lowers by four steps, so arrows can be used to fill in the gap.

Sagittal notation

This notation uses the same sagittal sequence as EDOs 62 and 76.

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation1053/102433/32

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation1053/102433/32

Evo-SZ flavor

Sagittal notationPeriodic table of EDOs with sagittal notation1053/102433/32

In the diagrams above, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's primary comma (the comma it exactly represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it approximately represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this EDO.

Regular temperament properties

Subgroup Comma List Mapping Optimal
8ve Stretch (¢) 		Tuning Error
Absolute (¢) Relative (%)
2.3 [-109 69⟩ [⟨69 109]] +1.99 1.99 11.43
2.3.5 81/80, [-41 1 17⟩ [⟨69 109 160]] +1.86 1.64 9.40
2.3.5.7 81/80, 126/125, 4117715/3981312 [⟨69 109 160 193]] (69d) +2.49 1.79 10.28
2.3.5.7 81/80, 3125/3087, 6144/6125 [⟨69 109 160 194]] (69) +0.94 2.13 12.23

Rank 2 temperaments

Periods
per 8ve 		Generator Temperaments
1 2\69 Gammy (69de)
1 19\69 Rarity
1 20\69 Mohaha (69e)
1 22\69 Caleb (69)
marveltri (69)
1 29\69 Meantone (69d)
3 5\69 Ogene (69bceef)
3 6\69 August (7-limit, 69cdd)
Lithium (69)
3 9\69 Nessafof (69e)

Scales

  • Supermajor[11], 3L 8s – 6 6 6 7 6 6 6 7 6 6 7
  • Meantone[7], 5L 2s (gen = 40\69) – 11 11 7 11 11 11 7
  • Meantone[12], 7L 5s (gen = 40\69) – 7 4 7 4 7 4 7 7 4 7 4 7
  • Lithium[9], 3L 6s – 11 6 6 11 6 6 11 6 6
  • Lithium[12], 9L 3s – 5 6 6 6 5 6 6 6 5 6 6 6

Music

Eliora
Francium
Retrieved from "https://en.xen.wiki/index.php?title=69edo&oldid=181840"