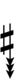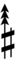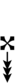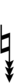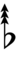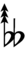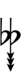61edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
m Cleanup
+intro to the tuning profile, as a compensation for the removal of the poem
 
(33 intermediate revisions by 14 users not shown)
Line 1: Line 1:
'''61edo''' refers to the equal division of [[2/1]] ratio into 61 equal parts, of 19.6721 [[cent]]s each.
{{Infobox ET}}
{{ED intro}}


61edo is the 18th [[prime numbers|prime]] EDO, after of [[59edo]] and before of [[67edo]]. It provides the [[optimal patent val]] for the 24&37 temperament in the 7-, 11- and 13-limit.
== Theory ==
61edo is only [[consistent]] to the [[5-odd-limit]]. Its [[3/1|3rd]] and [[5/1|5th]] [[harmonic]]s are sharp of just by more than 6 cents, and the [[7/1|7th]] and [[11/1|11th]], though they err by less, are on the flat side. This limits its harmonic inventory. However, it does possess reasonably good approximations of [[21/16]] and [[23/16]], only a bit more than one cent off in each case.  


== Poem ==
As an equal temperament, 61et is characterized by [[tempering out]] 20000/19683 ([[tetracot comma]]) and 262144/253125 ([[passion comma]]) in the 5-limit. In the 7-limit, the [[patent val]] {{val| 61 97 142 '''171''' }} [[support]]s [[valentine]] ({{nowrap| 15 & 46 }}), and is the [[optimal patent val]] for [[freivald]] ({{nowrap| 24 & 37 }}) in the 7-, 11- and 13-limit. The 61d [[val]] {{val| 61 97 142 '''172''' }} is a great tuning for [[modus]] and [[quasisuper]], and is a simple but out-of-tune edo tuning for [[parakleismic]].
These 61 equal divisions of the octave,


though rare are assuredly a ROCK-tave (har har),
=== Odd harmonics ===
{{Harmonics in equal|61}}


while the 3rd and 5th harmonics are about six cents sharp,
=== Subsets and supersets ===
61edo is the 18th [[prime edo]], after [[59edo]] and before [[67edo]]. [[183edo]], which triples it, corrects its approximation to many of the lower harmonics.


(and the flattish 15th poised differently on the harp),
== Intervals ==
{{Interval table}}


the 7th and 11th err by less, around three,
== Notation ==
=== Ups and downs notation ===
61edo can be notated using [[ups and downs notation]] using [[Helmholtz–Ellis]] accidentals:


and thus mayhap, a good orgone tuning found to be;
{{Sharpness-sharp8}}


slightly sharp as well, is the 13th harmonic's place,
=== Sagittal notation ===
This notation uses the same sagittal sequence as [[54edo #Sagittal notation|54edo]].


but the 9th and 17th lack near so much grace,
==== Evo flavor ====
<imagemap>
File:61-EDO_Evo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 704 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 140 106 [[513/512]]
rect 140 80 240 106 [[81/80]]
rect 240 80 360 106 [[33/32]]
rect 360 80 480 106 [[27/26]]
default [[File:61-EDO_Evo_Sagittal.svg]]
</imagemap>


interestingly the 19th is good but a couple cents flat,
==== Revo flavor ====
<imagemap>
File:61-EDO_Revo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 650 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 140 106 [[513/512]]
rect 140 80 240 106 [[81/80]]
rect 240 80 360 106 [[33/32]]
rect 360 80 480 106 [[27/26]]
default [[File:61-EDO_Revo_Sagittal.svg]]
</imagemap>


and the 21st and 23rd are but a cent or two sharp!
==== Evo-SZ flavor ====
<imagemap>
File:61-EDO_Evo-SZ_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 696 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 140 106 [[513/512]]
rect 140 80 240 106 [[81/80]]
rect 240 80 360 106 [[33/32]]
rect 360 80 480 106 [[27/26]]
default [[File:61-EDO_Evo-SZ_Sagittal.svg]]
</imagemap>


== Intervals ==
In the diagrams above, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's [[Sagittal notation#Primary comma|primary comma]] (the comma it ''exactly'' represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it ''approximately'' represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this edo.


{| class="wikitable center-1 right-2"
== Regular temperament properties ==
{| class="wikitable center-4 center-5 center-6"
|-
|-
! #
! rowspan="2" |[[Subgroup]]
! Cents
! rowspan="2" |[[Comma list]]
! rowspan="2" |[[Mapping]]
! rowspan="2" | Optimal<br>8ve stretch (¢)
! colspan="2" | Tuning error
|-
|-
| 0
![[TE error|Absolute]] (¢)
| 0.000
![[TE simple badness|Relative]] (%)
|-
|-
| 1
| 2.3
| 19.672
|{{Monzo| 97 -61 }}
|{{Mapping| 61 97 }}
| −1.97
| 1.97
| 10.0
|-
|-
| 2
| 2.3.5
| 39.344
| 20000/19683, 262144/253125
|{{Mapping| 61 97 142 }}
| −2.33
| 1.69
| 8.59
|- style="border-top: double;"
| 2.3.5.7
| 64/63, 2430/2401, 3125/3087
|{{mapping| 61 97 142 172 }} (61d)
| −3.06
| 1.93
| 9.84
|- style="border-top: double;"
| 2.3.5.7
| 126/125, 1029/1024, 2240/2187
|{{Mapping| 61 97 142 171 }} (61)
| −1.32
| 2.29
| 11.7
|}
 
=== Rank-2 temperaments ===
{| class="wikitable center-all left-5"
|+ style="font-size: 105%;" |Table of rank-2 temperaments by generator
|-
|-
| 3
! Periods<br>per 8ve
| 59.016
! Generator*
! Cents*
! Associated<br>ratio*
! Temperament
|-
|-
| 4
| 1
| 78.689
| 2\61
| 39.3
| 40/39
|[[Hemivalentine]] (61)
|-
|-
| 5
| 1
| 98.361
| 3\61
| 59.0
| 28/27
|[[Dodecacot]] (61de…)
|-
|-
| 6
| 1
| 118.033
| 4\61
| 78.7
| 22/21
|[[Valentine]] (61)
|-
|-
| 7
| 1
| 137.705
| 5\61
| 98.4
| 16/15
|[[Passion]] (61de…) / [[passionate]] (61)
|-
|-
| 8
| 1
| 157.377
| 7\61
| 137.7
| 13/12
|[[Quartemka]] (61)
|-
|-
| 9
| 1
| 177.049
| 9\61
| 177.0
| 10/9
|[[Modus]] (61de) / [[wollemia]] (61e)
|-
|-
| 10
| 1
| 196.721
| 11\61
| 236.1
| 8/7
|[[Slendric]] (61)
|-
|-
| 11
| 1
| 216.393
| 16\61
| 314.8
| 6/5
|[[Parakleismic]] (61d)
|-
|-
| 12
| 1
| 236.066
| 23\61
| 452.5
| 13/10
|[[Maja]] (61d)
|-
|-
| 13
| 1
| 255.738
| 25\61
| 491.8
| 4/3
|[[Quasisuper]] (61d)
|-
|-
| 14
| 1
| 275.410
| 28\61
|-
| 550.8
| 15
| 11/8
| 295.082
|[[Freivald]] (61)
|-
| 16
| 314.754
|-
| 17
| 334.426
|-
| 18
| 354.098
|-
| 19
| 373.770
|-
| 20
| 393.443
|-
| 21
| 413.115
|-
| 22
| 432.787
|-
| 23
| 452.459
|-
| 24
| 472.131
|-
| 25
| 491.803
|-
| 26
| 511.475
|-
| 27
| 531.148
|-
| 28
| 550.820
|-
| 29
| 570.492
|-
| 30
| 590.164
|-
| 31
| 609.836
|-
| 32
| 629.508
|-
| 33
| 649.180
|-
| 34
| 668.852
|-
| 35
| 688.525
|-
| 36
| 708.197
|-
| 37
| 727.869
|-
| 38
| 747.541
|-
| 39
| 767.213
|-
| 40
| 786.885
|-
| 41
| 806.557
|-
| 42
| 826.230
|-
| 43
| 845.902
|-
| 44
| 865.574
|-
| 45
| 885.246
|-
| 46
| 904.918
|-
| 47
| 924.590
|-
| 48
| 944.262
|-
| 49
| 963.934
|-
| 50
| 983.607
|-
| 51
| 1003.279
|-
| 52
| 1022.951
|-
| 53
| 1042.623
|-
| 54
| 1062.295
|-
| 55
| 1081.967
|-
| 56
| 1101.639
|-
| 57
| 1121.311
|-
| 58
| 1140.984
|-
| 59
| 1160.656
|-
| 60
| 1180.328
|-
| 61
| 1200.000
|}
|}
<nowiki/>* [[Normal lists|Octave-reduced form]], reduced to the first half-octave
== Instruments ==
A [[Lumatone mapping for 61edo]] has now been demonstrated (see the Valentine mapping for full gamut coverage).
== See also ==


[[Category:Equal divisions of the octave]]
=== Introductory poem ===
[[Category:Prime EDO]]
[[Peter Kosmorsky]] wrote a poem on 61edo; see [[User:Spt3125/61edo poem|the 61edo poem]].


[[Category:Todo:add sound example]]
== Music ==
; [[Bryan Deister]]
* [https://www.youtube.com/shorts/1Ai__APev5M ''microtonal improvisation in 61edo''] (2025)

Latest revision as of 11:36, 11 April 2025

← 60edo 61edo 62edo →
Prime factorization 61 (prime)
Step size 19.6721 ¢ 
Fifth 36\61 (708.197 ¢)
Semitones (A1:m2) 8:3 (157.4 ¢ : 59.02 ¢)
Consistency limit 5
Distinct consistency limit 5

61 equal divisions of the octave (abbreviated 61edo or 61ed2), also called 61-tone equal temperament (61tet) or 61 equal temperament (61et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 61 equal parts of about 19.7 ¢ each. Each step represents a frequency ratio of 21/61, or the 61st root of 2.

Theory

61edo is only consistent to the 5-odd-limit. Its 3rd and 5th harmonics are sharp of just by more than 6 cents, and the 7th and 11th, though they err by less, are on the flat side. This limits its harmonic inventory. However, it does possess reasonably good approximations of 21/16 and 23/16, only a bit more than one cent off in each case.

As an equal temperament, 61et is characterized by tempering out 20000/19683 (tetracot comma) and 262144/253125 (passion comma) in the 5-limit. In the 7-limit, the patent val ⟨61 97 142 171] supports valentine (15 & 46), and is the optimal patent val for freivald (24 & 37) in the 7-, 11- and 13-limit. The 61d val ⟨61 97 142 172] is a great tuning for modus and quasisuper, and is a simple but out-of-tune edo tuning for parakleismic.

Odd harmonics

Approximation of odd harmonics in 61edo
Harmonic 3 5 7 9 11 13 15 17 19 21 23
Error Absolute (¢) +6.24 +7.13 -4.89 -7.19 -0.50 +5.37 -6.30 -6.59 -2.43 +1.35 +1.23
Relative (%) +31.7 +36.2 -24.9 -36.5 -2.5 +27.3 -32.0 -33.5 -12.4 +6.9 +6.3
Steps
(reduced) 		97
(36) 		142
(20) 		171
(49) 		193
(10) 		211
(28) 		226
(43) 		238
(55) 		249
(5) 		259
(15) 		268
(24) 		276
(32)

Subsets and supersets

61edo is the 18th prime edo, after 59edo and before 67edo. 183edo, which triples it, corrects its approximation to many of the lower harmonics.

Intervals

Steps Cents Approximate ratios Ups and downs notation
0 0 1/1 D
1 19.7 ^D, vvE♭
2 39.3 ^^D, vE♭
3 59 29/28, 32/31 ^3D, E♭
4 78.7 22/21, 23/22 ^4D, ^E♭
5 98.4 35/33 v3D♯, ^^E♭
6 118 31/29 vvD♯, ^3E♭
7 137.7 13/12 vD♯, v4E
8 157.4 23/21, 34/31, 35/32 D♯, v3E
9 177 21/19, 31/28 ^D♯, vvE
10 196.7 19/17 ^^D♯, vE
11 216.4 26/23 E
12 236.1 ^E, vvF
13 255.7 22/19 ^^E, vF
14 275.4 34/29 F
15 295.1 19/16 ^F, vvG♭
16 314.8 6/5 ^^F, vG♭
17 334.4 17/14, 23/19 ^3F, G♭
18 354.1 ^4F, ^G♭
19 373.8 26/21 v3F♯, ^^G♭
20 393.4 vvF♯, ^3G♭
21 413.1 14/11, 33/26 vF♯, v4G
22 432.8 F♯, v3G
23 452.5 13/10 ^F♯, vvG
24 472.1 21/16 ^^F♯, vG
25 491.8 G
26 511.5 35/26 ^G, vvA♭
27 531.1 19/14 ^^G, vA♭
28 550.8 11/8 ^3G, A♭
29 570.5 25/18, 32/23 ^4G, ^A♭
30 590.2 31/22 v3G♯, ^^A♭
31 609.8 vvG♯, ^3A♭
32 629.5 23/16 vG♯, v4A
33 649.2 16/11, 35/24 G♯, v3A
34 668.9 28/19 ^G♯, vvA
35 688.5 ^^G♯, vA
36 708.2 A
37 727.9 29/19, 32/21, 35/23 ^A, vvB♭
38 747.5 20/13 ^^A, vB♭
39 767.2 ^3A, B♭
40 786.9 11/7 ^4A, ^B♭
41 806.6 35/22 v3A♯, ^^B♭
42 826.2 21/13 vvA♯, ^3B♭
43 845.9 31/19 vA♯, v4B
44 865.6 28/17, 33/20 A♯, v3B
45 885.2 5/3 ^A♯, vvB
46 904.9 32/19 ^^A♯, vB
47 924.6 29/17 B
48 944.3 19/11 ^B, vvC
49 963.9 ^^B, vC
50 983.6 23/13 C
51 1003.3 34/19 ^C, vvD♭
52 1023 ^^C, vD♭
53 1042.6 31/17 ^3C, D♭
54 1062.3 24/13 ^4C, ^D♭
55 1082 v3C♯, ^^D♭
56 1101.6 vvC♯, ^3D♭
57 1121.3 21/11 vC♯, v4D
58 1141 31/16 C♯, v3D
59 1160.7 ^C♯, vvD
60 1180.3 ^^C♯, vD
61 1200 2/1 D

Notation

Ups and downs notation

61edo can be notated using ups and downs notation using Helmholtz–Ellis accidentals:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
Sharp symbol  
Flat symbol

Sagittal notation

This notation uses the same sagittal sequence as 54edo.

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation513/51281/8033/3227/26

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation513/51281/8033/3227/26

Evo-SZ flavor

Sagittal notationPeriodic table of EDOs with sagittal notation513/51281/8033/3227/26

In the diagrams above, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's primary comma (the comma it exactly represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it approximately represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this edo.

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3 [97 -61⟩ [⟨61 97]] −1.97 1.97 10.0
2.3.5 20000/19683, 262144/253125 [⟨61 97 142]] −2.33 1.69 8.59
2.3.5.7 64/63, 2430/2401, 3125/3087 [⟨61 97 142 172]] (61d) −3.06 1.93 9.84
2.3.5.7 126/125, 1029/1024, 2240/2187 [⟨61 97 142 171]] (61) −1.32 2.29 11.7

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods
per 8ve 		Generator* Cents* Associated
ratio* 		Temperament
1 2\61 39.3 40/39 Hemivalentine (61)
1 3\61 59.0 28/27 Dodecacot (61de…)
1 4\61 78.7 22/21 Valentine (61)
1 5\61 98.4 16/15 Passion (61de…) / passionate (61)
1 7\61 137.7 13/12 Quartemka (61)
1 9\61 177.0 10/9 Modus (61de) / wollemia (61e)
1 11\61 236.1 8/7 Slendric (61)
1 16\61 314.8 6/5 Parakleismic (61d)
1 23\61 452.5 13/10 Maja (61d)
1 25\61 491.8 4/3 Quasisuper (61d)
1 28\61 550.8 11/8 Freivald (61)

* Octave-reduced form, reduced to the first half-octave

Instruments

A Lumatone mapping for 61edo has now been demonstrated (see the Valentine mapping for full gamut coverage).

See also

Introductory poem

Peter Kosmorsky wrote a poem on 61edo; see the 61edo poem.

Music

Bryan Deister
Retrieved from "https://en.xen.wiki/index.php?title=61edo&oldid=191167"