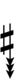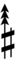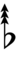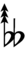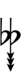42edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
Dave Keenan (talk | contribs)
autopatrolled, emailconfirmed
1,671 edits
→Notation: added Sagittal notation
BudjarnLambeth (talk | contribs)
autopatrolled, emailconfirmed
18,768 edits
Stretch compression
 
(25 intermediate revisions by 7 users not shown)
Line 1: Line 1:
{{Infobox ET}}
{{Infobox ET}}
{{EDO intro|42}}
{{ED intro}}


== Theory ==
== Theory ==
Line 7: Line 7:
42edo is on the [[optimal ET sequence]] of the [[Augmented family#eugene|eugene]], [[joan]], [[lemba]], [[neutron]], [[qeema]], [[seville]], [[sevond]], [[skateboard]], [[tritikleismic]] and [[vines]] temperaments.
42edo is on the [[optimal ET sequence]] of the [[Augmented family#eugene|eugene]], [[joan]], [[lemba]], [[neutron]], [[qeema]], [[seville]], [[sevond]], [[skateboard]], [[tritikleismic]] and [[vines]] temperaments.


42edo is a diatonic edo because its 5th falls between 4\7 = 686¢ and 3\5 = 720¢. 42edo is one of the most difficult diatonic edos to notate, because no other diatonic edo's 5th is as sharp (see [[47edo]] for the opposite extreme).  
42edo is a diatonic edo because its 5th falls between {{nowrap|4\7 {{=}} 686{{c}}}} and {{nowrap|3\5 {{=}} 720{{c}}}}. 42edo is one of the most difficult diatonic edos to notate, because no other diatonic edo's fifth is as sharp (see [[47edo]] for the opposite extreme).  


=== Odd harmonics ===
=== Odd harmonics ===
While not an accurate tuning on the full [[7-limit]], 42edo does an excellent job on the 2.9.15.7.33.39 [[k*N subgroups|2*42 subgroup]], having the same tuning on it as does [[84edo]]. On this subgroup 42 has the same [[comma]]s as 84.
While not an accurate tuning on the full [[7-limit]], 42edo does an excellent job on the 2.9.15.7.33.39 [[k*N subgroups|2*42 subgroup]], having the same tuning on it as does [[84edo]]. On this subgroup 42 has the same [[comma]]s as 84.
{{Harmonics in equal|42}}
{{Harmonics in equal|42}}
=== Octave stretch ===
42edo’s inaccurate 3rd and 5th harmonics can be greatly improved through [[octave stretching]] or [[octave shrinking]]. Both approaches work about equally well but in opposite directions, giving two quite different flavors of tuning to play with.
The following table compares three stretched tunings of 42edo:
{| class="wikitable"
|+
!Tuning
! [[42ed257/128]]
! [[1ed28.7c|APS720jot]]
! [[zpi|189zpi]]
! [[42edo]]
|-
! Steps / octave
| ~41.77
| ~41.81
| ~41.83
| 42.00
|-
! Approximation <br>of harmonics
| great: 5 <br>good: 2, 3, 7 <br>okay: <br>bad: 11, 13
| great: 5 <br>good: 2, 3 <br>okay: 7, 11, 13 <br>bad:
| great: 5 <br>good: 2, 13 <br>okay: 3, 11 <br>bad: 7
| great: 2, 7 <br>good: <br>okay: 11 <br>bad: 3, 5, 13
|-
| colspan="5" | <small><div style="text-align: center;">''“great” = 0-13% relative error • “good” = 13-27% • “okay” = 27-40% • “bad” = 40-50%''</div></small>
|}
The following table compares three compressed tunings of 42edo:
{| class="wikitable"
|+
!Tuning
! [[42edo]]
! [[1ed28.5c|APS715jot]]
! [[191zpi]]
! [[ed255/128#42ed255/128|42ed255/128]]
|-
! Steps / octave
| 42.00
| ~42.10
| ~42.19
| ~42.24
|-
! Approximation <br>of harmonics
| great: 2, 7 <br>good: <br>okay: 11 <br>bad: 3, 5, 13
| great: 2 <br>good: 5, 7, 13 <br>okay: 3, 11 <br>bad:
| great: 5, 11, 13 <br>good: 2, 3 <br>okay: <br>bad: 7
| great: 3, 5, 11 <br>good: 2 <br>okay: 13 <br>bad: 7
|-
| colspan="5" | <small><div style="text-align: center;">''“great” = 0-13% relative error • “good” = 13-27% • “okay” = 27-40% • “bad” = 40-50%''</div></small>
|}
For a more detailed comparison see [[Table of stretched 42edo tunings]].


=== Subsets and supersets ===
=== Subsets and supersets ===
Since 42 factors into {{factorization|42}}, 42edo contains subset edos {{EDOs| 2, 3, 6, 7, 14, and 21 }}.
Since 42 factors into {{factorization|42}}, 42edo contains subset edos {{EDOs| 2, 3, 6, 7, 14, and 21 }}.


==Intervals==
== Intervals ==
 
{| class="wikitable center-all right-2 left-4"
{| class="wikitable center-all right-2 left-4"
|-
|-
!#
! #
!Cents
! Cents
! colspan="3" |[[Ups and Downs Notation]]
! colspan="3" | [[Ups and downs notation]]
|-
|-
|0
| 0
| 0.000
| 0.0
|P1
| P1
|perfect unison
| perfect unison
| D
| D
|-
|-
|1
| 1
|28.571
| 28.6
|^1, m2
| ^1, m2
| up unison, minor 2nd
| up unison, minor 2nd
|^D, Eb
| ^D, Eb
|-
|-
|2
| 2
|57.143
| 57.1
|^^1, ^m2
| ^^1, ^m2
|dup 1sn, upminor 2nd
| dup 1sn, upminor 2nd
| ^^D, ^Eb
| ^^D, ^Eb
|-
|-
|3
| 3
|85.714
| 85.7
|^^m2
| ^^m2
|dupminor 2nd
| dupminor 2nd
|^^Eb
| ^^Eb
|-
|-
| 4
| 4
|114.286
| 114.3
|^<sup>3</sup>m
| ^<sup>3</sup>m
|trupminor 2nd
| trupminor 2nd
|^<sup>3</sup>Eb
| ^<sup>3</sup>Eb
|-
|-
|5
| 5
|143.857
| 143.9
|v<sup>3</sup>M
| v<sup>3</sup>M
|trudmajor 2nd
| trudmajor 2nd
|v<sup>3</sup>E
| v<sup>3</sup>E
|-
|-
|6
| 6
|171.429
| 171.4
|vvM2
| vvM2
| dudmajor 2nd
| dudmajor 2nd
|vvE
| vvE
|-
|-
|7
| 7
|200.000
| 200.0
|vM2
| vM2
|downmajor 2nd
| downmajor 2nd
|vE
| vE
|-
|-
| 8
| 8
|228.571
| 228.6
|M2
| M2
|major 2nd
| major 2nd
| E
| E
|-
|-
|9
| 9
|257.143
| 257.1
|m3
| m3
|minor 3rd
| minor 3rd
|F
| F
|-
|-
|10
| 10
| 285.714
| 285.7
|^m3
| ^m3
| upminor 3rd
| upminor 3rd
|^F
| ^F
|-
|-
|11
| 11
|314.286
| 314.3
|^^m3
| ^^m3
|dupminor 3rd
| dupminor 3rd
|^^F
| ^^F
|-
|-
|12
| 12
|342.857
| 342.9
|^<sup>3</sup>m3
| ^<sup>3</sup>m3
| trupminor 3rd
| trupminor 3rd
|^<sup>3</sup>F
| ^<sup>3</sup>F
|-
|-
|13
| 13
|371.429
| 371.4
|v<sup>3</sup>M3
| v<sup>3</sup>M3
|trudmajor 3rd
| trudmajor 3rd
|v<sup>3</sup>F#
| v<sup>3</sup>F#
|-
|-
|14
| 14
|400.000
| 400.0
|vvM3
| vvM3
|dudmajor 3rd
| dudmajor 3rd
|vvF#
| vvF#
|-
|-
|15
| 15
|428.571
| 428.6
|vM3
| vM3
|downmajor 3rd
| downmajor 3rd
| vF#
| vF#
|-
|-
|16
| 16
| 457.143
| 457.1
|M3, v4
| M3, v4
|major 3rd, down 4th
| major 3rd, down 4th
|F#, vG
| F#, vG
|-
|-
| 17
| 17
|485.714
| 485.7
|P4
| P4
|perfect 4th
| perfect 4th
|G
| G
|-
|-
|18
| 18
| 514.286
| 514.3
|^4
| ^4
|up 4th
| up 4th
|^G
| ^G
|-
|-
|19
| 19
|543.857
| 543.9
| ^^4
| ^^4
|dup 4th
| dup 4th
|^^G
| ^^G
|-
|-
|20
| 20
|571.429
| 571.4
|^<sup>3</sup>4, ^^d5
| ^<sup>3</sup>4, ^^d5
| trup 4th, dupdim 5th
| trup 4th, dupdim 5th
| ^<sup>3</sup>G, ^^Ab
| ^<sup>3</sup>G, ^^Ab
|-
|-
|21
| 21
|600.000
| 600.0
|v<sup>3</sup>A4, ^<sup>3</sup>d5
| v<sup>3</sup>A4, ^<sup>3</sup>d5
|trudaug 4th, trupdim 5th
| trudaug 4th, trupdim 5th
|v<sup>3</sup>G#, ^<sup>3</sup>Ab
| v<sup>3</sup>G#, ^<sup>3</sup>Ab
|-
|-
|22
| 22
|628.571
| 628.6
|vvA4, v<sup>3</sup>5
| vvA4, v<sup>3</sup>5
|dudaug 4th, trud 5th
| dudaug 4th, trud 5th
|vvG#, v<sup>3</sup>A
| vvG#, v<sup>3</sup>A
|-
|-
|23
| 23
|657.143
| 657.1
|vv5
| vv5
|dud 5th
| dud 5th
|vvA
| vvA
|-
|-
|24
| 24
| 685.714
| 685.7
|v5
| v5
|down 5th
| down 5th
| vA
| vA
|-
|-
|25
| 25
|714.286
| 714.3
|P5
| P5
|perfect 5th
| perfect 5th
|A
| A
|-
|-
|26
| 26
|742.857
| 742.9
|^5, m6
| ^5, m6
|up 5th, minor 6th
| up 5th, minor 6th
|^A, Bb
| ^A, Bb
|-
|-
|27
| 27
|771.429
| 771.4
|^m6
| ^m6
|upminor 6th
| upminor 6th
|^Bb
| ^Bb
|-
|-
|28
| 28
|800.000
| 800.0
|^^m6
| ^^m6
|dupminor 6th
| dupminor 6th
|^^Bb
| ^^Bb
|-
|-
|29
| 29
|828.571
| 828.6
|^<sup>3</sup>m6
| ^<sup>3</sup>m6
| trupminor 6th
| trupminor 6th
| ^<sup>3</sup>Bb
| ^<sup>3</sup>Bb
|-
|-
|30
| 30
|857.143
| 857.1
|v<sup>3</sup>M6
| v<sup>3</sup>M6
|trudmajor 6th
| trudmajor 6th
|v<sup>3</sup>B
| v<sup>3</sup>B
|-
|-
| 31
| 31
|885.714
| 885.7
|vvM6
| vvM6
|dudmajor 6th
| dudmajor 6th
|vvB
| vvB
|-
|-
|32
| 32
|914.286
| 914.3
|vM6
| vM6
|downmajor 6th
| downmajor 6th
|vB
| vB
|-
|-
|33
| 33
|942.857
| 942.9
|M6
| M6
|major 6th
| major 6th
|B
| B
|-
|-
| 34
| 34
|971.429
| 971.4
|m7
| m7
|minor 7th
| minor 7th
|C
| C
|-
|-
|35
| 35
|1000.000
| 1000.0
|^m7
| ^m7
|upminor 7th
| upminor 7th
|^C
| ^C
|-
|-
|36
| 36
|1028.571
| 1028.6
|^^m7
| ^^m7
| dupminor 7th
| dupminor 7th
|^^C
| ^^C
|-
|-
|37
| 37
|1057.143
| 1057.1
|^<sup>3</sup>m7
| ^<sup>3</sup>m7
|trupminor 7th
| trupminor 7th
|^<sup>3</sup>C
| ^<sup>3</sup>C
|-
|-
|38
| 38
|1085.714
| 1085.7
|v<sup>3</sup>M7
| v<sup>3</sup>M7
|trudmajor 7th
| trudmajor 7th
| v<sup>3</sup>C#
| v<sup>3</sup>C#
|-
|-
|39
| 39
| 1114.286
| 1114.3
|vvM7
| vvM7
|dudmajor 7th
| dudmajor 7th
| vvC#
| vvC#
|-
|-
|40
| 40
|1142.857
| 1142.9
|vM7
| vM7
|downmajor 7th
| downmajor 7th
|vC#
| vC#
|-
|-
|41
| 41
| 1171.429
| 1171.4
|M7, v8
| M7, v8
|major 7th, down 8ve
| major 7th, down 8ve
|C#, vD
| C#, vD
|-
|-
|42
| 42
| 1200.000
| 1200.0
|P8
| P8
| perfect 8ve
| perfect 8ve
|D
| D
|}
|}


Chords can be named using ups and downs as C upminor, D downmajor seven, etc. See [[Ups and Downs Notation #Chords and Chord Progressions]].
Chords can be named using ups and downs as C upminor, D downmajor seven, etc. See [[Ups and downs notation #Chords and chord progressions]].


==Notation==
== Notation ==
=== Ups and downs notation ===
=== Ups and downs notation ===
Assuming the natural notes form a [[chain of fifths]], the major 2nd is 8 edosteps and the minor 2nd is only one. The naturals create a [[5edo]]-like scale, with two of the notes inflected by a [[comma]]-sized edostep:
Assuming the natural notes form a [[chain of fifths]], the major 2nd is 8 edosteps and the minor 2nd is only one. The naturals create a [[5edo]]-like scale, with two of the notes inflected by a [[comma]]-sized edostep:


D * * * * * * * * E F * * * * * * * * G * * * * * * * * A * * * * * * * * B C * * * * * * * * D
D * * * * * * * E F * * * * * * * G * * * * * * * A * * * * * * * B C * * * * * * * D
 
D♯ is next to E. The notation requires ups and downs with three arrows, and if chords are to be spelled correctly four or more arrows may be required in certain cases. For example, a {{dash|1/1, 5/4, 3/2, 9/5|med}} chord with a root on the edostep midway between G and A would be written either as {{dash|v<sup>3</sup>G♯–v<sup>5</sup>B♯, v<sup>3</sup>D♯, vF♯|med}} or as {{dash|^<sup>3</sup>A♭, ^C, ^<sup>3</sup>E♭, ^<sup>5</sup>G♭}}. This is a dud dup-seven chord, written either as v<sup>3</sup>G♯vv,^^7 or as ^<sup>3</sup>A♭vv,^^7.


D# is next to E. The notation requires triple ups and downs, even more if chords are to be spelled correctly. For example, a 1/1 - 5/4 - 3/2 - 9/5 chord with a root on the key or fret midway between G and A would be written either as v<sup>3</sup>G# - v<sup>5</sup>B# - v<sup>3</sup>D# - vF# or as ^<sup>3</sup>Ab - ^C - ^<sup>3</sup>Eb - ^<sup>5</sup>Gb. This is a dud dup-seven chord, written either as v<sup>3</sup>G#vv,^^7 or as ^<sup>3</sup>Abvv,^^7.
In this table, dup is equivalent to quidsharp, trup is equivalent to quudsharp, trudsharp is equivalent to quup, dudsharp is equivalent to quip, etc.
{{sharpness-sharp7a}}


===Sagittal notation===
Alternatively, sharps and flats with arrows borrowed from [[Helmholtz–Ellis notation]] can be used:
====Best fifth notation====
This notation uses the same sagittal sequence as [[35edo#Second-best fifth notation|35b]].
=====Evo flavor=====


{{sharpness-sharp7}}
=== Sagittal notation ===
==== Best fifth notation ====
This notation uses the same sagittal sequence as [[35edo #Second-best fifth notation|35b]].
===== Evo flavor =====
<imagemap>
<imagemap>
File:42-EDO_Evo_Sagittal.svg
File:42-EDO_Evo_Sagittal.svg
Line 362: Line 314:
</imagemap>
</imagemap>


=====Revo flavor=====
===== Revo flavor =====
 
<imagemap>
<imagemap>
File:42-EDO_Revo_Sagittal.svg
File:42-EDO_Revo_Sagittal.svg
Line 373: Line 324:
</imagemap>
</imagemap>


====Second-best fifth notation====
==== Second-best fifth notation ====
This notation uses the same sagittal sequence as [[47edo#Sagittal notation|47-EDO]], and is a superset of the notations for EDOs [[21edo#Sagittal notation|21]], [[14edo#Sagittal notation|14]], and [[7edo#Sagittal notation|7]].
This notation uses the same sagittal sequence as [[47edo#Sagittal notation|47edo]], and is a superset of the notations for edos [[21edo #Sagittal notation|21]], [[14edo #Sagittal notation|14]], and [[7edo #Sagittal notation|7]].


<imagemap>
<imagemap>
Line 385: Line 336:
</imagemap>
</imagemap>


==Scales==
== Approximation to JI ==
{{Q-odd-limit intervals}}
 
== Regular temperament properties ==
{| class="wikitable center-4 center-5 center-6"
|-
! rowspan="2" | [[Subgroup]]
! rowspan="2" | [[Comma list]]
! rowspan="2" | [[Mapping]]
! rowspan="2" | Optimal<br>8ve stretch (¢)
! colspan="2" | Tuning error
|-
! [[TE error|Absolute]] (¢)
! [[TE simple badness|Relative]] (%)
|-
| 2.3
| {{Monzo| 67 -42 }}
| {{Mapping| 42 67 }}
| −3.89
| 3.88
| 13.57
|-
| 2.3.5
| 128/125, 5000000/4782969
| {{Mapping| 42 67 98 }}
| −4.55
| 3.30
| 11.55
|-
| 2.3.5.7
| 64/63, 126/125, 6860/6561
| {{Mapping| 42 67 98 118 }}
| −3.65
| 3.26
| 11.42
|}
 
== Octave stretch or compression ==
42edo’s inaccurate 3rd and 5th harmonics can be greatly improved through [[stretched and compressed tuning|stretching or compressing]] octaves. Both approaches work about equally well but in opposite directions, giving two quite different flavors of tuning to play with.
 
What follows is a comparison of stretched- and compressed-octave 42edo tunings.
 
; [[ed6|108ed6]]
* Octave size: 1206.3{{c}}
Stretching the octave of 42edo by around 6{{c}} results in improved primes 3, 5 and 13, but worse primes 2, 7 and 11. This approximates all harmonics up to 16 within 13.3{{c}}. The tuning 108ed6 does this. So does the tuning [[ed5|97ed5]] whose octave differs by only 0.1{{c}}.
{{Harmonics in equal|108|6|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 108ed6}}
{{Harmonics in equal|108|6|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 108ed6 (continued)}}
 
; [[zpi|189zpi]]
* Step size: 28.689{{c}}, octave size: 1204.9{{c}}
Stretching the octave of 42edo by around 5{{c}} results in improved primes 3, 5 and 13, but worse primes 2 and 11. This approximates all harmonics up to 16 within 13.9{{c}}. The tuning 189zpi does this.
{{Harmonics in cet|28.689|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 189zpi}}
{{Harmonics in cet|28.689|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 189zpi (continued)}}
 
; [[ed12|150ed12]]
* Octave size: 1204.5{{c}}
Stretcing the octave of 42edo by around 4.5{{c}} results in improved primes 3, 5, 11 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 13.6{{c}}. The tuning 150ed12 does this.
{{Harmonics in equal|150|12|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 150ed12}}
{{Harmonics in equal|150|12|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 150ed12 (continued)}}
 
; [[equal tuning|145ed11]]
* Octave size: 1202.5{{c}}
Stretching the octave of 42edo by around 2.5{{c}} results in improved primes 5, 11 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 11.9{{c}}. The tuning 145ed11 does this.
{{Harmonics in equal|145|11|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 145ed11}}
{{Harmonics in equal|145|11|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 145ed11 (continued)}}
 
; 42edo
* Step size: 28.571{{c}}, octave size: 1200.0{{c}}
Pure-octaves 42edo approximates all harmonics up to 16 within 13.7{{c}}. The tuning [[zpi|190zpi]] is almost exactly the same as pure-octaves 42edo, its octave differing by less than 0.05{{c}}.
{{Harmonics in equal|42|2|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 42edo}}
{{Harmonics in equal|42|2|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 42edo (continued)}}
 
; [[ed7|118ed7]]
* Step size: Octave size: 1199.1{{c}}
Compressing the octave of 42edo by around 1{{c}} results in improved primes 3, 5 and 7, but worse primes 2, 11 and 13. This approximates all harmonics up to 16 within 13.2{{c}}. The tuning 118ed7 does this.
{{Harmonics in equal|118|7|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 118ed7}}
{{Harmonics in equal|118|7|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 118ed7 (continued)}}


;[[MOS scale]]s
; [[WE|42et, 13-limit WE tuning]]
* Step size: 28.534{{c}}, octave size: 1198.4{{c}}
Compressing the octave of 42edo by around 1.5{{c}} results in improved primes 3, 5, 7 and 13, but worse primes 2 and 11. This approximates all harmonics up to 16 within 13.9{{c}}. Its 13-limit WE tuning and 13-limit [[TE]] tuning both do this.
 
Of the tunings discussed in this section, 13-limit WE and TE are the only ones to approximate all harmonics up to 10 within 10 cents, making them a good all-round choice.
{{Harmonics in cet|28.534|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 42et, 13-limit WE tuning}}
{{Harmonics in cet|28.534|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 42et, 13-limit WE tuning (continued)}}
 
; [[ed12|151ed12]]
* Step size: Octave size: 1196.6{{c}}
Compressing the octave of 42edo by around 3.5{{c}} results in improved primes 3, 5, 11 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 13.7{{c}}. The tuning 151ed12 does this. So do the 7-limit [[WE]] and [[TE]] tunings of 42et, whose octaves are within 0.3{{c}} of 151ed12.
{{Harmonics in equal|151|12|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 151ed12}}
{{Harmonics in equal|151|12|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 151ed12 (continued)}}
 
; [[ed6|109ed6]]
* Octave size: 1195.2{{c}}
Compressing the octave of 42edo by around 5{{c}} results in improved primes 3, 5, 11 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 14.2{{c}}. The tuning 109ed6 does this.
{{Harmonics in equal|109|6|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 109ed6}}
{{Harmonics in equal|109|6|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 109ed6 (continued)}}
 
; [[zpi|191zpi]]
* Step size: 28.444{{c}}, octave size: 1194.6{{c}}
Compressing the octave of 42edo by around 5.5{{c}} results in improved primes 3, 5, 11 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 12.4{{c}}. The tuning 191zpi does this.
{{Harmonics in cet|28.444|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 191zpi}}
{{Harmonics in cet|28.444|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 191zpi (continued)}}
 
; [[67edt]]
* Step size: 28.387{{c}}, octave size: 1192.3{{c}}
Compressing the octave of 42edo by around 7.5{{c}} results in improved primes 3, 5 and 11, but worse primes 2 and 7. This approximates all harmonics up to 16 within 12.9{{c}}. The tuning 67edt does this.
{{Harmonics in equal|67|3|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 67edt}}
{{Harmonics in equal|67|3|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 67edt (continued)}}
 
== Scales ==
{{main|List of MOS scales in 42edo}}
; [[MOS scale]]s
* Eugene/Tritikleismic[9]: '''3 8 3 3 8 3 3 8 3'''
* Eugene/Tritikleismic[9]: '''3 8 3 3 8 3 3 8 3'''
* Eugene/Tritikleismic[15]: '''3 3 2 3 3 3 3 2 3 3 3 3 2 3 3'''
* Eugene/Tritikleismic[15]: '''3 3 2 3 3 3 3 2 3 3 3 3 2 3 3'''
Line 409: Line 470:
** Yokai pentatonic: '''3 14 8 3 14'''
** Yokai pentatonic: '''3 14 8 3 14'''


==Instruments==
;Lumatone


See [[Lumatone mapping for 42edo]]
; Approximations of [[gamelan]] scales:
* 5-tone pelog: 4 5 15 3 15
* 7-tone pelog: 4 5 9 6 3 10 5
* 5-tone slendro: 8 9 8 9 8
 
== Instruments ==
=== Lumatone ===
{{main|Lumatone mapping for 42edo}}
 
=== Skip fretting ===
'''[[Skip fretting]] system 42 3 11''': One way to play [[42edo]] on a [[14edo]] guitar is to tune the strings 11\42, or approximately a [[just]] 6/5, apart. All examples on this page are for 7-string guitar.
 
; Prime intervals
1/1: string 2 open
 
2/1: string 5 fret 3
 
3/2: string 4 fret 1 and string 7 fret 4
 
5/4: string 3 fret 1
 
7/4: string 1 fret 1 and string 4 fret 4
 
11/8: string 7 fret 2
 
13/8: string 3 fret 6
 
17/16: string 1 fret 5
 
19/16: string 1 fret 7
 
23/16: string 4 open and string 7 fret 3
 
29/16: string 5 fret 1
 
31/16: string 1 fret 3 and string 4 fret 6
 
; Chords
Minor 7th: 100123X


== Music ==
== Music ==
Line 424: Line 521:
=== 21st century ===
=== 21st century ===
; [[Bryan Deister]]
; [[Bryan Deister]]
* [https://www.youtube.com/watch?v=PJw8gZyNPjg ''improv 42edo''] (2023)
* [https://www.youtube.com/watch?v=ljaSpsQP2qc ''Improvisation in 42edo''] (2023), transcribed by [[Stephen Weigel]] (2024)
* [https://www.youtube.com/watch?v=ljaSpsQP2qc ''Improvisation in 42edo''] (2023), transcribed by [[Stephen Weigel]] (2024)
; [[James Kukula]]
* ''[https://app.box.com/s/70bwqa09oq84rqehc90j5fttgqjmbxme Circulating and Traversing]'' (2024) - see the ''[https://interdependentscience.blogspot.com/2024/12/circulating-and-traversing.html composer’s notes]''


; [[Budjarn Lambeth]]
; [[Budjarn Lambeth]]
Line 436: Line 537:


[[Category:Augene]]
[[Category:Augene]]
[[Category:Todo:add rank 2 temperaments table]]
{{Todo|review|add rank 2 temperaments table}}

Latest revision as of 09:57, 30 August 2025

← 41edo 42edo 43edo →
Prime factorization 2 × 3 × 7
Step size 28.5714 ¢ 
Fifth 25\42 (714.286 ¢)
Semitones (A1:m2) 7:1 (200 ¢ : 28.57 ¢)
Dual sharp fifth 25\42 (714.286 ¢)
Dual flat fifth 24\42 (685.714 ¢) (→ 4\7)
Dual major 2nd 7\42 (200 ¢) (→ 1\6)
Consistency limit 7
Distinct consistency limit 7

42 equal divisions of the octave (abbreviated 42edo or 42ed2), also called 42-tone equal temperament (42tet) or 42 equal temperament (42et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 42 equal parts of about 28.6 ¢ each. Each step represents a frequency ratio of 21/42, or the 42nd root of 2.

Theory

42edo has a patent val fifth (the step of which is not from 7edo, this being a first for edos of the form 7n) and a third both over 12 cents sharp, using the same 400-cent interval to represent 5/4 as does 12edo, which means it tempers out 128/125. In the 7-limit, it tempers out 64/63 and 126/125, making it a tuning supporting the augene temperament.

42edo is on the optimal ET sequence of the eugene, joan, lemba, neutron, qeema, seville, sevond, skateboard, tritikleismic and vines temperaments.

42edo is a diatonic edo because its 5th falls between 4\7 = 686 ¢ and 3\5 = 720 ¢. 42edo is one of the most difficult diatonic edos to notate, because no other diatonic edo's fifth is as sharp (see 47edo for the opposite extreme).

Odd harmonics

While not an accurate tuning on the full 7-limit, 42edo does an excellent job on the 2.9.15.7.33.39 2*42 subgroup, having the same tuning on it as does 84edo. On this subgroup 42 has the same commas as 84.


Approximation of odd harmonics in 42edo
Harmonic 3 5 7 9 11 13 15 17 19 21 23
Error Absolute (¢) +12.3 +13.7 +2.6 -3.9 -8.5 -12.0 -2.6 +9.3 -11.8 -13.6 +0.3
Relative (%) +43.2 +47.9 +9.1 -13.7 -29.6 -41.8 -8.9 +32.7 -41.3 -47.7 +1.0
Steps
(reduced) 		67
(25) 		98
(14) 		118
(34) 		133
(7) 		145
(19) 		155
(29) 		164
(38) 		172
(4) 		178
(10) 		184
(16) 		190
(22)

Subsets and supersets

Since 42 factors into 2 × 3 × 7, 42edo contains subset edos 2, 3, 6, 7, 14, and 21.

Intervals

# Cents Ups and downs notation
0 0.0 P1 perfect unison D
1 28.6 ^1, m2 up unison, minor 2nd ^D, Eb
2 57.1 ^^1, ^m2 dup 1sn, upminor 2nd ^^D, ^Eb
3 85.7 ^^m2 dupminor 2nd ^^Eb
4 114.3 ^3m trupminor 2nd ^3Eb
5 143.9 v3M trudmajor 2nd v3E
6 171.4 vvM2 dudmajor 2nd vvE
7 200.0 vM2 downmajor 2nd vE
8 228.6 M2 major 2nd E
9 257.1 m3 minor 3rd F
10 285.7 ^m3 upminor 3rd ^F
11 314.3 ^^m3 dupminor 3rd ^^F
12 342.9 ^3m3 trupminor 3rd ^3F
13 371.4 v3M3 trudmajor 3rd v3F#
14 400.0 vvM3 dudmajor 3rd vvF#
15 428.6 vM3 downmajor 3rd vF#
16 457.1 M3, v4 major 3rd, down 4th F#, vG
17 485.7 P4 perfect 4th G
18 514.3 ^4 up 4th ^G
19 543.9 ^^4 dup 4th ^^G
20 571.4 ^34, ^^d5 trup 4th, dupdim 5th ^3G, ^^Ab
21 600.0 v3A4, ^3d5 trudaug 4th, trupdim 5th v3G#, ^3Ab
22 628.6 vvA4, v35 dudaug 4th, trud 5th vvG#, v3A
23 657.1 vv5 dud 5th vvA
24 685.7 v5 down 5th vA
25 714.3 P5 perfect 5th A
26 742.9 ^5, m6 up 5th, minor 6th ^A, Bb
27 771.4 ^m6 upminor 6th ^Bb
28 800.0 ^^m6 dupminor 6th ^^Bb
29 828.6 ^3m6 trupminor 6th ^3Bb
30 857.1 v3M6 trudmajor 6th v3B
31 885.7 vvM6 dudmajor 6th vvB
32 914.3 vM6 downmajor 6th vB
33 942.9 M6 major 6th B
34 971.4 m7 minor 7th C
35 1000.0 ^m7 upminor 7th ^C
36 1028.6 ^^m7 dupminor 7th ^^C
37 1057.1 ^3m7 trupminor 7th ^3C
38 1085.7 v3M7 trudmajor 7th v3C#
39 1114.3 vvM7 dudmajor 7th vvC#
40 1142.9 vM7 downmajor 7th vC#
41 1171.4 M7, v8 major 7th, down 8ve C#, vD
42 1200.0 P8 perfect 8ve D

Chords can be named using ups and downs as C upminor, D downmajor seven, etc. See Ups and downs notation #Chords and chord progressions.

Notation

Ups and downs notation

Assuming the natural notes form a chain of fifths, the major 2nd is 8 edosteps and the minor 2nd is only one. The naturals create a 5edo-like scale, with two of the notes inflected by a comma-sized edostep:

D * * * * * * * E F * * * * * * * G * * * * * * * A * * * * * * * B C * * * * * * * D

D♯ is next to E. The notation requires ups and downs with three arrows, and if chords are to be spelled correctly four or more arrows may be required in certain cases. For example, a 1/1 – 5/4 – 3/2 – 9/5 chord with a root on the edostep midway between G and A would be written either as v3G♯–v5B♯ – v3D♯ – vF♯ or as ^3A♭ – ^C – ^3E♭ – ^5G♭. This is a dud dup-seven chord, written either as v3G♯vv,^^7 or as ^3A♭vv,^^7.

In this table, dup is equivalent to quidsharp, trup is equivalent to quudsharp, trudsharp is equivalent to quup, dudsharp is equivalent to quip, etc.

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Sharp symbol                
                 
Flat symbol              
                 

Alternatively, sharps and flats with arrows borrowed from Helmholtz–Ellis notation can be used:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
Sharp symbol  
Flat symbol

Sagittal notation

Best fifth notation

This notation uses the same sagittal sequence as 35b.

Evo flavor
Sagittal notationPeriodic table of EDOs with sagittal notationapotome-fraction notation
Revo flavor
Sagittal notationPeriodic table of EDOs with sagittal notationapotome-fraction notation

Second-best fifth notation

This notation uses the same sagittal sequence as 47edo, and is a superset of the notations for edos 21, 14, and 7.

Sagittal notationPeriodic table of EDOs with sagittal notationlimma-fraction notation

Approximation to JI

The following tables show how 15-odd-limit intervals are represented in 42edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 42edo (direct approximation, even if inconsistent)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
5/3, 6/5 1.356 4.7
15/8, 16/15 2.554 8.9
7/4, 8/7 2.603 9.1
13/10, 20/13 2.929 10.3
13/11, 22/13 3.495 12.2
9/8, 16/9 3.910 13.7
13/12, 24/13 4.284 15.0
11/9, 18/11 4.551 15.9
15/14, 28/15 5.157 18.0
15/11, 22/15 5.906 20.7
11/10, 20/11 6.424 22.5
9/7, 14/9 6.513 22.8
11/6, 12/11 7.780 27.2
13/9, 18/13 8.046 28.2
11/8, 16/11 8.461 29.6
15/13, 26/15 9.402 32.9
7/6, 12/7 9.728 34.0
9/5, 10/9 10.975 38.4
11/7, 14/11 11.063 38.7
7/5, 10/7 11.084 38.8
13/8, 16/13 11.956 41.8
3/2, 4/3 12.331 43.2
5/4, 8/5 13.686 47.9
13/7, 14/13 14.013 49.0
15-odd-limit intervals in 42edo (patent val mapping)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
5/3, 6/5 1.356 4.7
7/4, 8/7 2.603 9.1
13/11, 22/13 3.495 12.2
11/8, 16/11 8.461 29.6
7/6, 12/7 9.728 34.0
9/5, 10/9 10.975 38.4
11/7, 14/11 11.063 38.7
7/5, 10/7 11.084 38.8
13/8, 16/13 11.956 41.8
3/2, 4/3 12.331 43.2
5/4, 8/5 13.686 47.9
13/7, 14/13 14.559 51.0
11/6, 12/11 20.792 72.8
9/7, 14/9 22.059 77.2
11/10, 20/11 22.147 77.5
15/14, 28/15 23.414 82.0
13/12, 24/13 24.287 85.0
9/8, 16/9 24.661 86.3
13/10, 20/13 25.643 89.7
15/8, 16/15 26.017 91.1
11/9, 18/11 33.122 115.9
15/11, 22/15 34.478 120.7
13/9, 18/13 36.618 128.2
15/13, 26/15 37.973 132.9

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3 [67 -42⟩ [⟨42 67]] −3.89 3.88 13.57
2.3.5 128/125, 5000000/4782969 [⟨42 67 98]] −4.55 3.30 11.55
2.3.5.7 64/63, 126/125, 6860/6561 [⟨42 67 98 118]] −3.65 3.26 11.42

Octave stretch or compression

42edo’s inaccurate 3rd and 5th harmonics can be greatly improved through stretching or compressing octaves. Both approaches work about equally well but in opposite directions, giving two quite different flavors of tuning to play with.

What follows is a comparison of stretched- and compressed-octave 42edo tunings.

108ed6
  • Octave size: 1206.3 ¢

Stretching the octave of 42edo by around 6 ¢ results in improved primes 3, 5 and 13, but worse primes 2, 7 and 11. This approximates all harmonics up to 16 within 13.3 ¢. The tuning 108ed6 does this. So does the tuning 97ed5 whose octave differs by only 0.1 ¢.

Approximation of harmonics in 108ed6
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) +6.3 -6.3 +12.6 -0.3 +0.0 -8.4 -9.8 -12.6 +6.0 +13.3 +6.3
Relative (%) +22.0 -22.0 +44.0 -1.0 +0.0 -29.2 -34.0 -44.0 +21.0 +46.5 +22.0
Steps
(reduced) 		42
(42) 		66
(66) 		84
(84) 		97
(97) 		108
(0) 		117
(9) 		125
(17) 		132
(24) 		139
(31) 		145
(37) 		150
(42)
Approximation of harmonics in 108ed6 (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) +11.4 -2.1 -6.6 -3.5 +6.5 -6.3 -13.8 +12.3 +14.0 -9.1 +0.1 +12.6
Relative (%) +39.5 -7.2 -23.0 -12.0 +22.5 -22.0 -47.9 +42.9 +48.9 -31.6 +0.5 +44.0
Steps
(reduced) 		155
(47) 		159
(51) 		163
(55) 		167
(59) 		171
(63) 		174
(66) 		177
(69) 		181
(73) 		184
(76) 		186
(78) 		189
(81) 		192
(84)
189zpi
  • Step size: 28.689 ¢, octave size: 1204.9 ¢

Stretching the octave of 42edo by around 5 ¢ results in improved primes 3, 5 and 13, but worse primes 2 and 11. This approximates all harmonics up to 16 within 13.9 ¢. The tuning 189zpi does this.

Approximation of harmonics in 189zpi
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) +4.9 -8.5 +9.9 -3.5 -3.5 -12.2 -13.9 +11.7 +1.5 +8.6 +1.4
Relative (%) +17.2 -29.6 +34.4 -12.1 -12.3 -42.6 -48.4 +40.9 +5.1 +29.9 +4.9
Step 42 66 84 97 108 117 125 133 139 145 150
Approximation of harmonics in 189zpi (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) +6.3 -7.3 -12.0 -8.9 +0.9 -12.0 +9.1 +6.4 +8.0 +13.5 -6.1 +6.3
Relative (%) +21.8 -25.4 -41.7 -31.2 +3.0 -41.9 +31.8 +22.3 +27.9 +47.1 -21.1 +22.1
Step 155 159 163 167 171 174 178 181 184 187 189 192
150ed12
  • Octave size: 1204.5 ¢

Stretcing the octave of 42edo by around 4.5 ¢ results in improved primes 3, 5, 11 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 13.6 ¢. The tuning 150ed12 does this.

Approximation of harmonics in 150ed12
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) +4.5 -9.1 +9.1 -4.4 -4.5 -13.3 +13.6 +10.5 +0.2 +7.2 +0.0
Relative (%) +15.9 -31.7 +31.7 -15.3 -15.9 -46.4 +47.6 +36.6 +0.6 +25.2 +0.0
Steps
(reduced) 		42
(42) 		66
(66) 		84
(84) 		97
(97) 		108
(108) 		117
(117) 		126
(126) 		133
(133) 		139
(139) 		145
(145) 		150
(0)
Approximation of harmonics in 150ed12 (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) +4.8 -8.8 -13.5 -10.5 -0.7 -13.6 +7.5 +4.7 +6.3 +11.8 -7.8 +4.5
Relative (%) +16.8 -30.5 -47.0 -36.6 -2.5 -47.6 +26.1 +16.4 +21.9 +41.1 -27.2 +15.9
Steps
(reduced) 		155
(5) 		159
(9) 		163
(13) 		167
(17) 		171
(21) 		174
(24) 		178
(28) 		181
(31) 		184
(34) 		187
(37) 		189
(39) 		192
(42)
145ed11
  • Octave size: 1202.5 ¢

Stretching the octave of 42edo by around 2.5 ¢ results in improved primes 5, 11 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 11.9 ¢. The tuning 145ed11 does this.

Approximation of harmonics in 145ed11
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) +2.5 -12.4 +4.9 -9.2 -9.9 +9.5 +7.4 +3.9 -6.8 +0.0 -7.5
Relative (%) +8.6 -43.3 +17.1 -32.2 -34.7 +33.1 +25.7 +13.4 -23.7 +0.0 -26.2
Steps
(reduced) 		42
(42) 		66
(66) 		84
(84) 		97
(97) 		108
(108) 		118
(118) 		126
(126) 		133
(133) 		139
(139) 		145
(0) 		150
(5)
Approximation of harmonics in 145ed11 (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) -2.9 +11.9 +7.0 +9.8 -9.3 +6.3 -1.4 -4.3 -2.9 +2.5 +11.4 -5.0
Relative (%) -10.2 +41.7 +24.5 +34.2 -32.4 +22.0 -4.9 -15.1 -10.1 +8.6 +39.8 -17.6
Steps
(reduced) 		155
(10) 		160
(15) 		164
(19) 		168
(23) 		171
(26) 		175
(30) 		178
(33) 		181
(36) 		184
(39) 		187
(42) 		190
(45) 		192
(47)
42edo
  • Step size: 28.571 ¢, octave size: 1200.0 ¢

Pure-octaves 42edo approximates all harmonics up to 16 within 13.7 ¢. The tuning 190zpi is almost exactly the same as pure-octaves 42edo, its octave differing by less than 0.05 ¢.

Approximation of harmonics in 42edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) +0.0 +12.3 +0.0 +13.7 +12.3 +2.6 +0.0 -3.9 +13.7 -8.5 +12.3
Relative (%) +0.0 +43.2 +0.0 +47.9 +43.2 +9.1 +0.0 -13.7 +47.9 -29.6 +43.2
Steps
(reduced) 		42
(0) 		67
(25) 		84
(0) 		98
(14) 		109
(25) 		118
(34) 		126
(0) 		133
(7) 		140
(14) 		145
(19) 		151
(25)
Approximation of harmonics in 42edo (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) -12.0 +2.6 -2.6 +0.0 +9.3 -3.9 -11.8 +13.7 -13.6 -8.5 +0.3 +12.3
Relative (%) -41.8 +9.1 -8.9 +0.0 +32.7 -13.7 -41.3 +47.9 -47.7 -29.6 +1.0 +43.2
Steps
(reduced) 		155
(29) 		160
(34) 		164
(38) 		168
(0) 		172
(4) 		175
(7) 		178
(10) 		182
(14) 		184
(16) 		187
(19) 		190
(22) 		193
(25)
118ed7
  • Step size: Octave size: 1199.1 ¢

Compressing the octave of 42edo by around 1 ¢ results in improved primes 3, 5 and 7, but worse primes 2, 11 and 13. This approximates all harmonics up to 16 within 13.2 ¢. The tuning 118ed7 does this.

Approximation of harmonics in 118ed7
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) -0.9 +10.9 -1.9 +11.5 +9.9 +0.0 -2.8 -6.8 +10.6 -11.7 +9.0
Relative (%) -3.2 +38.0 -6.5 +40.4 +34.8 +0.0 -9.7 -24.0 +37.1 -40.8 +31.5
Steps
(reduced) 		42
(42) 		67
(67) 		84
(84) 		98
(98) 		109
(109) 		118
(0) 		126
(8) 		133
(15) 		140
(22) 		145
(27) 		151
(33)
Approximation of harmonics in 118ed7 (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) +13.2 -0.9 -6.2 -3.7 +5.5 -7.8 +12.8 +9.7 +10.9 -12.6 -3.9 +8.1
Relative (%) +46.1 -3.2 -21.6 -13.0 +19.4 -27.2 +44.9 +33.9 +38.0 -44.1 -13.6 +28.3
Steps
(reduced) 		156
(38) 		160
(42) 		164
(46) 		168
(50) 		172
(54) 		175
(57) 		179
(61) 		182
(64) 		185
(67) 		187
(69) 		190
(72) 		193
(75)
42et, 13-limit WE tuning
  • Step size: 28.534 ¢, octave size: 1198.4 ¢

Compressing the octave of 42edo by around 1.5 ¢ results in improved primes 3, 5, 7 and 13, but worse primes 2 and 11. This approximates all harmonics up to 16 within 13.9 ¢. Its 13-limit WE tuning and 13-limit TE tuning both do this.

Of the tunings discussed in this section, 13-limit WE and TE are the only ones to approximate all harmonics up to 10 within 10 cents, making them a good all-round choice.

Approximation of harmonics in 42et, 13-limit WE tuning
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) -1.6 +9.8 -3.1 +10.0 +8.3 -1.8 -4.7 -8.9 +8.4 -13.9 +6.7
Relative (%) -5.5 +34.4 -11.0 +35.1 +28.9 -6.4 -16.5 -31.1 +29.6 -48.7 +23.4
Step 42 67 84 98 109 118 126 133 140 145 151
Approximation of harmonics in 42et, 13-limit WE tuning (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) +10.8 -3.4 -8.7 -6.3 +2.9 -10.5 +10.1 +6.9 +8.0 +13.1 -6.8 +5.1
Relative (%) +37.8 -11.9 -30.5 -22.0 +10.1 -36.7 +35.3 +24.1 +28.1 +45.8 -23.9 +17.9
Step 156 160 164 168 172 175 179 182 185 188 190 193
151ed12
  • Step size: Octave size: 1196.6 ¢

Compressing the octave of 42edo by around 3.5 ¢ results in improved primes 3, 5, 11 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 13.7 ¢. The tuning 151ed12 does this. So do the 7-limit WE and TE tunings of 42et, whose octaves are within 0.3 ¢ of 151ed12.

Approximation of harmonics in 151ed12
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) -3.4 +6.9 -6.9 +5.7 +3.4 -7.0 -10.3 +13.7 +2.3 +8.2 +0.0
Relative (%) -12.0 +24.1 -24.1 +19.9 +12.0 -24.7 -36.1 +48.2 +7.9 +28.7 +0.0
Steps
(reduced) 		42
(42) 		67
(67) 		84
(84) 		98
(98) 		109
(109) 		118
(118) 		126
(126) 		134
(134) 		140
(140) 		146
(146) 		151
(0)
Approximation of harmonics in 151ed12 (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) +3.9 -10.5 +12.5 -13.7 -4.7 +10.3 +2.2 -1.2 -0.2 +4.8 +13.3 -3.4
Relative (%) +13.6 -36.7 +44.0 -48.2 -16.6 +36.1 +7.6 -4.1 -0.6 +16.7 +46.6 -12.0
Steps
(reduced) 		156
(5) 		160
(9) 		165
(14) 		168
(17) 		172
(21) 		176
(25) 		179
(28) 		182
(31) 		185
(34) 		188
(37) 		191
(40) 		193
(42)
109ed6
  • Octave size: 1195.2 ¢

Compressing the octave of 42edo by around 5 ¢ results in improved primes 3, 5, 11 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 14.2 ¢. The tuning 109ed6 does this.

Approximation of harmonics in 109ed6
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) -4.8 +4.8 -9.5 +2.6 +0.0 -10.7 +14.2 +9.5 -2.2 +3.6 -4.8
Relative (%) -16.7 +16.7 -33.4 +9.1 +0.0 -37.8 +49.9 +33.4 -7.6 +12.6 -16.7
Steps
(reduced) 		42
(42) 		67
(67) 		84
(84) 		98
(98) 		109
(0) 		118
(9) 		127
(18) 		134
(25) 		140
(31) 		146
(37) 		151
(42)
Approximation of harmonics in 109ed6 (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) -1.0 +13.0 +7.4 +9.5 -10.1 +4.8 -3.5 -6.9 -6.0 -1.2 +7.3 -9.5
Relative (%) -3.6 +45.5 +25.8 +33.2 -35.6 +16.7 -12.2 -24.3 -21.1 -4.1 +25.5 -33.4
Steps
(reduced) 		156
(47) 		161
(52) 		165
(56) 		169
(60) 		172
(63) 		176
(67) 		179
(70) 		182
(73) 		185
(76) 		188
(79) 		191
(82) 		193
(84)
191zpi
  • Step size: 28.444 ¢, octave size: 1194.6 ¢

Compressing the octave of 42edo by around 5.5 ¢ results in improved primes 3, 5, 11 and 13, but worse primes 2 and 7. This approximates all harmonics up to 16 within 12.4 ¢. The tuning 191zpi does this.

Approximation of harmonics in 191zpi
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) -5.4 +3.8 -10.7 +1.2 -1.6 -12.4 +12.4 +7.6 -4.2 +1.5 -6.9
Relative (%) -18.8 +13.3 -37.6 +4.2 -5.5 -43.7 +43.6 +26.7 -14.6 +5.3 -24.3
Step 42 67 84 98 109 118 127 134 140 146 151
Approximation of harmonics in 191zpi (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) -3.3 +10.7 +5.0 +7.0 -12.6 +2.2 -6.0 -9.5 -8.6 -3.8 +4.5 -12.3
Relative (%) -11.5 +37.5 +17.5 +24.7 -44.3 +7.9 -21.2 -33.4 -30.4 -13.5 +15.9 -43.1
Step 156 161 165 169 172 176 179 182 185 188 191 193
67edt
  • Step size: 28.387 ¢, octave size: 1192.3 ¢

Compressing the octave of 42edo by around 7.5 ¢ results in improved primes 3, 5 and 11, but worse primes 2 and 7. This approximates all harmonics up to 16 within 12.9 ¢. The tuning 67edt does this.

Approximation of harmonics in 67edt
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) -7.7 +0.0 +12.9 -4.3 -7.7 +9.3 +5.2 +0.0 -12.1 -6.8 +12.9
Relative (%) -27.2 +0.0 +45.5 -15.3 -27.2 +32.7 +18.3 +0.0 -42.6 -23.8 +45.5
Steps
(reduced) 		42
(42) 		67
(0) 		85
(18) 		98
(31) 		109
(42) 		119
(52) 		127
(60) 		134
(0) 		140
(6) 		146
(12) 		152
(18)
Approximation of harmonics in 67edt (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) -12.1 +1.5 -4.3 -2.5 +6.1 -7.7 +12.2 +8.6 +9.3 +13.9 -6.3 +5.2
Relative (%) -42.6 +5.4 -15.3 -8.9 +21.4 -27.2 +43.0 +30.2 +32.7 +49.0 -22.1 +18.3
Steps
(reduced) 		156
(22) 		161
(27) 		165
(31) 		169
(35) 		173
(39) 		176
(42) 		180
(46) 		183
(49) 		186
(52) 		189
(55) 		191
(57) 		194
(60)

Scales

Main article: List of MOS scales in 42edo
MOS scales
  • Eugene/Tritikleismic[9]: 3 8 3 3 8 3 3 8 3
  • Eugene/Tritikleismic[15]: 3 3 2 3 3 3 3 2 3 3 3 3 2 3 3
  • Lemba[16]: 3 2 3 2 3 3 2 3 3 2 3 2 3 3 2 3
  • Qeema/Skateboard[15]: 2 5 2 2 2 5 2 2 2 5 2 2 2 5 2
  • Qeema/Skateboard[19]: 2 2 3 2 2 2 2 3 2 2 2 3 2 2 2 2 3 2 2
  • Seville/Sevond[14] 1st mode: 1 5 1 5 1 5 1 5 1 5 1 5 1 5
  • Seville/Sevond[14] 2nd mode: 5 1 5 1 5 1 5 1 5 1 5 1 5 1
  • Seville/Sevond[21]: 1 4 1 1 4 1 1 4 1 1 4 1 1 4 1 1 4 1 1 4


Subsets of MOS scales

(Names used are idiosyncratic.)

  • Eugene/Tritikleismic[9]
    • Groovy aeolian pentatonic: 11 6 8 3 14
    • Otonal mixolydian pentatonic: 14 3 8 11 6
    • Pseudo-equipentatonic: 11 6 8 6 11
    • Septimal melodic minor pentatonic: 8 3 14 14 3
    • Septimal Picardy pentatonic: 8 6 11 3 14
    • Undecimal lydian-aeolian pentatonic: 8 14 3 11 6
    • Yokai pentatonic: 3 14 8 3 14


Approximations of gamelan scales
  • 5-tone pelog: 4 5 15 3 15
  • 7-tone pelog: 4 5 9 6 3 10 5
  • 5-tone slendro: 8 9 8 9 8

Instruments

Lumatone

Main article: Lumatone mapping for 42edo

Skip fretting

Skip fretting system 42 3 11: One way to play 42edo on a 14edo guitar is to tune the strings 11\42, or approximately a just 6/5, apart. All examples on this page are for 7-string guitar.

Prime intervals

1/1: string 2 open

2/1: string 5 fret 3

3/2: string 4 fret 1 and string 7 fret 4

5/4: string 3 fret 1

7/4: string 1 fret 1 and string 4 fret 4

11/8: string 7 fret 2

13/8: string 3 fret 6

17/16: string 1 fret 5

19/16: string 1 fret 7

23/16: string 4 open and string 7 fret 3

29/16: string 5 fret 1

31/16: string 1 fret 3 and string 4 fret 6

Chords

Minor 7th: 100123X

Music

Modern renderings

Johann Sebastian Bach
Bing Crosby

21st century

Bryan Deister
James Kukula
Budjarn Lambeth
Herman Miller
Mundoworld
Retrieved from "https://en.xen.wiki/index.php?title=42edo&oldid=208864"