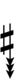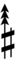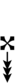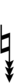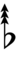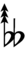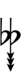54edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older editNewer edit →
VisualWikitext
CompactStar (talk | contribs)
5,020 edits
No edit summary
→Instruments: Insert music section after this, starting with Bryan Deister's ''microtonal improvisation in 54edo'' (2025)
(33 intermediate revisions by 8 users not shown)
Line 1: Line 1:
Ex, Fbbbbbb{{Infobox ET}}
{{Infobox ET}}
{{EDO intro|54}}
{{ED intro}}


== Theory ==
== Theory ==
54edo is suitable for usage with [[dual-fifth tuning]] systems, or alternately, no-fifth tuning systems. 54edo has an ultrahard diatonic scale using the sharp fifth of [[27edo]] and an ultrasoft diatonic using the flat fifth. The soft diatonic scale is so soft, with L/s = 8/7, that it stops sounding like [[meantone]] or even [[flattone]], but just sounds like a [[circulating temperament]] of [[7edo]].
54edo is suitable for usage as a [[dual-fifth tuning]] system, or alternatively, a [[No-threes subgroup temperaments|no-fifth]] tuning system. Using the sharp fifth, it can be viewed as two [[ring number|rings]] of [[27edo]], which adds better approximations of the [[11/1|11th]] and [[15/1|15th harmonics]]. Using the flat fifth, it generates an ultrasoft [[diatonic scale]]. This scale is so [[soft]], with {{nowrap|L/s {{=}} 8/7}}, that it stops sounding like [[meantone]] or even [[flattone]], but just sounds like a [[circulating temperament]] of [[7edo]].


It's a rare temperament which adds better approximations of the 11th and 15th harmonics from [[27edo]], which it doubles. 54edo contains an alternate (flat) mapping of the fifth and an "extreme bayati" 6 6 10 10 2 10 10 diatonic scale.
The [[patent val]] of this edo takes the same fifth as [[27edo]], but the [[mapping]] for harmonic 5 is different. It tempers out [[2048/2025]] in the 5-limit, making it a [[diaschismic]] system. It is the highest edo in which the best mappings of the major 3rd ([[5/4]]) and harmonic 7th ([[7/4]]), 17\54 and 44\54, are exactly 600{{c}} apart, making them suitable for harmonies using tritone substitutions. In other words, this is the last edo tempering out [[50/49]]. This means it extends quite simply to the 7- and 11-limit using the [[pajarous]] mapping and to the 13-limit using the 54f val, falling neatly between the 7- and 13-limit [[Target tuning #Minimax tuning|minimax tunings]].  


It is the highest [[EDO]] in which the best mappings of the major 3rd ([[5/4]]) and harmonic 7th ([[7/4]]), 17\54 and 44\54, are exactly 600 cents apart, making them suitable for harmonies using tritone substitutions. In other words, this is the last EDO tempering out [[50/49]]. The 54cd val makes for an excellent tuning of 7-limit [[Augmented_family#Hexe|hexe temperament]], while the bdf val does higher limit [[Magic family #Muggles|muggles]] about as well as it can be tuned.
The 54cd val makes for an excellent tuning of 7-limit [[hexe]] temperament, while the 54bdf val does higher limit [[muggles]] about as well as it can be tuned. However, even these best temperament interpretations of 54edo are quite high in [[badness]] compared to its immediate neighbours [[53edo|53-]] and [[55edo]], both of which are [[Historical temperaments|historically significant]] for different reasons, leaving it mostly unexplored so far.


Using the patent val, 54edo tempers out [[2048/2025]] in the 5-limit.
=== Odd harmonics ===
{{Harmonics in equal|54}}


The immediate close presence of [[53edo]] obscures 54edo and puts this temperament out of popular usage.
=== Octave stretch ===
===Odd harmonics===
54edo’s approximations of 3/1, 5/1, 7/1, 11/1, 13/1, 17/1, 19/1 and 23/1 are all improved by [[Gallery of arithmetic pitch sequences#APS of mérides|APS4/5méride]], a [[Octave stretch|stretched-octave]] version of 54edo. The trade-off is a slightly worse 2/1.
{{harmonics in equal|54}}
==Intervals==
Using the sharp fifth as a generator, 54edo require a large amount of ups and downs to notate, and using the flat fifth as a generator, 54edo requires a large amount of sharps and flats to notate. Because the flat fifth generates a diatonic scale with a chroma of 1 step, ups and downs are not needed in notation if the flat fifth is used.


{| class="wikitable mw-collapsible mw-collapsed"
If one prefers a ''[[Octave shrinking|compressed-octave]]'' tuning instead, [[86edt]], [[126ed5]] and [[152ed7]] are possible choices. They improve upon 54edo’s  3/1, 5/1, 7/1 and 17/1, at the cost of its 2/1, 11/1 and 13/1.
|+Table of intervals
 
!Degree
[[ed255/128#54ed255/128|54ed255/128]] is another compressed octave option. It improves upon 54edo’s 3/1, 5/1, 11/1, 13/1, 17/1 and 19/1, at slight cost to the 2/1 and 7/1. Its 2/1 is the least accurate of all the tunings mentioned in this section, though still accurate enough that it has low [[harmonic entropy]].
!Cents
 
!Approximate Ratios
There are also some nearby [[Zeta peak index]] (ZPI) tunings which can be used to improve 54edo’s approximation of JI: 262zpi, 263zpi, 264zpi and 265zpi. The main Zeta peak index page details all four tunings.
![[Ups and downs notation]] using flat fifth
 
=== Subsets and supersets ===
Since 54 factors into {{factorization|54}}, 54edo has subset edos {{EDOs| 2, 3, 6, 9, 18, and 27 }}.
 
== Intervals ==
Using the sharp fifth as a [[generator]], 54edo requires up to quadruple ups and downs to notate. But using the flat fifth as a generator, it requires up to septuple sharps and flats. Because the flat fifth generates a diatonic scale with a [[chroma]] of 1 step, ups and downs are not needed in notation if the flat fifth is used.
 
{| class="wikitable"
|+ style="font-size: 105%;" | Table of intervals in 54edo
|-
! rowspan="2" | Degree
! rowspan="2" | Cents
! colspan="2" | [[Ups and downs notation]]
|-
! Flat fifth (31\54)
! Sharp fifth (16\27)
|-
| 0
| 0.000
| {{UDnote|fifth=31|step=0}}
| {{UDnote|step=0}}
|-
| 1
| 22.222
| {{UDnote|fifth=31|step=1}}
| {{UDnote|step=1}}
|-
| 2
| 44.444
| {{UDnote|fifth=31|step=2}}
| {{UDnote|step=2}}
|-
| 3
| 66.667
| {{UDnote|fifth=31|step=3}}
| {{UDnote|step=3}}
|-
| 4
| 88.889
| {{UDnote|fifth=31|step=4}}
| {{UDnote|step=4}}
|-
| 5
| 111.111
| {{UDnote|fifth=31|step=5}}
| {{UDnote|step=5}}
|-
| 6
| 133.333
| {{UDnote|fifth=31|step=6}}
| {{UDnote|step=6}}
|-
| 7
| 155.556
| {{UDnote|fifth=31|step=7}}
| {{UDnote|step=7}}
|-
| 8
| 177.778
| {{UDnote|fifth=31|step=8}}
| {{UDnote|step=8}}
|-
| 9
| 200.000
| {{UDnote|fifth=31|step=9}}
| {{UDnote|step=9}}
|-
| 10
| 222.222
| {{UDnote|fifth=31|step=10}}
| {{UDnote|step=10}}
|-
| 11
| 244.444
| {{UDnote|fifth=31|step=11}}
| {{UDnote|step=11}}
|-
| 12
| 266.667
| {{UDnote|fifth=31|step=12}}
| {{UDnote|step=12}}
|-
| 13
| 288.889
| {{UDnote|fifth=31|step=13}}
| {{UDnote|step=13}}
|-
| 14
| 311.111
| {{UDnote|fifth=31|step=14}}
| {{UDnote|step=14}}
|-
|-
|0
| 15
|0.000
| 333.333
|[[1/1]]
| {{UDnote|fifth=31|step=15}}
|C
| {{UDnote|step=15}}
|-
|-
|1
| 16
|22.222
| 355.556
|[[81/80]], [[64/63]]
| {{UDnote|fifth=31|step=16}}
|C#, Dbbbbbbb
| {{UDnote|step=16}}
|-
|-
|2
| 17
|44.444
| 377.778
|[[128/125]], [[36/35]]
| {{UDnote|fifth=31|step=17}}
|Cx, Dbbbbbb
| {{UDnote|step=17}}
|-
|-
|3
| 18
|66.666
| 400.000
|[[28/27]], [[25/24]]
| {{UDnote|fifth=31|step=18}}
|Cx#, Dbbbbb
| {{UDnote|step=18}}
|-
|4
|88.888
|[[19/18]], [[20/19]]
|Cxx, Dbbbb
|-
|-
|5
| 19
|111.111
| 422.222
|[[16/15]]
| {{UDnote|fifth=31|step=19}}
|Cxx#, Dbbb
| {{UDnote|step=19}}
|-
|-
|6
| 20
|133.333
| 444.444
|[[13/12]]
| {{UDnote|fifth=31|step=20}}
|Cxxx, Dbb
| {{UDnote|step=20}}
|-
|-
|7
| 21
|155.555
| 466.667
|[[12/11]], [[11/10]]
| {{UDnote|fifth=31|step=21}}
|Cxxx#, Db
| {{UDnote|step=21}}
|-
|-
|8
| 22
|Minor whole tone
| 488.889
|177.777
| {{UDnote|fifth=31|step=22}}
|[[10/9]]
| {{UDnote|step=22}}
|D
|-
|-
|9
| 23
|Symmetric whole tone
| 511.111
|200.000
| {{UDnote|fifth=31|step=23}}
|[[9/8]]
| {{UDnote|step=23}}
|D#, Ebbbbbbb
|-
|-
|10
| 24
|222.222
| 533.333
|[[8/7]], [[17/15]]
| {{UDnote|fifth=31|step=24}}
|Dx, Ebbbbbb
| {{UDnote|step=24}}
|-
|-
|11
| 25
|244.444
| 555.556
|[[15/13]], [[23/20]]
| {{UDnote|fifth=31|step=25}}
|Dx#, Ebbbbb
| {{UDnote|step=25}}
|-
|-
|12
| 26
|Septimal submajor third
| 577.778
|266.666
| {{UDnote|fifth=31|step=26}}
|[[7/6]]
| {{UDnote|step=26}}
|Dxx, Ebbbb
|-
|-
|13
| 27
|Gothic minor third
| 600.000
|288.888
| {{UDnote|fifth=31|step=27}}
|[[13/11]], [[20/17]]
| {{UDnote|step=27}}
|Dxx#, Ebbb
|-
|-
|14
| 28
|Classical minor third
| 622.222
|311.111
| {{UDnote|fifth=31|step=28}}
|[[6/5]], [[19/16]]
| {{UDnote|step=28}}
|Dxxx, Ebb
|-
|-
|15
| 29
|
| 644.444
|333.333
| {{UDnote|fifth=31|step=29}}
|[[17/14]]
| {{UDnote|step=29}}
|Dxxx#, Eb
|-
|-
|16
| 30
|
| 666.667
|355.555
| {{UDnote|fifth=31|step=30}}
|[[11/9]], [[27/22]], [[16/13]]
| {{UDnote|step=30}}
|E
|-
|-
|17
| 31
|377.777
| 688.889
|[[5/4]]
| {{UDnote|fifth=31|step=31}}
|E#, Fbbbbbb
| {{UDnote|step=31}}
|-
|-
|18
| 32
|400.000
| 711.111
|[[5/4]], [[29/23]], [[14/11]]
| {{UDnote|fifth=31|step=32}}
|Ex, Fbbbbb
| {{UDnote|step=32}}
|-
|-
|19
| 33
|422.222
| 733.333
|[[14/11], [[9/7]]
| {{UDnote|fifth=31|step=33}}
|Ex#, Fbbbb
| {{UDnote|step=33}}
|-
|-
|20
| 34
|444.444
| 755.556
|[[9/7]], [[35/27]], [[13/10]]
| {{UDnote|fifth=31|step=34}}
|Exx, Fbbb
| {{UDnote|step=34}}
|-
|-
|21
| 35
|466.666
| 777.778
|[[21/16]]
| {{UDnote|fifth=31|step=35}}
|Exx#, Fbb
| {{UDnote|step=35}}
|-
|-
|22
| 36
|488.888
| 800.000
|[[4/3]]
| {{UDnote|fifth=31|step=36}}
|Exxx, Fb
| {{UDnote|step=36}}
|-
|-
|23
| 37
|511.111
| 822.222
|[[4/3]]
| {{UDnote|fifth=31|step=37}}
|F
| {{UDnote|step=37}}
|-
|-
|23
| 38
|533.333
| 844.444
|[[4/3]]
| {{UDnote|fifth=31|step=38}}
|F#, Gbbbbbbb
| {{UDnote|step=38}}
|-
|-
|24
| 39
|555.555
| 866.667
|[[4/3]]
| {{UDnote|fifth=31|step=39}}
|Fx, Gbbbbbb
| {{UDnote|step=39}}
|-
|-
|25
| 40
|577.777
| 888.889
|[[4/3]]
| {{UDnote|fifth=31|step=40}}
|Fxx, Gbbbbb
| {{UDnote|step=40}}
|-
| 41
| 911.111
| {{UDnote|fifth=31|step=41}}
| {{UDnote|step=41}}
|-
| 42
| 933.333
| {{UDnote|fifth=31|step=42}}
| {{UDnote|step=42}}
|-
| 43
| 955.556
| {{UDnote|fifth=31|step=43}}
| {{UDnote|step=43}}
|-
| 44
| 977.778
| {{UDnote|fifth=31|step=44}}
| {{UDnote|step=44}}
|-
| 45
| 1000.000
| {{UDnote|fifth=31|step=45}}
| {{UDnote|step=45}}
|-
| 46
| 1022.222
| {{UDnote|fifth=31|step=46}}
| {{UDnote|step=46}}
|-
| 47
| 1044.444
| {{UDnote|fifth=31|step=47}}
| {{UDnote|step=47}}
|-
| 48
| 1066.667
| {{UDnote|fifth=31|step=48}}
| {{UDnote|step=48}}
|-
| 49
| 1088.889
| {{UDnote|fifth=31|step=49}}
| {{UDnote|step=49}}
|-
| 50
| 1111.111
| {{UDnote|fifth=31|step=50}}
| {{UDnote|step=50}}
|-
| 51
| 1133.333
| {{UDnote|fifth=31|step=51}}
| {{UDnote|step=51}}
|-
| 52
| 1155.556
| {{UDnote|fifth=31|step=52}}
| {{UDnote|step=52}}
|-
| 53
| 1177.778
| {{UDnote|fifth=31|step=53}}
| {{UDnote|step=53}}
|-
| 54
| 1200.000
| {{UDnote|fifth=31|step=54}}
| {{UDnote|step=54}}
|}
|}


[[Category:Equal divisions of the octave|##]] <!-- 2-digit number -->
== Notation ==
=== Ups and downs notation ===
Using [[Helmholtz–Ellis]] accidentals, 54edo can also be notated using [[ups and downs notation]]:
{{Sharpness-sharp8}}
Here, a sharp raises by eight steps, and a flat lowers by eight steps, so single, double, and triple arrows along with Stein–Zimmerman [[24edo#Notation|quarter-tone]] accidentals can be used to fill in the gap.
 
=== Sagittal notation ===
This notation uses the same sagittal sequence as [[61edo#Sagittal notation|61-EDO]], and is a superset of the notation for [[27edo#Sagittal notation|27-EDO]].
 
==== Evo flavor ====
<imagemap>
File:54-EDO_Evo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 650 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 140 106 [[513/512]]
rect 140 80 240 106 [[81/80]]
rect 240 80 360 106 [[33/32]]
rect 360 80 480 106 [[27/26]]
default [[File:54-EDO_Evo_Sagittal.svg]]
</imagemap>
 
==== Revo flavor ====
<imagemap>
File:54-EDO_Revo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 650 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 140 106 [[513/512]]
rect 140 80 240 106 [[81/80]]
rect 240 80 360 106 [[33/32]]
rect 360 80 480 106 [[27/26]]
default [[File:54-EDO_Revo_Sagittal.svg]]
</imagemap>
 
==== Evo-SZ flavor ====
<imagemap>
File:54-EDO_Evo-SZ_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 642 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 140 106 [[513/512]]
rect 140 80 240 106 [[81/80]]
rect 240 80 360 106 [[33/32]]
rect 360 80 480 106 [[27/26]]
default [[File:54-EDO_Evo-SZ_Sagittal.svg]]
</imagemap>
 
In the diagrams above, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's [[Sagittal notation#Primary comma|primary comma]] (the comma it ''exactly'' represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it ''approximately'' represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this EDO.
 
== Scales ==
* Approximations of [[gamelan]] scales:
** 5-tone pelog: 5 7 19 4 19
** 7-tone pelog: 5 7 11 8 4 13 6
** 5-tone slendro: 11 11 10 11 11
 
== Instruments ==
; Lumatone
 
See [[Lumatone mapping for 54edo]]
 
[[Category:Todo:add rank 2 temperaments table]]
 
== Music ==
 
; [[Bryan Deister]]
* [https://www.youtube.com/shorts/Bi5-YQUQHek ''microtonal improvisation in 54edo''] (2025)

Revision as of 08:28, 8 May 2025

← 53edo 54edo 55edo →
Prime factorization 2 × 33
Step size 22.2222 ¢ 
Fifth 32\54 (711.111 ¢) (→ 16\27)
Semitones (A1:m2) 8:2 (177.8 ¢ : 44.44 ¢)
Dual sharp fifth 32\54 (711.111 ¢) (→ 16\27)
Dual flat fifth 31\54 (688.889 ¢)
Dual major 2nd 9\54 (200 ¢) (→ 1\6)
Consistency limit 3
Distinct consistency limit 3

54 equal divisions of the octave (abbreviated 54edo or 54ed2), also called 54-tone equal temperament (54tet) or 54 equal temperament (54et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 54 equal parts of about 22.2 ¢ each. Each step represents a frequency ratio of 21/54, or the 54th root of 2.

Theory

54edo is suitable for usage as a dual-fifth tuning system, or alternatively, a no-fifth tuning system. Using the sharp fifth, it can be viewed as two rings of 27edo, which adds better approximations of the 11th and 15th harmonics. Using the flat fifth, it generates an ultrasoft diatonic scale. This scale is so soft, with L/s = 8/7, that it stops sounding like meantone or even flattone, but just sounds like a circulating temperament of 7edo.

The patent val of this edo takes the same fifth as 27edo, but the mapping for harmonic 5 is different. It tempers out 2048/2025 in the 5-limit, making it a diaschismic system. It is the highest edo in which the best mappings of the major 3rd (5/4) and harmonic 7th (7/4), 17\54 and 44\54, are exactly 600 ¢ apart, making them suitable for harmonies using tritone substitutions. In other words, this is the last edo tempering out 50/49. This means it extends quite simply to the 7- and 11-limit using the pajarous mapping and to the 13-limit using the 54f val, falling neatly between the 7- and 13-limit minimax tunings.

The 54cd val makes for an excellent tuning of 7-limit hexe temperament, while the 54bdf val does higher limit muggles about as well as it can be tuned. However, even these best temperament interpretations of 54edo are quite high in badness compared to its immediate neighbours 53- and 55edo, both of which are historically significant for different reasons, leaving it mostly unexplored so far.

Odd harmonics

Approximation of odd harmonics in 54edo
Harmonic 3 5 7 9 11 13 15 17 19 21 23
Error Absolute (¢) +9.16 -8.54 +8.95 -3.91 +4.24 +3.92 +0.62 +6.16 -8.62 -4.11 -6.05
Relative (%) +41.2 -38.4 +40.3 -17.6 +19.1 +17.6 +2.8 +27.7 -38.8 -18.5 -27.2
Steps
(reduced) 		86
(32) 		125
(17) 		152
(44) 		171
(9) 		187
(25) 		200
(38) 		211
(49) 		221
(5) 		229
(13) 		237
(21) 		244
(28)

Octave stretch

54edo’s approximations of 3/1, 5/1, 7/1, 11/1, 13/1, 17/1, 19/1 and 23/1 are all improved by APS4/5méride, a stretched-octave version of 54edo. The trade-off is a slightly worse 2/1.

If one prefers a compressed-octave tuning instead, 86edt, 126ed5 and 152ed7 are possible choices. They improve upon 54edo’s 3/1, 5/1, 7/1 and 17/1, at the cost of its 2/1, 11/1 and 13/1.

54ed255/128 is another compressed octave option. It improves upon 54edo’s 3/1, 5/1, 11/1, 13/1, 17/1 and 19/1, at slight cost to the 2/1 and 7/1. Its 2/1 is the least accurate of all the tunings mentioned in this section, though still accurate enough that it has low harmonic entropy.

There are also some nearby Zeta peak index (ZPI) tunings which can be used to improve 54edo’s approximation of JI: 262zpi, 263zpi, 264zpi and 265zpi. The main Zeta peak index page details all four tunings.

Subsets and supersets

Since 54 factors into 2 × 33, 54edo has subset edos 2, 3, 6, 9, 18, and 27.

Intervals

Using the sharp fifth as a generator, 54edo requires up to quadruple ups and downs to notate. But using the flat fifth as a generator, it requires up to septuple sharps and flats. Because the flat fifth generates a diatonic scale with a chroma of 1 step, ups and downs are not needed in notation if the flat fifth is used.

Table of intervals in 54edo
Degree Cents Ups and downs notation
Flat fifth (31\54) Sharp fifth (16\27)
0 0.000 D D
1 22.222 D♯, E♭♭♭♭♭♭♭ ^D, vE♭
2 44.444 D𝄪, E♭♭♭♭♭♭ ^^D, E♭
3 66.667 D♯𝄪, E♭♭♭♭♭ ^3D, ^E♭
4 88.889 D𝄪𝄪, E♭♭♭♭ ^4D, ^^E♭
5 111.111 D♯𝄪𝄪, E♭♭♭ v3D♯, ^3E♭
6 133.333 D𝄪𝄪𝄪, E♭♭ vvD♯, v4E
7 155.556 D♯𝄪𝄪𝄪, E♭ vD♯, v3E
8 177.778 E D♯, vvE
9 200.000 E♯, F♭♭♭♭♭♭ ^D♯, vE
10 222.222 E𝄪, F♭♭♭♭♭ E
11 244.444 E♯𝄪, F♭♭♭♭ ^E, vF
12 266.667 E𝄪𝄪, F♭♭♭ F
13 288.889 E♯𝄪𝄪, F♭♭ ^F, vG♭
14 311.111 E𝄪𝄪𝄪, F♭ ^^F, G♭
15 333.333 F ^3F, ^G♭
16 355.556 F♯, G♭♭♭♭♭♭♭ ^4F, ^^G♭
17 377.778 F𝄪, G♭♭♭♭♭♭ v3F♯, ^3G♭
18 400.000 F♯𝄪, G♭♭♭♭♭ vvF♯, v4G
19 422.222 F𝄪𝄪, G♭♭♭♭ vF♯, v3G
20 444.444 F♯𝄪𝄪, G♭♭♭ F♯, vvG
21 466.667 F𝄪𝄪𝄪, G♭♭ ^F♯, vG
22 488.889 F♯𝄪𝄪𝄪, G♭ G
23 511.111 G ^G, vA♭
24 533.333 G♯, A♭♭♭♭♭♭♭ ^^G, A♭
25 555.556 G𝄪, A♭♭♭♭♭♭ ^3G, ^A♭
26 577.778 G♯𝄪, A♭♭♭♭♭ ^4G, ^^A♭
27 600.000 G𝄪𝄪, A♭♭♭♭ v3G♯, ^3A♭
28 622.222 G♯𝄪𝄪, A♭♭♭ vvG♯, v4A
29 644.444 G𝄪𝄪𝄪, A♭♭ vG♯, v3A
30 666.667 G♯𝄪𝄪𝄪, A♭ G♯, vvA
31 688.889 A ^G♯, vA
32 711.111 A♯, B♭♭♭♭♭♭♭ A
33 733.333 A𝄪, B♭♭♭♭♭♭ ^A, vB♭
34 755.556 A♯𝄪, B♭♭♭♭♭ ^^A, B♭
35 777.778 A𝄪𝄪, B♭♭♭♭ ^3A, ^B♭
36 800.000 A♯𝄪𝄪, B♭♭♭ ^4A, ^^B♭
37 822.222 A𝄪𝄪𝄪, B♭♭ v3A♯, ^3B♭
38 844.444 A♯𝄪𝄪𝄪, B♭ vvA♯, v4B
39 866.667 B vA♯, v3B
40 888.889 B♯, C♭♭♭♭♭♭ A♯, vvB
41 911.111 B𝄪, C♭♭♭♭♭ ^A♯, vB
42 933.333 B♯𝄪, C♭♭♭♭ B
43 955.556 B𝄪𝄪, C♭♭♭ ^B, vC
44 977.778 B♯𝄪𝄪, C♭♭ C
45 1000.000 B𝄪𝄪𝄪, C♭ ^C, vD♭
46 1022.222 C ^^C, D♭
47 1044.444 C♯, D♭♭♭♭♭♭♭ ^3C, ^D♭
48 1066.667 C𝄪, D♭♭♭♭♭♭ ^4C, ^^D♭
49 1088.889 C♯𝄪, D♭♭♭♭♭ v3C♯, ^3D♭
50 1111.111 C𝄪𝄪, D♭♭♭♭ vvC♯, v4D
51 1133.333 C♯𝄪𝄪, D♭♭♭ vC♯, v3D
52 1155.556 C𝄪𝄪𝄪, D♭♭ C♯, vvD
53 1177.778 C♯𝄪𝄪𝄪, D♭ ^C♯, vD
54 1200.000 D D

Notation

Ups and downs notation

Using Helmholtz–Ellis accidentals, 54edo can also be notated using ups and downs notation:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
Sharp symbol  
Flat symbol

Here, a sharp raises by eight steps, and a flat lowers by eight steps, so single, double, and triple arrows along with Stein–Zimmerman quarter-tone accidentals can be used to fill in the gap.

Sagittal notation

This notation uses the same sagittal sequence as 61-EDO, and is a superset of the notation for 27-EDO.

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation513/51281/8033/3227/26

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation513/51281/8033/3227/26

Evo-SZ flavor

Sagittal notationPeriodic table of EDOs with sagittal notation513/51281/8033/3227/26

In the diagrams above, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's primary comma (the comma it exactly represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it approximately represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this EDO.

Scales

  • Approximations of gamelan scales:
    • 5-tone pelog: 5 7 19 4 19
    • 7-tone pelog: 5 7 11 8 4 13 6
    • 5-tone slendro: 11 11 10 11 11

Instruments

Lumatone

See Lumatone mapping for 54edo

Music

Bryan Deister
Retrieved from "https://en.xen.wiki/index.php?title=54edo&oldid=195752"