Temperament merging
| This is a beginner page. It is written to allow new readers to learn about the basics of the topic easily. The corresponding expert page for this topic is Meet and join. |
Temperament merging is a way to find new regular temperaments by merging others. There are two ways to merge temperaments: joining (or map-merge), which works by merging the temperaments' mappings, and comma-merge, which works by merging the temperaments' comma bases.
These are multiple ways in which a temperament can be defined in terms of the properties of another temperament.
Joining two temperaments a and b (notated a & b) results in a higher-rank temperament which tempers out only the commas that both a and b temper out. Usually, this is done with two ETs (vals, usually written in wart notation) to receive a rank-2 temperament (sometimes called cross-breeding), and indeed, all possible rank-2 temperaments can be written as a combination of two ETs. The resulting rank-2 essentially captures the similarities between the two ETs: 15 & 22 is porcupine, because both ETs have an 11/10 that doubles to 6/5 and triples to 4/3. Similarly, 19 & 26 is flattone, because in the diatonic scale of both edos, the major third is 5/4 and the diminished seventh is 7/4. Higher-rank temperaments can also be joined; garibaldi & rodan is hemifamity, because both garibaldi and rodan conflate 81/80 and 64/63 into a single comma-sized interval.
Comma-merging two temperaments a and b (notated a | b) results in a lower-rank temperament which tempers out all of the commas that either a or b temper out. This can be done with two rank-2 temperaments to find the equal temperament which supports them both. For example, meantone | augmented is 12-ET, since 12-ET both has 5/4 as its diatonic major third and has that 5/4 equal to 1\3 of the octave.
More than two temperaments may be merged at once. For example, joining three ETs results in a rank-3 temperament (e.g. 22 & 34d & 37 is ares).
Note that while a given temperament merging expression unambiguously refers to a single temperament, a given temperament can be expressed by many possible different temperament merging expressions.
With mappings
To perform the join with mappings, we vertically concatenate the matrices. In this form, the mapping does represent the temperament (and is the form used in diatonic, chromatic, enharmonic, and subchromatic theory), but to get a more conventional mapping, we can then canonicalize it.
Similarly, to perform the join with comma bases, we horizontally concatenate them, and then canonicalize the result.
[math]\displaystyle{ \hspace{1cm} \begin{array} {ccc} \left[ \begin{matrix} 12 & 19 & 28 \\ \end{matrix} \right] \\ \text{map-merge} \\ \left[ \begin{matrix} 19 & 30 & 44 \\ \end{matrix} \right] \\ ↓ \\ \left[ \begin{matrix} 12 & 19 & 28 \\ 19 & 30 & 44 \\ \end{matrix} \right] \\ \text{which canonicalizes to} \\ \left[ \begin{matrix} 1 & 0 & -4 \\ 0 & 1 & 4 \\ \end{matrix} \right] \\ \end{array} \hspace{1cm} \hspace{1cm} \left[ \begin{matrix} -4 \\ 4 \\ -1 \\ \end{matrix} \right] \text{comma-merge} \left[ \begin{matrix} 7 \\ 0 \\ -3 \\ \end{matrix} \right] → \left[ \begin{matrix} -4 & 7 \\ 4 & 0 \\ -1 & -3 \\ \end{matrix} \right] \text{which canonicalizes to} \left[ \begin{matrix} -19 & -15 \\ 12 & 8 \\ 0 & 1 \\ \end{matrix} \right] }[/math]
With multivals
Joining is equivalent to the wedge product, and can be calculated in that manner. Wedging two vals results in the same temperament (in wedgie form) as joining them does.
Canonicalization
The canonicalization step is important for eliminating any redundancies that may have been introduced by merging related temperaments, such as rank-deficiencies or enfactoring.
Rank-deficiencies
Sometimes when temperaments are merged, rank-deficiencies may occur. For example, comma-merging septimal meantone and miracle temperaments:
[math]\displaystyle{
\left[ \begin{array} {r|r}
4 & 13 \\
-4 & -10 \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
|
\left[ \begin{array} {r|r}
-25 & -20 \\
7 & 5 \\
6 & 4 \\
0 & 1 \\
\end{array} \right]
→
\left[ \begin{array} {r|r|r|r}
4 & 13 & -25 & -20 \\
-4 & -10 & 7 & 5 \\
1 & 0 & 6 & 4 \\
0 & 1 & 0 & 1 \\
\end{array} \right]
\text{which in canonical form* is}
\left[ \begin{array} {r|r|r|r}
\style{background-color:#F2B2B4;padding:5px}{0} & -49 & -45 & -36 \\
\style{background-color:#F2B2B4;padding:5px}{0} & 31 & 27 & 21 \\
\style{background-color:#F2B2B4;padding:5px}{0} & 0 & 1 & 0 \\
\style{background-color:#F2B2B4;padding:5px}{0} & 0 & 0 & 1 \\
\end{array} \right]
}[/math]
We haven't completely canonicalized yet; we didn't remove the all-zero column (highlighted in red) that was created by the Hermite normal form step. The existence of any all-zero columns like this tells us that our matrix was column-rank-deficient, or in layperson's terms, that it contained redundant commas. In other words, these two temperaments make some of the same commas vanish, and so when we merged them—even though the input temperaments required 2 vectors each to represent—their merged result doesn't require all 4 vectors; it can be completely represented using only 3 vectors. So once we fully canonicalize, any all-zero column(s) are removed, and we end up with:
[math]\displaystyle{
\left[ \begin{array} {r|r|r}
-49 & -45 & -36 \\
31 & 27 & 21 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{array} \right]
}[/math]
Enfactoring
Sometimes when temperaments are merged, enfactoring may occur. For example:
[math]\displaystyle{
\begin{array} {ccc}
\left[ \begin{array} {rrr}
5 & 8 & 12 \\
\end{array} \right] \\
\& \\
\left[ \begin{array} {rrr}
19 & 30 & 44 \\
\end{array} \right] \\
↓ \\
\left[ \begin{array} {rrr}
5 & 8 & 12 \\
19 & 30 & 44 \\
\end{array} \right] \\
\end{array}
}[/math]
The greatest factor of this matrix is 2, because we can produce the row ⟨24 38 56] as a coprime linear combination of its rows (that's ⟨5 8 12] + ⟨19 30 44]), and the entries of this row have a GCD of 2, so in other words this matrix is 2-enfactored. If we merely put it into Hermite normal form, we receive:
[math]\displaystyle{
\left[ \begin{array} {rrr}
1 & 0 & -4 \\
0 & 2 & 8 \\
\end{array} \right]
}[/math]
which is a 2-enfactored meantone mapping, and it reveals the greatest factor as the GCD of the second row. But if we fully canonicalize it (defactor, and put into normal form), then we get:
[math]\displaystyle{
\left[ \begin{array} {rrr}
1 & 0 & -4 \\
0 & 1 & 4 \\
\end{array} \right]
}[/math]
which is simply the canonical mapping for meantone temperament.
Non-canonicalizing definition
By some definitions of the & operator, the defactoring part of canonicalization is not include—for example on Graham Breed's temperament finding tool. This allows for things like 5 & 19 to represent 2-enfactored meantone, rather than meantone itself. Instead of a full canonicalization, then, this definition merely puts the result into Hermite normal form and removes any all-zero rows or columns resulting from rank-deficiencies.
Parallel intersections
Every temperament mapping has a dual comma basis, and every comma basis has a dual mapping. Because of this duality, a special parallelism exists.
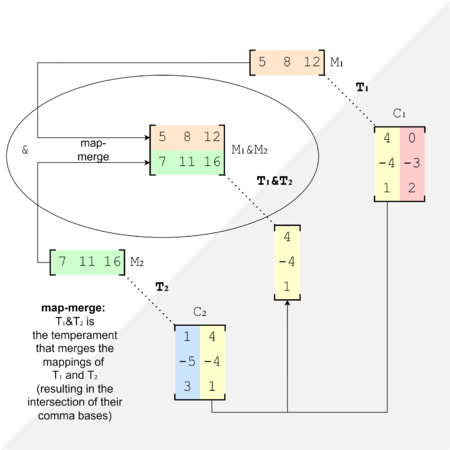
If we perform a map-merge, then look at the resultant mapping's comma basis, we'll find that it is the intersection of the input temperaments' comma bases. In other words, and like stated earlier, it includes only the commas that were in both of their comma bases.
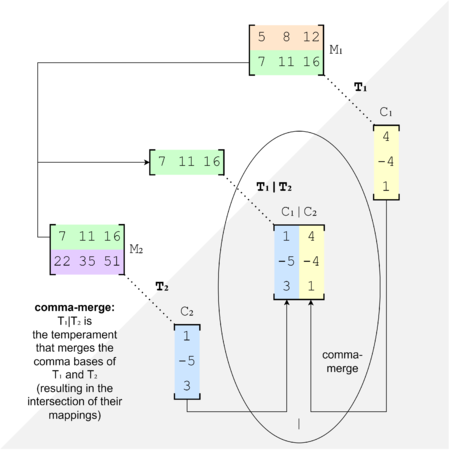
Similarly, if we perform a comma-merge, then look at the resultant comma basis's mapping, we'll find that it is the intersection of the input temperaments' mappings, in a similar sense: it includes only the mapping-rows that were in both of their mappings.
In this sense, map-merging and comma-merging should be understood not truly as operations on matrices, but as operations on bases. Another way to describe these such intersections would be as bases for the linear dependence of the given temperaments, as described here: Linear dependence#For a given set of basis matrices, how to compute a basis for their linearly dependent vectors.
-
A map-merge gives a comma-intersection (for purposes of illustrating this concept, the results are not being canonicalized).
-
A comma-merge gives a map-intersection (for purposes of illustrating this concept, the results are not being canonicalized).
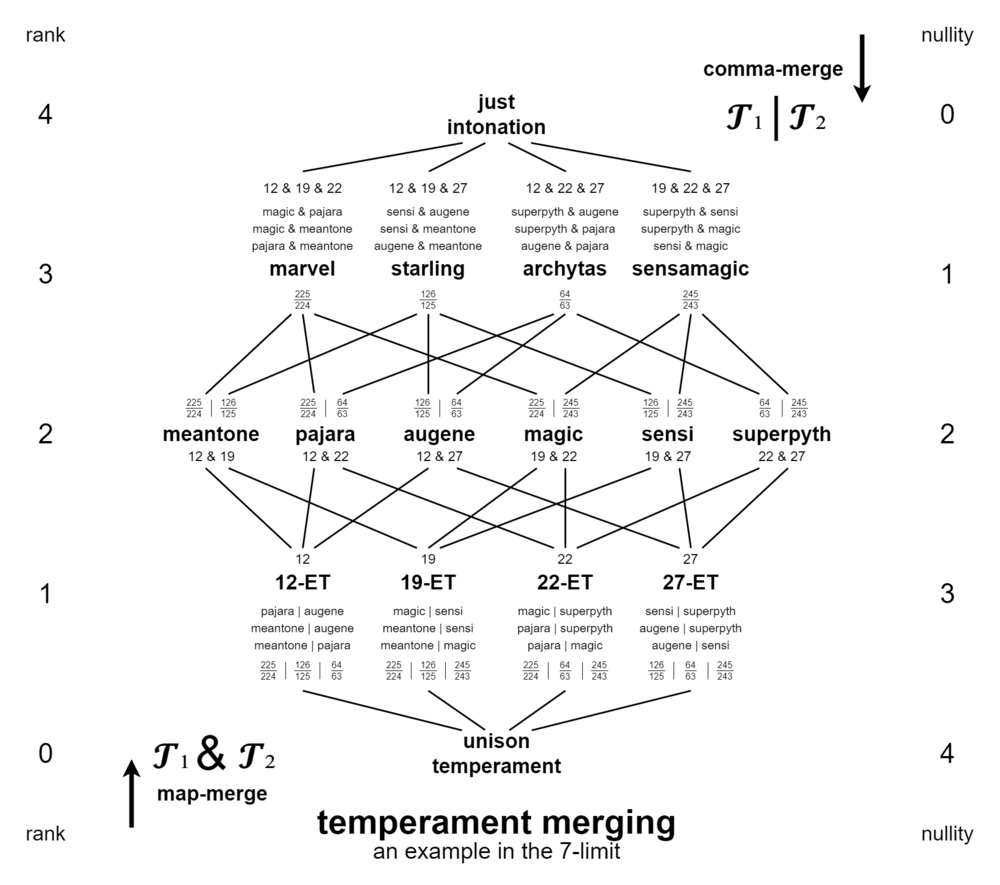
Here we have a group of temperaments that are related by merges. Moving up in this diagram corresponds with map-merges, and downward movement corresponds with comma-merges. Temperaments lower on the chart support ones higher on the chart.
Cross-domain temperament merging
It is possible to merge temperaments from different domains. For more information, see Cross-domain temperament merging.
Wolfram implementation
Temperament merging has been implemented as the functions mapMerge and commaMerge in the RTT library in Wolfram Language.