Wedgie
|
This is a beginner page. It is written to allow new readers to learn about the basics of the topic easily. The corresponding expert page for this topic is Plücker coordinates. |
A wedgie is an object that uniquely characterizes a regular temperament regardless of choice of period vs. generator or of equave, which can therefore provide some illuminating information beyond the mapping matrix, which specifies a particular equave. A wedgie takes the form ⟨⟨…⟨ w1 w2 … wn ]]…], with n entries listed in between multiple val brackets (double brackets for rank-2, triple brackets for rank-3, and so on). Wedgies can be thought of as a generalization of vals, called multivals, so that a val is a wedgie for a rank-1 temperament. Each element conveys information about the structure of a set of primes in the temperament, containing a number of primes equivalent to the temperament's rank.
How to read a wedgie
Following intuitions from ploidacot, one way to characterize a temperament is how many equal parts it splits the perfect fifth (3/2) into. For an example, meantone does not split it at all, so we say it is monocot. We also say it is haploid, since it does not split the octave (2/1) at all.
The elements of a wedgie each represent the number of parts into which a particular subgroup is split by the temperament, or the number of distinct sets of notes within the temperament linked by motions within that subgroup. They can be thought of as a generalization of the ploidacot information to all possible combinations of primes within a temperament, and format that information in a concise manner; as it turns out, this is enough to uniquely characterize the temperament.
For example, take the wedgie for meantone: ⟨⟨ 1 4 4 ]]. Each entry corresponds to a pair of primes: 2.3, 2.5, and 3.5. The first entry of the wedgie is the ploidacot signatures multiplied together, which in this case is 1, telling us that the octave finds 2 at one step, and the fifth finds 3 at one generator minus one octave (which, since there are no even splits, still counts as 1).
For an intuition as to why multiplication is performed, consider hemipyth (or diploid dicot), which divides both the octave and perfect fifth into two parts. In hemipyth, you can use radical steps to traverse between four different "universes" connected by 3-limit intervals: base Pythagorean, offset by a semioctave, offset by a neutral third, and offset by both. The wedgie entry essentially counts these universes.
For 2.5, the procedure generalizes, with the entry, 4, being the number of steps 2 and 5 are divided into respectively multiplied together; that is, the number of parts into which the 2.5 subgroup is split. But since we already know 2 is divided into only one octave, this must mean 5 is split into four parts. In fact, 5 is found at four fifths up.
For the final entry, which is for the 3.5 subgroup, we have another 4. But this time, we are thinking tritave-equivalently now, so we will be reaching 5/3. This is the number of parts 3 and 5/3 are divided into respectively, multiplied together. 3 is reached by going up one 3/2 and one 2/1, but no splitting is happening, so the factor of 4 must come from 5/3, which is indeed reached by four 3/2's.
For another example, take father, which has the wedgie ⟨⟨ 1 -1 -4 ]].
Here, we again have a 1 as our entry for 2.3, meaning that the temperament is haploid monocot, or in other words that 2/1 is unsplit and 3/2 is one generator.
Thus, going into our second entry, -1 for 2.5. Again, since we already know our temperament is haploid, the negative sign must come from the mapping for 5. But what could a negative sign possibly mean in a wedgie? Well, to reach the 5th harmonic (specifically, 5/4) in father, you go up a perfect fourth. Since we are thinking octave-equivalently, this can be seen as going down a perfect fifth.
Finally, for 3.5, we have the entry -4. Again, we are tritave-equivalent and 3/1 is simply found by an octave and a fifth, so we will be finding 5/3 by splitting it into four parts. 5/3 is equated to 16/9 in father, which is found by going up two octaves and down two fifths. This might seem like only a split into two, but keep in mind - we are in tritave-equivalent territory. Octaves are the tritave complement of fifths. So instead of going up two octaves, we can instead simply go down two more fifths to reach 5/3. And there we have it – 5/3 is split into four parts, which each contain a negative generator.
For our final example, we will consider blackwood ⟨⟨ 0 5 8 ]].
Blackwood's first entry is 0, which means that it reduces 2.3 to a rank-1 structure. This can be seen as 3 being found 0 generators from some ploid (since 3/2 in blackwood is 3\5), since 0 times anything is 0.
The next entry, 5, is simple: in 2.5, 5 (in this case, 5/4) is found by going up one generator, but remember that each entry is where the two primes are found multiplied together. Since 2 is found at 5 ploids, the entry is 1 × 5 = 5. (Technically, there is a hidden 5 in the 2.3 entry that gets multiplied by 0 and vanishes.)
And then the final entry, for 3.5, is 8. Again, 5 (i.e. 5/3) is found at one generator, but 3/1 is split into 8 parts by blackwood temperament. So, 1 × 8 = 8.
For wedgies of temperaments of larger prime subgroups, the number of entries is increased, so a rank-2 temperament of 7-limit JI would have 6 entries, for 2.3, 2.5, 2.7, 3.5, 3.7, and 5.7. Note that the new septimal entries are inserted between the entries for the 5-limit. If it helps, think of arranging all the entries in a grid, where rows represent the first prime, and columns represent the second, and reading them off one by one.
For wedgies of higher-rank temperaments, the number of primes per entry is increased, so that for a rank-3 temperament of the 7-limit, all possible combinations of 3 primes (2.3.5, 2.3.7, 2.5.7, and 3.5.7) would be covered.
The form of a wedgie
The notation being used previously, ⟨⟨ x y z ]], is formally a shorthand for a matrix form, written
$$ \begin{bmatrix} 0 & x & y\\ -x & 0 & z\\ -y & -z & 0 \end{bmatrix} $$
For a wedgie on a 4-prime subgroup, the structure of ⟨⟨ a b c d e f ]] is actually
$$ \begin{bmatrix} 0 & a & b & c\\ -a & 0 & d & e\\ -b & -d & 0 & f\\ -c & -e & -f & 0 \end{bmatrix} $$
This means that a wedgie can easily be clipped by removing columns and corresponding rows to produce a restriction of the temperament, and thus wedgies which have a set of entries produced this way in common are strong extensions of some common structure.
Relationship to vals
A val can be seen as a wedgie for a rank-1 temperament (in other words, an equal temperament). Due to being rank-1, there is an entry for each set of 1 prime (or in other words, each prime). This entry can be seen as saying how many parts the prime is split into, which is trivially the number of steps in the equal temperament to reach the prime; in other words, it is the number of "universes" separated by that prime (or more intuitively, pitch classes reduced by that prime) that are reachable by steps in the equal temperament.
Due to this relation, a wedgie is called a multival.
Wedgies and contorsion
|
Todo: expand |
Derivation from mapping matrices
|
|
Todo: expand |
Derivation from edo joins
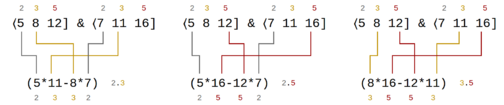
Two vals can be combined into a wedgie representing the rank-2 temperament they both support using the wedge product. For example, wedging ⟨5 8 12] and ⟨7 11 16] (the patent vals for 5edo and 7edo) yields ⟨⟨ (5×11 - 8×7) (5×16 - 12×7) (8×16 - 12×11) ]], which simplifies to ⟨⟨ (55 - 56) (80 - 84) (128 - 132) ]] and thus to ⟨⟨ -1 -4 -4 ]]. Note that we generally assume the first entry of the wedgie should be positive, for which we flip all the signs of it to obtain ⟨⟨ 1 4 4 ]], which is the wedgie for 5 & 7, a.k.a. meantone.
More than two vals can be combined into a higher-rank wedgie by an analogous method.