Temperament merging
This is a beginner page. It is written to allow new readers to learn about the basics of the topic easily.
The corresponding expert page for this topic is Meet and join.
Temperament merging is a way to find new regular temperaments by merging others. There are two ways to merge temperaments: map-merge, which works by merging the temperaments' mappings, and comma-merge, which works by merging the temperaments' comma bases.
Merging
"Merging" in this context refers to concatenating the matrices in question and then canonicalizing them.
For mappings, the concatenation is vertical, while for comma-bases, the concatenation is horizontal:
[math]
\hspace{1cm}
\begin{array} {ccc}
\left[ \begin{array} {rrr}
12 & 19 & 28 \\
\end{array} \right] \\
\text{map-merge} \\
\left[ \begin{array} {rrr}
19 & 30 & 44 \\
\end{array} \right] \\
↓ \\
\left[ \begin{array} {rrr}
12 & 19 & 28 \\
19 & 30 & 44 \\
\end{array} \right] \\
\text{which canonicalizes to} \\
\left[ \begin{array} {rrr}
1 & 0 & -4 \\
0 & 1 & 4 \\
\end{array} \right] \\
\end{array}
\hspace{1cm}
\hspace{1cm}
\left[ \begin{array} {rrr}
-4 \\
4 \\
-1 \\
\end{array} \right]
\text{comma-merge}
\left[ \begin{array} {rrr}
7 \\
0 \\
-3 \\
\end{array} \right]
→
\left[ \begin{array} {rrr}
-4 & 7 \\
4 & 0 \\
-1 & -3 \\
\end{array} \right]
\text{which canonicalizes to}
\left[ \begin{array} {rrr}
-19 & -15 \\
12 & 8 \\
0 & 1 \\
\end{array} \right]
[/math]
Application
Map-merging produces a temperament that only makes to vanish those commas that are made to vanish by all of the input temperaments. Conversely, comma-merging produces a temperament that makes to vanish every comma made to vanish by any of the input temperaments.
For discussions of temperament merging in context, see:
- Dave Keenan & Douglas Blumeyer's guide to RTT
- Diatonic, Chromatic, Enharmonic, Subchromatic#Chromatic and Diatonic Interval Classes
Notation
The & ("ampersand") symbol is used (for example, on Graham Breed's temperament finding tool) to notate map-merging, as in 12&19 = meantone; we can read this as "12-ET and 19-ET is meantone" or "12-ET map-merge 19-ET is meantone". Here, 12 and 19 are wart notation for 12-ET and 19-ET.
The | ("pipe") symbol may be used to notate comma-merging, as in meantone|porcupine = 7. We could read this as "meantone or porcupine" or "meantone comma-merge porcupine is 7-ET". As a mnemonic, because commas are represented by vectors, which are vertical columns, when they merge together into matrices, the pipe resembles the seam between them as they merge.
The & symbol is associated with the word "and", and in many programming languages, the | symbol is associated with the word "or". So a further mnemonic can be used to remember this pair of symbols: [math]𝓣_1 \& 𝓣_2[/math] is the merge that results in the temperament that makes the commas vanish which are made to vanish by both [math]𝓣_1[/math] and [math]𝓣_2[/math], and [math]𝓣_1 | 𝓣_2[/math] is the merge that results in the temperament that makes the commas vanish which are made to vanish by either [math]𝓣_1[/math] or [math]𝓣_2[/math].
Cross-breeding
Perhaps the most basic example of temperament merging is map-merging equal temperaments (ETs), which is sometimes called "cross-breeding". And so meantone could be said to be a cross-breed of 12-ET and 19-ET, because 12&19 = meantone.
Multiple temperament merging
More than two temperaments may be merged at a time, such as 22&34d&37 to give ares.
Non-uniqueness
Note that while a given temperament merging expression unambiguously refers to a single temperament, a given temperament can be expressed by many possible different temperament merging expressions.
Canonicalization
The canonicalization step is important for eliminating any redundancies that may have been introduced by merging related temperaments, such as rank-deficiencies or enfactoring.
Rank-deficiencies
Sometimes when temperaments are merged, rank-deficiencies may occur. For example, comma-merging septimal meantone and miracle temperaments:
[math]
\left[ \begin{array} {r|r}
4 & 13 \\
-4 & -10 \\
1 & 0 \\
0 & 1 \\
\end{array} \right]
|
\left[ \begin{array} {r|r}
-25 & -20 \\
7 & 5 \\
6 & 4 \\
0 & 1 \\
\end{array} \right]
→
\left[ \begin{array} {r|r|r|r}
4 & 13 & -25 & -20 \\
-4 & -10 & 7 & 5 \\
1 & 0 & 6 & 4 \\
0 & 1 & 0 & 1 \\
\end{array} \right]
\text{which in canonical form* is}
\left[ \begin{array} {r|r|r|r}
\style{background-color:#F2B2B4;padding:5px}{0} & -49 & -45 & -36 \\
\style{background-color:#F2B2B4;padding:5px}{0} & 31 & 27 & 21 \\
\style{background-color:#F2B2B4;padding:5px}{0} & 0 & 1 & 0 \\
\style{background-color:#F2B2B4;padding:5px}{0} & 0 & 0 & 1 \\
\end{array} \right]
[/math]
We haven't completely canonicalized yet; we didn't remove the all-zero column (highlighted in red) that was created by the Hermite normal form step. The existence of any all-zero columns like this tells us that our matrix was column-rank-deficient, or in layperson's terms, that it contained redundant commas. In other words, these two temperaments make some of the same commas vanish, and so when we merged them — even though the input temperaments required 2 vectors each to represent — their merged result doesn't require all 4 vectors; it can be completely represented using only 3 vectors. So once we fully canonicalize, any all-zero column(s) are removed, and we end up with:
[math]
\left[ \begin{array} {r|r|r}
-49 & -45 & -36 \\
31 & 27 & 21 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{array} \right]
[/math]
Enfactoring
Sometimes when temperaments are merged, enfactoring may occur. For example:
[math]
\begin{array} {ccc}
\left[ \begin{array} {rrr}
5 & 8 & 12 \\
\end{array} \right] \\
\& \\
\left[ \begin{array} {rrr}
19 & 30 & 44 \\
\end{array} \right] \\
↓ \\
\left[ \begin{array} {rrr}
5 & 8 & 12 \\
19 & 30 & 44 \\
\end{array} \right] \\
\end{array}
[/math]
The greatest factor of this matrix is 2, because we can produce the row ⟨24 38 56] as a coprime linear combination of its rows (that's ⟨5 8 12] + ⟨19 30 44]), and the entries of this row have a GCD of 2, so in other words this matrix is 2-enfactored. If we merely put it into Hermite normal form, we receive:
[math]
\left[ \begin{array} {rrr}
1 & 0 & -4 \\
0 & 2 & 8 \\
\end{array} \right]
[/math]
which is a 2-enfactored meantone mapping, and it reveals the greatest factor as the GCD of the second row. But if we fully canonicalize it (defactor, and put into normal form), then we get:
[math]
\left[ \begin{array} {rrr}
1 & 0 & -4 \\
0 & 1 & 4 \\
\end{array} \right]
[/math]
which is simply the canonical mapping for meantone temperament.
Non-canonicalizing definition
By some definitions of the & operator, the defactoring part of canonicalization is not included — for example on Graham Breed's temperament finding tool. This allows for things like 5&19 to represent 2-enfactored meantone, rather than meantone itself. Instead of a full canonicalization, then, this definition merely puts the result into Hermite normal form and removes any all-zero rows or columns resulting from rank-deficiencies.
Parallel intersections
Every temperament mapping has a dual comma basis, and every comma basis has a dual mapping. Because of this duality, a special parallelism exists.
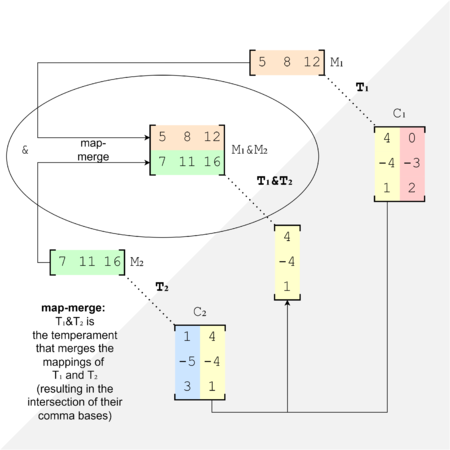
If we perform a map-merge, then look at the resultant mapping's comma basis, we'll find that it is the intersection of the input temperaments' comma bases. In other words, and like stated earlier, it includes only the commas that were in both of their comma bases.
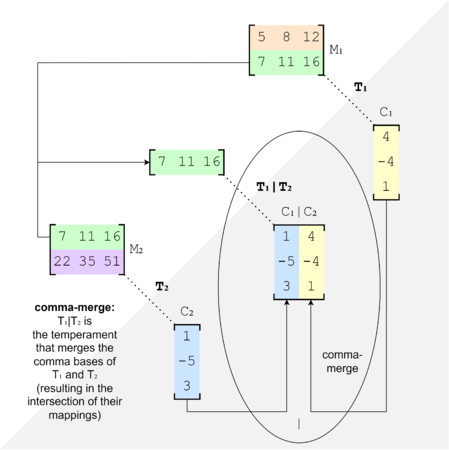
Similarly, if we perform a comma-merge, then look at the resultant comma basis's mapping, we'll find that it is the intersection of the input temperaments' mappings, in a similar sense: it includes only the mapping-rows that were in both of their mappings.
In this sense, map-merging and comma-merging should be understood not truly as operations on matrices, but as operations on bases. Another way to describe these such intersections would be as bases for the linear dependence of the given temperaments, as described here: Linear dependence#For a given set of basis matrices, how to compute a basis for their linearly dependent vectors.
A map-merge gives a comma-intersection (for purposes of illustrating this concept, the results are not being canonicalized).
A comma-merge gives a map-intersection (for purposes of illustrating this concept, the results are not being canonicalized).
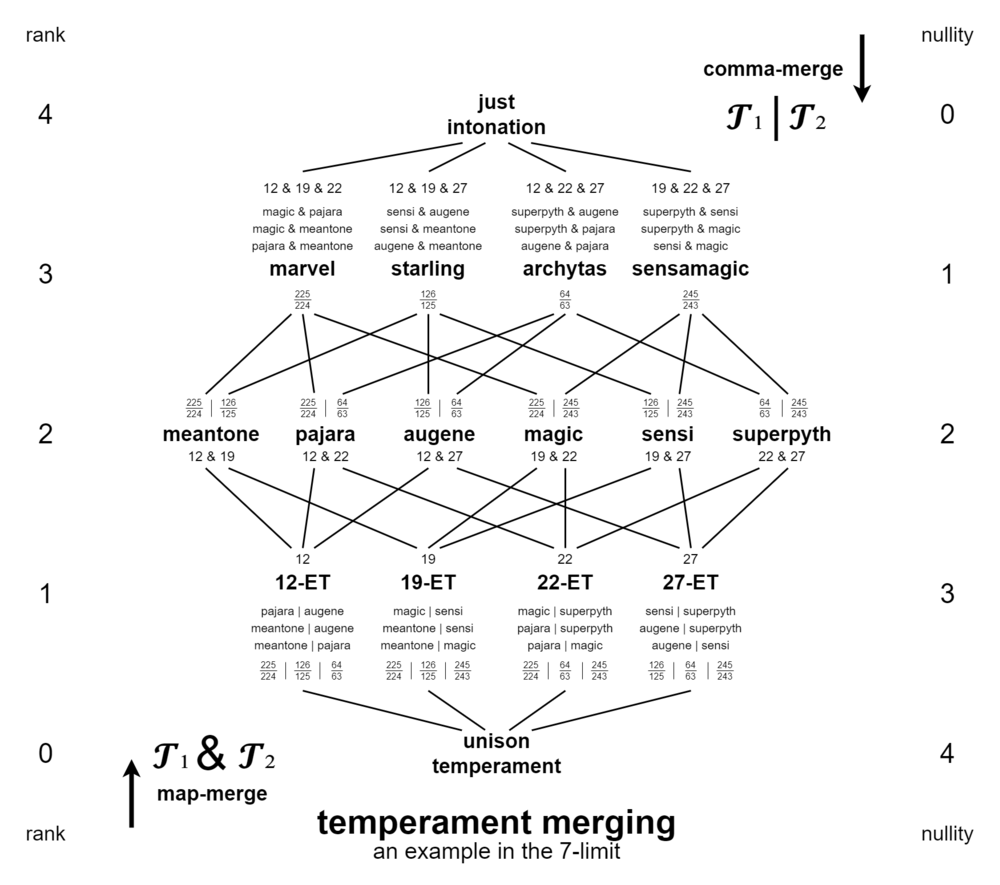
Here we have a group of temperaments that are related by merges. Moving up in this diagram corresponds with map-merges, and downward movement corresponds with comma-merges. Temperaments lower on the chart support ones higher on the chart.
Vs. the wedge product
Temperament merging is closely related to the wedge product. For more information, see: Douglas Blumeyer and Dave Keenan's Intro to exterior algebra for RTT#Temperament merging.
Cross-domain temperament merging
It is possible to merge temperaments from different domains. For more information, see Cross-domain temperament merging.
Wolfram implementation
Temperament merging has been implemented as the functions mapMerge and commaMerge in the RTT library in Wolfram Language.