12edo
12edo, perhaps better known as 12et since it really is a temperament, is the predominating tuning system in the world today. It achieved that position because it is the smallest equal division of the octave (EDO) which can seriously claim to represent 5-limit harmony, and because as 1/12 Pythagorean comma (approximately 1/11 syntonic comma or full schisma) meantone, it represents meantone.
It divides the octave into twelve equal parts, each of exactly 100 cents each unless octave shrinking or stretching is employed. Its has a fifth which is quite good at two cents flat. It has a major third which is 13+2/3 cents sharp, which works well enough for some styles of music and is not really adequate for others, and a minor third which is flat by even more, 15+2/3 cents. It is probably not an accident that as tuning in European music became increasingly close to 12et, the style of the music changed so that the defects of 12et appeared less evident, though it should be borne in mind that in actual performance these are often reduced by the tuning adaptations of the performers.
The seventh partial (7/4) is "represented" by an interval which is sharp by over 31 cents, and stands out distinctly from the rest of the chord in a tetrad. Such tetrads are often being used as dominant seventh chords in functional harmony, for which the 5-limit JI version would be 1/1 - 5/4 - 3/2 - 16/9, and while 12et officially supports septimal meantone via the val <12 19 28 34|, its credentials in the 7-limit department are distinctly cheesy. It cannot be said to represent 11 or 13 at all, though it does a quite credible 17 and an even better 19. Nevertheless its relative tuning accuracy is quite high, and 12edo is the fourth zeta integral edo.
In terms of the kernel, which is to say the commas it tempers out, it tempers out the Pythagorean comma, 3^12/2^19, the Didymus comma, 81/80, the diesis, 128/125, the diaschisma, 2048/2025, the Archytas comma, 64/63, the septimal quartertone, 36/35, the jubilisma, 50/49, the septimal semicomma, 126/125, and the septimal kleisma, 225/224. Each of these affects the structure of 12et in specific ways, and tuning systems which share the comma in question will be similar to 12et in precisely those ways.
Intervals
| Degree | Cents | Interval | 7-limit Ratios* | ||
|---|---|---|---|---|---|
| 0 | 0 | unison | P1 | D | 1/1 |
| 1 | 100 | aug 1sn, minor 2nd | A1, m2 | D#, Eb | 15/14, 16/15, 21/20, 25/24, 28/27 |
| 2 | 200 | major 2nd | M2 | E | 8/7, 9/8, 10/9 |
| 3 | 300 | minor 3rd | m3 | F | 7/6, 6/5 |
| 4 | 400 | major 3rd | M3 | F# | 5/4, 9/7 |
| 5 | 500 | perfect 4th | P4 | G | 4/3 |
| 6 | 600 | aug 4th, dim 5th | A4, d5 | G#, Ab | 7/5, 10/7 |
| 7 | 700 | perfect 5th | P5 | A | 3/2 |
| 8 | 800 | minor 6th | m6 | Bb | 8/5, 14/9 |
| 9 | 900 | major 6th | M6 | B | 5/3, 12/7 |
| 10 | 1000 | minor 7th | m7 | C | 7/4, 9/5, 16/9 |
| 11 | 1100 | major 7th | M7 | C# | 15/8, 28/15, 40/21, 48/25, 27/14 |
| 19 | 1200 | perfect 8ve | P8 | D | 2/1 |
* based on treating 12-edo as a 2.3.5.7 subgroup temperament; other approaches are possible.
Rank two temperaments
- List of 12et rank two temperaments by badness
- List of 12et rank two temperaments by complexity
- List of edo-distinct 12f rank two temperaments
| Periods per octave |
Generator | Temperaments |
|---|---|---|
| 1 | 1\12 | Ripple |
| 1 | 5\12 | Meantone/dominant |
| 2 | 1\12 | Srutal/pajara/injera |
| 3 | 1\12 | Augmented |
| 4 | 1\12 | Diminished |
| 6 | 1\12 | Hexe |
Commas
12 EDO tempers out the following commas. (Note: This assumes val < 12 19 28 34 42 44 |.)
| Rational | Monzo | Cents | Color Name | Name 1 | Name 2 | Name 3 |
|---|---|---|---|---|---|---|
| 648/625 | [3 4 -4⟩ | 62.57 | Quadgu | Major Diesis | Diminished Comma | |
| 36/35 | [2 2 -1 -1⟩ | 48.77 | Rugu | Septimal Quarter Tone | ||
| 128/125 | [7 0 -3⟩ | 41.06 | Trigu | Diesis | Augmented Comma | |
| 50/49 | [1 0 2 -2⟩ | 34.98 | Biruyo | Tritonic Diesis | Jubilisma | |
| 64/63 | [6 -2 0 -1⟩ | 27.26 | Ru | Septimal Comma | Archytas' Comma | Leipziger Komma |
| 531441/524288 | [-19 12⟩ | 23.46 | Lalawa | Pythagorean Comma | ||
| 81/80 | [-4 4 -1⟩ | 21.51 | Gu | Syntonic Comma | Didymos Comma | Meantone Comma |
| 3125/3087 | [0 -2 5 -3⟩ | 21.18 | Triru-aquinyo | Gariboh | ||
| 2048/2025 | [11 -4 -2⟩ | 19.55 | Sagugu | Diaschisma | ||
| 91/90 | [-1 -2 -1 1 0 1⟩ | 19.13 | Thozogu | Superleap | ||
| 5201701/5149091 | [26 -12 -3⟩ | 17.60 | Sasa-trigu | Misty Comma | ||
| 99/98 | [-1 2 0 -2 1⟩ | 17.58 | Loruru | Mothwellsma | ||
| 100/99 | [2 -2 2 0 -1⟩ | 17.40 | Luyoyo | Ptolemisma | ||
| 126/125 | [1 2 -3 1⟩ | 13.79 | Zotrigu | Septimal Semicomma | Starling Comma | |
| 4000/3969 | [5 -4 3 -2⟩ | 13.47 | Rurutriyo | Octagar | ||
| 176/175 | [4 0 -2 -1 1⟩ | 9.86 | Lorugugu | Valinorsma | ||
| 896/891 | [7 -4 0 1 -1⟩ | 9.69 | Saluzo | Pentacircle | ||
| 321489/320000 | [-9 8 -4 2⟩ | 8.04 | Labizogugu | Varunisma | ||
| 225/224 | [-5 2 2 -1⟩ | 7.71 | Ruyoyo | Septimal Kleisma | Marvel Comma | |
| 3136/3125 | [6 0 -5 2⟩ | 6.08 | Zozoquingu | Hemimean | ||
| 5120/5103 | [10 -6 1 -1⟩ | 5.76 | Saruyo | Hemifamity | ||
| 441/440 | [-3 2 -1 2 -1⟩ | 3.93 | Luzozogu | Werckisma | ||
| 33554432/33480783 | [25 -14 0 -1⟩ | 3.80 | Sasaru | Garischisma | ||
| 32805/32768 | [-15 8 1⟩ | 1.95 | Layo | Schisma | ||
| 703125/702464 | [-11 2 7 -3⟩ | 1.63 | Latriru-asepyo | Meter | ||
| 250047/250000 | [-4 6 -6 3⟩ | 0.33 | Trizogugu | Landscape Comma | ||
| 9801/9800 | [-3 4 -2 -2 2⟩ | 0.18 | Bilorugu | Kalisma | Gauss' Comma | |
| [161 -84 -12⟩ | 0.02 | Sepbisa-quadtrigu | Atom |
Scales
Intervals
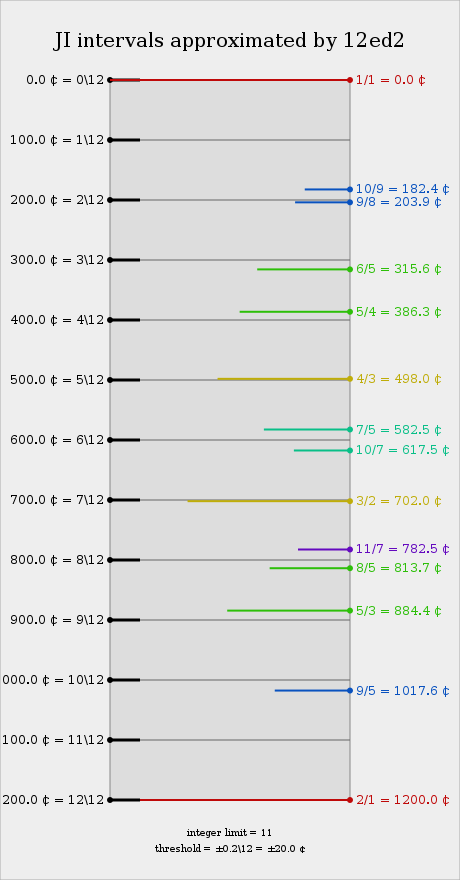
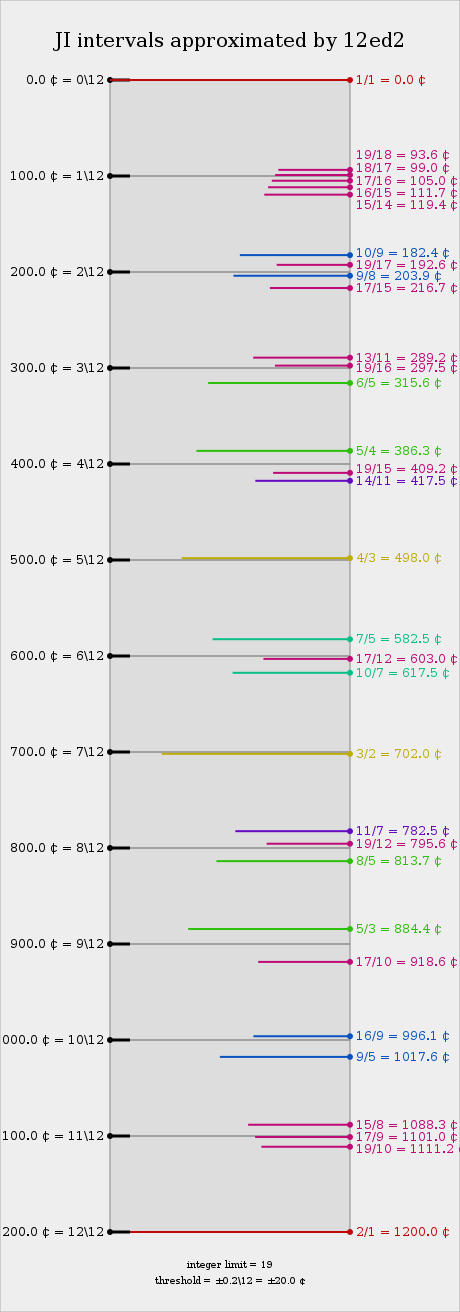
An expanded version of the above, including some higher-limit intervals:
Selected just intervals by error
The following table shows how some prominent just intervals are represented in 12edo (ordered by absolute error).
| Interval, complement | Error (abs., in cents) |
|---|---|
| 4/3, 3/2 | 1.955 |
| 15/13, 26/15 | 2.259 |
| 9/8, 16/9 | 3.910 |
| 13/11, 22/13 | 10.790 |
| 16/15, 15/8 | 11.731 |
| 5/4, 8/5 | 13.686 |
| 6/5, 5/3 | 15.641 |
| 7/5, 10/7 | 17.488 |
| 14/11, 11/7 | 17.508 |
| 10/9, 9/5 | 17.596 |
| 15/14, 28/15 | 19.443 |
| 14/13, 13/7 | 28.298 |
| 8/7, 7/4 | 31.174 |
| 7/6, 12/7 | 33.129 |
| 11/10, 20/11 | 34.996 |
| 9/7, 14/9 | 35.084 |
| 18/13, 13/9 | 36.618 |
| 15/11, 22/15 | 36.951 |
| 13/12, 24/13 | 38.573 |
| 16/13, 13/8 | 40.528 |
| 13/10, 20/13 | 45.786 |
| 11/9, 18/11 | 47.408 |
| 11/8, 16/11 | 48.682 |
| 12/11, 11/6 | 49.323 |