|
|
| Line 1: |
Line 1: |
| <h2>IMPORTED REVISION FROM WIKISPACES</h2>
| | The keenanisma is the 11-limit comma 385/384 = |-7 -1 1 1 1> of 4.503 cents. Tempering it out leads to the 11-limit rank four [[Keenanismic_family|keenanismic temperament]]. |
| This is an imported revision from Wikispaces. The revision metadata is included below for reference:<br>
| |
| : This revision was by author [[User:phylingual|phylingual]] and made on <tt>2012-07-25 17:50:56 UTC</tt>.<br>
| |
| : The original revision id was <tt>354810156</tt>.<br>
| |
| : The revision comment was: <tt></tt><br>
| |
| The revision contents are below, presented both in the original Wikispaces Wikitext format, and in HTML exactly as Wikispaces rendered it.<br>
| |
| <h4>Original Wikitext content:</h4>
| |
| <div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;white-space: pre-wrap ! important" class="old-revision-html">The keenanisma is the 11-limit comma 385/384 = |-7 -1 1 1 1> of 4.503 cents. Tempering it out leads to the 11-limit rank four [[Keenanismic family|keenanismic temperament]].
| |
|
| |
|
| The keenanisma equates 48/35 with 11/8 and 35/24 with 16/11; these are 7-limit intervals of low complexity, lying across from 1/1 in the hexanies 8/7-6/5-48/35-8/5-12/7-2 and 7/6-5/4-35/24-5/3-7/4-2. Hence keenanismic tempering allows the hexany to be viewed as containing some 11-limit harmony. The hexany is a fundamental construct in the 3D lattice of [[The Seven Limit Symmetrical Lattices|7-limit pitch classes]], the "deep holes" of the lattice as opposed to the "holes" represented by major and minor tetrads, and in terms of the [[The Seven Limit Symmetrical Lattices|cubic lattice of 7-limit tetrads]], the otonal tetrad with root 11 (or 11/8) is represented by [-2 0 0]: 1-6/5-48/35-12/7-2. In terms of 7-limit chord relationships, this complexity is as low as possible for an 11-limit projection comma, equaling the [0 1 -1] of 56/55 and less than the other alternatives. Since keenanismic temperament is also quite accurate, this singles it out as being of special interest. | | The keenanisma equates 48/35 with 11/8 and 35/24 with 16/11; these are 7-limit intervals of low complexity, lying across from 1/1 in the hexanies 8/7-6/5-48/35-8/5-12/7-2 and 7/6-5/4-35/24-5/3-7/4-2. Hence keenanismic tempering allows the hexany to be viewed as containing some 11-limit harmony. The hexany is a fundamental construct in the 3D lattice of [[The_Seven_Limit_Symmetrical_Lattices|7-limit pitch classes]], the "deep holes" of the lattice as opposed to the "holes" represented by major and minor tetrads, and in terms of the [[The_Seven_Limit_Symmetrical_Lattices|cubic lattice of 7-limit tetrads]], the otonal tetrad with root 11 (or 11/8) is represented by [-2 0 0]: 1-6/5-48/35-12/7-2. In terms of 7-limit chord relationships, this complexity is as low as possible for an 11-limit projection comma, equaling the [0 1 -1] of 56/55 and less than the other alternatives. Since keenanismic temperament is also quite accurate, this singles it out as being of special interest. |
|
| |
|
| EDOs with [[patent val]]s tempering out the keenansima include [[15edo|15]], [[19edo|19]], [[22edo|22]], [[31edo|31]], [[34edo|34]], [[37edo|37]], [[41edo|41]], [[53edo|53]], [[68edo|68]], [[72edo|72]], [[118edo|118]], [[159edo|159]], [[190edo|190]], [[212edo|212]] and [[284edo|284]]. | | EDOs with [[Patent_val|patent val]]s tempering out the keenansima include [[15edo|15]], [[19edo|19]], [[22edo|22]], [[31edo|31]], [[34edo|34]], [[37edo|37]], [[41edo|41]], [[53edo|53]], [[68edo|68]], [[72edo|72]], [[118edo|118]], [[159edo|159]], [[190edo|190]], [[212edo|212]] and [[284edo|284]]. |
|
| |
|
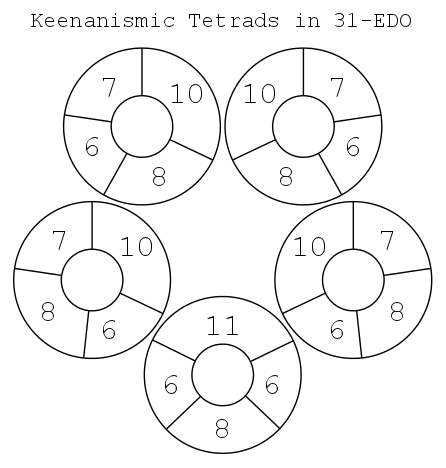
| Characteristic of keenanismic tempering are the [[keenanismic tetrads]], 385/384-tempered versions of 1-5/4-3/2-12/7, 1-5/4-10/7-12/7, 1-6/5-3/2-7/4, 1-5/4-16/11-7/4, and 1-14/11-16/11-7/4. These are essentially tempered [[dyadic chord]]s, where every dyad of the chord is a keenanismic tempered version of an interval of the 11-limit [[tonality diamond]], and hence regarded as an 11-limit consonance. | | Characteristic of keenanismic tempering are the [[keenanismic_tetrads|keenanismic tetrads]], 385/384-tempered versions of 1-5/4-3/2-12/7, 1-5/4-10/7-12/7, 1-6/5-3/2-7/4, 1-5/4-16/11-7/4, and 1-14/11-16/11-7/4. These are essentially tempered [[Dyadic_chord|dyadic chord]]s, where every dyad of the chord is a keenanismic tempered version of an interval of the 11-limit [[Tonality_diamond|tonality diamond]], and hence regarded as an 11-limit consonance. |
|
| |
|
| [[image:keenanismic_tetrads_in_31edo_sym.png]]</pre></div> | | [[File:keenanismic_tetrads_in_31edo_sym.png|alt=keenanismic_tetrads_in_31edo_sym.png|keenanismic_tetrads_in_31edo_sym.png]] [[Category:11-limit]] |
| <h4>Original HTML content:</h4>
| | [[Category:31edo]] |
| <div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;width:200%;white-space: pre-wrap ! important" class="old-revision-html"><html><head><title>385_384</title></head><body>The keenanisma is the 11-limit comma 385/384 = |-7 -1 1 1 1&gt; of 4.503 cents. Tempering it out leads to the 11-limit rank four <a class="wiki_link" href="/Keenanismic%20family">keenanismic temperament</a>.<br />
| | [[Category:comma]] |
| <br />
| | [[Category:keenanismic]] |
| The keenanisma equates 48/35 with 11/8 and 35/24 with 16/11; these are 7-limit intervals of low complexity, lying across from 1/1 in the hexanies 8/7-6/5-48/35-8/5-12/7-2 and 7/6-5/4-35/24-5/3-7/4-2. Hence keenanismic tempering allows the hexany to be viewed as containing some 11-limit harmony. The hexany is a fundamental construct in the 3D lattice of <a class="wiki_link" href="/The%20Seven%20Limit%20Symmetrical%20Lattices">7-limit pitch classes</a>, the &quot;deep holes&quot; of the lattice as opposed to the &quot;holes&quot; represented by major and minor tetrads, and in terms of the <a class="wiki_link" href="/The%20Seven%20Limit%20Symmetrical%20Lattices">cubic lattice of 7-limit tetrads</a>, the otonal tetrad with root 11 (or 11/8) is represented by [-2 0 0]: 1-6/5-48/35-12/7-2. In terms of 7-limit chord relationships, this complexity is as low as possible for an 11-limit projection comma, equaling the [0 1 -1] of 56/55 and less than the other alternatives. Since keenanismic temperament is also quite accurate, this singles it out as being of special interest.<br />
| | [[Category:tetrad]] |
| <br />
| |
| EDOs with <a class="wiki_link" href="/patent%20val">patent val</a>s tempering out the keenansima include <a class="wiki_link" href="/15edo">15</a>, <a class="wiki_link" href="/19edo">19</a>, <a class="wiki_link" href="/22edo">22</a>, <a class="wiki_link" href="/31edo">31</a>, <a class="wiki_link" href="/34edo">34</a>, <a class="wiki_link" href="/37edo">37</a>, <a class="wiki_link" href="/41edo">41</a>, <a class="wiki_link" href="/53edo">53</a>, <a class="wiki_link" href="/68edo">68</a>, <a class="wiki_link" href="/72edo">72</a>, <a class="wiki_link" href="/118edo">118</a>, <a class="wiki_link" href="/159edo">159</a>, <a class="wiki_link" href="/190edo">190</a>, <a class="wiki_link" href="/212edo">212</a> and <a class="wiki_link" href="/284edo">284</a>.<br />
| |
| <br />
| |
| Characteristic of keenanismic tempering are the <a class="wiki_link" href="/keenanismic%20tetrads">keenanismic tetrads</a>, 385/384-tempered versions of 1-5/4-3/2-12/7, 1-5/4-10/7-12/7, 1-6/5-3/2-7/4, 1-5/4-16/11-7/4, and 1-14/11-16/11-7/4. These are essentially tempered <a class="wiki_link" href="/dyadic%20chord">dyadic chord</a>s, where every dyad of the chord is a keenanismic tempered version of an interval of the 11-limit <a class="wiki_link" href="/tonality%20diamond">tonality diamond</a>, and hence regarded as an 11-limit consonance.<br />
| |
| <br />
| |
| <!-- ws:start:WikiTextLocalImageRule:0:&lt;img src=&quot;/file/view/keenanismic_tetrads_in_31edo_sym.png/354772590/keenanismic_tetrads_in_31edo_sym.png&quot; alt=&quot;&quot; title=&quot;&quot; /&gt; --><img src="/file/view/keenanismic_tetrads_in_31edo_sym.png/354772590/keenanismic_tetrads_in_31edo_sym.png" alt="keenanismic_tetrads_in_31edo_sym.png" title="keenanismic_tetrads_in_31edo_sym.png" /><!-- ws:end:WikiTextLocalImageRule:0 --></body></html></pre></div>
| |
The keenanisma is the 11-limit comma 385/384 = |-7 -1 1 1 1> of 4.503 cents. Tempering it out leads to the 11-limit rank four keenanismic temperament.
The keenanisma equates 48/35 with 11/8 and 35/24 with 16/11; these are 7-limit intervals of low complexity, lying across from 1/1 in the hexanies 8/7-6/5-48/35-8/5-12/7-2 and 7/6-5/4-35/24-5/3-7/4-2. Hence keenanismic tempering allows the hexany to be viewed as containing some 11-limit harmony. The hexany is a fundamental construct in the 3D lattice of 7-limit pitch classes, the "deep holes" of the lattice as opposed to the "holes" represented by major and minor tetrads, and in terms of the cubic lattice of 7-limit tetrads, the otonal tetrad with root 11 (or 11/8) is represented by [-2 0 0]: 1-6/5-48/35-12/7-2. In terms of 7-limit chord relationships, this complexity is as low as possible for an 11-limit projection comma, equaling the [0 1 -1] of 56/55 and less than the other alternatives. Since keenanismic temperament is also quite accurate, this singles it out as being of special interest.
EDOs with patent vals tempering out the keenansima include 15, 19, 22, 31, 34, 37, 41, 53, 68, 72, 118, 159, 190, 212 and 284.
Characteristic of keenanismic tempering are the keenanismic tetrads, 385/384-tempered versions of 1-5/4-3/2-12/7, 1-5/4-10/7-12/7, 1-6/5-3/2-7/4, 1-5/4-16/11-7/4, and 1-14/11-16/11-7/4. These are essentially tempered dyadic chords, where every dyad of the chord is a keenanismic tempered version of an interval of the 11-limit tonality diamond, and hence regarded as an 11-limit consonance.