23edo: Difference between revisions
m →Intervals: style |
added color names to the comma list, general cleanup |
||
| Line 7: | Line 7: | ||
----- | ----- | ||
= | =Theory= | ||
<b>23-TET</b>, or <b>23-EDO</b>, is a tempered musical system which divides the [[Octave|octave]] into 23 equal parts of approximately 52.173913 cents, which is also called with the neologism Icositriphony ''(Icositrifonía)''. It has good approximations for [[5/3|5/3]], [[11/7|11/7]], 13 and 17, allowing it to represent the 2.5/3.11/7.13.17 [[just_intonation_subgroup|just intonation subgroup]]. If to this subgroup is added the commas of [[17-limit|17-limit]] [[46edo|46edo]], the larger 17-limit [[k*N_subgroups|2*23 subgroup]] 2.9.15.21.33.13.17 is obtained. This is the largest subgroup on which 23 has the same tuning and commas as does 17-limit·46edo, and may be regarded as a basis for analyzing the harmony of 23-EDO so far, as approximations to just intervals goes. 23edo is the 9th [[prime_numbers|prime]] edo, following [[19edo|19edo]] and coming before [[29edo|29edo]]. | <b>23-TET</b>, or <b>23-EDO</b>, is a tempered musical system which divides the [[Octave|octave]] into 23 equal parts of approximately 52.173913 cents, which is also called with the neologism Icositriphony ''(Icositrifonía)''. It has good approximations for [[5/3|5/3]], [[11/7|11/7]], 13 and 17, allowing it to represent the 2.5/3.11/7.13.17 [[just_intonation_subgroup|just intonation subgroup]]. If to this subgroup is added the commas of [[17-limit|17-limit]] [[46edo|46edo]], the larger 17-limit [[k*N_subgroups|2*23 subgroup]] 2.9.15.21.33.13.17 is obtained. This is the largest subgroup on which 23 has the same tuning and commas as does 17-limit·46edo, and may be regarded as a basis for analyzing the harmony of 23-EDO so far, as approximations to just intervals goes. 23edo is the 9th [[prime_numbers|prime]] edo, following [[19edo|19edo]] and coming before [[29edo|29edo]]. | ||
23-EDO was proposed by ethnomusicologist [http://en.wikipedia.org/wiki/Erich_von_Hornbostel Erich von Hornbostel] as the result of continuing a circle of "blown" fifths of ~678-cent fifths that (he argued) resulted from "overblowing" a bamboo pipe. | |||
23-EDO is also significant in that it is the largest EDO that fails to approximate the 3rd, 5th, 7th, and 11th harmonics within 20 cents, which makes it well-suited for musicians seeking to explore harmonic territory that is unusual even for the average microtonalist. Oddly, despite the fact that it fails to approximate these harmonics, it approximates the intervals between them (5/3, 7/3, 11/3, 7/5, 11/7, and 11/5) very well. The lowest harmonics well-approximated by 23-EDO are 13, 17, 21, and 23. See [[Harmony_of_23edo|here]] for more details. Also note that some approximations can be improved by [[23edo_and_octave_stretching|octave stretching]]. | |||
As with[[9edo| 9-EDO]], [[16edo|16-EDO]], and [[25edo|25-EDO]], one way to treat 23-EDO is as a Pelogic temperament, tempering out the "comma" of 135/128 and equating three 'acute [[4/3|4/3]]'s with 5/1 (related to the Armodue system). This means mapping '[[3/2|3/2]]' to 13 degrees of 23, and results in a 7 notes [[2L_5s|Anti-diatonic scale]] of 3 3 4 3 3 3 4 (in steps of 23-EDO), which extends to 9 notes [[7L_2s|Superdiatonic scale]] (3 3 3 1 3 3 3 3 1). One can notate 23-EDO using the Armodue system, but just like notating 17-EDO with familiar diatonic notation, flats will be lower in pitch than enharmonic sharps, because in 23-EDO, the "Armodue 6th" is sharper than it is in 16-EDO, just like the Diatonic 5th in 17-EDO is sharper than in 12-EDO. In other words, 2b is lower in pitch than 1#, just like how in 17-EDO, Eb is lower than D#. | |||
[[ | However, one can also map 3/2 to 14 degrees of 23-EDO without significantly increasing the error, taking us to a [[7-limit|7-limit]] temperament where two 'broad 3/2's equals 7/3, meaning 28/27 is tempered out, and six 4/3's octave-reduced equals 5/4, meaning 4096/3645 is tempered out. Both of these are very large commas, so this is not at all an accurate temperament, but it is related to [[13edo|13-EDO]] and [[18edo|18-EDO]] and produces [[MOSScales|MOS scales]] of 5 and 8 notes: 5 5 4 5 4 (the [[3L_2s|"anti-pentatonic"]]) and 4 1 4 1 4 4 1 4 (the "quarter-tone" version of the Blackwood/[http://en.wikipedia.org/wiki/Paul_Rapoport_%28music_critic%29 Rapoport]/Wilson 13-EDO "subminor" scale). Alternatively we can treat this temperament as a 2.9.21 subgroup, and instead of calling 9 degrees of 23-EDO a Sub-"4/3", we can call it 21/16. Here three 21/16's gets us to 9/4, meaning 1029/1024 is tempered out. This allows us to treat a triad of 0-4-9 degrees of 23-EDO as an approximation to 16:18:21, and 0-5-9 as 1/(16:18:21); both of these triads are abundant in the 8-note MOS scale. | ||
=Notation= | |||
23edo can be notated with conventional notation, including the staff, note names, relative notation, etc. in two ways. The first preserves the <u>melodic</u> meaning of sharp/flat, major/minor and aug/dim, in that sharp is higher pitched than flat, and major/aug is wider than minor/dim. The disadvantage to this approach is that conventional interval arithmetic no longer works. e.g. M2 + M2 isn't M3, and D + M2 isn't E. Chord names are different because C - E - G isn't P1 - M3 - P5. | 23edo can be notated with conventional notation, including the staff, note names, relative notation, etc. in two ways. The first preserves the <u>melodic</u> meaning of sharp/flat, major/minor and aug/dim, in that sharp is higher pitched than flat, and major/aug is wider than minor/dim. The disadvantage to this approach is that conventional interval arithmetic no longer works. e.g. M2 + M2 isn't M3, and D + M2 isn't E. Chord names are different because C - E - G isn't P1 - M3 - P5. | ||
| Line 281: | Line 286: | ||
<ul><li>The dots indicate which frets on a 23-edo guitar would have dots.<ul><li>Based on treating 23-EDO as a 2.9.15.21.33.13.17 subgroup temperament; other approaches are possible.</li></ul></li></ul> | <ul><li>The dots indicate which frets on a 23-edo guitar would have dots.<ul><li>Based on treating 23-EDO as a 2.9.15.21.33.13.17 subgroup temperament; other approaches are possible.</li></ul></li></ul> | ||
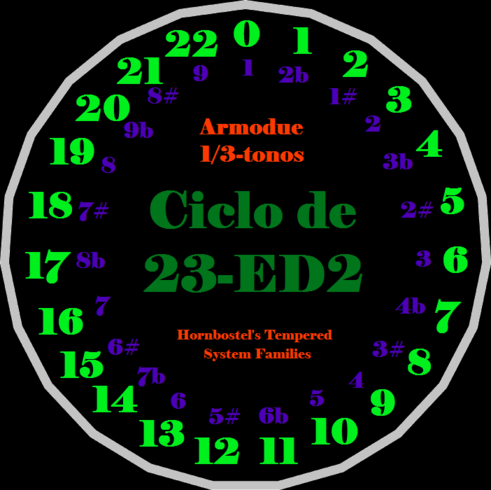
=== Armodue Notation === | |||
[[File:Ciclo_Icositrifonía.png|alt=Ciclo Icositrifonía.png|491x490px|link=Harmony_of_23edo]] | |||
== | |||
[ | |||
[ | |||
=Commas= | =Commas= | ||
23 EDO tempers out the following commas. (Note: This assumes the val < 23 36 53 65 80 85 |.) Also note the discussion above, where there are some commas mentioned that are not in the standard comma list (e.g., 28/27). | 23 EDO tempers out the following [[commas]]. (Note: This assumes the val < 23 36 53 65 80 85 |.) Also note the discussion above, where there are some commas mentioned that are not in the standard comma list (e.g., 28/27). | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
! | | ! | [[Ratio]] | ||
! | Monzo | ! | [[Monzo]] | ||
! | | ! | [[Cents]] | ||
![[Color notation/Temperament Names|Color Name]] | |||
! | Name 1 | ! | Name 1 | ||
! | Name 2 | ! | Name 2 | ||
| Line 384: | Line 305: | ||
| |<nowiki> | -7 3 1 </nowiki>> | | |<nowiki> | -7 3 1 </nowiki>> | ||
| style="text-align:right;" | 92.18 | | style="text-align:right;" | 92.18 | ||
| style="text-align:center;" |Layobi | |||
| style="text-align:center;" | Major Chroma | | style="text-align:center;" | Major Chroma | ||
| style="text-align:center;" | Major Limma | | style="text-align:center;" | Major Limma | ||
| Line 391: | Line 313: | ||
| |<nowiki> | -6 -5 6 </nowiki>> | | |<nowiki> | -6 -5 6 </nowiki>> | ||
| style="text-align:right;" | 8.11 | | style="text-align:right;" | 8.11 | ||
| style="text-align:center;" |Tribiyo | |||
| style="text-align:center;" | Kleisma | | style="text-align:center;" | Kleisma | ||
| style="text-align:center;" | Semicomma Majeur | | style="text-align:center;" | Semicomma Majeur | ||
| Line 398: | Line 321: | ||
| |<nowiki> | 2 2 -1 -1 </nowiki>> | | |<nowiki> | 2 2 -1 -1 </nowiki>> | ||
| style="text-align:right;" | 48.77 | | style="text-align:right;" | 48.77 | ||
| style="text-align:center;" |Rugu | |||
| style="text-align:center;" | Septimal Quarter Tone | | style="text-align:center;" | Septimal Quarter Tone | ||
| style="text-align:center;" | | | style="text-align:center;" | | ||
| Line 405: | Line 329: | ||
| |<nowiki> | -9 1 2 1 </nowiki>> | | |<nowiki> | -9 1 2 1 </nowiki>> | ||
| style="text-align:right;" | 43.41 | | style="text-align:right;" | 43.41 | ||
| style="text-align:center;" |Lazoyoyo | |||
| style="text-align:center;" | Avicennma | | style="text-align:center;" | Avicennma | ||
| style="text-align:center;" | Avicenna's Enharmonic Diesis | | style="text-align:center;" | Avicenna's Enharmonic Diesis | ||
| Line 412: | Line 337: | ||
| |<nowiki> | 5 -4 3 -2 </nowiki>> | | |<nowiki> | 5 -4 3 -2 </nowiki>> | ||
| style="text-align:right;" | 13.47 | | style="text-align:right;" | 13.47 | ||
| style="text-align:center;" |Rurutriyo | |||
| style="text-align:center;" | Octagar | | style="text-align:center;" | Octagar | ||
| style="text-align:center;" | | | style="text-align:center;" | | ||
| Line 419: | Line 345: | ||
| |<nowiki> | 11 1 -3 -2 </nowiki>> | | |<nowiki> | 11 1 -3 -2 </nowiki>> | ||
| style="text-align:right;" | 5.36 | | style="text-align:right;" | 5.36 | ||
| style="text-align:center;" |Sarurutrigu | |||
| style="text-align:center;" | Porwell | | style="text-align:center;" | Porwell | ||
| style="text-align:center;" | | | style="text-align:center;" | | ||
| Line 426: | Line 353: | ||
| |<nowiki> | 2 -2 2 0 -1 </nowiki>> | | |<nowiki> | 2 -2 2 0 -1 </nowiki>> | ||
| style="text-align:right;" | 17.40 | | style="text-align:right;" | 17.40 | ||
| style="text-align:center;" |Luyoyo | |||
| style="text-align:center;" | Ptolemisma | | style="text-align:center;" | Ptolemisma | ||
| style="text-align:center;" | | | style="text-align:center;" | | ||
| Line 433: | Line 361: | ||
| |<nowiki> | -3 2 -1 2 -1 </nowiki>> | | |<nowiki> | -3 2 -1 2 -1 </nowiki>> | ||
| style="text-align:right;" | 3.93 | | style="text-align:right;" | 3.93 | ||
| style="text-align:center;" |Luzozogu | |||
| style="text-align:center;" | Werckisma | | style="text-align:center;" | Werckisma | ||
| style="text-align:center;" | | | style="text-align:center;" | | ||
| Line 438: | Line 367: | ||
|} | |} | ||
=23 tone [[Equal_Modes|Equal Modes]]:= | =MOS Scales= | ||
The chart below shows some of the [[MOSScales|Moment of Symmetry (MOS)]] modes of [[Mavila|Mavila]] available in 23edo, mainly Pentatonic(5-note), anti-diatonic(7-note), 9- and 16-note MOSs. Here the outer ring represents individual step of 23edo itself, while the rings moving inward represent 16, 9, 7 and 5 note MOSs: | |||
[[File:23edoMavilaMOS.jpg|alt=23edoMavilaMOS.jpg|23edoMavilaMOS.jpg]] | |||
==23 tone [[Equal_Modes|Equal Modes]]:== | |||
{| class="wikitable" | {| class="wikitable" | ||
| Line 619: | Line 554: | ||
| | | | | | ||
|} | |} | ||
==Kosmorsky's Sephiroth modes== | |||
I would argue that the most significant modes of 23 edo are those of the 2 2 2 3 2 2 3 2 2 3 scale ([[3L_7s|3L 7s fair mosh]]); This is derived from extending the ~1/3 comma tempered 13th Harmonic, two of which add up to the 21st harmonic and three add up to the 17th harmonic almost perfectly. Interestingly, the chord 8:13:21:34 is a fragment of the fibonacci sequence. | |||
Notated in ascending (standard) form. I have named these 10 modes according to the Sephiroth as follows: | |||
2 2 2 3 2 2 3 2 2 3 - Mode Keter | |||
2 2 3 2 2 3 2 2 3 2 - Chesed | |||
2 3 2 2 3 2 2 3 2 2 - Netzach | |||
3 2 2 3 2 2 3 2 2 2 - Malkuth | |||
2 2 3 2 2 3 2 2 2 3 - Binah | |||
2 3 2 2 3 2 2 2 3 2 - Tiferet | |||
3 2 2 3 2 2 2 3 2 2 - Yesod | |||
2 2 3 2 2 2 3 2 2 3 - Chokmah | |||
2 3 2 2 2 3 2 2 3 2 - Gevurah | |||
3 2 2 2 3 2 2 3 2 2 - Hod | |||
=Books= | =Books= | ||
| Line 655: | Line 615: | ||
This movie is a series of still shots Chris took during the process of making a 23 edo guitar in a stick like form. At the end the guitar is played without effects etc. and the open string tuning is sounded - which starts with a normal E and then adjusted to the 9th / 7th fret unison, like a typical 12edo guitar fashion. | This movie is a series of still shots Chris took during the process of making a 23 edo guitar in a stick like form. At the end the guitar is played without effects etc. and the open string tuning is sounded - which starts with a normal E and then adjusted to the 9th / 7th fret unison, like a typical 12edo guitar fashion. | ||
<youtube> | =Music= | ||
[https://soundcloud.com/overtoneshock/curiosity-finds-a-frown-23-edo Curiosity Finds a Frown, by Stephen Weigel] | |||
[http://soonlabel.com/xenharmonic/archives/2460 Chromatic canon, by Claudi Meneghin] | |||
<span style=""><span style="">''[http://home.vicnet.net.au/%7Eepoetry/family.mp3 The Family Supper]''</span></span> by [[Warren_Burt|Warren Burt]] | |||
<span style=""><span style="">''[http://www.youtube.com/watch?v=Hqst8MaRiYM Icositriphonic Heptatonic MOS]''</span></span> by [[Igliashon_Jones|Igliashon Jones]] | |||
<span style=""><span style="">''[http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Igs/City%20Of%20The%20Asleep%20-%20His%20Wandering%20Kinship%20with%20Ashes.mp3 His Wandering Kinship with Ashes]''</span></span> by Igliashon Jones | |||
<span style=""><span style="">''[http://www.nonoctave.com/tunes/CosmicChamber.mp3 Cosmic Chamber]''</span></span> by [[X._J._Scott|X. J. Scott]] | |||
<span style=""><span style="">''[http://www.nonoctave.com/tunes/Daisies.mp3 Daisies on the Beach]''</span></span> by X. J. Scott | |||
<span style="background-position: 100% 50%; cursor: pointer; padding-right: 10px;"><span style=""><span style="">''[http://www.akjmusic.com/audio/boogie_pie.mp3 Boogie Pie]''</span></span></span>by [[Aaron_Krister_Johnson|Aaron Krister Johnson]] | |||
<span style=""><span style="">''[http://clones.soonlabel.com/public/micro/23edo/daily20110619_23edo_23_chilled.mp3 23 Chilled]''</span></span> by [[Chris_Vaisvil|Chris Vaisvil]] | |||
<span style=""><span style="">''[http://www.seraph.it/dep/det/DesertWinds.mp3 Desert Winds]''</span></span> by [[Carlo_Serafini|Carlo Serafini]] ([http://www.seraph.it/blog_files/926007c7483e4abc5a48d582c0667947-105.html blog entry]) | |||
<span style=""><span style="">''[http://www.seraph.it/dep/det/23Laments.mp3 23 Laments]''</span></span> by [[Carlo_Serafini|Carlo Serafini]] ([http://www.seraph.it/blog_files/b2bf6f252efd467ee36ecc332a4872ac-106.html blog entry]) | |||
<span style="">''[http://www.seraph.it/dep/det/Doomsday23.mp3 Doomsday 23]''</span> by [[Carlo_Serafini|Carlo Serafini]] ([http://www.seraph.it/blog_files/add481fdf4ae8c3afe56a0d2cb6dd672-164.html blog entry]) | |||
<span style="">''[http://www.seraph.it/dep/int/Adagio23ForStrings.mp3 Barber’s Adagio For Strings in 23ED2]''</span> by [[Carlo_Serafini|Carlo Serafini]] ([http://www.seraph.it/blog_files/9e630d3f8ba93ab8264a3862dac950ce-192.html blog entry]) | |||
<span style="">''[http://www.seraph.it/dep/det/Nubian%20Dance.mp3 Nubian Dance]''</span> by [[Carlo_Serafini|Carlo Serafini]] ([http://www.seraph.it/blog_files/694f0a26d29cd2a215f37754dd8428c3-237.html blog entry]) | |||
<span style="">''[http://www.seraph.it/dep/det/AroundTheBonfire.mp3 Around the bonfire]''</span> by [[Carlo_Serafini|Carlo Serafini]] ([http://www.seraph.it/blog_files/9c6c54c593bc4720c8bd775fd5e244f4-261.html blog entry]) | |||
''Allegro Moderato'' by Easley Blackwood | |||
[http://andrewheathwaite.bandcamp.com/track/pentaswing Pentaswing] [[Technical_Notes_for_Newbeams#Track notes:-Pentaswing|Notes]] by [[Andrew_Heathwaite|Andrew Heathwaite]] | |||
<span style="">''[http://micro.soonlabel.com/MOS/20120418-9mos-mindaugas.mp3 Mindaugas Rex Lithuaniae]''</span> by [http://chrisvaisvil.com/?p=2267 Chris Vaisvil] (in Superpelog-9 tuning) | |||
''[http://micro.soonlabel.com/23edo/Tutim_Dennsuul/T%fatim%20Dennsuul%20-%20Indigorange.mp3 Indigorange]'' by Tutim Dennsuul | |||
''[http://micro.soonlabel.com/23edo/Tutim_Dennsuul/T%fatim%20Dennsuul%20-%20Wignud.mp3 Wignud]'' by Tutim Dennsuul | |||
''[http://micro.soonlabel.com/23edo/Tutim_Dennsuul/Tutim%20Dennsuul%20-%20%20Harid.mp3 Harid]'' by Tutim Dennsuul | |||
''[https://soundcloud.com/nanovibrationalrelations/a-rest-in-the-desert-23edo A Rest In The Desert]'' [http://micro.soonlabel.com/gene_ward_smith/Others/Mcandrew/A%20Rest%20In%20The%20Desert%20(23edo).mp3 play] by Gary Mcandrew | |||
''[http://spectropolrecords.bandcamp.com/track/jacky-ligon-numenoctagon Numenoctagon]'' by Jacky Ligon (on spectropolrecords) | |||
[http://www.dubbhism.com/2014/02/out-now-ligon-sevish-dubshot-23.html#more 23 (album)] by Jacky Ligon, Sevish & Tony Dubshot ([https://soundcloud.com/ism-studio/sets/ligon-sevish-dubshot-23 soundcloud]) | |||
[https://soundcloud.com/shunya-kiyokawa/23edo-klavier8 23EDO Klavier8] by [[Shunya_Kiyokawa|Shunya Kiyokawa]]<youtube>K4iO7k152og</youtube> | |||
[[Category:11/7]] | [[Category:11/7]] | ||
[[Category:23-tone]] | [[Category:23-tone]] | ||
Revision as of 05:56, 14 December 2019
Theory
23-TET, or 23-EDO, is a tempered musical system which divides the octave into 23 equal parts of approximately 52.173913 cents, which is also called with the neologism Icositriphony (Icositrifonía). It has good approximations for 5/3, 11/7, 13 and 17, allowing it to represent the 2.5/3.11/7.13.17 just intonation subgroup. If to this subgroup is added the commas of 17-limit 46edo, the larger 17-limit 2*23 subgroup 2.9.15.21.33.13.17 is obtained. This is the largest subgroup on which 23 has the same tuning and commas as does 17-limit·46edo, and may be regarded as a basis for analyzing the harmony of 23-EDO so far, as approximations to just intervals goes. 23edo is the 9th prime edo, following 19edo and coming before 29edo.
23-EDO was proposed by ethnomusicologist Erich von Hornbostel as the result of continuing a circle of "blown" fifths of ~678-cent fifths that (he argued) resulted from "overblowing" a bamboo pipe.
23-EDO is also significant in that it is the largest EDO that fails to approximate the 3rd, 5th, 7th, and 11th harmonics within 20 cents, which makes it well-suited for musicians seeking to explore harmonic territory that is unusual even for the average microtonalist. Oddly, despite the fact that it fails to approximate these harmonics, it approximates the intervals between them (5/3, 7/3, 11/3, 7/5, 11/7, and 11/5) very well. The lowest harmonics well-approximated by 23-EDO are 13, 17, 21, and 23. See here for more details. Also note that some approximations can be improved by octave stretching.
As with 9-EDO, 16-EDO, and 25-EDO, one way to treat 23-EDO is as a Pelogic temperament, tempering out the "comma" of 135/128 and equating three 'acute 4/3's with 5/1 (related to the Armodue system). This means mapping '3/2' to 13 degrees of 23, and results in a 7 notes Anti-diatonic scale of 3 3 4 3 3 3 4 (in steps of 23-EDO), which extends to 9 notes Superdiatonic scale (3 3 3 1 3 3 3 3 1). One can notate 23-EDO using the Armodue system, but just like notating 17-EDO with familiar diatonic notation, flats will be lower in pitch than enharmonic sharps, because in 23-EDO, the "Armodue 6th" is sharper than it is in 16-EDO, just like the Diatonic 5th in 17-EDO is sharper than in 12-EDO. In other words, 2b is lower in pitch than 1#, just like how in 17-EDO, Eb is lower than D#.
However, one can also map 3/2 to 14 degrees of 23-EDO without significantly increasing the error, taking us to a 7-limit temperament where two 'broad 3/2's equals 7/3, meaning 28/27 is tempered out, and six 4/3's octave-reduced equals 5/4, meaning 4096/3645 is tempered out. Both of these are very large commas, so this is not at all an accurate temperament, but it is related to 13-EDO and 18-EDO and produces MOS scales of 5 and 8 notes: 5 5 4 5 4 (the "anti-pentatonic") and 4 1 4 1 4 4 1 4 (the "quarter-tone" version of the Blackwood/Rapoport/Wilson 13-EDO "subminor" scale). Alternatively we can treat this temperament as a 2.9.21 subgroup, and instead of calling 9 degrees of 23-EDO a Sub-"4/3", we can call it 21/16. Here three 21/16's gets us to 9/4, meaning 1029/1024 is tempered out. This allows us to treat a triad of 0-4-9 degrees of 23-EDO as an approximation to 16:18:21, and 0-5-9 as 1/(16:18:21); both of these triads are abundant in the 8-note MOS scale.
Notation
23edo can be notated with conventional notation, including the staff, note names, relative notation, etc. in two ways. The first preserves the melodic meaning of sharp/flat, major/minor and aug/dim, in that sharp is higher pitched than flat, and major/aug is wider than minor/dim. The disadvantage to this approach is that conventional interval arithmetic no longer works. e.g. M2 + M2 isn't M3, and D + M2 isn't E. Chord names are different because C - E - G isn't P1 - M3 - P5.
The second approach preserves the harmonic meaning of sharp/flat, major/minor and aug/dim, in that the former is always further fifthwards on the chain of fifths than the latter. Sharp is lower in pitch than flat, and major/aug is narrower than minor/dim. While this approach may seem bizarre at first, interval arithmetic and chord names work as usual. Furthermore, conventional 12edo music can be directly translated to 23edo "on the fly".
Armodue notation is a nonatonic notation that uses the numbers 1-9 as note names.
| Degree* | Cents | Approximate
Ratios ** |
Major wider
than minor |
Major narrower
than minor |
Armodue
Notation |
Notes | ||
| 0 | 0.000 | 1/1 | P1 | D | P1 | D | 1 | |
| 1 | 52.174 | 33/32, 34/33 | A1 | D# | d1 | Db | 2b | |
| 2 | 104.348 | 17/16, 16/15, 18/17 | d2 | Eb | A2 | E# | 1# | Less than 1 cent off 17/16 |
| 3 | 156.522 | 11/10, 12/11, 35/32 | m2 | E | M2 | E | 2 | |
| 4· | 208.696 | 9/8, 44/39 | M2 | E# | m2 | Eb | 3b | |
| 5 | 260.87 | 7/6, 15/13, 29/25 | A2, d3 | Ex, Fbb | d2, A3 | Ebb, Fx | 2# | |
| 6 | 313.0435 | 6/5 | m3 | Fb | M3 | F# | 3 | Much better 6/5 than 12-edo |
| 7· | 365.217 | 16/13, 21/17, 26/21 | M3 | F | m3 | F | 4b | |
| 8 | 417.391 | 14/11, 33/26 | A3 | F# | d3 | Fb | 3# | Practically just 14/11 |
| 9 | 469.565 | 21/16, 17/13 | d4 | Gb | A4 | G# | 4 | |
| 10· | 521.739 | 23/17, 88/65, 256/189 | P4 | G | P4 | G | 5 | |
| 11 | 573.913 | 7/5, 32/23, 46/33 | A4 | G# | d4 | Gb | 6b | |
| 12 | 626.087 | 10/7, 23/16, 33/23 | d5 | Ab | A5 | A# | 5# | |
| 13· | 678.261 | 34/23, 65/44, 189/128 | P5 | A | P5 | A | 6 | Great Hornbostel generator |
| 14 | 730.435 | 32/21, 26/17 | A5 | A# | d5 | Ab | 7b | |
| 15 | 782.609 | 11/7, 52/33 | d6 | Bb | A6 | B# | 6# | |
| 16· | 834.783 | 13/8, 34/21, 21/13 | m6 | B | M6 | B | 7 | |
| 17 | 886.9565 | 5/3 | M6 | B# | m6 | Bb | 8b | |
| 18 | 939.13 | 12/7, 26/15, 50/29 | A6, d7 | Bx, Cbb | d6, A7 | Bbb, Cx | 7# | |
| 19· | 991.304 | 16/9, 39/22 | m7 | Cb | M7 | C# | 8 | |
| 20 | 1043.478 | 11/6, 20/11, 64/35 | M7 | C | m7 | C | 9b | |
| 21 | 1095.652 | 15/8, 17/9, 32/17 | A7 | C# | d7 | Cb | 8# | |
| 22 | 1147.826 | 33/17, 64/33 | d8 | Db | A8 | D# | 9 | |
| 23·· | 1200 | 2/1 | P8 | D | P8 | D | 1 | |
- The dots indicate which frets on a 23-edo guitar would have dots.
- Based on treating 23-EDO as a 2.9.15.21.33.13.17 subgroup temperament; other approaches are possible.
Armodue Notation
Commas
23 EDO tempers out the following commas. (Note: This assumes the val < 23 36 53 65 80 85 |.) Also note the discussion above, where there are some commas mentioned that are not in the standard comma list (e.g., 28/27).
| Ratio | Monzo | Cents | Color Name | Name 1 | Name 2 | Name 3 |
|---|---|---|---|---|---|---|
| 135/128 | | -7 3 1 > | 92.18 | Layobi | Major Chroma | Major Limma | Pelogic Comma |
| 15625/15552 | | -6 -5 6 > | 8.11 | Tribiyo | Kleisma | Semicomma Majeur | |
| 36/35 | | 2 2 -1 -1 > | 48.77 | Rugu | Septimal Quarter Tone | ||
| 525/512 | | -9 1 2 1 > | 43.41 | Lazoyoyo | Avicennma | Avicenna's Enharmonic Diesis | |
| 4000/3969 | | 5 -4 3 -2 > | 13.47 | Rurutriyo | Octagar | ||
| 6144/6125 | | 11 1 -3 -2 > | 5.36 | Sarurutrigu | Porwell | ||
| 100/99 | | 2 -2 2 0 -1 > | 17.40 | Luyoyo | Ptolemisma | ||
| 441/440 | | -3 2 -1 2 -1 > | 3.93 | Luzozogu | Werckisma |
MOS Scales
The chart below shows some of the Moment of Symmetry (MOS) modes of Mavila available in 23edo, mainly Pentatonic(5-note), anti-diatonic(7-note), 9- and 16-note MOSs. Here the outer ring represents individual step of 23edo itself, while the rings moving inward represent 16, 9, 7 and 5 note MOSs:
23 tone Equal Modes:
| 10 10 3 | |
| 9 9 5 | |
| 8 8 7 | |
| 7 7 7 2 | |
| 7 2 7 7 | |
| 6 6 6 5 | |
| 6 5 6 6 | |
| 5 4 5 5 4 | 3L 2s (father) |
| 5 4 5 4 5 | |
| 7 1 7 7 1 | |
| 7 1 7 1 7 | |
| 5 5 5 5 3 | 4L 1s (bug) |
| 5 3 5 5 5 | |
| 4 4 4 4 4 3 | 5L 1s (Grumpy hexatonic) |
| 4 3 4 4 4 4 | |
| 5 1 5 1 5 1 5 | 4L 3s (mish) |
| 3 3 3 5 3 3 3 | 1L 6s (Happy heptatonic) |
| 4 3 3 3 3 3 4 | 2L 5s (mavila, anti-diatonic) |
| 3 4 3 3 4 3 3 | |
| 3 3 4 3 3 3 4 | |
| 3 3 3 4 3 3 4 | |
| 3 3 3 4 3 4 3 | |
| 2 5 2 5 2 5 2 | 3L 4s (mosh) |
| 4 1 4 4 1 4 4 1 | 5L 3s (unfair father) |
| 3 3 3 3 3 3 3 2 | 7L 1s (Grumpy octatonic) |
| 3 2 3 3 3 3 3 3 | |
| 3 3 3 1 3 3 3 3 1 | 7L 2s (mavila superdiatonic) |
| 3 3 1 3 3 3 1 3 3 | |
| 3 2 3 2 3 2 3 2 3 | 5L 4s (unfair bug) |
| 2 2 2 3 2 2 3 2 2 3 | Mode Keter |
| 2 2 3 2 2 3 2 2 3 2 | Chesed |
| 2 3 2 2 3 2 2 3 2 2 | Netzach |
| 3 2 2 3 2 2 3 2 2 2 | Malkuth |
| 2 2 3 2 2 3 2 2 2 3 | Binah |
| 2 3 2 2 3 2 2 2 3 2 | Tiferet |
| 3 2 2 3 2 2 2 3 2 2 | Yesod |
| 2 2 3 2 2 2 3 2 2 3 | Chokmah |
| 2 3 2 2 2 3 2 2 3 2 | Gevurah |
| 3 2 2 2 3 2 2 3 2 2 | Hod |
| 3 1 3 1 3 1 3 1 3 1 3 | Palestine 11 |
| 2 2 2 2 1 2 2 2 1 2 2 2 1 | Mode Tishrei |
| 2 2 2 1 2 2 2 1 2 2 2 1 2 | Cheshvan |
| 2 2 1 2 2 2 1 2 2 2 1 2 2 | Kislev |
| 2 1 2 2 2 1 2 2 2 1 2 2 2 | Tevet |
| 1 2 2 2 1 2 2 2 1 2 2 2 2 | Shvat |
| 2 2 2 1 2 2 2 1 2 2 2 2 1 | Adar minor |
| 2 2 1 2 2 2 1 2 2 2 2 1 2 | Adar major |
| 2 1 2 2 2 1 2 2 2 2 1 2 2 | Nisan |
| 1 2 2 2 1 2 2 2 2 1 2 2 2 | Iyar |
| 2 2 2 1 2 2 2 2 1 2 2 2 1 | Sivan |
| 2 2 1 2 2 2 2 1 2 2 2 1 2 | Tammuz |
| 2 1 2 2 2 2 1 2 2 2 1 2 2 | Av |
| 1 2 2 2 2 1 2 2 2 1 2 2 1 | Elul |
| 2 2 1 2 2 1 2 2 1 2 2 1 2 1 | |
| 2 1 2 2 1 2 2 1 2 2 1 2 2 1 | Palestine 14 |
| 1 1 1 4 1 1 1 1 4 1 1 1 1 4 | |
| 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 | |
| 2 1 1 2 1 1 2 1 1 2 1 1 2 1 1 2 1 | Palestine 17 |
| 2 1 1 1 1 2 1 1 1 1 2 1 1 1 1 2 1 1 1 |
Kosmorsky's Sephiroth modes
I would argue that the most significant modes of 23 edo are those of the 2 2 2 3 2 2 3 2 2 3 scale (3L 7s fair mosh); This is derived from extending the ~1/3 comma tempered 13th Harmonic, two of which add up to the 21st harmonic and three add up to the 17th harmonic almost perfectly. Interestingly, the chord 8:13:21:34 is a fragment of the fibonacci sequence.
Notated in ascending (standard) form. I have named these 10 modes according to the Sephiroth as follows:
2 2 2 3 2 2 3 2 2 3 - Mode Keter
2 2 3 2 2 3 2 2 3 2 - Chesed
2 3 2 2 3 2 2 3 2 2 - Netzach
3 2 2 3 2 2 3 2 2 2 - Malkuth
2 2 3 2 2 3 2 2 2 3 - Binah
2 3 2 2 3 2 2 2 3 2 - Tiferet
3 2 2 3 2 2 2 3 2 2 - Yesod
2 2 3 2 2 2 3 2 2 3 - Chokmah
2 3 2 2 2 3 2 2 3 2 - Gevurah
3 2 2 2 3 2 2 3 2 2 - Hod
Books
Instruments
23-EDD 8-string Guitar by Ron Sword.
23-EDD Bass by Osmiorisbendi.
23-EDD Baritar by Osmiorisbendi.
23-EDD 5-string Acoustic Guitar by Tútim Dennsuul Wafiil (RIP).
Illustrative 23-EDD Keyboard
Chris Vaisvil made a do it yourself 23 edo electric guitar out of less than $50 of material. Here he is playing it.
Here is a still shot of the completed instrument.
This movie is a series of still shots Chris took during the process of making a 23 edo guitar in a stick like form. At the end the guitar is played without effects etc. and the open string tuning is sounded - which starts with a normal E and then adjusted to the 9th / 7th fret unison, like a typical 12edo guitar fashion.
Music
Curiosity Finds a Frown, by Stephen Weigel
Chromatic canon, by Claudi Meneghin
The Family Supper by Warren Burt
Icositriphonic Heptatonic MOS by Igliashon Jones
His Wandering Kinship with Ashes by Igliashon Jones
Daisies on the Beach by X. J. Scott
Boogie Pieby Aaron Krister Johnson
Desert Winds by Carlo Serafini (blog entry)
23 Laments by Carlo Serafini (blog entry)
Doomsday 23 by Carlo Serafini (blog entry)
Barber’s Adagio For Strings in 23ED2 by Carlo Serafini (blog entry)
Nubian Dance by Carlo Serafini (blog entry)
Around the bonfire by Carlo Serafini (blog entry)
Allegro Moderato by Easley Blackwood
Pentaswing Notes by Andrew Heathwaite
Mindaugas Rex Lithuaniae by Chris Vaisvil (in Superpelog-9 tuning)
Indigorange by Tutim Dennsuul
Wignud by Tutim Dennsuul
Harid by Tutim Dennsuul
A Rest In The Desert play by Gary Mcandrew
Numenoctagon by Jacky Ligon (on spectropolrecords)
23 (album) by Jacky Ligon, Sevish & Tony Dubshot (soundcloud)
23EDO Klavier8 by Shunya Kiyokawa