15edt: Difference between revisions
added unque's 15edt piece |
m Cleanup |
||
| Line 1: | Line 1: | ||
{{Infobox ET}} | {{Infobox ET}} | ||
{{ED intro}} | |||
== | == Theory == | ||
15edt corresponds to 9.4639…[[edo]]. It has [[harmonic]]s [[5/1|5]] and [[13/1|13]] closely in tune, but does not do so well for [[7/1|7]] and [[11/1|11]], which are quite sharp. It [[tempering out|tempers out]] the mowgli comma, {{monzo| 0 22 -15 }} in the 5-limit, which is tempered out by [[19edo]] but has an [[optimal patent val]] of [[303edo]]. As a 3.5.13-[[subgroup]] system, it tempers out [[2197/2187]] and [[3159/3125]]. Using the patent val, it tempers out [[375/343]] and [[6561/6125]] in the 7-limit; [[81/77]], [[125/121]], and [[363/343]] in the 11-limit; [[65/63]], [[169/165]], [[585/539]], and [[1287/1225]] in the 13-limit; [[51/49]], [[121/119]], [[125/119]], [[189/187]], and [[195/187]] in the 17-limit (no-twos subgroup). 15edt is related to the 2.3.5.13-subgroup temperament 19 & 123, which has a mapping {{mapping| 1 0 0 0 | 0 15 22 35 }}, where the generator, an approximate 27/25, has a [[POTE tuning]] of 126.773, very close to 15edt. | |||
With the patent 4, it tempers out 36/35, 64/63, and 375/343 in the 3 | With the patent [[4/1|4]], it tempers out [[36/35]], [[64/63]], and 375/343 in the 4.3.5.7 subgroup; [[45/44]], [[80/77]], 81/77, and 363/343 in the 4.3.5.7.11 subgroup; [[52/49]], 65/63, [[65/64]], [[143/140]], and 169/165 in the 4.3.5.7.11.13 subgroup; 51/49, [[52/51]], [[85/84]], and 121/119 in the 4.3.5.7.11.13.17 subgroup (as well as [[19ed4]]). The [[k*N subgroups|2*15 subgroup]] of 15edt is 4.3.5.14.22.13.34, on which b15 tempers out the same commas as the patent val for [[30edt]]. | ||
== Harmonics == | === Harmonics === | ||
{{Harmonics in equal|15|3|1|prec=2}} | {{Harmonics in equal|15|3|1|prec=2}} | ||
{{Harmonics in equal|15|3|1|prec=2| | {{Harmonics in equal|15|3|1|prec=2|columns=12|start=12|collapsed=true|Approximation of harmonics in 15edt (continued)}} | ||
==Intervals== | == Intervals == | ||
{| class="wikitable center-1 center-2 center-3" | |||
{| class="wikitable" | |||
|- | |- | ||
! | ! # | ||
!Cents | ! Cents | ||
!Hekts | ! Hekts | ||
!Approximate | ! Approximate ratios | ||
![[Polaris]] nonatonic notation | ! [[Polaris]] nonatonic notation | ||
|- | |- | ||
| | | 0 | ||
| | | | 0.0 | ||
| 0.0 | |||
| [[1/1]] | |||
| H | |||
|- | |- | ||
| 1 | |||
| 126.8 | |||
|86. | | 86.7 | ||
| [[14/13]], [[15/14]], [[16/15]], 29/27 | |||
| Ib | |||
|- | |- | ||
| 2 | |||
| 253.6 | |||
|173. | | 173.3 | ||
| [[15/13]] | |||
| vH#, ^Ib | |||
|- | |- | ||
| 3 | |||
| 380.4 | |||
|260 | | 260.0 | ||
| | | [[5/4]] | ||
| H# | |||
|- | |- | ||
| 4 | |||
| 507.2 | |||
|346. | | 346.7 | ||
| [[4/3]] | |||
| I | |||
|- | |- | ||
| 5 | |||
| | | 634.0 | ||
|433. | | 433.3 | ||
| [[13/9]] | |||
| J | |||
|- | |- | ||
| 6 | |||
| 760.8 | |||
|520 | | 520.0 | ||
| | | [[14/9]] | ||
| K | |||
|- | |- | ||
| 7 | |||
| 887.6 | |||
|606. | | 606.7 | ||
| [[5/3]] | |||
| L | |||
|- | |- | ||
| 8 | |||
| 1014.4 | |||
|793. | | 793.3 | ||
| [[9/5]] | |||
| Mb | |||
|- | |- | ||
| 9 | |||
| 1141.2 | |||
|780 | | 780.0 | ||
| | | [[27/14]] | ||
| vL#, ^Mb | |||
|- | |- | ||
| 10 | |||
| | | 1268.0 | ||
|866. | | 866.7 | ||
| [[27/13]] | |||
| L# | |||
|- | |- | ||
| 11 | |||
| 1394.8 | |||
|953. | | 953.3 | ||
| [[9/4]] | |||
| M | |||
|- | |- | ||
| 12 | |||
| 1521.6 | |||
|1040 | | 1040.0 | ||
| [[12/5]] | |||
| N | |||
|- | |- | ||
| 13 | |||
| 1648.4 | |||
|1126. | | 1126.7 | ||
| [[13/5]] | |||
| O | |||
|- | |- | ||
| 14 | |||
| 1775.2 | |||
|1213. | | 1213.3 | ||
| [[14/5]] | |||
| P | | P | ||
|- | |- | ||
| 15 | |||
| | | 1902.0 | ||
|1300 | | 1300.0 | ||
| [[3/1]] | |||
| H | | H | ||
|} | |} | ||
15edt contains 4 intervals from [[5edt]] and 2 intervals from [[3edt]], meaning that it contains 6 redundant intervals and 8 new intervals. The new intervals introduced include good approximations to 15/14, 15/13, 4/3, 5/3 and their tritave inverses. This allows for new chord possibilities such as 1:3:4:5:9:12:13:14:15: | 15edt contains 4 intervals from [[5edt]] and 2 intervals from [[3edt]], meaning that it contains 6 redundant intervals and 8 new intervals. The new intervals introduced include good approximations to 15/14, 15/13, 4/3, 5/3 and their tritave inverses. This allows for new chord possibilities such as 1:3:4:5:9:12:13:14:15:16… | ||
15edt also contains a [[5L 5s (3/1-equivalent)| | 15edt also contains a [[5L 5s (3/1-equivalent)|5L 5s]] mos similar to Blackwood Decatonic, which I{{who}} call Ebony. This mos has a period of 1/5 of the tritave and the generator is a single step. The major scale is sLsLsLsLsL, and the minor scale is LsLsLsLsLs. | ||
15edt approximates the 5th and 13th harmonics (and 29th) very well. Taking these as consonances one obtains an 3L | 15edt approximates the 5th and 13th harmonics (and 29th) very well. Taking these as consonances one obtains an 3L 3s mos "augmented scale", in which three 13/9 intervals close to a tritave, and another three are set 5/3 away. | ||
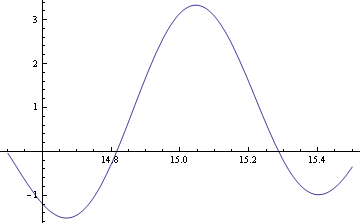
== JI approximation == | |||
=== Z function === | |||
Below is a plot of the [[The Riemann zeta function and tuning #Removing primes|no-twos Z function]] in the vicinity of 15edt: | |||
[[File:15edt.png|alt=15edt.png|15edt.png]] | |||
== Audio examples == | == Audio examples == | ||
| Line 127: | Line 134: | ||
A short composition by [[User:Unque|Unque]]. | A short composition by [[User:Unque|Unque]]. | ||
== | == Music == | ||
; [[nationalsolipsism]] | |||
* [https://www.youtube.com/watch?v=bC_Pc4jKm2k ''ox-idation''] (2012) | |||
[https://www.youtube.com/watch?v=bC_Pc4jKm2k | |||
[[Category:Macrotonal]] | [[Category:Macrotonal]] | ||
Revision as of 10:12, 10 February 2025
| ← 14edt | 15edt | 16edt → |
15 equal divisions of the tritave, perfect twelfth, or 3rd harmonic (abbreviated 15edt or 15ed3), is a nonoctave tuning system that divides the interval of 3/1 into 15 equal parts of about 127 ¢ each. Each step represents a frequency ratio of 31/15, or the 15th root of 3.
Theory
15edt corresponds to 9.4639…edo. It has harmonics 5 and 13 closely in tune, but does not do so well for 7 and 11, which are quite sharp. It tempers out the mowgli comma, [0 22 -15⟩ in the 5-limit, which is tempered out by 19edo but has an optimal patent val of 303edo. As a 3.5.13-subgroup system, it tempers out 2197/2187 and 3159/3125. Using the patent val, it tempers out 375/343 and 6561/6125 in the 7-limit; 81/77, 125/121, and 363/343 in the 11-limit; 65/63, 169/165, 585/539, and 1287/1225 in the 13-limit; 51/49, 121/119, 125/119, 189/187, and 195/187 in the 17-limit (no-twos subgroup). 15edt is related to the 2.3.5.13-subgroup temperament 19 & 123, which has a mapping [⟨1 0 0 0], ⟨0 15 22 35]], where the generator, an approximate 27/25, has a POTE tuning of 126.773, very close to 15edt.
With the patent 4, it tempers out 36/35, 64/63, and 375/343 in the 4.3.5.7 subgroup; 45/44, 80/77, 81/77, and 363/343 in the 4.3.5.7.11 subgroup; 52/49, 65/63, 65/64, 143/140, and 169/165 in the 4.3.5.7.11.13 subgroup; 51/49, 52/51, 85/84, and 121/119 in the 4.3.5.7.11.13.17 subgroup (as well as 19ed4). The 2*15 subgroup of 15edt is 4.3.5.14.22.13.34, on which b15 tempers out the same commas as the patent val for 30edt.
Harmonics
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -58.83 | +0.00 | +9.14 | +3.22 | -58.83 | +54.69 | -49.68 | +0.00 | -55.61 | +32.98 | +9.14 |
| Relative (%) | -46.4 | +0.0 | +7.2 | +2.5 | -46.4 | +43.1 | -39.2 | +0.0 | -43.9 | +26.0 | +7.2 | |
| Steps (reduced) |
9 (9) |
15 (0) |
19 (4) |
22 (7) |
24 (9) |
27 (12) |
28 (13) |
30 (0) |
31 (1) |
33 (3) |
34 (4) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -2.63 | -4.13 | +3.22 | +18.29 | +40.13 | -58.83 | -25.63 | +12.36 | +54.69 | -25.84 | +24.00 | -49.68 |
| Relative (%) | -2.1 | -3.3 | +2.5 | +14.4 | +31.6 | -46.4 | -20.2 | +9.8 | +43.1 | -20.4 | +18.9 | -39.2 | |
| Steps (reduced) |
35 (5) |
36 (6) |
37 (7) |
38 (8) |
39 (9) |
39 (9) |
40 (10) |
41 (11) |
42 (12) |
42 (12) |
43 (13) |
43 (13) | |
Intervals
| # | Cents | Hekts | Approximate ratios | Polaris nonatonic notation |
|---|---|---|---|---|
| 0 | 0.0 | 0.0 | 1/1 | H |
| 1 | 126.8 | 86.7 | 14/13, 15/14, 16/15, 29/27 | Ib |
| 2 | 253.6 | 173.3 | 15/13 | vH#, ^Ib |
| 3 | 380.4 | 260.0 | 5/4 | H# |
| 4 | 507.2 | 346.7 | 4/3 | I |
| 5 | 634.0 | 433.3 | 13/9 | J |
| 6 | 760.8 | 520.0 | 14/9 | K |
| 7 | 887.6 | 606.7 | 5/3 | L |
| 8 | 1014.4 | 793.3 | 9/5 | Mb |
| 9 | 1141.2 | 780.0 | 27/14 | vL#, ^Mb |
| 10 | 1268.0 | 866.7 | 27/13 | L# |
| 11 | 1394.8 | 953.3 | 9/4 | M |
| 12 | 1521.6 | 1040.0 | 12/5 | N |
| 13 | 1648.4 | 1126.7 | 13/5 | O |
| 14 | 1775.2 | 1213.3 | 14/5 | P |
| 15 | 1902.0 | 1300.0 | 3/1 | H |
15edt contains 4 intervals from 5edt and 2 intervals from 3edt, meaning that it contains 6 redundant intervals and 8 new intervals. The new intervals introduced include good approximations to 15/14, 15/13, 4/3, 5/3 and their tritave inverses. This allows for new chord possibilities such as 1:3:4:5:9:12:13:14:15:16…
15edt also contains a 5L 5s mos similar to Blackwood Decatonic, which I[who?] call Ebony. This mos has a period of 1/5 of the tritave and the generator is a single step. The major scale is sLsLsLsLsL, and the minor scale is LsLsLsLsLs.
15edt approximates the 5th and 13th harmonics (and 29th) very well. Taking these as consonances one obtains an 3L 3s mos "augmented scale", in which three 13/9 intervals close to a tritave, and another three are set 5/3 away.
JI approximation
Z function
Below is a plot of the no-twos Z function in the vicinity of 15edt:
Audio examples
A short composition by Unque.
Music
- ox-idation (2012)