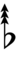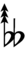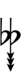77edo: Difference between revisions

With harmonic 3 less than a cent flat, harmonic 5 a bit over three cents sharp and 7 less flat than that, 77edo represents an excellent tuning choice for both valentine (hence also Carlos Alpha), the 31 & 46 temperament, and starling, the rank-3 temperament tempering out 126/125, giving the optimal patent val for 11-limit valentine and its 13-limit extension valentino, as well as 11-limit starling and oxpecker temperaments. It also gives the optimal patent val for grackle and various members of the unicorn family, with a generator of 4\77 instead of the 5\77 (which gives valentine). These are 7-limit alicorn and 11- and 13-limit camahueto.

77et tempers out the schisma (32805/32768) in the 5-limit; 126/125, 1029/1024, and 6144/6125 in the 7-limit; 121/120, 176/175, 385/384, and 441/440 in the 11-limit; and 196/195, 351/350, 352/351, 676/675 and 729/728 in the 13-limit.

The 17 and 19 are tuned fairly well, making it consistent to the no-11 21-odd-limit. The equal temperament tempers out 256/255 in the 17-limit; and 171/170, 361/360, 513/512, and 1216/1215 in the 19-limit.

Prime harmonics

Approximation of prime harmonics in 77edo
Harmonic		2	3	5	7	11	13	17	19	23
Error	Absolute (¢)	+0.00	-0.66	+3.30	-2.59	-5.86	+1.03	+4.14	-1.41	-4.90
Error	Relative (%)	+0.0	-4.2	+21.2	-16.6	-37.6	+6.6	+26.5	-9.0	-31.4
Steps (reduced)		77 (0)	122 (45)	179 (25)	216 (62)	266 (35)	285 (54)	315 (7)	327 (19)	348 (40)

Approximation of prime harmonics in 77edo (continued)
Harmonic		29	31	37	41	43	47	53	59	61
Error	Absolute (¢)	-1.01	-7.37	-1.99	+7.30	+2.77	+4.62	-0.78	+0.57	+5.19
Error	Relative (%)	-6.5	-47.3	-12.8	+46.8	+17.8	+29.7	-5.0	+3.6	+33.3
Steps (reduced)		374 (66)	381 (73)	401 (16)	413 (28)	418 (33)	428 (43)	441 (56)	453 (68)	457 (72)

Subsets and supersets

Since 77 factors into primes as 7 × 11, 77edo contains 7edo and 11edo as subset edos.

Intervals

#	Cents	Approximate ratios*	Ups and downs notation
0	0.0	1/1	D
1	15.6	81/80, 91/90, 99/98, 105/104	^D, ^^E♭♭
2	31.2	49/48, 55/54, 64/63, 65/64, 100/99	^^D, ^³E♭♭
3	46.8	33/32, 36/35, 40/39, 45/44, 50/49	^³D, v³E♭
4	62.3	26/25, 27/26, 28/27	v³D♯, vvE♭
5	77.9	21/20, 22/21, 25/24	vvD♯, vE♭
6	93.5	18/17, 19/18, 20/19	vD♯, E♭
7	109.1	16/15, 17/16	D♯, ^E♭
8	124.7	14/13, 15/14	^D♯, ^^E♭
9	140.3	13/12	^^D♯, ^³E♭
10	155.8	11/10, 12/11	^³D♯, v³E
11	171.4	21/19	v³D𝄪, vvE
12	187.0	10/9	vvD𝄪, vE
13	202.6	9/8	E
14	218.2	17/15	^E, ^^F♭
15	233.8	8/7	^^E, ^³F♭
16	249.4	15/13, 22/19	^³E, v³F
17	264.9	7/6	v³E♯, vvF
18	280.5	20/17	vvE♯, vF
19	296.1	13/11, 19/16, 32/27	F
20	311.7	6/5	^F, ^^G♭♭
21	327.3	98/81	^^F, ^³G♭♭
22	342.9	11/9, 17/14	^³F, v³G♭
23	358.4	16/13, 21/17	v³F♯, vvG♭
24	374.0	26/21, 56/45	vvF♯, vG♭
25	389.6	5/4	vF♯, G♭
26	405.2	19/15, 24/19, 33/26	F♯, ^G♭
27	420.8	14/11, 32/25	^F♯, ^^G♭
28	436.4	9/7	^^F♯, ^³G♭
29	451.9	13/10	^³F♯, v³G
30	467.5	17/13, 21/16	v³F𝄪, vvG
31	483.1	120/91	vvF𝄪, vG
32	498.7	4/3	G
33	514.3	27/20	^G, ^^A♭♭
34	529.9	19/14	^^G, ^³A♭♭
35	545.5	11/8, 15/11, 26/19	^³G, v³A♭
36	561.0	18/13	v³G♯, vvA♭
37	576.6	7/5	vvG♯, vA♭
38	592.2	24/17, 38/27, 45/32	vG♯, A♭
…	…	…

* As a 19-limit temperament

Notation

Sagittal notation

Evo flavor

Revo flavor

Ups and downs notation

Using Helmholtz–Ellis accidentals, 77edo can be notated using ups and downs notation:

Step offset	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Sharp symbol
Flat symbol

Approximation to JI

Zeta peak index

Tuning			Strength			Closest edo		Integer limit
ZPI	Steps per octave	Step size (cents)	Height	Integral	Gap	Edo	Octave (cents)	Consistent	Distinct
414zpi	76.9918536925042	15.5860645308353	8.194847	1.311364	17.029289	77edo	1200.12696887432	10	10

Regular temperament properties

Subgroup	Comma list	Mapping	Optimal 8ve stretch (¢)	Tuning error
Subgroup	Comma list	Mapping	Optimal 8ve stretch (¢)	Absolute (¢)	Relative (%)
2.3	[-122 77⟩	[⟨77 122]]	+0.207	0.207	1.33
2.3.5	32805/32768, 1594323/1562500	[⟨77 122 179]]	−0.336	0.785	5.04
2.3.5.7	126/125, 1029/1024, 10976/10935	[⟨77 122 179 216]]	−0.021	0.872	5.59
2.3.5.7.11	121/120, 126/125, 176/175, 10976/10935	[⟨77 122 179 216 266]]	+0.322	1.039	6.66
2.3.5.7.11.13	121/120, 126/125, 176/175, 196/195, 676/675	[⟨77 122 179 216 266 285]]	+0.222	0.974	6.25

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods per 8ve	Generator*	Cents*	Associated ratio*	Temperament
1	4\77	62.3	28/27	Unicorn / alicorn (77e) / camahueto (77) / qilin (77)
1	5\77	77.9	21/20	Valentine
1	9\77	140.3	13/12	Tsaharuk
1	15\77	233.8	8/7	Guiron
1	16\77	249.4	15/13	Hemischis (77e)
1	20\77	311.7	6/5	Oolong
1	23\77	358.4	16/13	Restles
1	31\77	483.1	45/34	Hemiseven
1	32\77	498.7	4/3	Grackle
1	34\77	529.9	512/375	Tuskaloosa / muscogee
1	36\77	561.0	18/13	Demivalentine
7	32\77 (1\77)	498.7 (15.6)	4/3 (81/80)	Absurdity
11	32\77 (3\77)	498.7 (46.8)	4/3 (36/35)	Hendecatonic

* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct

Music

Jake Freivald

A Seed Planted^{[dead link]}, in an organ version of Claudi Meneghin.

Joel Grant Taylor

Star 1-GrimaldiA+Bmod

Chris Vaisvil

77et Star

@@ Line 3: / Line 3: @@
 == Theory ==
-With [[3/1|harmonic 3]] less than a cent flat, [[5/1|harmonic 5]] a bit over three cents sharp and [[7/1|7]]'s less flat than that, 77edo represents an excellent tuning choice for both [[valentine]], the {{nowrap|31 &amp; 46}} temperament, and [[starling]], the [[126/125]] [[planar temperament]], giving the [[optimal patent val]] for [[11-limit]] valentine and its [[13-limit]] extensions dwynwen and valentino, as well as 11-limit starling and [[oxpecker]] temperaments. It also gives the optimal patent val for [[grackle]] and various members of the [[unicorn family]], with a [[generator]] of 4\77 instead of the 5\77 (which gives valentine). These are 7-limit [[Unicorn family #Alicorn|alicorn]] and 11- and 13-limit [[Unicorn family #Camahueto|camahueto]].
+With [[3/1|harmonic 3]] less than a cent flat, [[5/1|harmonic 5]] a bit over three cents sharp and [[7/1|7]] less flat than that, 77edo represents an excellent tuning choice for both [[valentine]] (hence also [[Carlos Alpha]]), the {{nowrap|31 & 46}} temperament, and [[starling]], the [[rank-3 temperament]] [[tempering out]] [[126/125]], giving the [[optimal patent val]] for [[11-limit]] valentine and its [[13-limit]] extension [[valentino]], as well as 11-limit starling and [[oxpecker]] temperaments. It also gives the optimal patent val for [[grackle]] and various members of the [[unicorn family]], with a [[generator]] of 4\77 instead of the 5\77 (which gives valentine). These are 7-limit [[unicorn family #Alicorn|alicorn]] and 11- and 13-limit [[unicorn family #Camahueto|camahueto]].
-et tempers out [[32805/32768]] in the [[5-limit]], [[126/125]], [[1029/1024]], and [[6144/6125]] in the 7-limit, [[121/120]], [[176/175]], [[385/384]], and [[441/440]] in the 11-limit, and [[196/195]], [[351/350]], [[352/351]], [[676/675]] and [[729/728]] in the 13-limit.
+et tempers out the [[schisma]] (32805/32768) in the [[5-limit]]; [[126/125]], [[1029/1024]], and [[6144/6125]] in the 7-limit; [[121/120]], [[176/175]], [[385/384]], and [[441/440]] in the 11-limit; and [[196/195]], [[351/350]], [[352/351]], [[676/675]] and [[729/728]] in the 13-limit.
 The [[17/1|17]] and [[19/1|19]] are tuned fairly well, making it [[consistent]] to the no-11 [[21-odd-limit]]. The equal temperament tempers out [[256/255]] in the 17-limit; and [[171/170]], [[361/360]], [[513/512]], and [[1216/1215]] in the 19-limit.
-edo is an excellent edo for [[Carlos Alpha]], since the difference between 5 steps of 77edo and 1 step of Carlos Alpha is only −0.042912 cents.
 === Prime harmonics ===
@@ Line 16: / Line 14: @@
 === Subsets and supersets ===
-Since 77 factors into primes as {{nowrap| 7 × 11 }}, 77edo contains [[7edo]] and [[11edo]] as subset edos.
+Since 77 factors into primes as {{nowrap|7 × 11}}, 77edo contains [[7edo]] and [[11edo]] as subset edos.
 == Intervals ==

77edo: Difference between revisions

Revision as of 11:19, 25 January 2025

Contents