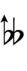62edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
Consolidate sections
→Instruments: Insert music section after this, starting with Bryan Deister's ''microtonal improvisation in 62edo'' (2025)
 
(18 intermediate revisions by 8 users not shown)
Line 1: Line 1:
{{Infobox ET}}
{{Infobox ET}}
{{EDO intro|62}}
{{ED intro}}


== Theory ==
== Theory ==
62edo's [[patent val]] of 62edo is a contorted [[31edo]] through the 11-limit, but it makes for a good tuning in the higher limits. In the 13-limit it tempers out [[169/168]], [[1188/1183]], [[847/845]] and [[676/675]]; in the 17-limit [[221/220]], [[273/272]], and [[289/288]]; in the 19-limit [[153/152]], [[171/170]], [[209/208]], [[286/285]], and [[361/360]]. Unlike 31edo, which has a sharp profile for primes [[13/1|13]], [[17/1|17]], [[19/1|19]] and [[23/1|23]], 62edo has a flat profile for these, as it removes the distinction of otonal and utonal [[superparticular]] pairs of the primes (e.g. 13/12 vs 14/13 for prime 13) by tempering out the corresponding [[square-particular]]s. This flat tendency extends to higher primes too, as the first prime harmonic that is tuned sharper than its [[5/4]] is its [[59/32]]. Interestingly, the relative size differences of consecutive harmonics are well preserved for all first 24 harmonics, and 62edo is one of the few meantone edos that achieve this, great for those who seek higher-limit [[meantone]] harmony.  
{{Nowrap| 62 {{=}} 2 × 31 }} and the [[patent val]] of 62edo is a [[contorsion|contorted]] [[31edo]] through the [[11-limit]], but it makes for a good tuning in the higher limits. In the 13-limit it [[tempering out|tempers out]] [[169/168]], [[1188/1183]], [[847/845]] and [[676/675]]; in the [[17-limit]] [[221/220]], [[273/272]], and [[289/288]]; in the [[19-limit]] [[153/152]], [[171/170]], [[209/208]], [[286/285]], and [[361/360]]. Unlike 31edo, which has a sharp profile for primes [[13/1|13]], [[17/1|17]], [[19/1|19]] and [[23/1|23]], 62edo has a flat profile for these, as it removes the distinction of otonal and utonal [[superparticular]] pairs of the primes (e.g. 13/12 vs 14/13 for prime 13) by tempering out the corresponding [[square-particular]]s. This flat tendency extends to higher primes too, as the first prime harmonic that is tuned sharper than its [[5/4]] is its [[59/32]]. Interestingly, the size differences between consecutive harmonics are monotonically decreasing for all first 24 harmonics, and 62edo is one of the few [[meantone]] edos that achieve this, great for those who seek higher-limit meantone harmony.  


It provides the [[optimal patent val]] for [[31st-octave temperaments#Gallium|gallium]], [[Starling temperaments #Valentine|semivalentine]] and [[Meantone family #Hemimeantone|hemimeantone]] temperaments.  
It provides the [[optimal patent val]] for [[gallium]], [[semivalentine]] and [[hemimeantone]] temperaments.  


Using the 35\62 generator, which leads to the {{val| 62 97 143 173 }} val, 62edo is also an excellent tuning for septimal [[mavila]] temperament; alternatively {{val| 62 97 143 172 }} [[support]]s [[hornbostel]].
Using the 35\62 generator, which leads to the {{val| 62 97 143 173 }} val, 62edo is also an excellent tuning for septimal [[mavila]] temperament; alternatively {{val| 62 97 143 172 }} [[support]]s [[hornbostel]].
Line 13: Line 13:


=== Subsets and supersets ===
=== Subsets and supersets ===
Since 62 factors into {{factorization|62}}, 62edo does not contain nontrivial subset edos other than [[2edo]] and 31edo. [[186edo]] and [[248edo]] are notable supersets.  
Since 62 factors into 2 × 31, 62edo does not contain nontrivial subset edos other than [[2edo]] and 31edo. [[186edo]] and [[248edo]] are notable supersets.  


=== Miscellaneous properties ===
=== Miscellany ===
62 years is the amount of years in a leap week calendar cycle which corresponds to a year of 365 days 5 hours 48 minutes 23 seconds, meaning it is both a simple cycle for a calendar, and 62 being a multiple of 31 makes it a harmonically useful and playable cycle. The corresponding maximal evenness scales are 15 & 62 and 11 & 62.  
62 years is the amount of years in a leap week calendar cycle which corresponds to a year of 365 days 5 hours 48 minutes 23 seconds, meaning it is both a simple cycle for a calendar, and 62 being a multiple of 31 makes it a harmonically useful and playable cycle. The corresponding maximal evenness scales are 15 & 62 and 11 & 62.  


The 11 & 62 temperament in the 2.9.7 subgroup tempers out 44957696/43046721, and the three generators of 17\62 correspond to [[16/9]]. It is possible to extend this to the 11-limit with comma basis {896/891, 1331/1296}, where 17\62 is mapped to [[11/9]] and two of them make [[16/11]]. In addition, three generators make the patent val 9/8, which is also created by combining the flat patent val fifth from 31edo with the sharp 37\62 fifth.
The 11 & 62 temperament is called mabon, named so because its associated year length corresponds to an autumnal equinoctial year. In the 2.9.7 subgroup tempers out 44957696/43046721, and the three generators of 17\62 correspond to [[16/9]]. It is possible to extend this to the 11-limit with comma basis {896/891, 1331/1296}, where 17\62 is mapped to [[11/9]] and two of them make [[16/11]]. In addition, three generators make the patent val 9/8, which is also created by combining the flat patent val fifth from 31edo with the sharp 37\62 fifth.


The 15 & 62 temperament, corresponding to the leap day cycle, is an unnamed extension to [[valentine]] in the 13-limit.
The 15 & 62 temperament, corresponding to the leap day cycle, is [[demivalentine]] in the 13-limit.


== Intervals ==
== Intervals ==
Line 349: Line 349:
== Notation ==
== Notation ==
=== Ups and downs notation ===
=== Ups and downs notation ===
62edo can be notated with quarter-tone accidentals and [[Alternative symbols for ups and downs notation #Sharp-4|ups and downs]]. This can be done by combining sharps and flats with arrows borrowed from extended [[Helmholtz–Ellis notation]]:
62edo can be notated with [[ups and downs]], spoken as up, dup, downsharp, sharp, upsharp etc. and down, dud, upflat etc. Note that dup is equivalent to dudsharp and dud is equivalent to dupflat.
 
{{Sharpness-sharp4a}}
[[Alternative symbols for ups and downs notation]] uses sharps and flats and quarter-tone accidentals combined with arrows, borrowed from extended [[Helmholtz–Ellis notation]]:
{{Sharpness-sharp4}}
{{Sharpness-sharp4}}
=== Sagittal notation ===
=== Sagittal notation ===
This notation uses the same sagittal sequence as EDOs [[69edo#Sagittal notation|69]] and [[76edo#Sagittal notation|76]], and is a superset of the notation for [[31edo#Sagittal notation|31-EDO]].
This notation uses the same sagittal sequence as EDOs [[69edo#Sagittal notation|69]] and [[76edo#Sagittal notation|76]], and is a superset of the notation for [[31edo#Sagittal notation|31-EDO]].
Line 789: Line 789:
== Approximation to JI ==
== Approximation to JI ==
=== Zeta peak index ===
=== Zeta peak index ===
{| class="wikitable center-all"
{{ZPI
|-
| zpi = 314
! colspan="3" | Tuning
| steps = 61.9380472360525
! colspan="3" | Strength
| step size = 19.3741981471691
! colspan="2" | Closest edo
| tempered height = 6.262952
! colspan="2" | Integer limit
| pure height = 4.11259
|-
| integral = 0.952068
! ZPI
| gap = 15.026453
! Steps per octave
| octave = 1201.20028512448
! Step size (cents)
| consistent = 8
! Height
| distinct = 8
! Integral
}}
! Gap
! Edo
! Octave (cents)
! Consistent
! Distinct
|-
| [[314zpi]]
| 61.9380472360525
| 19.3741981471691
| 6.262952
| 0.952068
| 15.026453
| 62edo
| 1201.20028512448
| 8
| 8
|}


== Regular temperament properties ==
== Regular temperament properties ==
Line 873: Line 856:
| 1
| 1
| 3\62
| 3\62
| 58.06
| 58.1
| 27/26
| 27/26
| [[Hemisecordite]]
| [[Hemisecordite]]
Line 879: Line 862:
| 1
| 1
| 7\62
| 7\62
| 135.48
| 135.5
| 13/12
| 13/12
| [[Doublethink]]
| [[Doublethink]]
Line 885: Line 868:
| 1
| 1
| 13\62
| 13\62
| 251.61
| 251.6
| 15/13
| 15/13
| [[Hemimeantone]]
| [[Hemimeantone]]
Line 891: Line 874:
| 1
| 1
| 17\62
| 17\62
| 329.03
| 329.0
| 16/11
| 16/11
| [[Mabon]]
| [[Mabon]]
|-
| 1
| 29\62
| 561.3
| 18/13
| [[Demivalentine]]
|-
|-
| 2
| 2
| 3\62
| 3\62
| 58.06
| 58.1
| 27/26
| 27/26
| [[Semihemisecordite]]
| [[Semihemisecordite]]
Line 903: Line 892:
| 2
| 2
| 4\62
| 4\62
| 77.42
| 77.4
| 21/20
| 21/20
| [[Semivalentine]]
| [[Semivalentine]]
Line 909: Line 898:
| 2
| 2
| 6\62
| 6\62
| 116.13
| 116.1
| 15/14
| 15/14
| [[Semimiracle]]
| [[Semimiracle]]
Line 915: Line 904:
| 2
| 2
| 26\62
| 26\62
| 503.22
| 503.2
| 4/3
| 4/3
| [[Semimeantone]]
| [[Semimeantone]]
Line 921: Line 910:
| 31
| 31
| 29\62<br>(1\62)
| 29\62<br>(1\62)
| 561.29<br>(19.35)
| 561.3<br>(19.4)
| 11/8<br>(196/195)
| 11/8<br>(196/195)
| [[Kumhar]] (62e)
| [[Kumhar]] (62e)
Line 927: Line 916:
| 31
| 31
| 19\62<br>(1\62)
| 19\62<br>(1\62)
| 367.74<br>(19.35)
| 367.7<br>(19.4)
| 16/13<br>(77/76)
| 16/13<br>(77/76)
| [[Gallium]]
| [[Gallium]]
|}
|}
<nowiki/>* [[Normal lists|Octave-reduced form]], reduced to the first half-octave, and [[Normal lists|minimal form]] in parentheses if distinct
<nowiki/>* [[Normal lists|Octave-reduced form]], reduced to the first half-octave, and [[Normal lists|minimal form]] in parentheses if distinct
== Instruments ==
=== Lumatone ===
* [[Lumatone mapping for 62edo]]
=== Skip fretting ===
'''[[Skip fretting]] system 62 6 11''' has strings tuned 11\62 apart, while frets are 6\62.
On a 4-string bass, here are your open strings:
0 11 22 33
A good supraminor 3rd is found on the 2nd string, 1st fret. A supermajor third is found on the open 3rd string. The major 6th can be found on the 4th string, 2nd fret.
5-string bass
51 0 11 22 33
This adds an interval of a major 7th (minus an 8ve) at the first string, 1st fret.
6-string guitar
0 11 22 33 44 55
”Major” 020131
7-string guitar
0 11 22 33 44 55 4
'''Skip fretting system 62 9 11''' is another 62edo skip fretting system. The 5th is on the 5th string. The major 3rd is on the 2nd string, 1st fret.
{{todo|add illustration|text=Base it off of the diagram from [[User:MisterShafXen/Skip fretting system 62 9 11]]}}
== Music ==
; [[Bryan Deister]]
* [https://www.youtube.com/shorts/UerD0NqBbng ''microtonal improvisation in 62edo''] (2025)

Latest revision as of 20:06, 22 July 2025

← 61edo 62edo 63edo →
Prime factorization 2 × 31
Step size 19.3548 ¢ 
Fifth 36\62 (696.774 ¢) (→ 18\31)
Semitones (A1:m2) 4:6 (77.42 ¢ : 116.1 ¢)
Consistency limit 7
Distinct consistency limit 7

62 equal divisions of the octave (abbreviated 62edo or 62ed2), also called 62-tone equal temperament (62tet) or 62 equal temperament (62et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 62 equal parts of about 19.4 ¢ each. Each step represents a frequency ratio of 21/62, or the 62nd root of 2.

Theory

62 = 2 × 31 and the patent val of 62edo is a contorted 31edo through the 11-limit, but it makes for a good tuning in the higher limits. In the 13-limit it tempers out 169/168, 1188/1183, 847/845 and 676/675; in the 17-limit 221/220, 273/272, and 289/288; in the 19-limit 153/152, 171/170, 209/208, 286/285, and 361/360. Unlike 31edo, which has a sharp profile for primes 13, 17, 19 and 23, 62edo has a flat profile for these, as it removes the distinction of otonal and utonal superparticular pairs of the primes (e.g. 13/12 vs 14/13 for prime 13) by tempering out the corresponding square-particulars. This flat tendency extends to higher primes too, as the first prime harmonic that is tuned sharper than its 5/4 is its 59/32. Interestingly, the size differences between consecutive harmonics are monotonically decreasing for all first 24 harmonics, and 62edo is one of the few meantone edos that achieve this, great for those who seek higher-limit meantone harmony.

It provides the optimal patent val for gallium, semivalentine and hemimeantone temperaments.

Using the 35\62 generator, which leads to the ⟨62 97 143 173] val, 62edo is also an excellent tuning for septimal mavila temperament; alternatively ⟨62 97 143 172] supports hornbostel.

Odd harmonics

Approximation of odd harmonics in 62edo
Harmonic 3 5 7 9 11 13 15 17 19 21 23
Error Absolute (¢) -5.18 +0.78 -1.08 +8.99 -9.38 -8.27 -4.40 -8.18 -7.19 -6.26 -8.92
Relative (%) -26.8 +4.0 -5.6 +46.5 -48.5 -42.7 -22.7 -42.3 -37.2 -32.4 -46.1
Steps
(reduced) 		98
(36) 		144
(20) 		174
(50) 		197
(11) 		214
(28) 		229
(43) 		242
(56) 		253
(5) 		263
(15) 		272
(24) 		280
(32)

Subsets and supersets

Since 62 factors into 2 × 31, 62edo does not contain nontrivial subset edos other than 2edo and 31edo. 186edo and 248edo are notable supersets.

Miscellany

62 years is the amount of years in a leap week calendar cycle which corresponds to a year of 365 days 5 hours 48 minutes 23 seconds, meaning it is both a simple cycle for a calendar, and 62 being a multiple of 31 makes it a harmonically useful and playable cycle. The corresponding maximal evenness scales are 15 & 62 and 11 & 62.

The 11 & 62 temperament is called mabon, named so because its associated year length corresponds to an autumnal equinoctial year. In the 2.9.7 subgroup tempers out 44957696/43046721, and the three generators of 17\62 correspond to 16/9. It is possible to extend this to the 11-limit with comma basis {896/891, 1331/1296}, where 17\62 is mapped to 11/9 and two of them make 16/11. In addition, three generators make the patent val 9/8, which is also created by combining the flat patent val fifth from 31edo with the sharp 37\62 fifth.

The 15 & 62 temperament, corresponding to the leap day cycle, is demivalentine in the 13-limit.

Intervals

Steps Cents Approximate ratios* Ups and downs notation
0 0.00 1/1 D
1 19.35 65/64, 66/65, 78/77, 91/90, 105/104 ^D, vE♭♭
2 38.71 33/32, 36/35, 45/44, 49/48, 50/49, 55/54, 56/55, 64/63 ^^D, E♭♭
3 58.06 26/25, 27/26 vD♯, ^E♭♭
4 77.42 21/20, 22/21, 23/22, 24/23, 25/24, 28/27 D♯, vvE♭
5 96.77 17/16, 18/17, 19/18, 20/19 ^D♯, vE♭
6 116.13 15/14, 16/15 ^^D♯, E♭
7 135.48 13/12, 14/13 vD𝄪, ^E♭
8 154.84 11/10, 12/11, 23/21 D𝄪, vvE
9 174.19 21/19 ^D𝄪, vE
10 193.55 9/8, 10/9, 19/17, 28/25 E
11 212.90 17/15 ^E, vF♭
12 232.26 8/7 ^^E, F♭
13 251.61 15/13, 22/19 vE♯, ^F♭
14 270.97 7/6 E♯, vvF
15 290.32 13/11, 19/16, 20/17 ^E♯, vF
16 309.68 6/5 F
17 329.03 17/14, 23/19 ^^F, G♭♭
18 348.39 11/9, 27/22, 28/23 ^^F, G♭♭
19 367.74 16/13, 21/17, 26/21 vF♯, ^G♭♭
20 387.10 5/4 F♯, vvG♭
21 406.45 19/15, 24/19 ^F♯, vG♭
22 425.81 9/7, 14/11, 23/18, 32/25 ^^F♯, G♭
23 445.16 13/10, 22/17 vF𝄪, ^G♭
24 464.52 17/13, 21/16, 30/23 F𝄪, vvG
25 483.87 25/19 ^F𝄪, vG
26 503.23 4/3 G
27 522.58 19/14, 23/17 ^G, vA♭♭
28 541.94 11/8, 15/11, 26/19 ^^G, A♭♭
29 561.29 18/13 vG♯, ^A♭♭
30 580.65 7/5, 25/18, 32/23 G♯, vvA♭
31 600.00 17/12, 24/17 E
32 619.35 10/7, 23/16, 36/25 ^^G♯, A♭
33 638.71 13/9 vG𝄪, ^A♭
34 658.06 16/11, 19/13, 22/15 G𝄪, vvA
35 677.42 28/19, 34/23 ^G𝄪, vA
36 696.77 3/2 A
37 716.13 38/25 ^A, vB♭♭
38 735.48 23/15, 26/17, 32/21 ^^A, B♭♭
39 754.84 17/11, 20/13 vA♯, ^B♭♭
40 774.19 11/7, 14/9, 25/16, 36/23 A♯, vvB♭
41 793.55 19/12, 30/19 ^A♯, vB♭
42 812.90 8/5 ^^A♯, B♭
43 832.26 13/8, 21/13, 34/21 vA𝄪, ^B♭
44 851.61 18/11, 23/14, 44/27 A𝄪, vvB
45 870.97 28/17, 38/23 ^A𝄪, vB
46 890.32 5/3 B
47 909.68 17/10, 22/13, 32/19 ^B, vC♭
48 929.03 12/7 ^^B, C♭
49 948.39 19/11, 26/15 vB♯, ^C♭
50 967.74 7/4 B♯, vvC
51 987.10 30/17 ^B♯, vC
52 1006.45 9/5, 16/9, 25/14, 34/19 C
53 1025.81 38/21 ^C, vD♭♭
54 1045.16 11/6, 20/11, 42/23 ^^C, D♭♭
55 1064.52 13/7, 24/13 vC♯, ^D♭♭
56 1083.87 15/8, 28/15 C♯, vvD♭
57 1103.23 17/9, 19/10, 32/17, 36/19 ^C♯, vD♭
58 1122.58 21/11, 23/12, 27/14, 40/21, 44/23, 48/25 ^^C♯, D♭
59 1141.94 25/13, 52/27 vC𝄪, ^D♭
60 1161.29 35/18, 49/25, 55/28, 63/32, 64/33, 88/45, 96/49, 108/55 C𝄪, vvD
61 1180.65 65/33, 77/39, 128/65, 180/91, 208/105 ^C𝄪, vD
62 1200.00 2/1 D

* 23-limit patent val, inconsistent intervals in italic

Notation

Ups and downs notation

62edo can be notated with ups and downs, spoken as up, dup, downsharp, sharp, upsharp etc. and down, dud, upflat etc. Note that dup is equivalent to dudsharp and dud is equivalent to dupflat.

Step offset 0 1 2 3 4 5 6 7 8 9
Sharp symbol               
Flat symbol
                

Alternative symbols for ups and downs notation uses sharps and flats and quarter-tone accidentals combined with arrows, borrowed from extended Helmholtz–Ellis notation:

Step offset 0 1 2 3 4 5 6 7 8 9
Sharp symbol
 
 		 
 		 
 		 
 		 
 		 
 		 
 		 
Flat symbol  
 		 
 
 
 
 		 

Sagittal notation

This notation uses the same sagittal sequence as EDOs 69 and 76, and is a superset of the notation for 31-EDO.

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation1053/102433/32

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation1053/102433/32

Evo-SZ flavor

Sagittal notationPeriodic table of EDOs with sagittal notation1053/102433/32

In the diagrams above, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's primary comma (the comma it exactly represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it approximately represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this EDO.

Armodue notation

Armodue nomenclature 8;3 relation
  • Ɨ = Thick (1/8-tone up)
  • ‡ = Semisharp (1/4-tone up)
  • b = Flat (5/8-tone down)
  • ◊ = Node (sharp/flat blindspot 1/2-tone)
  • # = Sharp (5/8-tone up)
  • v = Semiflat (1/4-tone down)
  • ⌐ = Thin (1/8-tone down)
# Cents Armodue notation Associated ratio
0 0.0 1
1 19.4 1Ɨ
2 38.7 1‡ (9#)
3 58.1 2b
4 77.4 1◊2
5 96.8 1#
6 116.1 2v
7 135.5 2⌐
8 154.8 2 11/10~12/11
9 174.2 2Ɨ
10 193.5 2‡
11 212.9 3b 8/7
12 232.3 2◊3
13 251.6 2#
14 271.0 3v
15 290.3 3⌐
16 309.7 3 6/5~7/6
17 329.0 3Ɨ
18 348.4 3‡
19 · 367.7 4b 5/4
20 387.1 3◊4
21 406.5 3#
22 425.8 4v (5b)
23 445.2 4⌐
24 464.5 4
25 483.9 4Ɨ (5v)
26 503.2 5⌐ (4‡)
27 · 522.6 5 4/3~11/8
28 541.9 5Ɨ
29 561.3 5‡ (4#)
30 580.6 6b 10/7
31 600.0 5◊6
32 619.4 5# 7/5
33 638.7 6v
34 658.1 6⌐
35 · 677.4 6 3/2~16/11
36 696.8 6Ɨ
37 716.1 6‡
38 735.5 7b
39 754.8 6◊7
40 774.2 6#
41 793.5 7v
42 812.9 7⌐
43 · 832.3 7 8/5
44 851.6 7Ɨ
45 871.0 7‡
46 890.3 8b 5/3~12/7
47 909.7 7◊8
48 929.0 7#
49 948.4 8v
50 967.7 8⌐
51 987.1 8 7/4
52 1006.5 8Ɨ
53 1025.8 8‡
54 1045.2 9b 11/6~20/11
55 1064.5 8◊9
56 1083.9 8#
57 1103.2 9v (1b)
58 1122.6 9⌐
59 1141.9 9
60 1161.3 9Ɨ (1v)
61 1180.6 1⌐ (9‡)
62 1200.0 1

Approximation to JI

Zeta peak index

Tuning Strength Octave (cents) Integer limit
ZPI Steps
per 8ve 		Step size
(cents) 		Height Integral Gap Size Stretch Consistent Distinct
Tempered Pure
314zpi 61.938047 19.374198 6.262952 4.11259 0.952068 15.026453 1201.200285 1.200285 8 8

Regular temperament properties

62edo is contorted 31edo through the 11-limit.

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3.5.7.11.13 81/80, 99/98, 121/120, 126/125, 169/168 [⟨62 98 144 174 214 229]] +1.38 1.41 7.28
2.3.5.7.11.13.17 81/80, 99/98, 121/120, 126/125, 169/168, 221/220 [⟨62 98 144 174 214 229 253]] +1.47 1.32 6.83
2.3.5.7.11.13.17.19 81/80, 99/98, 121/120, 126/125, 153/152, 169/168, 209/208 [⟨62 98 144 174 214 229 253 263]] +1.50 1.24 6.40
2.3.5.7.11.13.17.19.23 81/80, 99/98, 121/120, 126/125, 153/152, 161/160, 169/168, 209/208 [⟨62 98 144 174 214 229 253 263 280]] +1.55 1.18 6.09

Rank-2 temperaments

Table of rank-2 temperaments by generator
Periods
per 8ve 		Generator* Cents* Associated
ratio* 		Temperament
1 3\62 58.1 27/26 Hemisecordite
1 7\62 135.5 13/12 Doublethink
1 13\62 251.6 15/13 Hemimeantone
1 17\62 329.0 16/11 Mabon
1 29\62 561.3 18/13 Demivalentine
2 3\62 58.1 27/26 Semihemisecordite
2 4\62 77.4 21/20 Semivalentine
2 6\62 116.1 15/14 Semimiracle
2 26\62 503.2 4/3 Semimeantone
31 29\62
(1\62) 		561.3
(19.4) 		11/8
(196/195) 		Kumhar (62e)
31 19\62
(1\62) 		367.7
(19.4) 		16/13
(77/76) 		Gallium

* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct

Instruments

Lumatone

Skip fretting

Skip fretting system 62 6 11 has strings tuned 11\62 apart, while frets are 6\62.

On a 4-string bass, here are your open strings:

0 11 22 33

A good supraminor 3rd is found on the 2nd string, 1st fret. A supermajor third is found on the open 3rd string. The major 6th can be found on the 4th string, 2nd fret.

5-string bass

51 0 11 22 33

This adds an interval of a major 7th (minus an 8ve) at the first string, 1st fret.

6-string guitar

0 11 22 33 44 55

”Major” 020131

7-string guitar

0 11 22 33 44 55 4


Skip fretting system 62 9 11 is another 62edo skip fretting system. The 5th is on the 5th string. The major 3rd is on the 2nd string, 1st fret.

Music

Bryan Deister
Retrieved from "https://en.xen.wiki/index.php?title=62edo&oldid=205025"