8edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
CompactStar (talk | contribs)
5,020 edits
If you look at 11 or 13-limit subgroup temperaments, there are way, WAY better interpretations of it than father.
BudjarnLambeth (talk | contribs)
autopatrolled, emailconfirmed
18,215 edits
→Octave shrinking: Temporary improvement until the new standard is rolled out
 
(41 intermediate revisions by 16 users not shown)
Line 6: Line 6:
}}
}}
{{Infobox ET}}
{{Infobox ET}}
 
{{ED intro}}
'''8 equal divisions of the octave''' ('''8edo''') is the [[tuning system]] derived by dividing the [[octave]] into 8 equal steps of 150 [[cent]]s each, or the eighth root of 2.
 
== Theory ==
== Theory ==
{{Harmonics in equal|8|intervals=odd}}
[[File:8edo scale.mp3|thumb|A chromatic 8edo scale on C.]]
[[File:8edo scale.mp3|thumb|A chromatic 8edo scale on C.]]
=== Approximation to JI ===
8edo forms an odd and even pitch set of two diminished seventh chords, which when used in combination yield dissonance. The system has been described as a "barbaric" harmonic system, containing no good approximation of harmonics 3, 5, 7, 11, 13, and 17; even so, it does a good job representing the [[just intonation subgroup]]s 2.11/3.13/5, with good intervals of [[13/10]] and an excellent version of [[11/6]]. Stacking the 450-cent interval can result in some semi-consonant chords such as 0-3-6 degrees, although these still are quite dissonant compared to standard root-3rd-P5 triads, which are unavailable in 8edo.
8edo forms an odd and even pitch set of two diminished seventh chords, which when used in combination yield dissonance. The system has been described as a "barbaric" harmonic system, containing no good approximation of harmonics 3, 5, 7, 11, 13, and 17; even so, it does a good job representing the [[just intonation subgroup]]s 2.11/3.13/5, with good intervals of [[13/10]] and an excellent version of [[11/6]]. Stacking the 450-cent interval can result in some semi-consonant chords such as 0-3-6 degrees, although these still are quite dissonant compared to standard root-3rd-P5 triads, which are unavailable in 8edo.


Another way of looking at 8edo is to treat a chord of 0-1-2-3-4 degrees (0-150-300-450-600 cents) as approximating harmonics 10:11:12:13:14 (~0-165-316-454-583 cents), which is not too implausible if you can buy that 12edo is a 5-limit temperament. This interpretation would imply that 121/120, 144/143, 169/168, and hence also 36/35 and 66/65, are tempered out.
Another way of looking at 8edo is to treat a chord of 0-1-2-3-4 degrees (0-150-300-450-600 cents) as approximating harmonics 10:11:12:13:14 (~0-165-316-454-583 cents), which is not too implausible if you can buy that 12edo is a 5-limit temperament. This interpretation would imply that 121/120, 144/143, 169/168, and hence also 36/35 and 66/65, are tempered out.
=== Relationship with the father comma ===
When 8edo is treated as a very inaccurate 5-limit system, it ends up tempering out the [[Father]] comma, [[16/15]]. In fact, it is the largest edo that tempers this comma. What this means is that intervals 16/15 apart in 8edo map to the same note, such as [[4/3]] being mapped to the same note as [[5/4]].
Some other odd equivalencies include:
'''0-2-5''': which can be seen as a minor triad (10:12:15), a sus2 triad (9:8:12), or a major triad in first inversion (5:6:8).
'''0-3-5''': which can be seen as a major triad (4:5:6), a sus4 triad (6:8:9), or a minor chord in second inversion (15:20:24).
=== Odd harmonics ===
{{Harmonics in equal|8|intervals=odd}}
=== Octave shrinking ===
8edo's approximation of [[JI]] can be improved via [[octave shrinking]]. Compressing 8edo's octave from 1200 [[cent]]s down to 1187 cents gives the tuning called [[29ed12]].
Of all prime [[harmonic]]s up to 31, pure-octave 8edo only manages to approximate 2/1 and 19/1 within 15 [[cents]], completely missing all the others.
By contrast, 29ed12 approximates 2/1, 11/1, 13/1, 17/1 and 31/1 all within 15 cents.
Of all integer harmonics up to 30, pure-octave 8edo approximates the following within 20 cents:
* 2, 4, 8, 16, 19, 27.
Of all integer harmonics up to 30, 29ed12 approximates the following within 20 cents:
* 2, 6, 11, 12, 13, 17, 20, 22, 25, 26.
This provides 29ed12 with a comparatively larger, more diverse palette of [[consonance]]s than pure-octaves 8edo.
The nearest [[zeta peak index]] tunings to 8edo don't have an interval within 20 cents of [[2/1]], making them unrecognisable as stretched or compressed 8edo but instead more like entirely new scales in their own right.
=== Subsets and supersets ===
8edo contains [[2edo]] and [[4edo]] as subsets. Among its supersets are [[16edo]], [[24edo]], [[32edo]], ….
== Intervals ==
{| class="wikitable"
|-
! rowspan="2" | Steps
! rowspan="2" | Cents
! colspan="3" | JI approximation
!Other
|-
! 2.11/3.13/5.19*
! 2.5/3.11/3.13/5*
! 10:11:12:13:14*
!Patent val ⟨8 13 19]
|-
| 0
| 0
| 1/1
| 1/1
| 1/1
|1/1, 16/15
|-
| 1
| 150
| 12/11
| 12/11
| 12/11, 11/10
|10/9, 25/24
|-
| 2
| 300
| 19/16
| 6/5
| 6/5
|6/5, 9/8
|-
| 3
| 450
| 13/10
| 13/10
| 13/10
|4/3, 5/4
|-
| 4
| 600
|
|
| 7/5, 10/7
|27/20, 25/18, 36/25
|-
| 5
| 750
| 20/13
| 20/13
| 20/13
|3/2, 8/5
|-
| 6
| 900
| 32/19
| 5/3
| 5/3
|5/3, 16/9
|-
| 7
| 1050
| 11/6
| 11/6
| 20/11, 11/6
|9/5, 48/50
|-
| 8
| 1200
| 2/1
| 2/1
| 2/1
|2/1, 15/8
|}
<nowiki />* Allows [[inversion]] by 2/1; other interpretations also possible


== Notation ==
== Notation ==
8edo can be notated as a subset of 24edo, using [[Ups and Downs Notation|ups and downs]]. It can also be notated as a subset of 16edo, but this is a less intuitive notation.
=== Ups and downs notation ===
8edo can be notated as a subset of 24edo, using [[Ups and downs notation|ups and downs]]. It can also be notated as a subset of 16edo, but this is a less intuitive notation.


{| class="wikitable center-all"
{| class="wikitable center-all"
Line 23: Line 133:
! Edostep
! Edostep
! [[Cent]]s
! [[Cent]]s
! [[7mu]]s ([[Wikipedia: hexadecimal |hex]])
! colspan="2" | 24edo subset notation<br />([[Enharmonic unisons in ups and downs notation|EUs:]] vvA1 and d2)
! colspan="2" | 24edo subset notation
! colspan="2" | 16edo subset notation<br />(major narrower than minor)
! colspan="2" | 16edo subset notation<br>(major narrower than minor)
! colspan="2" | 16edo subset notation<br />(major wider than minor)
! colspan="2" | 16edo subset notation<br>(major wider than minor)
! [[3L&nbsp;2s]] notation<br />({{nowrap|J {{=}} 1/1}})
! [[3L 2s]] notation (J = 1/1)
! Audio
!Audio
|-
|-
| 0
| 0
| 0¢
| 0¢
| 0
| P1
| P1
| D
| D
Line 40: Line 148:
| D
| D
| J
| J
|[[File:0-0 unison.mp3|frameless]]
| [[File:0-0 unison.mp3|frameless]]
|-
|-
| 1
| 1
| 150
| 150
| 192 (C0)
| ~2
| ~2
| vE
| vE
Line 52: Line 159:
| E
| E
| K
| K
|[[File:0-150 (8-EDO).mp3|frameless]]
| [[File:0-150 (8-EDO).mp3|frameless]]
|-
|-
| 2
| 2
| 300
| 300
| 384 (180)
| m3
| m3
| F
| F
Line 64: Line 170:
| Fb
| Fb
| K#, Lb
| K#, Lb
|[[File:0-300 (12-EDO).mp3|frameless]]
| [[File:0-300 (12-EDO).mp3|frameless]]
|-
|-
| 3
| 3
| 450
| 450
| 576 (240)
| ^M3 / v4
| ^M3 / v4
| ^F# / vG
| ^F# / vG
Line 76: Line 181:
| F#, Gb
| F#, Gb
| L
| L
|[[File:0-450 (8-EDO).mp3|frameless]]
| [[File:0-450 (8-EDO).mp3|frameless]]
|-
|-
| 4
| 4
| 600
| 600
| 768 (300)
| A4, d5
| A4, d5
| G#, Ab
| G#, Ab
Line 88: Line 192:
| G#, Ab
| G#, Ab
| M
| M
|[[File:0-600 (12-EDO).mp3|frameless]]
| [[File:0-600 (12-EDO).mp3|frameless]]
|-
|-
| 5
| 5
| 750
| 750
| 960 (3C0)
| ^5, vm6
| ^5, vm6
| ^A, vBb
| ^A, vBb
Line 100: Line 203:
| A#, Bb
| A#, Bb
| M#, Nb
| M#, Nb
|[[File:0-750 (8-EDO).mp3|frameless]]
| [[File:0-750 (8-EDO).mp3|frameless]]
|-
|-
| 6
| 6
| 900
| 900
| 1152 (480)
| M6
| M6
| B
| B
Line 112: Line 214:
| B#
| B#
| N
| N
|[[File:0-900 (12-EDO).mp3|frameless]]
| [[File:0-900 (12-EDO).mp3|frameless]]
|-
|-
| 7
| 7
| 1050
| 1050
| 1344 (540)
| ~7
| ~7
| ^C
| ^C
Line 124: Line 225:
| C
| C
| N#, Jb
| N#, Jb
|[[File:0-1050 (8-EDO).mp3|frameless]]
| [[File:0-1050 (8-EDO).mp3|frameless]]
|-
|-
| 8
| 8
| 1200
| 1200
| 1536 (600)
| P8
| P8
| D
| D
Line 136: Line 236:
| D
| D
| J
| J
|[[File:0-1200 octave.mp3|frameless]]
| [[File:0-1200 octave.mp3|frameless]]
|}
|}


Line 145: Line 245:
D - D#/Eb - E - G - G#/Ab - A - C - C#/Db - D
D - D#/Eb - E - G - G#/Ab - A - C - C#/Db - D


P1 - A1/ms3 - Ms3 - P4d - A4d/d5d - P5d - ms7 - Ms7/d8d - P8d  (s = sub-, d = -oid)
P1 - A1/ms3 - Ms3 - P4d - A4d/d5d - P5d - ms7 - Ms7/d8d - P8d  (s = sub-, d = -oid, see [[5edo#Alternative notations|5edo]] notation)


pentatonic genchain of 5ths: ...Cb - Gb - Db - Ab - Eb - C - G - D - A - E - C# - G# - D# - A# - E#...
pentatonic genchain of 5ths: ...Cb - Gb - Db - Ab - Eb - C - G - D - A - E - C# - G# - D# - A# - E#...


pentatonic genchain of 5ths: ...d8d - d5d - ms3 - ms7 - P4d - P1 - P5d - Ms3 - Ms7 - A4d - A1... (s = sub-, d = -oid)
pentatonic genchain of 5ths: ...d8d - d5d - ms3 - ms7 - P4d - P1 - P5d - Ms3 - Ms7 - A4d - A1... (s = sub-, d = -oid)
[[Enharmonic unison]]: ds3


'''<u>Octatonic:</u>''' '''A B C D E F G H A'''  (every interval is a generator)
'''<u>Octatonic:</u>''' '''A B C D E F G H A'''  (every interval is a generator)


P1 - P2 - P3 - P4 - P5 - P6 - P7 - P8 - P9
P1 - P2 - P3 - P4 - P5 - P6 - P7 - P8 - P9
Enharmonic unison: none


'''<u>Heptatonic 2nd-generated</u>: D E F G * A B C D'''  (generator = 1\8 = perfect 2nd = 150¢)
'''<u>Heptatonic 2nd-generated</u>: D E F G * A B C D'''  (generator = 1\8 = perfect 2nd = 150¢)
Line 165: Line 269:
genchain of 2nds: ...A1 - A2 - M3 - M4 - M5 - M6 - P7 - P1 - P2 - m3 - m4 - m5 - m6 - d7 - d8...
genchain of 2nds: ...A1 - A2 - M3 - M4 - M5 - M6 - P7 - P1 - P2 - m3 - m4 - m5 - m6 - d7 - d8...


=== Chord names ===
Enharmonic unison: d2
[[Ups and Downs Notation #Chords and Chord Progressions|Ups and downs]] can name any 8edo chord. Alterations are always enclosed in parentheses, additions never are. An up, down or mid immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13).


8edo chords are very ambiguous, with many chord homonyms. Even the major and minor triads are homonyms. Chord components usually default to M2, M3, P4, P5, M6, m7, M9, P11 and M13. Thus D7 has a M3, P5 and m7. 8-edo chord names using 24edo subset names are greatly simplified by using different defaults: ~2, ^M3, v4, ^5, M6, ~7, ~9, v11 and M13. Thus D7 becomes ^M3, ^5 and ~7.
===Sagittal notation===
This notation is a subset of the notations for EDOs [[24edo#Sagittal notation|24]], [[48edo#Sagittal notation|48]], and [[72edo#Sagittal notation|72]].
====Evo flavor====
 
<imagemap>
File:8-EDO_Evo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 392 0 552 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 392 106 [[24-EDO#Sagittal_notation | 24-EDO notation]]
default [[File:8-EDO_Evo_Sagittal.svg]]
</imagemap>
 
====Revo flavor====
 
<imagemap>
File:8-EDO_Revo_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 400 0 560 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 400 106 [[24-EDO#Sagittal_notation | 24-EDO notation]]
default [[File:8-EDO_Revo_Sagittal.svg]]
</imagemap>
 
====Evo-SZ flavor====
 
<imagemap>
File:8-EDO_Evo-SZ_Sagittal.svg
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 376 0 536 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 376 106 [[24-EDO#Sagittal_notation | 24-EDO notation]]
default [[File:8-EDO_Evo-SZ_Sagittal.svg]]
</imagemap>
 
Because it contains no Sagittal symbols, this Evo-SZ Sagittal notation is also a Stein-Zimmerman notation.
 
== Chord names ==
[[Ups and downs notation #Chords and Chord Progressions|Ups and downs]] can name any 8edo chord. Alterations are always enclosed in parentheses, additions never are. An up, down or mid immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13).
 
8edo chords are very ambiguous, with many chord homonyms. Even the major and minor triads are [[Chord homonym|homonyms]]. Chord components usually default to M2, M3, P4, P5, M6, m7, M9, P11 and M13. Thus D7 has a M3, P5 and m7. 8-edo chord names using 24edo subset names are greatly simplified by using different defaults: instead of the conventional M2, M3, P4, P5, M6, m7, M9, P11 and M13, we have  ~2, ^M3, v4, ^5, M6, ~7, ~9, v11 and M13. Thus D7 becomes ^M3, ^5 and ~7.


{| class="wikitable"
{| class="wikitable"
|-
|-
! | Chord edosteps
! Chord edosteps
! | Chord notes
! Chord notes
! | Full name
! Full name
! | Abbreviated name
! Abbreviated name
! | Homonyms
! Homonyms
|-
|-
| | 0 – 3 – 5
| 0 – 3 – 5
| | D ^F♯ ^A
| D ^F♯ ^A
| | D^(^5)
| D^(^5)
| | D
| D
| | ^F♯m or vGm
| ^F♯m or vGm
|-
|-
| | 0 – 2 – 5
| 0 – 2 – 5
| | D F ^A
| D F ^A
| | Dm(^5)
| Dm(^5)
| | Dm
| Dm
| | ^A or vB♭
| ^A or vB♭
|-
|-
| | 0 – 3 – 5 – 7
| 0 – 3 – 5 – 7
| | D ^F♯ ^A ^C
| D ^F♯ ^A ^C
| | D^7(^5)
| D^7(^5)
| | D7
| D7
| | ^F♯m♯11 or vGm♯11
| ^F♯m♯11 or vGm♯11
|-
|-
| | 0 – 3 – 5 – 6
| 0 – 3 – 5 – 6
| | D ^F♯ ^A B
| D ^F♯ ^A B
| | D6(^3,^5)
| D6(^3,^5)
| | D6
| D6
| | Bm7 and vG,♯9
| Bm7 and vG,♯9
|-
|-
| | 0 – 2 – 5 – 7
| 0 – 2 – 5 – 7
| | D F ^A ^C
| D F ^A ^C
| | Dm,~7(^5)
| Dm,~7(^5)
| | Dm7
| Dm7
| | F6 and vB♭,♯9
| F6 and vB♭,♯9
|-
|-
| | 0 – 2 – 5 – 6
| 0 – 2 – 5 – 6
| | D F ^A B
| D F ^A B
| | Dm6(^5)
| Dm6(^5)
| | Dm6
| Dm6
| | Bm7(♭5)
| Bm7(♭5)
|-
|-
| | 0 – 2 – 4 – 7
| 0 – 2 – 4 – 7
| | D F A♭ ^C
| D F A♭ ^C
| | Ddim,~7
| Ddim,~7
| | Dm7(♭5)
| Dm7(♭5)
| | Fm6
| Fm6
|}
|}


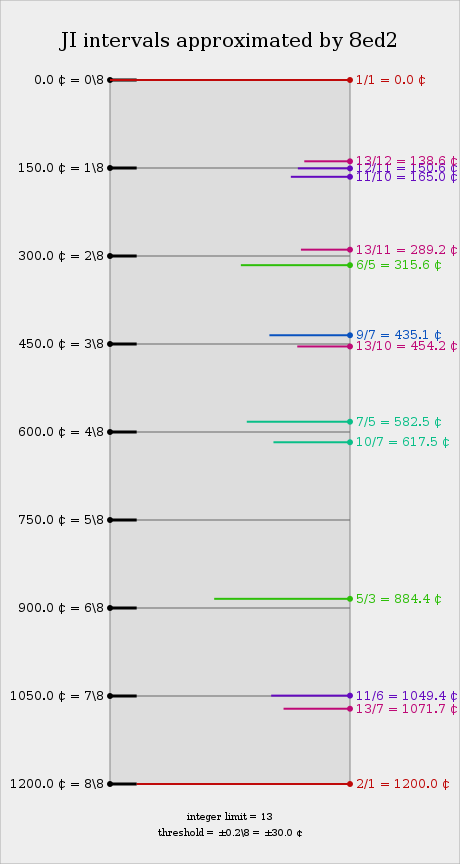
== JI approximation ==
== Approximation to JI ==
[[File:8ed2-001.svg|alt=alt : Your browser has no SVG support.]]
[[File:8ed2-001.svg]]
 
[[:File:8ed2-001.svg|8ed2-001.svg]]


== Regular temperament properties ==
== Regular temperament properties ==
=== Uniform maps ===
=== Uniform maps ===
{{Uniform map|13|7.5|8.5}}
{{Uniform map|edo=8}}


=== Commas ===
=== Commas ===
8edo [[tempers out]] the following [[comma]]s. This assumes [[val]] {{val| 8 13 19 22 28 30 }}.
8et [[tempering out|tempers out]] the following [[comma]]s. This assumes [[val]] {{val| 8 13 19 22 28 30 }}.


{| class="commatable wikitable center-all left-3 right-5 left-6"
{| class="commatable wikitable center-all left-3 right-4 left-6"
! [[Harmonic limit|Prime<br>Limit]]
! [[Harmonic limit|Prime<br />limit]]
! [[Ratio]]<ref>Ratios longer than 10 digits are presented by placeholders with informative hints</ref>
! [[Ratio]]<ref>Ratios longer than 10 digits are presented by placeholders with informative hints</ref>
! [[Monzo]]
! [[Monzo]]
Line 253: Line 394:
| 111.73
| 111.73
| gu 2nd
| gu 2nd
| Classic minor second
| Father comma, classic limma
|-
|-
| 5
| 5
Line 260: Line 401:
| 62.57
| 62.57
| Quadgu
| Quadgu
| Major diesis, diminished comma
| Diminished comma, major diesis
|-
|-
| 5
| 5
Line 267: Line 408:
| 49.17
| 49.17
| Triyo
| Triyo
| Maximal diesis, porcupine comma
| Porcupine comma, maximal diesis
|-
|-
| 5
| 5
Line 274: Line 415:
| 13.40
| 13.40
| Sepgu
| Sepgu
| Medium semicomma, sensipent comma
| Sensipent comma, medium semicomma
|-
|-
| 7
| 7
Line 302: Line 443:
| 5.36
| 5.36
| Sarurutrigu
| Sarurutrigu
| Porwell
| Porwell comma
|-
|-
| 11  
| 11  
Line 344: Line 485:
| 3.03
| 3.03
| Triluyo
| Triluyo
| Wizardharry
| Wizardharry comma
|-
|-
| 13
| 13
Line 351: Line 492:
| 43.83
| 43.83
| Thuyo unison
| Thuyo unison
| tridecimal minor diesis
| Tridecimal minor diesis
|}
|}
<references/>
<references/>


== Scales ==
== Scales ==
=== Scala scale file ===
=== Scala file ===
For those who use the new tuner Lingot, which accepts scala files, or for anyone else, here is a .scl file of 8edo [[:File:08-EDO.scl|08-edo.scl]]
Here is a .scl file of 8edo: [[:File:08-EDO.scl|08-edo.scl]]


<pre>
<pre>
! 08-EDO.scl
! 08-EDO.scl
!
!  
8 EDO
8 EDO
  8
  8
!
!  
  150.00
  150.00
  300.00
  300.00
Line 376: Line 517:


=== Temperaments ===
=== Temperaments ===
8edo is fairly composite, so the only step that generates a [[mos]] scale that covers every interval other than the 1 is the 3, producing scales of 332 and [[3L_2s|21212]]. In terms of temperaments, in the 5-limit this is best interpreted as [[Father_family|Father]], as 8edo is the highest edo that tempers out the diatonic semitone in it's [[patent val]], merging 5/4 and 4/3 into a single interval, which is also the generator. This means major and minor chords are rotations of each other, making them inaccurate but very simple, with even the 5 note mos having 3 of both and providing a functional skeleton of 5-limit harmony, albeit with some very strange enharmonic equivalences. In terms of 7-limit extensions things get even more inaccurate, as the patent val supports [[Father_family#Mother|Mother]], but the ideal tuning for that is much closer to [[5edo]]. The d val supports septimal father and [[Father_family#Pater|Pater]], and is much closer to the ideal tuning for both, as the extremely sharp 7 works better with the 3&5. In terms of multi-period temperaments, it makes for a near perfect [[Jubilismic_clan#Walid|Walid]] or a much less accurate [[Dimipent_family#Diminished|Diminished]] scale.
8edo is fairly composite, so the only step that generates a [[mos]] scale that covers every interval other than the 1 is the 3, producing scales of 332 and [[3L 2s|21212]]. In terms of temperaments, in the 5-limit this is best interpreted as [[father]], as 8edo is the highest edo that tempers out the diatonic semitone in it's [[patent val]], merging 5/4 and 4/3 into a single interval, which is also the generator. This means major and minor chords are rotations of each other, making them inaccurate but very simple, with even the 5 note mos having 3 of both and providing a functional skeleton of 5-limit harmony, albeit with some very strange enharmonic equivalences. In terms of 7-limit extensions things get even more inaccurate, as the patent val supports [[mother]], but the ideal tuning for that is much closer to [[5edo]]. The 8d val supports septimal father and [[pater]], and is much closer to the ideal tuning for both, as the extremely sharp 7 works better with the {{nowrap| 3 & 5 }}. In terms of multi-period temperaments, it makes for a near perfect [[walid]] or a much less accurate [[diminished (temperament)|diminished]] scale.
 
== Instruments ==
A [[Lumatone mapping for 8edo]] is available.


== Music ==
== Music ==
; Cenobyte
; [[Abnormality]]
* [[:File:8edo-pre-improv.ogg|8edo-pre-improv.ogg]] (2011)
* [https://www.youtube.com/watch?v=tqgRYQxsA9U ''mushroom''] (2024)
* [[:File:darkreflections(sketch).ogg|darkreflections(sketch).ogg]] (2011)
 
* [[:File:skiphop(sketch).ogg|skiphop(sketch).ogg]] (2011)
; [[Cenobyte]]
* [[:File:octo-icy-pensive(sketch).ogg|octo-icy-pensive(sketch).ogg]], [[:File:octo-icy-pensive-echo(sketch).ogg|octo-icy-pensive-echo(sketch).ogg]] (2011)
* [[:File:8edo-pre-improv.ogg|8edo-pre-improv]] (2011)
* [[:File:darkreflections(sketch).ogg|darkreflections(sketch)]] (2011)
* [[:File:skiphop(sketch).ogg|skiphop(sketch)]] (2011)
* [[:File:octo-icy-pensive(sketch).ogg|octo-icy-pensive(sketch)]], [[:File:octo-icy-pensive-echo(sketch).ogg|octo-icy-pensive-echo(sketch)]] (2011)


; [[City of the Asleep]]
; [[City of the Asleep]]
* [http://ia600607.us.archive.org/3/items/Transcendissonance/10Malebolge-CityOfTheAsleep.mp3 "Malebolge"], from [https://cityoftheasleep.bandcamp.com/album/transcendissonance ''Transcendissonance''] (2011)
* [http://ia600607.us.archive.org/3/items/Transcendissonance/10Malebolge-CityOfTheAsleep.mp3 "Malebolge"], from [https://cityoftheasleep.bandcamp.com/album/transcendissonance ''Transcendissonance''] (2011)


; Milan Guštar
; [[Milan Guštar]]
* [http://www.uvnitr.cz/flaoyg/forgotten_works/spendliky.html ''Špendlíky''] (1988-2005)
* [http://www.uvnitr.cz/flaoyg/forgotten_works/spendliky.html ''Špendlíky''] (1988-2005)


; Hideya A
; [[Hideya]]
* [https://www.youtube.com/watch?v=dxjBt4Umbw4 ''Like yamashiro''] (2021)
* [https://www.youtube.com/watch?v=dxjBt4Umbw4 ''Like yamashiro''] (2021)
* [https://www.youtube.com/watch?v=h75K1KOb5is ''Like Ensor's paintings''] (2023)
* [https://www.youtube.com/watch?v=h75K1KOb5is ''Like Ensor's paintings''] (2023)
; [[Nathan Ho]]
* [https://www.youtube.com/watch?v=DR1SSW-kQqs ''8edo minimal techno in SuperCollider''] (2023)


; [[Aaron Andrew Hunt]]
; [[Aaron Andrew Hunt]]
* [https://aaronandrewhunt.bandcamp.com/track/fantasia-fugue-a4-in-8et "Fantasia & Fugue a4 in 8ET"], from [https://aaronandrewhunt.bandcamp.com/album/the-equal-tempered-keyboard ''The Equal-Tempered Keyboard''] (1999-2022)
* [https://aaronandrewhunt.bandcamp.com/track/fantasia-fugue-a4-in-8et "Fantasia & Fugue a4 in 8ET"], from [https://aaronandrewhunt.bandcamp.com/album/the-equal-tempered-keyboard ''The Equal-Tempered Keyboard''] (1999-2022)
; [[NullPointerException Music]]
* [https://www.youtube.com/watch?v=CryT-HTzrZE "Disorient"], from [https://www.youtube.com/playlist?list=PLg1YtcJbLxnwTJkG4m0BWZWxIHj7ScdNn ''Edolian''] (2020)
* [https://www.youtube.com/watch?v=AErBW21bljk ''Towards Dissolution''] (2020)
; [[User:Phanomium|Phanomium]]
* [https://www.youtube.com/watch?v=22OKO6e6nGk ''Octahedron''] (2024)


; [[Carlo Serafini]]
; [[Carlo Serafini]]
* [http://www.seraph.it/dep/det/FunkEight1.mp3 ''FunkEight 1''] (2013) ([http://www.seraph.it/blog_files/86557ece0348a8d042346d5e1b13e2d9-166.html details])
* ''FunkEight 1'' (2013) – [http://www.seraph.it/blog_files/86557ece0348a8d042346d5e1b13e2d9-166.html blog] | [http://www.seraph.it/dep/det/FunkEight1.mp3 play]
 
; [[Sevish]]
* [https://youtu.be/1fpYEVEdcaE ''Reckoner''] (2025)


; Jake Sherman
; [[Jake Sherman]]
* [http://www.youtube.com/watch?v=0mpDeL7iybI ''News To Me''] (2011)
* [https://www.youtube.com/watch?v=0mpDeL7iybI ''News To Me''] (2011)
* [http://www.youtube.com/watch?v=HvDEoZ4LIdc ''Tomorrow Night (pop music from 2045)''] (2011)
* [https://www.youtube.com/watch?v=HvDEoZ4LIdc ''Tomorrow Night (pop music from 2045)''] (2011)


; [[Ron Sword]]
; [[Ron Sword]]
Line 413: Line 573:
; [[Randy Winchester]]
; [[Randy Winchester]]
* [https://archive.org/details/jamendo-005173/07.mp3 "7. 8 / octave"], from ''[[Comets Over Flatland]]'' (2007)
* [https://archive.org/details/jamendo-005173/07.mp3 "7. 8 / octave"], from ''[[Comets Over Flatland]]'' (2007)
; [[User:Fitzgerald_Lee|Fitzgerald Lee]]
* [https://youtu.be/zwRDfjLzXkU Jonky Jazz] (2025)


== Ear training ==
== Ear training ==
Line 419: Line 582:
== See also ==
== See also ==
* [[Octatonic scale]] - a scale based on alternating whole and half steps
* [[Octatonic scale]] - a scale based on alternating whole and half steps
* [[Fendo family]] - temperaments closely related to 8edo


[[Category:8edo| ]] <!-- main article -->
[[Category:Equal divisions of the octave|#]] <!-- 1-digit number -->
[[Category:8-tone scales]]
[[Category:8-tone scales]]
[[Category:Listen]]
[[Category:Listen]]
[[Category:Macrotonal]]

Latest revision as of 05:54, 22 August 2025

← 7edo 8edo 9edo →
Prime factorization 23
Step size 150 ¢ 
Fifth 5\8 (750 ¢)
Semitones (A1:m2) 3:-1 (450 ¢ : -150 ¢)
Consistency limit 5
Distinct consistency limit 3

8 equal divisions of the octave (abbreviated 8edo or 8ed2), also called 8-tone equal temperament (8tet) or 8 equal temperament (8et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 8 equal parts of exactly 150 ¢ each. Each step represents a frequency ratio of 21/8, or the 8th root of 2.

Theory

A chromatic 8edo scale on C.

Approximation to JI

8edo forms an odd and even pitch set of two diminished seventh chords, which when used in combination yield dissonance. The system has been described as a "barbaric" harmonic system, containing no good approximation of harmonics 3, 5, 7, 11, 13, and 17; even so, it does a good job representing the just intonation subgroups 2.11/3.13/5, with good intervals of 13/10 and an excellent version of 11/6. Stacking the 450-cent interval can result in some semi-consonant chords such as 0-3-6 degrees, although these still are quite dissonant compared to standard root-3rd-P5 triads, which are unavailable in 8edo.

Another way of looking at 8edo is to treat a chord of 0-1-2-3-4 degrees (0-150-300-450-600 cents) as approximating harmonics 10:11:12:13:14 (~0-165-316-454-583 cents), which is not too implausible if you can buy that 12edo is a 5-limit temperament. This interpretation would imply that 121/120, 144/143, 169/168, and hence also 36/35 and 66/65, are tempered out.

Relationship with the father comma

When 8edo is treated as a very inaccurate 5-limit system, it ends up tempering out the Father comma, 16/15. In fact, it is the largest edo that tempers this comma. What this means is that intervals 16/15 apart in 8edo map to the same note, such as 4/3 being mapped to the same note as 5/4.

Some other odd equivalencies include:

0-2-5: which can be seen as a minor triad (10:12:15), a sus2 triad (9:8:12), or a major triad in first inversion (5:6:8).

0-3-5: which can be seen as a major triad (4:5:6), a sus4 triad (6:8:9), or a minor chord in second inversion (15:20:24).

Odd harmonics

Approximation of odd harmonics in 8edo
Harmonic 3 5 7 9 11 13 15 17 19 21 23
Error Absolute (¢) +48.0 +63.7 -68.8 -53.9 +48.7 +59.5 -38.3 +45.0 +2.5 -20.8 -28.3
Relative (%) +32.0 +42.5 -45.9 -35.9 +32.5 +39.6 -25.5 +30.0 +1.7 -13.9 -18.8
Steps
(reduced) 		13
(5) 		19
(3) 		22
(6) 		25
(1) 		28
(4) 		30
(6) 		31
(7) 		33
(1) 		34
(2) 		35
(3) 		36
(4)

Octave shrinking

8edo's approximation of JI can be improved via octave shrinking. Compressing 8edo's octave from 1200 cents down to 1187 cents gives the tuning called 29ed12.

Of all prime harmonics up to 31, pure-octave 8edo only manages to approximate 2/1 and 19/1 within 15 cents, completely missing all the others.

By contrast, 29ed12 approximates 2/1, 11/1, 13/1, 17/1 and 31/1 all within 15 cents.

Of all integer harmonics up to 30, pure-octave 8edo approximates the following within 20 cents:

  • 2, 4, 8, 16, 19, 27.

Of all integer harmonics up to 30, 29ed12 approximates the following within 20 cents:

  • 2, 6, 11, 12, 13, 17, 20, 22, 25, 26.

This provides 29ed12 with a comparatively larger, more diverse palette of consonances than pure-octaves 8edo.

The nearest zeta peak index tunings to 8edo don't have an interval within 20 cents of 2/1, making them unrecognisable as stretched or compressed 8edo but instead more like entirely new scales in their own right.

Subsets and supersets

8edo contains 2edo and 4edo as subsets. Among its supersets are 16edo, 24edo, 32edo, ….

Intervals

Steps Cents JI approximation Other
2.11/3.13/5.19* 2.5/3.11/3.13/5* 10:11:12:13:14* Patent val ⟨8 13 19]
0 0 1/1 1/1 1/1 1/1, 16/15
1 150 12/11 12/11 12/11, 11/10 10/9, 25/24
2 300 19/16 6/5 6/5 6/5, 9/8
3 450 13/10 13/10 13/10 4/3, 5/4
4 600 7/5, 10/7 27/20, 25/18, 36/25
5 750 20/13 20/13 20/13 3/2, 8/5
6 900 32/19 5/3 5/3 5/3, 16/9
7 1050 11/6 11/6 20/11, 11/6 9/5, 48/50
8 1200 2/1 2/1 2/1 2/1, 15/8

* Allows inversion by 2/1; other interpretations also possible

Notation

Ups and downs notation

8edo can be notated as a subset of 24edo, using ups and downs. It can also be notated as a subset of 16edo, but this is a less intuitive notation.

Edostep Cents 24edo subset notation
(EUs: vvA1 and d2) 		16edo subset notation
(major narrower than minor) 		16edo subset notation
(major wider than minor) 		3L 2s notation
(J = 1/1) 		Audio
0 0¢ P1 D P1 D P1 D J
1 150 ~2 vE M2 E m2 E K
2 300 m3 F M3 F# m3 Fb K#, Lb
3 450 ^M3 / v4 ^F# / vG d3 / A4 Fb / G# A3, D4 F#, Gb L
4 600 A4, d5 G#, Ab d4, A5 Gb, A# A4, D5 G#, Ab M
5 750 ^5, vm6 ^A, vBb d5, A6 Ab, B# A5, d6 A#, Bb M#, Nb
6 900 M6 B m6 Bb M6 B# N
7 1050 ~7 ^C m7 C M7 C N#, Jb
8 1200 P8 D P8 D P8 D J

This is a heptatonic notation generated by 5ths (5th meaning 3/2). Alternative notations include pentatonic 5th-generated, octatonic, and heptatonic 2nd-generated.

Pentatonic 5th-generated: D * E G * A C * D (generator = 5\8 = perfect 5thoid)

D - D#/Eb - E - G - G#/Ab - A - C - C#/Db - D

P1 - A1/ms3 - Ms3 - P4d - A4d/d5d - P5d - ms7 - Ms7/d8d - P8d (s = sub-, d = -oid, see 5edo notation)

pentatonic genchain of 5ths: ...Cb - Gb - Db - Ab - Eb - C - G - D - A - E - C# - G# - D# - A# - E#...

pentatonic genchain of 5ths: ...d8d - d5d - ms3 - ms7 - P4d - P1 - P5d - Ms3 - Ms7 - A4d - A1... (s = sub-, d = -oid)

Enharmonic unison: ds3

Octatonic: A B C D E F G H A (every interval is a generator)

P1 - P2 - P3 - P4 - P5 - P6 - P7 - P8 - P9

Enharmonic unison: none

Heptatonic 2nd-generated: D E F G * A B C D (generator = 1\8 = perfect 2nd = 150¢)

D - E - F - G - G#/Ab - A -B - C - D

P1 - P2 - m3 - M3/m4 - M4/m5 - M5/m6 - M6 - P7 - P8

genchain of 2nds: ...D# - E# - F# - G# - A - B - C - D - E - F - G - Ab - Bb - Cb - Db...

genchain of 2nds: ...A1 - A2 - M3 - M4 - M5 - M6 - P7 - P1 - P2 - m3 - m4 - m5 - m6 - d7 - d8...

Enharmonic unison: d2

Sagittal notation

This notation is a subset of the notations for EDOs 24, 48, and 72.

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation24-EDO notation

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation24-EDO notation

Evo-SZ flavor

Sagittal notationPeriodic table of EDOs with sagittal notation24-EDO notation

Because it contains no Sagittal symbols, this Evo-SZ Sagittal notation is also a Stein-Zimmerman notation.

Chord names

Ups and downs can name any 8edo chord. Alterations are always enclosed in parentheses, additions never are. An up, down or mid immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13).

8edo chords are very ambiguous, with many chord homonyms. Even the major and minor triads are homonyms. Chord components usually default to M2, M3, P4, P5, M6, m7, M9, P11 and M13. Thus D7 has a M3, P5 and m7. 8-edo chord names using 24edo subset names are greatly simplified by using different defaults: instead of the conventional M2, M3, P4, P5, M6, m7, M9, P11 and M13, we have ~2, ^M3, v4, ^5, M6, ~7, ~9, v11 and M13. Thus D7 becomes ^M3, ^5 and ~7.

Chord edosteps Chord notes Full name Abbreviated name Homonyms
0 – 3 – 5 D ^F♯ ^A D^(^5) D ^F♯m or vGm
0 – 2 – 5 D F ^A Dm(^5) Dm ^A or vB♭
0 – 3 – 5 – 7 D ^F♯ ^A ^C D^7(^5) D7 ^F♯m♯11 or vGm♯11
0 – 3 – 5 – 6 D ^F♯ ^A B D6(^3,^5) D6 Bm7 and vG,♯9
0 – 2 – 5 – 7 D F ^A ^C Dm,~7(^5) Dm7 F6 and vB♭,♯9
0 – 2 – 5 – 6 D F ^A B Dm6(^5) Dm6 Bm7(♭5)
0 – 2 – 4 – 7 D F A♭ ^C Ddim,~7 Dm7(♭5) Fm6

Approximation to JI

Regular temperament properties

Uniform maps

13-limit uniform maps between 7.8 and 8.2
Min. size Max. size Wart notation Map
7.7018 7.8866 8bcef ⟨8 12 18 22 27 29]
7.8866 7.9493 8cef ⟨8 13 18 22 27 29]
7.9493 7.9675 8cf ⟨8 13 18 22 28 29]
7.9675 7.9720 8f ⟨8 13 19 22 28 29]
7.9720 8.0147 8 ⟨8 13 19 22 28 30]
8.0147 8.2383 8d ⟨8 13 19 23 28 30]

Commas

8et tempers out the following commas. This assumes val ⟨8 13 19 22 28 30].

Prime
limit 		Ratio[1] Monzo Cents Color name Name(s)
3 8192/6561 [13 -8⟩ 384.35 sawa 4th Pythagorean diminished fourth
5 16/15 [4 -1 -1⟩ 111.73 gu 2nd Father comma, classic limma
5 648/625 [3 4 -4⟩ 62.57 Quadgu Diminished comma, major diesis
5 250/243 [1 -5 3⟩ 49.17 Triyo Porcupine comma, maximal diesis
5 78732/78125 [2 9 -7⟩ 13.40 Sepgu Sensipent comma, medium semicomma
7 64/63 [6 -2 0 -1⟩ 27.26 Ru Septimal comma, Archytas' comma, Leipziger Komma
7 875/864 [-5 -3 3 1⟩ 21.90 Zotriyo Keema
7 (12 digits) [-9 8 -4 2⟩ 8.04 Labizogugu Varunisma
7 6144/6125 [11 1 -3 -2⟩ 5.36 Sarurutrigu Porwell comma
11 100/99 [2 -2 2 0 -1⟩ 17.40 Luyoyo Ptolemisma
11 121/120 [-3 -1 -1 0 2⟩ 14.37 Lologu Biyatisma
11 176/175 [4 0 -2 -1 1⟩ 9.86 Lorugugu Valinorsma
11 65536/65219 [16 0 0 -2 -3⟩ 8.39 Satrilu-aruru Orgonisma
11 385/384 [-7 -1 1 1 1⟩ 4.50 Lozoyo Keenanisma
11 4000/3993 [5 -1 3 0 -3⟩ 3.03 Triluyo Wizardharry comma
13 40/39 [3 -1 1 0 0 -1⟩ 43.83 Thuyo unison Tridecimal minor diesis
  1. ↑ Ratios longer than 10 digits are presented by placeholders with informative hints

Scales

Scala file

Here is a .scl file of 8edo: 08-edo.scl 

! 08-EDO.scl
! 
8 EDO
 8
! 
 150.00
 300.00
 450.00
 600.00
 750.00
 900.00
 1050.00
 2/1

Temperaments

8edo is fairly composite, so the only step that generates a mos scale that covers every interval other than the 1 is the 3, producing scales of 332 and 21212. In terms of temperaments, in the 5-limit this is best interpreted as father, as 8edo is the highest edo that tempers out the diatonic semitone in it's patent val, merging 5/4 and 4/3 into a single interval, which is also the generator. This means major and minor chords are rotations of each other, making them inaccurate but very simple, with even the 5 note mos having 3 of both and providing a functional skeleton of 5-limit harmony, albeit with some very strange enharmonic equivalences. In terms of 7-limit extensions things get even more inaccurate, as the patent val supports mother, but the ideal tuning for that is much closer to 5edo. The 8d val supports septimal father and pater, and is much closer to the ideal tuning for both, as the extremely sharp 7 works better with the 3 & 5. In terms of multi-period temperaments, it makes for a near perfect walid or a much less accurate diminished scale.

Instruments

A Lumatone mapping for 8edo is available.

Music

Abnormality
Cenobyte
City of the Asleep
Milan Guštar
Hideya
Nathan Ho
Aaron Andrew Hunt
NullPointerException Music
Phanomium
Carlo Serafini
Sevish
Jake Sherman
Ron Sword
Stephen Weigel
Randy Winchester
Fitzgerald Lee

Ear training

8edo ear-training exercises by Alex Ness available here.

See also

Retrieved from "https://en.xen.wiki/index.php?title=8edo&oldid=208018"