8edo: Difference between revisions
Wikispaces>genewardsmith **Imported revision 246408139 - Original comment: ** |
→Octave shrinking: Temporary improvement until the new standard is rolled out |
||
| (132 intermediate revisions by 39 users not shown) | |||
| Line 1: | Line 1: | ||
{{interwiki | |||
| de = 8edo | |||
| en = 8edo | |||
| es = | |||
| ja = 8平均律 | |||
}} | |||
{{Infobox ET}} | |||
{{ED intro}} | |||
== Theory == | |||
[[File:8edo scale.mp3|thumb|A chromatic 8edo scale on C.]] | |||
=== Approximation to JI === | |||
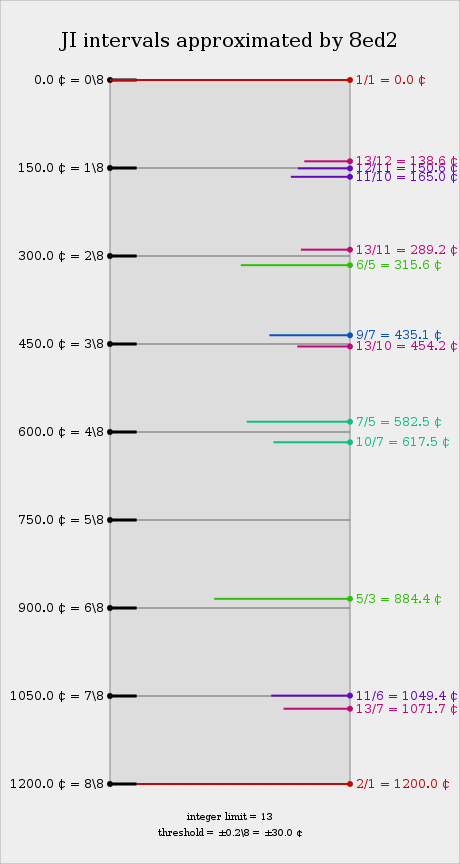
8edo forms an odd and even pitch set of two diminished seventh chords, which when used in combination yield dissonance. The system has been described as a "barbaric" harmonic system, containing no good approximation of harmonics 3, 5, 7, 11, 13, and 17; even so, it does a good job representing the [[just intonation subgroup]]s 2.11/3.13/5, with good intervals of [[13/10]] and an excellent version of [[11/6]]. Stacking the 450-cent interval can result in some semi-consonant chords such as 0-3-6 degrees, although these still are quite dissonant compared to standard root-3rd-P5 triads, which are unavailable in 8edo. | |||
Another way of looking at 8edo is to treat a chord of 0-1-2-3-4 degrees (0-150-300-450-600 cents) as approximating harmonics 10:11:12:13:14 (~0-165-316-454-583 cents), which is not too implausible if you can buy that 12edo is a 5-limit temperament. This interpretation would imply that 121/120, 144/143, 169/168, and hence also 36/35 and 66/65, are tempered out. | |||
=== Relationship with the father comma === | |||
When 8edo is treated as a very inaccurate 5-limit system, it ends up tempering out the [[Father]] comma, [[16/15]]. In fact, it is the largest edo that tempers this comma. What this means is that intervals 16/15 apart in 8edo map to the same note, such as [[4/3]] being mapped to the same note as [[5/4]]. | |||
Some other odd equivalencies include: | |||
0 | '''0-2-5''': which can be seen as a minor triad (10:12:15), a sus2 triad (9:8:12), or a major triad in first inversion (5:6:8). | ||
5 | |||
6 | |||
'''0-3-5''': which can be seen as a major triad (4:5:6), a sus4 triad (6:8:9), or a minor chord in second inversion (15:20:24). | |||
=== Odd harmonics === | |||
{{Harmonics in equal|8|intervals=odd}} | |||
= | === Octave shrinking === | ||
8edo's approximation of [[JI]] can be improved via [[octave shrinking]]. Compressing 8edo's octave from 1200 [[cent]]s down to 1187 cents gives the tuning called [[29ed12]]. | |||
Of all prime [[harmonic]]s up to 31, pure-octave 8edo only manages to approximate 2/1 and 19/1 within 15 [[cents]], completely missing all the others. | |||
By contrast, 29ed12 approximates 2/1, 11/1, 13/1, 17/1 and 31/1 all within 15 cents. | |||
Of all integer harmonics up to 30, pure-octave 8edo approximates the following within 20 cents: | |||
* 2, 4, 8, 16, 19, 27. | |||
Of all integer harmonics up to 30, 29ed12 approximates the following within 20 cents: | |||
* 2, 6, 11, 12, 13, 17, 20, 22, 25, 26. | |||
This provides 29ed12 with a comparatively larger, more diverse palette of [[consonance]]s than pure-octaves 8edo. | |||
The nearest [[zeta peak index]] tunings to 8edo don't have an interval within 20 cents of [[2/1]], making them unrecognisable as stretched or compressed 8edo but instead more like entirely new scales in their own right. | |||
=== Subsets and supersets === | |||
8edo contains [[2edo]] and [[4edo]] as subsets. Among its supersets are [[16edo]], [[24edo]], [[32edo]], …. | |||
== Intervals == | |||
{| class="wikitable" | |||
|- | |||
! rowspan="2" | Steps | |||
! rowspan="2" | Cents | |||
! colspan="3" | JI approximation | |||
!Other | |||
|- | |||
! 2.11/3.13/5.19* | |||
! 2.5/3.11/3.13/5* | |||
! 10:11:12:13:14* | |||
!Patent val ⟨8 13 19] | |||
|- | |||
| 0 | |||
| 0 | |||
| 1/1 | |||
| 1/1 | |||
| 1/1 | |||
|1/1, 16/15 | |||
|- | |||
| 1 | |||
| 150 | |||
| 12/11 | |||
| 12/11 | |||
| 12/11, 11/10 | |||
|10/9, 25/24 | |||
|- | |||
| 2 | |||
| 300 | |||
| 19/16 | |||
| 6/5 | |||
| 6/5 | |||
|6/5, 9/8 | |||
|- | |||
| 3 | |||
| 450 | |||
| 13/10 | |||
| 13/10 | |||
| 13/10 | |||
|4/3, 5/4 | |||
|- | |||
| 4 | |||
| 600 | |||
| | |||
| | |||
| 7/5, 10/7 | |||
|27/20, 25/18, 36/25 | |||
|- | |||
| 5 | |||
| 750 | |||
| 20/13 | |||
| 20/13 | |||
| 20/13 | |||
|3/2, 8/5 | |||
|- | |||
| 6 | |||
| 900 | |||
| 32/19 | |||
| 5/3 | |||
| 5/3 | |||
|5/3, 16/9 | |||
|- | |||
| 7 | |||
| 1050 | |||
| 11/6 | |||
| 11/6 | |||
| 20/11, 11/6 | |||
|9/5, 48/50 | |||
|- | |||
| 8 | |||
| 1200 | |||
| 2/1 | |||
| 2/1 | |||
| 2/1 | |||
|2/1, 15/8 | |||
|} | |||
<nowiki />* Allows [[inversion]] by 2/1; other interpretations also possible | |||
== Notation == | |||
=== Ups and downs notation === | |||
8edo can be notated as a subset of 24edo, using [[Ups and downs notation|ups and downs]]. It can also be notated as a subset of 16edo, but this is a less intuitive notation. | |||
{| class="wikitable center-all" | |||
|- | |||
! Edostep | |||
! [[Cent]]s | |||
! colspan="2" | 24edo subset notation<br />([[Enharmonic unisons in ups and downs notation|EUs:]] vvA1 and d2) | |||
! colspan="2" | 16edo subset notation<br />(major narrower than minor) | |||
! colspan="2" | 16edo subset notation<br />(major wider than minor) | |||
! [[3L 2s]] notation<br />({{nowrap|J {{=}} 1/1}}) | |||
! Audio | |||
|- | |||
| 0 | |||
| 0¢ | |||
| P1 | |||
| D | |||
| P1 | |||
| D | |||
| P1 | |||
| D | |||
| J | |||
| [[File:0-0 unison.mp3|frameless]] | |||
|- | |||
| 1 | |||
| 150 | |||
| ~2 | |||
| vE | |||
| M2 | |||
| E | |||
| m2 | |||
| E | |||
| K | |||
| [[File:0-150 (8-EDO).mp3|frameless]] | |||
|- | |||
| 2 | |||
| 300 | |||
| m3 | |||
| F | |||
| M3 | |||
| F# | |||
| m3 | |||
| Fb | |||
| K#, Lb | |||
| [[File:0-300 (12-EDO).mp3|frameless]] | |||
|- | |||
| 3 | |||
| 450 | |||
| ^M3 / v4 | |||
| ^F# / vG | |||
| d3 / A4 | |||
| Fb / G# | |||
| A3, D4 | |||
| F#, Gb | |||
| L | |||
| [[File:0-450 (8-EDO).mp3|frameless]] | |||
|- | |||
| 4 | |||
| 600 | |||
| A4, d5 | |||
| G#, Ab | |||
| d4, A5 | |||
| Gb, A# | |||
| A4, D5 | |||
| G#, Ab | |||
| M | |||
| [[File:0-600 (12-EDO).mp3|frameless]] | |||
|- | |||
| 5 | |||
| 750 | |||
| ^5, vm6 | |||
| ^A, vBb | |||
| d5, A6 | |||
| Ab, B# | |||
| A5, d6 | |||
| A#, Bb | |||
| M#, Nb | |||
| [[File:0-750 (8-EDO).mp3|frameless]] | |||
|- | |||
| 6 | |||
| 900 | |||
| M6 | |||
| B | |||
| m6 | |||
| Bb | |||
| M6 | |||
| B# | |||
| N | |||
| [[File:0-900 (12-EDO).mp3|frameless]] | |||
|- | |||
| 7 | |||
| 1050 | |||
| ~7 | |||
| ^C | |||
| m7 | |||
| C | |||
| M7 | |||
| C | |||
| N#, Jb | |||
| [[File:0-1050 (8-EDO).mp3|frameless]] | |||
|- | |||
| 8 | |||
| 1200 | |||
| P8 | |||
| D | |||
| P8 | |||
| D | |||
| P8 | |||
| D | |||
| J | |||
| [[File:0-1200 octave.mp3|frameless]] | |||
|} | |||
This is a heptatonic notation generated by 5ths (5th meaning 3/2). Alternative notations include pentatonic 5th-generated, octatonic, and heptatonic 2nd-generated. | |||
'''<u>Pentatonic 5th-generated</u>: D * E G * A C * D''' (generator = 5\8 = perfect 5thoid) | |||
D - D#/Eb - E - G - G#/Ab - A - C - C#/Db - D | |||
P1 - A1/ms3 - Ms3 - P4d - A4d/d5d - P5d - ms7 - Ms7/d8d - P8d (s = sub-, d = -oid, see [[5edo#Alternative notations|5edo]] notation) | |||
pentatonic genchain of 5ths: ...Cb - Gb - Db - Ab - Eb - C - G - D - A - E - C# - G# - D# - A# - E#... | |||
pentatonic genchain of 5ths: ...d8d - d5d - ms3 - ms7 - P4d - P1 - P5d - Ms3 - Ms7 - A4d - A1... (s = sub-, d = -oid) | |||
[[Enharmonic unison]]: ds3 | |||
'''<u>Octatonic:</u>''' '''A B C D E F G H A''' (every interval is a generator) | |||
P1 - P2 - P3 - P4 - P5 - P6 - P7 - P8 - P9 | |||
Enharmonic unison: none | |||
'''<u>Heptatonic 2nd-generated</u>: D E F G * A B C D''' (generator = 1\8 = perfect 2nd = 150¢) | |||
D - E - F - G - G#/Ab - A -B - C - D | |||
P1 - P2 - m3 - M3/m4 - M4/m5 - M5/m6 - M6 - P7 - P8 | |||
genchain of 2nds: ...D# - E# - F# - G# - A - B - C - D - E - F - G - Ab - Bb - Cb - Db... | |||
genchain of 2nds: ...A1 - A2 - M3 - M4 - M5 - M6 - P7 - P1 - P2 - m3 - m4 - m5 - m6 - d7 - d8... | |||
Enharmonic unison: d2 | |||
===Sagittal notation=== | |||
This notation is a subset of the notations for EDOs [[24edo#Sagittal notation|24]], [[48edo#Sagittal notation|48]], and [[72edo#Sagittal notation|72]]. | |||
====Evo flavor==== | |||
<imagemap> | |||
File:8-EDO_Evo_Sagittal.svg | |||
desc none | |||
rect 80 0 300 50 [[Sagittal_notation]] | |||
rect 392 0 552 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation] | |||
rect 20 80 392 106 [[24-EDO#Sagittal_notation | 24-EDO notation]] | |||
default [[File:8-EDO_Evo_Sagittal.svg]] | |||
</imagemap> | |||
====Revo flavor==== | |||
<imagemap> | |||
File:8-EDO_Revo_Sagittal.svg | |||
desc none | |||
rect 80 0 300 50 [[Sagittal_notation]] | |||
rect 400 0 560 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation] | |||
rect 20 80 400 106 [[24-EDO#Sagittal_notation | 24-EDO notation]] | |||
default [[File:8-EDO_Revo_Sagittal.svg]] | |||
</imagemap> | |||
====Evo-SZ flavor==== | |||
<imagemap> | |||
File:8-EDO_Evo-SZ_Sagittal.svg | |||
desc none | |||
rect 80 0 300 50 [[Sagittal_notation]] | |||
rect 376 0 536 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation] | |||
rect 20 80 376 106 [[24-EDO#Sagittal_notation | 24-EDO notation]] | |||
default [[File:8-EDO_Evo-SZ_Sagittal.svg]] | |||
</imagemap> | |||
Because it contains no Sagittal symbols, this Evo-SZ Sagittal notation is also a Stein-Zimmerman notation. | |||
== Chord names == | |||
[[Ups and downs notation #Chords and Chord Progressions|Ups and downs]] can name any 8edo chord. Alterations are always enclosed in parentheses, additions never are. An up, down or mid immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13). | |||
8edo chords are very ambiguous, with many chord homonyms. Even the major and minor triads are [[Chord homonym|homonyms]]. Chord components usually default to M2, M3, P4, P5, M6, m7, M9, P11 and M13. Thus D7 has a M3, P5 and m7. 8-edo chord names using 24edo subset names are greatly simplified by using different defaults: instead of the conventional M2, M3, P4, P5, M6, m7, M9, P11 and M13, we have ~2, ^M3, v4, ^5, M6, ~7, ~9, v11 and M13. Thus D7 becomes ^M3, ^5 and ~7. | |||
{| class="wikitable" | |||
|- | |||
! Chord edosteps | |||
! Chord notes | |||
! Full name | |||
! Abbreviated name | |||
! Homonyms | |||
|- | |||
| 0 – 3 – 5 | |||
| D ^F♯ ^A | |||
| D^(^5) | |||
| D | |||
| ^F♯m or vGm | |||
|- | |||
| 0 – 2 – 5 | |||
| D F ^A | |||
| Dm(^5) | |||
| Dm | |||
| ^A or vB♭ | |||
|- | |||
| 0 – 3 – 5 – 7 | |||
| D ^F♯ ^A ^C | |||
| D^7(^5) | |||
| D7 | |||
| ^F♯m♯11 or vGm♯11 | |||
|- | |||
| 0 – 3 – 5 – 6 | |||
| D ^F♯ ^A B | |||
| D6(^3,^5) | |||
| D6 | |||
| Bm7 and vG,♯9 | |||
|- | |||
| 0 – 2 – 5 – 7 | |||
| D F ^A ^C | |||
| Dm,~7(^5) | |||
| Dm7 | |||
| F6 and vB♭,♯9 | |||
|- | |||
| 0 – 2 – 5 – 6 | |||
| D F ^A B | |||
| Dm6(^5) | |||
| Dm6 | |||
| Bm7(♭5) | |||
|- | |||
| 0 – 2 – 4 – 7 | |||
| D F A♭ ^C | |||
| Ddim,~7 | |||
| Dm7(♭5) | |||
| Fm6 | |||
|} | |||
== Approximation to JI == | |||
[[File:8ed2-001.svg]] | |||
== Regular temperament properties == | |||
=== Uniform maps === | |||
{{Uniform map|edo=8}} | |||
=== Commas === | |||
8et [[tempering out|tempers out]] the following [[comma]]s. This assumes [[val]] {{val| 8 13 19 22 28 30 }}. | |||
{| class="commatable wikitable center-all left-3 right-4 left-6" | |||
! [[Harmonic limit|Prime<br />limit]] | |||
! [[Ratio]]<ref>Ratios longer than 10 digits are presented by placeholders with informative hints</ref> | |||
! [[Monzo]] | |||
! [[Cent]]s | |||
! [[Color name]] | |||
! Name(s) | |||
|- | |||
| 3 | |||
| [[8192/6561]] | |||
| {{monzo| 13 -8 }} | |||
| 384.35 | |||
| sawa 4th | |||
| Pythagorean diminished fourth | |||
|- | |||
| 5 | |||
| [[16/15]] | |||
| {{monzo| 4 -1 -1 }} | |||
| 111.73 | |||
| gu 2nd | |||
| Father comma, classic limma | |||
|- | |||
| 5 | |||
| [[648/625]] | |||
| {{monzo| 3 4 -4 }} | |||
| 62.57 | |||
| Quadgu | |||
| Diminished comma, major diesis | |||
|- | |||
| 5 | |||
| [[250/243]] | |||
| {{monzo| 1 -5 3 }} | |||
| 49.17 | |||
| Triyo | |||
| Porcupine comma, maximal diesis | |||
|- | |||
| 5 | |||
| [[78732/78125]] | |||
| {{monzo| 2 9 -7 }} | |||
| 13.40 | |||
| Sepgu | |||
| Sensipent comma, medium semicomma | |||
|- | |||
| 7 | |||
| [[64/63]] | |||
| {{monzo| 6 -2 0 -1 }} | |||
| 27.26 | |||
| Ru | |||
| Septimal comma, Archytas' comma, Leipziger Komma | |||
|- | |||
| 7 | |||
| [[875/864]] | |||
| {{monzo| -5 -3 3 1 }} | |||
| 21.90 | |||
| Zotriyo | |||
| Keema | |||
|- | |||
| 7 | |||
| <abbr title="321489/320000">(12 digits)</abbr> | |||
| {{monzo| -9 8 -4 2 }} | |||
| 8.04 | |||
| Labizogugu | |||
| [[Varunisma]] | |||
|- | |||
| 7 | |||
| [[6144/6125]] | |||
| {{monzo| 11 1 -3 -2 }} | |||
| 5.36 | |||
| Sarurutrigu | |||
| Porwell comma | |||
|- | |||
| 11 | |||
| [[100/99]] | |||
| {{monzo| 2 -2 2 0 -1 }} | |||
| 17.40 | |||
| Luyoyo | |||
| Ptolemisma | |||
|- | |||
| 11 | |||
| [[121/120]] | |||
| {{monzo| -3 -1 -1 0 2 }} | |||
| 14.37 | |||
| Lologu | |||
| Biyatisma | |||
|- | |||
| 11 | |||
| [[176/175]] | |||
| {{monzo| 4 0 -2 -1 1 }} | |||
| 9.86 | |||
| Lorugugu | |||
| Valinorsma | |||
|- | |||
| 11 | |||
| [[65536/65219]] | |||
| {{monzo| 16 0 0 -2 -3 }} | |||
| 8.39 | |||
| Satrilu-aruru | |||
| Orgonisma | |||
|- | |||
| 11 | |||
| [[385/384]] | |||
| {{monzo| -7 -1 1 1 1 }} | |||
| 4.50 | |||
| Lozoyo | |||
| Keenanisma | |||
|- | |||
| 11 | |||
| [[4000/3993]] | |||
| {{monzo| 5 -1 3 0 -3 }} | |||
| 3.03 | |||
| Triluyo | |||
| Wizardharry comma | |||
|- | |||
| 13 | |||
| [[40/39]] | |||
| {{monzo| 3 -1 1 0 0 -1 }} | |||
| 43.83 | |||
| Thuyo unison | |||
| Tridecimal minor diesis | |||
|} | |||
<references/> | |||
== Scales == | |||
=== Scala file === | |||
Here is a .scl file of 8edo: [[:File:08-EDO.scl|08-edo.scl]] | |||
<pre> | |||
! 08-EDO.scl | |||
! | |||
8 EDO | |||
8 | |||
! | |||
150.00 | |||
300.00 | |||
450.00 | |||
600.00 | |||
750.00 | |||
900.00 | |||
1050.00 | |||
2/1 | |||
</pre> | |||
=== Temperaments === | |||
8edo is fairly composite, so the only step that generates a [[mos]] scale that covers every interval other than the 1 is the 3, producing scales of 332 and [[3L 2s|21212]]. In terms of temperaments, in the 5-limit this is best interpreted as [[father]], as 8edo is the highest edo that tempers out the diatonic semitone in it's [[patent val]], merging 5/4 and 4/3 into a single interval, which is also the generator. This means major and minor chords are rotations of each other, making them inaccurate but very simple, with even the 5 note mos having 3 of both and providing a functional skeleton of 5-limit harmony, albeit with some very strange enharmonic equivalences. In terms of 7-limit extensions things get even more inaccurate, as the patent val supports [[mother]], but the ideal tuning for that is much closer to [[5edo]]. The 8d val supports septimal father and [[pater]], and is much closer to the ideal tuning for both, as the extremely sharp 7 works better with the {{nowrap| 3 & 5 }}. In terms of multi-period temperaments, it makes for a near perfect [[walid]] or a much less accurate [[diminished (temperament)|diminished]] scale. | |||
== Instruments == | |||
A [[Lumatone mapping for 8edo]] is available. | |||
== Music == | |||
; [[Abnormality]] | |||
* [https://www.youtube.com/watch?v=tqgRYQxsA9U ''mushroom''] (2024) | |||
; [[Cenobyte]] | |||
* [[:File:8edo-pre-improv.ogg|8edo-pre-improv]] (2011) | |||
* [[:File:darkreflections(sketch).ogg|darkreflections(sketch)]] (2011) | |||
* [[:File:skiphop(sketch).ogg|skiphop(sketch)]] (2011) | |||
* [[:File:octo-icy-pensive(sketch).ogg|octo-icy-pensive(sketch)]], [[:File:octo-icy-pensive-echo(sketch).ogg|octo-icy-pensive-echo(sketch)]] (2011) | |||
; [[City of the Asleep]] | |||
* [http://ia600607.us.archive.org/3/items/Transcendissonance/10Malebolge-CityOfTheAsleep.mp3 "Malebolge"], from [https://cityoftheasleep.bandcamp.com/album/transcendissonance ''Transcendissonance''] (2011) | |||
; [[Milan Guštar]] | |||
* [http://www.uvnitr.cz/flaoyg/forgotten_works/spendliky.html ''Špendlíky''] (1988-2005) | |||
; [[Hideya]] | |||
* [https://www.youtube.com/watch?v=dxjBt4Umbw4 ''Like yamashiro''] (2021) | |||
* [https://www.youtube.com/watch?v=h75K1KOb5is ''Like Ensor's paintings''] (2023) | |||
; [[Nathan Ho]] | |||
* [https://www.youtube.com/watch?v=DR1SSW-kQqs ''8edo minimal techno in SuperCollider''] (2023) | |||
; [[Aaron Andrew Hunt]] | |||
* [https://aaronandrewhunt.bandcamp.com/track/fantasia-fugue-a4-in-8et "Fantasia & Fugue a4 in 8ET"], from [https://aaronandrewhunt.bandcamp.com/album/the-equal-tempered-keyboard ''The Equal-Tempered Keyboard''] (1999-2022) | |||
; [[NullPointerException Music]] | |||
* [https://www.youtube.com/watch?v=CryT-HTzrZE "Disorient"], from [https://www.youtube.com/playlist?list=PLg1YtcJbLxnwTJkG4m0BWZWxIHj7ScdNn ''Edolian''] (2020) | |||
* [https://www.youtube.com/watch?v=AErBW21bljk ''Towards Dissolution''] (2020) | |||
; [[User:Phanomium|Phanomium]] | |||
* [https://www.youtube.com/watch?v=22OKO6e6nGk ''Octahedron''] (2024) | |||
; [[Carlo Serafini]] | |||
* ''FunkEight 1'' (2013) – [http://www.seraph.it/blog_files/86557ece0348a8d042346d5e1b13e2d9-166.html blog] | [http://www.seraph.it/dep/det/FunkEight1.mp3 play] | |||
; [[Sevish]] | |||
* [https://youtu.be/1fpYEVEdcaE ''Reckoner''] (2025) | |||
; [[Jake Sherman]] | |||
* [https://www.youtube.com/watch?v=0mpDeL7iybI ''News To Me''] (2011) | |||
* [https://www.youtube.com/watch?v=HvDEoZ4LIdc ''Tomorrow Night (pop music from 2045)''] (2011) | |||
; [[Ron Sword]] | |||
* [http://www.ronsword.com/sounds/ronsword_8edo_improv.mp3 ''Acoustic Improvisation in 8EDO'']{{dead link}} | |||
; [[Stephen Weigel]] | |||
* [https://soundcloud.com/overtoneshock/tenacious-chorale-9-edo-and-8-edo-live ''Tenacious Chorale'': Movement 2] (2016) | |||
; [[Randy Winchester]] | |||
* [https://archive.org/details/jamendo-005173/07.mp3 "7. 8 / octave"], from ''[[Comets Over Flatland]]'' (2007) | |||
; [[User:Fitzgerald_Lee|Fitzgerald Lee]] | |||
* [https://youtu.be/zwRDfjLzXkU Jonky Jazz] (2025) | |||
== Ear training == | |||
8edo ear-training exercises by Alex Ness available [https://drive.google.com/a/playgroundsessions.com/folderview?id=0BwsXD8q2VCYUamtVWEgyRFA5alU&usp=sharing#list here]. | |||
== See also == | |||
* [[Octatonic scale]] - a scale based on alternating whole and half steps | |||
* [[Fendo family]] - temperaments closely related to 8edo | |||
[[Category:8-tone scales]] | |||
[[Category:Listen]] | |||
Latest revision as of 05:54, 22 August 2025
| ← 7edo | 8edo | 9edo → |
8 equal divisions of the octave (abbreviated 8edo or 8ed2), also called 8-tone equal temperament (8tet) or 8 equal temperament (8et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 8 equal parts of exactly 150 ¢ each. Each step represents a frequency ratio of 21/8, or the 8th root of 2.
Theory
Approximation to JI
8edo forms an odd and even pitch set of two diminished seventh chords, which when used in combination yield dissonance. The system has been described as a "barbaric" harmonic system, containing no good approximation of harmonics 3, 5, 7, 11, 13, and 17; even so, it does a good job representing the just intonation subgroups 2.11/3.13/5, with good intervals of 13/10 and an excellent version of 11/6. Stacking the 450-cent interval can result in some semi-consonant chords such as 0-3-6 degrees, although these still are quite dissonant compared to standard root-3rd-P5 triads, which are unavailable in 8edo.
Another way of looking at 8edo is to treat a chord of 0-1-2-3-4 degrees (0-150-300-450-600 cents) as approximating harmonics 10:11:12:13:14 (~0-165-316-454-583 cents), which is not too implausible if you can buy that 12edo is a 5-limit temperament. This interpretation would imply that 121/120, 144/143, 169/168, and hence also 36/35 and 66/65, are tempered out.
Relationship with the father comma
When 8edo is treated as a very inaccurate 5-limit system, it ends up tempering out the Father comma, 16/15. In fact, it is the largest edo that tempers this comma. What this means is that intervals 16/15 apart in 8edo map to the same note, such as 4/3 being mapped to the same note as 5/4.
Some other odd equivalencies include:
0-2-5: which can be seen as a minor triad (10:12:15), a sus2 triad (9:8:12), or a major triad in first inversion (5:6:8).
0-3-5: which can be seen as a major triad (4:5:6), a sus4 triad (6:8:9), or a minor chord in second inversion (15:20:24).
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +48.0 | +63.7 | -68.8 | -53.9 | +48.7 | +59.5 | -38.3 | +45.0 | +2.5 | -20.8 | -28.3 |
| Relative (%) | +32.0 | +42.5 | -45.9 | -35.9 | +32.5 | +39.6 | -25.5 | +30.0 | +1.7 | -13.9 | -18.8 | |
| Steps (reduced) |
13 (5) |
19 (3) |
22 (6) |
25 (1) |
28 (4) |
30 (6) |
31 (7) |
33 (1) |
34 (2) |
35 (3) |
36 (4) | |
Octave shrinking
8edo's approximation of JI can be improved via octave shrinking. Compressing 8edo's octave from 1200 cents down to 1187 cents gives the tuning called 29ed12.
Of all prime harmonics up to 31, pure-octave 8edo only manages to approximate 2/1 and 19/1 within 15 cents, completely missing all the others.
By contrast, 29ed12 approximates 2/1, 11/1, 13/1, 17/1 and 31/1 all within 15 cents.
Of all integer harmonics up to 30, pure-octave 8edo approximates the following within 20 cents:
- 2, 4, 8, 16, 19, 27.
Of all integer harmonics up to 30, 29ed12 approximates the following within 20 cents:
- 2, 6, 11, 12, 13, 17, 20, 22, 25, 26.
This provides 29ed12 with a comparatively larger, more diverse palette of consonances than pure-octaves 8edo.
The nearest zeta peak index tunings to 8edo don't have an interval within 20 cents of 2/1, making them unrecognisable as stretched or compressed 8edo but instead more like entirely new scales in their own right.
Subsets and supersets
8edo contains 2edo and 4edo as subsets. Among its supersets are 16edo, 24edo, 32edo, ….
Intervals
| Steps | Cents | JI approximation | Other | ||
|---|---|---|---|---|---|
| 2.11/3.13/5.19* | 2.5/3.11/3.13/5* | 10:11:12:13:14* | Patent val ⟨8 13 19] | ||
| 0 | 0 | 1/1 | 1/1 | 1/1 | 1/1, 16/15 |
| 1 | 150 | 12/11 | 12/11 | 12/11, 11/10 | 10/9, 25/24 |
| 2 | 300 | 19/16 | 6/5 | 6/5 | 6/5, 9/8 |
| 3 | 450 | 13/10 | 13/10 | 13/10 | 4/3, 5/4 |
| 4 | 600 | 7/5, 10/7 | 27/20, 25/18, 36/25 | ||
| 5 | 750 | 20/13 | 20/13 | 20/13 | 3/2, 8/5 |
| 6 | 900 | 32/19 | 5/3 | 5/3 | 5/3, 16/9 |
| 7 | 1050 | 11/6 | 11/6 | 20/11, 11/6 | 9/5, 48/50 |
| 8 | 1200 | 2/1 | 2/1 | 2/1 | 2/1, 15/8 |
* Allows inversion by 2/1; other interpretations also possible
Notation
Ups and downs notation
8edo can be notated as a subset of 24edo, using ups and downs. It can also be notated as a subset of 16edo, but this is a less intuitive notation.
| Edostep | Cents | 24edo subset notation (EUs: vvA1 and d2) |
16edo subset notation (major narrower than minor) |
16edo subset notation (major wider than minor) |
3L 2s notation (J = 1/1) |
Audio | |||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0¢ | P1 | D | P1 | D | P1 | D | J | |
| 1 | 150 | ~2 | vE | M2 | E | m2 | E | K | |
| 2 | 300 | m3 | F | M3 | F# | m3 | Fb | K#, Lb | |
| 3 | 450 | ^M3 / v4 | ^F# / vG | d3 / A4 | Fb / G# | A3, D4 | F#, Gb | L | |
| 4 | 600 | A4, d5 | G#, Ab | d4, A5 | Gb, A# | A4, D5 | G#, Ab | M | |
| 5 | 750 | ^5, vm6 | ^A, vBb | d5, A6 | Ab, B# | A5, d6 | A#, Bb | M#, Nb | |
| 6 | 900 | M6 | B | m6 | Bb | M6 | B# | N | |
| 7 | 1050 | ~7 | ^C | m7 | C | M7 | C | N#, Jb | |
| 8 | 1200 | P8 | D | P8 | D | P8 | D | J | |
This is a heptatonic notation generated by 5ths (5th meaning 3/2). Alternative notations include pentatonic 5th-generated, octatonic, and heptatonic 2nd-generated.
Pentatonic 5th-generated: D * E G * A C * D (generator = 5\8 = perfect 5thoid)
D - D#/Eb - E - G - G#/Ab - A - C - C#/Db - D
P1 - A1/ms3 - Ms3 - P4d - A4d/d5d - P5d - ms7 - Ms7/d8d - P8d (s = sub-, d = -oid, see 5edo notation)
pentatonic genchain of 5ths: ...Cb - Gb - Db - Ab - Eb - C - G - D - A - E - C# - G# - D# - A# - E#...
pentatonic genchain of 5ths: ...d8d - d5d - ms3 - ms7 - P4d - P1 - P5d - Ms3 - Ms7 - A4d - A1... (s = sub-, d = -oid)
Enharmonic unison: ds3
Octatonic: A B C D E F G H A (every interval is a generator)
P1 - P2 - P3 - P4 - P5 - P6 - P7 - P8 - P9
Enharmonic unison: none
Heptatonic 2nd-generated: D E F G * A B C D (generator = 1\8 = perfect 2nd = 150¢)
D - E - F - G - G#/Ab - A -B - C - D
P1 - P2 - m3 - M3/m4 - M4/m5 - M5/m6 - M6 - P7 - P8
genchain of 2nds: ...D# - E# - F# - G# - A - B - C - D - E - F - G - Ab - Bb - Cb - Db...
genchain of 2nds: ...A1 - A2 - M3 - M4 - M5 - M6 - P7 - P1 - P2 - m3 - m4 - m5 - m6 - d7 - d8...
Enharmonic unison: d2
Sagittal notation
This notation is a subset of the notations for EDOs 24, 48, and 72.
Evo flavor

Revo flavor

Evo-SZ flavor

Because it contains no Sagittal symbols, this Evo-SZ Sagittal notation is also a Stein-Zimmerman notation.
Chord names
Ups and downs can name any 8edo chord. Alterations are always enclosed in parentheses, additions never are. An up, down or mid immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13).
8edo chords are very ambiguous, with many chord homonyms. Even the major and minor triads are homonyms. Chord components usually default to M2, M3, P4, P5, M6, m7, M9, P11 and M13. Thus D7 has a M3, P5 and m7. 8-edo chord names using 24edo subset names are greatly simplified by using different defaults: instead of the conventional M2, M3, P4, P5, M6, m7, M9, P11 and M13, we have ~2, ^M3, v4, ^5, M6, ~7, ~9, v11 and M13. Thus D7 becomes ^M3, ^5 and ~7.
| Chord edosteps | Chord notes | Full name | Abbreviated name | Homonyms |
|---|---|---|---|---|
| 0 – 3 – 5 | D ^F♯ ^A | D^(^5) | D | ^F♯m or vGm |
| 0 – 2 – 5 | D F ^A | Dm(^5) | Dm | ^A or vB♭ |
| 0 – 3 – 5 – 7 | D ^F♯ ^A ^C | D^7(^5) | D7 | ^F♯m♯11 or vGm♯11 |
| 0 – 3 – 5 – 6 | D ^F♯ ^A B | D6(^3,^5) | D6 | Bm7 and vG,♯9 |
| 0 – 2 – 5 – 7 | D F ^A ^C | Dm,~7(^5) | Dm7 | F6 and vB♭,♯9 |
| 0 – 2 – 5 – 6 | D F ^A B | Dm6(^5) | Dm6 | Bm7(♭5) |
| 0 – 2 – 4 – 7 | D F A♭ ^C | Ddim,~7 | Dm7(♭5) | Fm6 |
Approximation to JI
Regular temperament properties
Uniform maps
| Min. size | Max. size | Wart notation | Map |
|---|---|---|---|
| 7.7018 | 7.8866 | 8bcef | ⟨8 12 18 22 27 29] |
| 7.8866 | 7.9493 | 8cef | ⟨8 13 18 22 27 29] |
| 7.9493 | 7.9675 | 8cf | ⟨8 13 18 22 28 29] |
| 7.9675 | 7.9720 | 8f | ⟨8 13 19 22 28 29] |
| 7.9720 | 8.0147 | 8 | ⟨8 13 19 22 28 30] |
| 8.0147 | 8.2383 | 8d | ⟨8 13 19 23 28 30] |
Commas
8et tempers out the following commas. This assumes val ⟨8 13 19 22 28 30].
| Prime limit |
Ratio[1] | Monzo | Cents | Color name | Name(s) |
|---|---|---|---|---|---|
| 3 | 8192/6561 | [13 -8⟩ | 384.35 | sawa 4th | Pythagorean diminished fourth |
| 5 | 16/15 | [4 -1 -1⟩ | 111.73 | gu 2nd | Father comma, classic limma |
| 5 | 648/625 | [3 4 -4⟩ | 62.57 | Quadgu | Diminished comma, major diesis |
| 5 | 250/243 | [1 -5 3⟩ | 49.17 | Triyo | Porcupine comma, maximal diesis |
| 5 | 78732/78125 | [2 9 -7⟩ | 13.40 | Sepgu | Sensipent comma, medium semicomma |
| 7 | 64/63 | [6 -2 0 -1⟩ | 27.26 | Ru | Septimal comma, Archytas' comma, Leipziger Komma |
| 7 | 875/864 | [-5 -3 3 1⟩ | 21.90 | Zotriyo | Keema |
| 7 | (12 digits) | [-9 8 -4 2⟩ | 8.04 | Labizogugu | Varunisma |
| 7 | 6144/6125 | [11 1 -3 -2⟩ | 5.36 | Sarurutrigu | Porwell comma |
| 11 | 100/99 | [2 -2 2 0 -1⟩ | 17.40 | Luyoyo | Ptolemisma |
| 11 | 121/120 | [-3 -1 -1 0 2⟩ | 14.37 | Lologu | Biyatisma |
| 11 | 176/175 | [4 0 -2 -1 1⟩ | 9.86 | Lorugugu | Valinorsma |
| 11 | 65536/65219 | [16 0 0 -2 -3⟩ | 8.39 | Satrilu-aruru | Orgonisma |
| 11 | 385/384 | [-7 -1 1 1 1⟩ | 4.50 | Lozoyo | Keenanisma |
| 11 | 4000/3993 | [5 -1 3 0 -3⟩ | 3.03 | Triluyo | Wizardharry comma |
| 13 | 40/39 | [3 -1 1 0 0 -1⟩ | 43.83 | Thuyo unison | Tridecimal minor diesis |
- ↑ Ratios longer than 10 digits are presented by placeholders with informative hints
Scales
Scala file
Here is a .scl file of 8edo: 08-edo.scl
! 08-EDO.scl ! 8 EDO 8 ! 150.00 300.00 450.00 600.00 750.00 900.00 1050.00 2/1
Temperaments
8edo is fairly composite, so the only step that generates a mos scale that covers every interval other than the 1 is the 3, producing scales of 332 and 21212. In terms of temperaments, in the 5-limit this is best interpreted as father, as 8edo is the highest edo that tempers out the diatonic semitone in it's patent val, merging 5/4 and 4/3 into a single interval, which is also the generator. This means major and minor chords are rotations of each other, making them inaccurate but very simple, with even the 5 note mos having 3 of both and providing a functional skeleton of 5-limit harmony, albeit with some very strange enharmonic equivalences. In terms of 7-limit extensions things get even more inaccurate, as the patent val supports mother, but the ideal tuning for that is much closer to 5edo. The 8d val supports septimal father and pater, and is much closer to the ideal tuning for both, as the extremely sharp 7 works better with the 3 & 5. In terms of multi-period temperaments, it makes for a near perfect walid or a much less accurate diminished scale.
Instruments
A Lumatone mapping for 8edo is available.
Music
- mushroom (2024)
- 8edo-pre-improv (2011)
- darkreflections(sketch) (2011)
- skiphop(sketch) (2011)
- octo-icy-pensive(sketch), octo-icy-pensive-echo(sketch) (2011)
- "Malebolge", from Transcendissonance (2011)
- Špendlíky (1988-2005)
- Like yamashiro (2021)
- Like Ensor's paintings (2023)
- "Fantasia & Fugue a4 in 8ET", from The Equal-Tempered Keyboard (1999-2022)
- "Disorient", from Edolian (2020)
- Towards Dissolution (2020)
- Octahedron (2024)
- Reckoner (2025)
- News To Me (2011)
- Tomorrow Night (pop music from 2045) (2011)
- "7. 8 / octave", from Comets Over Flatland (2007)
- Jonky Jazz (2025)
Ear training
8edo ear-training exercises by Alex Ness available here.
See also
- Octatonic scale - a scale based on alternating whole and half steps
- Fendo family - temperaments closely related to 8edo