18edo

← 17edo

18edo

19edo →

Prime factorization

2 × 3²

Step size

66.6667 ¢

Fifth

11\18 (733.333 ¢)

Semitones (A1:m2)

5:-1 (333.3 ¢ : -66.67 ¢)

Dual sharp fifth

11\18 (733.333 ¢)

Dual flat fifth

10\18 (666.667 ¢) (→ 5\9)

Dual major 2nd

3\18 (200 ¢) (→ 1\6)

Consistency limit

7

Distinct consistency limit

5

18 equal divisions of the octave (abbreviated 18edo or 18ed2), also called 18-tone equal temperament (18tet) or 18 equal temperament (18et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 18 equal parts of about 66.7 ¢ each. Each step represents a frequency ratio of 2^1/18, or the 18th root of 2.

18edo is also known as the third-tone system.

Theory

18edo does not include the 3rd or 7th harmonics, and contains the same controversial tuning of 5/4 as 12edo does. It does, however, render more accurate tunings of 7/6, 21/16, 15/11, 12/7, and 13/7. It is also the smallest edo to approximate the harmonic series chord 5:6:7 without tempering out 36/35 (and thus without using the same interval to approximate both 6/5 and 7/6).

In order to access the excellent consonances actually available, one must take a considerably "non-common-practice" approach, meaning to avoid the usual closed-voice "root-3rd-5th" type of chord and instead use chords which are either more compressed or more stretched out. 18edo may be treated as a temperament of the 17-limit 4*18 subgroup just intonation subgroup 2.9.75.21.55.39.51. On this subgroup it tempers out exactly the same commas as 72edo does on the full 17-limit, and gives precisely the same tunings. The subgroup can be put into a single chord, for example 32:36:39:42:51:55:64:75 (in terms of 18edo, 0-3-5-7-12-14-18-22), and transpositions and inversions of this chord or its subchords provide plenty of harmonic resources. 18edo also approximates 12:13:14:17:23:27:29 quite well, with the least maximum relative error out of any edos ≤ 100 (the worst-approximated interval is 23/13, with relative error 18.36%). Hence it can be viewed as an "/3 temperament" (/3 used in the primodality sense), specifically in the 2.9.13/12.7/6.17/12.23/12.29/24 subgroup. As for more simple subgroups, 18edo can be treated as a 2.9.5.7 subgroup temperament.

However, less accurate approximations can be used, and 18edo can be treated as a 7-limit (with 3s) exotemperament with the mapping ⟨18 29 42 51]. This maps 3/2 to 733.33¢, 5/4 to 400¢ and 7/4 to 1000¢; as a result, 28/27 is tempered out, and weird things happen: 9/8 and 7/6 are both mapped to 266.67¢, while 8/7 gets mapped below both of them to 200¢, making for a rather disordered 7-odd-limit tonality diamond, but hey, whatever floats your boat! This 7-limit mapping supports 7-limit sixix thus is strongly associated with 18edo's 4L 3s mos.

18edo contains sub-edos 2, 3, 6, and 9, and itself is half of 36edo and one-fourth of 72edo. It bears some similarities to 13edo (with its very flat 4ths and nice subminor 3rds), 11edo (with its very sharp minor 3rds, two of which span a very flat 5th), 16edo (with its sharp 4ths and flat 5ths), and 17edo and 19edo (with its narrow semitone, three of which comprise a whole-tone). It is an excellent tuning for those seeking a forceful deviation from the common practice.

18edo is the basic example of a dual-fifth system (beyond perhaps 11 or 13edo), as the sharp and flat fifths multiply to a good approximation of 9/4. By alternating these fifths, a diatonic scale (5L 1m 1s) is generated which is similar to 19edo's diatonic, but cut short by one step.

Odd harmonics

Approximation of odd harmonics in 18edo
Harmonic		3	5	7	9	11	13	15	17	19	21	23
Error	Absolute (¢)	+31.4	+13.7	+31.2	-3.9	-18.0	+26.1	-21.6	+28.4	-30.8	-4.1	-28.3
Error	Relative (%)	+47.1	+20.5	+46.8	-5.9	-27.0	+39.2	-32.4	+42.6	-46.3	-6.2	-42.4
Steps (reduced)		29 (11)	42 (6)	51 (15)	57 (3)	62 (8)	67 (13)	70 (16)	74 (2)	76 (4)	79 (7)	81 (9)

Notation

Ups and downs notation

18edo can be notated with ups and downs. The notational 5th is the 2nd-best approximation of 3/2, 10\18. This is only 4¢ worse that the best approximation, which becomes the up-fifth. This tuning can be notated with conventional notation, including the staff, note names, relative notation, etc. in two ways.

The first and most common defines sharp/flat, major/minor and aug/dim in terms of the native antidiatonic scale, such that sharp is higher pitched than flat, and major/aug is wider than minor/dim, as would be expected. Because it does not follow diatonic conventions, conventional interval arithmetic no longer works, e.g. M2 + M2 isn't M3, and D + M2 isn't E. Because antidiatonic is the sister scale to diatonic, you can solve this by swapping major and minor in interval arithmetic rules. Note that the notes that form chords are different from in diatonic: for example, a major chord, P1 – M3 – P5, is approximately 4:5:6 as would be expected, but is notated C-E#-G on C.

Alternatively, one can essentially pretend the native antidiatonic scale is a normal diatonic, meaning that sharp is lower in pitch than flat (since the "S" step is larger than the "L" step) and major/aug is narrower than minor/dim. The primary purpose of doing this is to allow music notated in 12edo or another diatonic system to be directly translated "on the fly" (or to allow support for this tuning in tools that only allow chain-of-fifths notation), and it carries over the way interval arithmetic works from diatonic notation, at the cost of notating the sizes of intervals and the shapes of chords incorrectly: that is, a major chord, P1-M3-P5, is notated C-E-G on C, but is no longer ~4:5:6 (since the third is closer to a minor third).

For the sake of clarity, the first notation is commonly called "melodic notation", and the second is called "harmonic notation", but this is a bit of a misnomer as both preserve different features of the notation of harmony.

Comparison of notations
	P1-M3-P5 ~ 4-5-6	P1-M3-P5 = C-E-G on C
Diatonic notation	No	Yes
Antidiatonic notation	Yes	No

Degree	Cents	Up/down notation using the narrow 5th of 10\18, with major wider than minor			Up/down notation using the narrow 5th of 10\18, with major narrower than minor			5L3s Notation
0	0	perfect unison	P1	D	perfect unison	P1	D	C
1	67	up unison, downminor 2nd	^1, vm2	^D, vE	up unison, downmajor 2nd	^1, vM2	^D, vE	Db
2	133	minor 2nd	m2	E	major 2nd	M2	E	C#
3	200	mid 2nd	~2	^E	mid 2nd	~2	^E	D
4	267	major 2nd, minor 3rd	M2, m3	E#, Fb	minor 2nd, major 3rd	m2, M3	Eb, F#	Eb
5	333	mid 3rd	~3	vF	mid 3rd	~3	vF	D#
6	400	major 3rd	M3	F	minor 3rd	m3	F	E
7	467	upmajor 3rd, down 4th	^M3, v4	^F, vG	upminor 3rd, down 4th	^m3, v4	^F, vG	F
8	533	perfect 4th	P4	G	perfect 4th	P4	G	Gb
9	600	up 4th, down 5th	^4, v5	^G, vA	up 4th, down 5th	^4, v5	^G, vA	F#
10	667	perfect 5th	P5	A	perfect 5th	P5	A	G
11	733	up 5th, downminor 6th	^5, vm6	^A, vB	up fifth, downmajor 6th	^5, vM6	^A, vB	Hb
12	800	minor 6th	m6	B	major 6th	M6	B	G#
13	867	mid 6th	~6	^B	mid 6th	~6	^B	H
14	933	major 6th, minor 7th	M6, m7	B#, Cb	minor 6th, major 7th	m6, M7	Bb, C#	A
15	1000	mid 7th	~7	vC	mid 7th	~7	vC	Bb
16	1067	major 7th	M7	C	minor 7th	m7	C	A#
17	1133	upmajor 7th, down 8ve	^M7, v8	^C, vD	upminor 7th, down 8ve	^m7, v8	^C, vD	B
18	1200	perfect 8ve	P8	D	perfect 8ve	P8	D	C

This is a heptatonic notation generated by 5ths (5th meaning 3/2). Alternative notations include pentatonic 5th-generated, nonotonic 5th-generated, and heptatonic 3rd-generated.

Pentatonic 5th-generated: D * * * E * * G * * * A * * C * * * D (generator = wide 3/2 = 11\18 = perfect 5thoid)

D - D# - Dx/Ebb - Eb - E - E# - Gb - G - G# - Gx/Abb - Ab - A - A# - Cb - C - C# - Cx/Dbb - Db - D

P1 - A1 - ds3 - ms3 - Ms3 - As3 - d4d - P4d - A4d - AA4d/dd5d - d5d - P5d - A5d - ds7 - ms7 - Ms7 - As7 - d8d - P8d (s = sub-, d = -oid)

pentatonic genchain of fifths: ...Ebb - Cb - Gb - Db - Ab - Eb - C - G - D - A - E - C# - G# - D# - A# - E# - Cx...

pentatonic genchain of fifths: ...ds3 - ds7 - d4d - d8d - d5d - ms3 - ms7 - P4d - P1 - P5d - Ms3 - Ms7 - A4d - A1 - A5d - As3 - As7... (s = sub-, d = -oid)

Nonatonic 5th-generated: A * B * C * D * E * F * G * H * J * A (every other note is a generator, all notes are perfect)

1 - ^1/v2 - 2 - ^2/v3 - 3 - ^3/v4- 4 - ^4/v5 - 5 - ^5/v6 - 6 - ^6/v7 - 7 - ^7/v8 - 8 - ^8/v9 - 9 - ^9/v10 - 10

heptatonic 3rd-generated: D * * E * F * * G * A * * B * C * * D (generator = 5\18 = perfect 3rd)

D - D# - Eb - E - E#/Fb - F - F# - Gb - G - G#/Ab - A - A# - Bb - B - B#/Cb - C - C# - Db - D

P1 - A1/d2 - m2 - M2 - A2/d3 - P3 - A3/d4 - m4 - M4 - A4/d5 - m5 - M5 - A5/d6 - P6 - A6/d7 - m7 - M7 - A7/d8 - P8

genchain of thirds: ...E# - G# - B# - D# - F# - A# - C# - E - G - B - D - F - A - C - Eb - Gb - Bb - Db - Fb - Ab - Cb... ("Every good boy deserves fudge and candy")

genchain of thirds: ...A4 - A6 - A1 - A3 - M5 - M7 - M2 - M4 - P6 - P1 - P3 - m5 - m7 - m2 - m4 - d6 - d8 - d3 - d5...

Sagittal notation

This notation is a subset of the notations for EDOs 36 and 72 and a superset of the notation for 6-EDO.

Evo flavor

Revo flavor

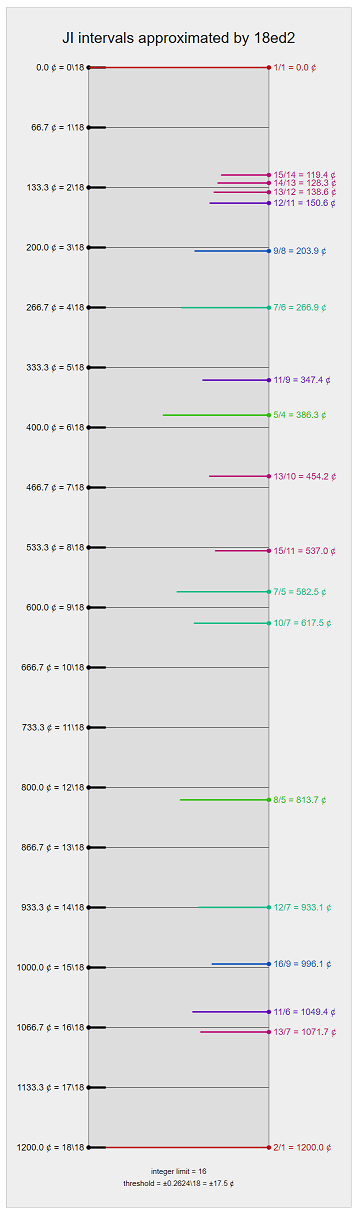
Representations of JI intervals

Degree	Cents	Nearest Ratio	Error	17-Limit Ratios ^[1]
0	0.000	1/1	0	1/1
1	66.667	27/26	+1.329	78/75, 75/72
2	133.333	27/25	+0.096	51/55, 42/39
3	200.000	9/8	-3.910	9/8
4	266.667	7/6	-0.204	75/64
5	333.333	17/14 or 40/33	-2.796 +0.293	39/32
6	400.000	5/4 or 44/35	+13.686 +3.822	64/55
7	466.667	21/16	-4.114	21/16
8	533.333	15/11	-3.617	102/75
9	600.000	17/12 or 24/17	-3.000 +3.000	17/12
10	666.667	22/15	+3.617	75/51
11	733.333	32/21	+4.114	32/21
12	800.000	8/5 or 35/22	-13.686 -3.822	51/32
13	866.667	28/17 or 33/20	+2.796 -0.293	64/39
14	933.333	12/7	+0.204	55/32
15	1000.000	16/9	+3.910	16/9
16	1066.667	50/27	-0.096	39/21
17	1133.333	52/27	-1.329	75/39
18	1200.000	2/1	0	2/1**

↑ based on the above description of 18-EDO as a 2.9.75.21.55.39.51 subgroup temperament

Regular temperament properties

Uniform maps

13-limit uniform maps between 17.8 and 18.2
Min. size	Max. size	Wart notation	Map
17.7775	17.8731	18bcdf	⟨18 28 41 50 62 66]
17.8731	17.9708	18bdf	⟨18 28 42 50 62 66]
17.9708	17.9815	18bd	⟨18 28 42 50 62 67]
17.9815	17.9885	18d	⟨18 29 42 50 62 67]
17.9885	18.0666	18	⟨18 29 42 51 62 67]
18.0666	18.2411	18e	⟨18 29 42 51 63 67]

Commas

18et tempers out the following commas. (Note: This assumes the val ⟨18 29 42 51 62 67].)

Prime limit	Ratio^[1]	Monzo	Cents	Color name	Name(s)
3	(18 digits)	[29 -18⟩	564.81	Wa-18	18-comma
5	128/125	[7 0 -3⟩	41.06	Trigu	Augmented comma, diesis
5	(20 digits)	[23 6 -14⟩	3.34	Sasa-sepbigu	Vishnuzma, Semisuper comma
7	50/49	[1 0 2 -2⟩	34.98	Biruyo	Jubilisma, tritonic diesis
7	686/675	[1 -3 -2 3⟩	27.99	Trizo-agugu	Senga
7	875/864	[-5 -3 3 1⟩	21.90	Zotriyo	Keema
7	1728/1715	[6 3 -1 -3⟩	13.07	Triru-agu	Orwellisma
7	16875/16807	[0 3 4 -5⟩	6.99	Quinru-aquadyo	Mirkwai comma
7	3136/3125	[6 0 -5 2⟩	6.08	Zozoquingu	Hemimean comma
11	99/98	[-1 2 0 -2 1⟩	17.58	Loruru	Mothwellsma
11	100/99	[2 -2 2 0 -1⟩	17.40	Luyoyo	Ptolemisma
11	65536/65219	[16 0 0 -2 -3⟩	8.39	Satrilu-aruru	Orgonisma
11	385/384	[-7 -1 1 1 1⟩	4.50	Lozoyo	Keenanisma
11	9801/9800	[-3 4 -2 -2 2⟩	0.18	Bilorugu	Kalisma
13	91/90	[-1 -2 -1 1 0 1⟩	19.13	Thozogu	Superleap comma, biome comma

↑ Ratios longer than 10 digits are presented by placeholders with informative hints

Scales

Note: This list excludes scales found in 9edo.

Pentatonic

3L 2s: 4 4 3 4 3

Hexatonic

4L 2s: 4 4 1 4 4 1

2L 4s: 2 5 2 2 5 2

Heptatonic

4L 3s: 3 2 3 2 3 3 2

Octatonic

5L 3s: 3 1 3 3 1 3 3 1

2L 6s: 2 2 3 2 2 2 3 2

Enneatonic

3L 6s: 4 1 1 4 1 1 4 1 1

Decatonic

8L 2s: 2 2 1 2 2 2 2 1 2 2

Hendecatonic

7L 4s: 2 1 2 2 1 2 2 1 2 1 2

Dodecatonic

3L 9s: 3 1 1 1 3 1 1 1 3 1 1 1

6L 6s: 2 1 2 1 2 1 2 1 2 1 2 1

Pentadecatonic

3L 12s: 2 1 1 1 1 2 1 1 1 1 2 1 1 1 1

Application to guitar

18edo is an ideal scale for the first-time refretter, because you can retain all the even-number frets from 12-tET--essentially 1/3 of your work is done for you!

The 8-note oneirotonic scale maps very simply to a 6-string guitar tuned in "reverse-standard" tuning (tune using four 466.667¢ intervals, with one 533.333¢ interval between the 2nd and 3rd strings), making for a softer learning-curve than EDOs like 14, 16, or 21 (all of which are most evenly open-tuned using a series of sharpened 4ths and a minor or neutral 3rd, and whose scales thus often require position-shifting and/or larger stretches of the hand).