159edo/Notation
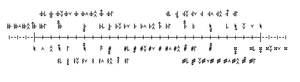
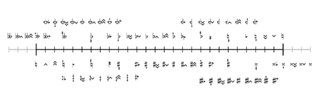
Helmholtz–Ellis-based notation
The first 159edo-notation system proposed by Aura modifies the Helmholtz–Ellis notation in such a way that undecimal quartertones play a central role alongside the traditional accidentals, with mainstream quartertone accidentals being used to represent them. This is because undecimal quartertones are actually useful in modulation to keys that are not on the same circle of fifths while being simultaneously within an unnoticeable comma's distance from the quartertone of 24edo, which many musicians outside the microtonal community proper have at least a passing familiarity with. It should be noted that most of the symbols listed in this section derive their functions from JI. In addition, it should be noted that accidentals are not just modifiers for single notes, but signs that indicate the change of both the tonal and modal base, and can thus appear in key signatures.
Available base glyphs
Quartertones and syntonic commas
As in HEJI, classic accidentals and arrows for syntonic commas are combined. Beyond HEJI, quartertone accidentals are also used, being combined with syntonic comma arrows in the same way.
| −30 | −22 | −15 | −7 | 0 | +7 | +15 | +22 | +30 | |
|---|---|---|---|---|---|---|---|---|---|
| +6 | |||||||||
| +3 | |||||||||
| 0 | |||||||||
| −3 | |||||||||
| −6 |
Septimal commas and darts
Glyphs for septimal commas and darts are also used, but are generally not combined with each other except in certain musical contexts such as modulation. That said, if this system were to be extended to the 13-limit, the septimal comma glyphs would likely be combined with the 13-limit glyphs due to both 7-limit and 13-limit intervals having close connections to trientones (one third tones).
The septimal comma glyph traditionally indicates a change by 64/63, and thus, in this particular system, it is bound to the equivalent step size, which is around 30 cents- slightly larger than normal.
| Delta | Glyph |
|---|---|
| +8 | |
| +4 | |
| −4 | |
| −8 |
The dart glyph in this system indicates a change by a single 159edo step (around 7.5 cents). As the dart has no traditional binding to a specific comma, it can also be used for other EDOs to indicate a single step in their corresponding notation systems.
| Delta | Glyph |
|---|---|
| +2 | |
| +1 | |
| −1 | |
| −2 |
Combined accidentals
The following table illustrates modification of a given tone by accidentals up to 30 steps of 159edo. The terms in the glyph name sections reflect absolute displacements, – means down, + means up. Furthermore, symbols with multiple names will have both names sharing the same cell. The choice between the primary and secondary glyphs for any given step is often determined both by absolute TE error and by harmonic and melodic context for any given score, particularly as the primary and secondary glyphs usually reflect different intervals in Just Intonation. For reference, the just whole tone interval, 9/8, is mapped to 27 steps of 159 edo (or 9 steps of 53edo) which is (27*1200/159=) 203.77 cents (0.2 cents flat).
| Delta | Primary Glyph | Primary Glyph Name | Secondary Glyph | Secondary Glyph Name | Remarks |
|---|---|---|---|---|---|
| 0 | Natural | ||||
| −1 | Dart down | This is nothing more than a better version of the v marking from Ups and downs notation.
| |||
| +1 | Dart up | This is nothing more than a better version of the ^ marking from Ups and downs notation.
| |||
| −2 | Double dart down | This is two darts down fused into a single glyph for a more compact representation of vv from Ups and downs notation.
| |||
| +2 | Double dart up | This is two darts up fused into a single glyph for a more compact representation of ^^ from Ups and downs notation.
| |||
| −3 | Natural –Syntonic comma | Quarter flat +Septimal comma, Demiflat +Septimal comma | The intervals represented by the primary and secondary glyphs for this step differ by 385/384 in Just Intonation. | ||
| +3 | Natural +Syntonic comma | Quarter sharp –Septimal comma, Demisharp –Septimal comma | The intervals represented by the primary and secondary glyphs for this step differ by 385/384 in Just Intonation. | ||
| −4 | Quarter flat +Syntonic comma, Demiflat +Syntonic comma | Septimal comma down | The primary glyph overall represents a lowering by 55/54. | ||
| +4 | Quarter sharp –Syntonic comma, Demisharp –Syntonic comma | Septimal comma up | The primary glyph overall represents a raising by 55/54. | ||
| −5 | Quarter flat with double dart up, Demiflat with double dart up | ||||
| +5 | Quarter sharp with double dart down, Demisharp with double dart down | ||||
| −6 | Quarter flat with dart up, Demiflat with dart up | Natural –2 Syntonic commas | |||
| +6 | Quarter sharp with dart down, Demisharp with dart down | Natural +2 Syntonic commas | |||
| −7 | Quarter flat, Demiflat | This glyph represents a lowering by 33/32, much like its identical Helmholtz-Ellis equivalent. | |||
| +7 | Quarter sharp, Demisharp | This glyph represents a raising by 33/32, replacing its Helmholtz-Ellis equivalent on account of familiarity. | |||
| −8 | Quarter flat, Demiflat with Dart down | 2 Septimal commas down | |||
| +8 | Quarter sharp, Demisharp with Dart up | 2 Septimal commas up | |||
| −9 | Quarter flat with double dart down, Demiflat with double dart down | Flat +2 Syntonic commas | |||
| +9 | Quarter sharp with double dart up, Demisharp with double dart up | Sharp –2 Syntonic commas | |||
| −10 | Quarter flat –Syntonic comma, Demiflat –Syntonic comma | ||||
| +10 | Quarter sharp +Syntonic comma, Demisharp +Syntonic comma | ||||
| −11 | Quarter flat –Septimal comma, Demiflat –Septimal comma | Flat +Septimal comma | The primary glyph overall represents a lowering by 22/21, and is the more simple of the two options presented here. | ||
| +11 | Quarter sharp +Septimal comma, Demisharp +Septimal comma | Sharp –Septimal comma | The primary glyph overall represents a raising by 22/21, and is the more simple of the two options presented here. | ||
| −12 | Flat +Syntonic comma | ||||
| +12 | Sharp –Syntonic comma | ||||
| −13 | Flat with double dart up | ||||
| +13 | Sharp with double dart down | ||||
| −14 | Flat with dart up | ||||
| +14 | Sharp with dart down | ||||
| −15 | Flat | As this glyph represents a lowering by an apotome, and as the apotome is a complicated interval, this glyph is generally more likely to be seen as part of a key signature than as an accidental when not combined with other glyphs. | |||
| +15 | Sharp | As this glyph represents a raising by an apotome, and as the apotome is a complicated interval, this glyph is generally more likely to be seen as part of a key signature than as an accidental when not combined with other glyphs. | |||
| −16 | Flat with dart down | ||||
| +16 | Sharp with dart up | ||||
| −17 | Flat with double dart down | ||||
| +17 | Sharp with double dart up | ||||
| −18 | Flat –Syntonic comma | Three quarter flat +Septimal comma, Sesquiflat +Septimal comma | If accidentals for the 13-limit are added to this system, this will be a prime spot for one of them. | ||
| +18 | Sharp +Syntonic comma | Three quarter sharp –Septimal comma, Sesquisharp –Septimal comma | If accidentals for the 13-limit are added to this system, this will be a prime spot for one of them. | ||
| −19 | Three quarter flat +Syntonic comma, Sesquiflat +Syntonic comma | Flat –Septimal comma | The secondary glyph represents a lowering by 243/224, and is the more simple of the two options presented here. | ||
| +19 | Three quarter sharp –Syntonic comma, Sesquisharp –Syntonic comma | Sharp +Septimal comma | The secondary glyph represents a raising by 243/224, and is the more simple of the two options presented here. | ||
| −20 | Three quarter flat with double dart up, Sesquiflat with double dart up | ||||
| +20 | Three quarter sharp with double dart down, Sesquisharp with double dart down | ||||
| −21 | Three quarter flat with dart up, Sesquiflat with dart up | Flat –2 Syntonic commas | |||
| +21 | Three quarter sharp with dart down, Sesquisharp with dart down | Sharp +2 Syntonic commas | |||
| −22 | Three quarter flat, Sesquiflat | This glyph represents a lowering by a complex interval comprised of an apotome and a 33/32 quartertone, and as such, is generally more likely to be seen as part of a key signature than as an accidental when not combined with other glyphs. | |||
| +22 | Three quarter sharp, Sesquisharp | This glyph represents a raising by a complex interval comprised of an apotome and a 33/32 quartertone, and as such, is generally more likely to be seen as part of a key signature than as an accidental when not combined with other glyphs. | |||
| −23 | Three quarter flat with dart down, Sesquiflat with dart down | ||||
| +23 | Three quarter sharp with dart up, Sesquisharp with dart up | ||||
| −24 | Three quarter flat with double dart down, Sesquiflat with double dart down | Double flat +2 Syntonic commas | |||
| +24 | Three quarter sharp with double dart up, Sesquisharp with double dart up | Double sharp –2 Syntonic commas | |||
| −25 | Three quarter flat –Syntonic comma, Sesquiflat –Syntonic comma | ||||
| +25 | Three quarter sharp +Syntonic comma, Sesquisharp +Syntonic comma | ||||
| −26 | Three quarter flat –Septimal comma, Sesquiflat –Septimal comma | Double flat +Septimal comma | |||
| +26 | Three quarter sharp +Septimal comma, Sesquisharp +Septimal comma | Double sharp –Septimal comma | |||
| −27 | Double flat +Syntonic comma | ||||
| +27 | Double sharp –Syntonic comma | ||||
| −28 | Double flat with with double dart up | ||||
| +28 | Double sharp with double dart down | ||||
| −29 | Double flat with dart up | ||||
| +29 | Double sharp with dart down | ||||
| −30 | Double flat | This glyph represents a lowering by a stack of two apotomes, and as such, this glyph is more likely to be seen when combined with other glyphs, and key signatures using this glyph are likely to be considered remote and or exotic. | |||
| +30 | Double sharp | This glyph represents a raising by a stack of two apotomes, and as such, this glyph is more likely to be seen when combined with other glyphs, and key signatures using this glyph are likely to be considered remote and or exotic. |
Advantages and disadvantages
Among the advantages of this system is the fact that it keeps the traditional naturals, sharps, flats, double sharps and double flats, and assigns them to values based on 3-limit JI, resulting in this system having some level of familiarity for musicians from a traditional background. However, the disadvantages of this system are that this system relies on too many glyphs, a number of which need to be deciphered, and furthermore, the arrangement of combined and simple accidentals- as well as arrangement of the quartertone accidentals- is counterintuitive. In addition, a demisharp is approximately a half-sharp, yet here it is called a quarter-sharp, a break with well-established microtonal convention. Finally, two demisharps do not add up to a sharp as one would expect.
Ups-and-downs-based notation
Another system proposed by TallKite uses ups and downs (^ v), with quintuple arrows notated as quip and quid (> <).
- 1\159 = ^ = up
- 2\159 = ^^ = dup
- 3\159 = ^^^ = trup
- 4\159 = v> = quup
- 5\159 = > = quip
- 6\159 = ^> = upquip
- 7\159 = ^^> = dupquip or vvv<# = trudquidsharp
- 8\159 = ^^^> = trupquip or vv<# = dudquidsharp
- 9\159 = v>> = quupquip or v<# = downquidsharp
- 10\159 = <# = quidsharp
- 11\159 = ^<# = quudsharp
- 12\159 = vvv# = trudsharp
- 13\159 = vv# = dudsharp
- 14\159 = v# = downsharp
- 15\159 = # = sharp
Notes flatter than natural can be deduced by symmetry, i.e. C vC vvC vvvC ^<C <C etc. Notes beyond sharp just run through the same list, but adding "sharp": sharp, upsharp, dupsharp, quupsharp, quipsharp... going to double-sharp eventually.
The spectrum of qualities looks like this:
- −6 = v<m = downquidminor (same as upquipmajor of the next lower degree)
- −5 = <m = quidminor
- −4 = ^<m = quudminor
- −3 = vvvm = trudminor
- −2 = vvm = dudminor
- −1 = vm = downminor
- 0 = m = minor
- 1 = ^m = upminor
- 2 = ^^m = dupminor
- 3 = ^^^m = trupminor
- 4 = v>m = quupminor
- 5 = >m = quipminor = <<M = quidquidmajor
- 6 = ^>m = upquipminor = ^<<M = quudquidmajor
- 7 = ^^>m = dupquipminor = vvv<M = trudquidmajor
- 8 = ^^^>m = trupquipminor = vv<M = dudquidmajor
- 9 = v>>m = quudquipminor = v<M = downquidmajor
- 10 = >>m = quipquipminor = <M = quidmajor
- 11= ^<M = quudmajor
- 12 = vvvM = trudmajor
- 13 = vvM = dudmajor
- 14 = vM = downmajor
- 15 = M = major
- 16 = ^M = upmajor
- 17 = ^^M = dupmajor
- 18 = ^^^M = trupmajor
- 19 = v>M = quupmajor
- 20 = >M = quipmajor
- 21 = ^>M = upquipmajor (same as downquidminor of the next higher degree)
Thus 4:5:6:7:9:11 = P1 vvvM3 P5 ^<m7 M9 ^^>11 = C vvvE G ^<Bb D ^^>F = Cvvv9(^<7)^^>11 = C trud-9 quud-7 dupquip-11
Alternatively, drops and lifts can be added to 53edo ups and downs notation to avoid large multiples of ups and downs and to keep the size of an up and a down more consistent with smaller edos.
- 1\159 = / = lift
- 2\159 = \^ = drop-up
- 3\159 = ^ = up
- 4\159 = /^ = lift-up
- 5\159 = \^^ = drop-dup
- 6\159 = ^^ = dup
- 7\159 = /^^ = lift-dup
- 8\159 = \vv# = drop-dudsharp
- 9\159 = vv# = dudsharp
- 10\159 = /vv# = lift-dudsharp
- 11\159 = \v# = drop-downsharp
- 12\159 = v# = downsharp
- 13\159 = /v# = lift-downsharp
- 14\159 = \# = drop-sharp
- 15\159 = # = sharp
The spectrum of qualities for this style looks like this:
- -6 = vvm = dudminor (same as dupmajor of the next lower degree)
- -5 = /vvm = lift-dudminor
- -4 = \vm = drop-downminor
- -3 = vm = downminor
- -2 = /vm = lift-downminor
- -1 = \m = drop-minor
- 0 = m = minor
- 1 = /m = lift-minor
- 2 = \^m = drop-upminor
- 3 = ^m = upminor
- 4 = /^m = lift-upminor
- 5 = \^^m = drop-dupminor = \vvvM = drop-trudmajor
- 6 = ^^m = dupminor = vvvM = trudmajor
- 7 = /^^m = lift-dupminor = /vvvM = lift-trudmajor
- 8 = \^^^m = drop-trupminor = \vvM = drop-dudmajor
- 9 = ^^^m = trupminor = vvM = dudmajor
- 10 = /^^^m = lift-trupminor = /vvM = lift-dudmajor
- 11 = \vM = drop-downmajor
- 12 = vM = downmajor
- 13 = /vM = lift-downmajor
- 14 = \M = drop-major
- 15 = M = major
- 16 = /M = lift-major
- 17 = \^M = drop-upmajor
- 18 = ^M = upmajor
- 19 = /^M = lift-upmajor
- 20 = \^^M = drop-dupmajor
- 21 = ^^M = dupmajor (same as dudminor of the next higher degree)
Advantages and disadvantages
One advantage of this notation is that it keeps the traditional naturals, sharps, flats, double sharps and double flats, and assigns them to values based on 3-limit JI. Thus this notation has some level of familiarity for musicians from a traditional background, while being simpler and more intuitive than the first system. This system avoids half-sharps and half-flats because the sharp and the flat are each 15 edosteps. 15 is an odd number, so there are strictly speaking no half-sharps in 159edo.
Sagittal notation
The following table shows sagittal notation accidentals in one apotome for 159edo.
| Steps | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Accidental |
Advantages and disadvantages
The advantages and disadvantages are largely the same as those of Sagittal notation in general.
Syntonic–rastmic subchroma notation
The second 159edo-notation system proposed by Aura eventually blossomed into syntonic–rastmic subchroma notation, an expansion of neutral circle-of-fifths notation which turns out to be powerful enough to cover systems such as 311edo.
0 natural 1 / rasharp 2 ↑\ raflat synsharp // double rasharp 3 ↑ synsharp 4 ↑/ rasharp synsharp 5 ↑↑\ raflat double synsharp ↑// double rasharp synsharp 6 ↑↑ double synsharp 7 t< artodemisharp 8 t> tendodemisharp 9 #↓↓ double synflat sharp 10 #↓↓/ rasharp double synflat sharp #↓// double rasharp synflat sharp 11 #↓\ raflat synflat sharp 12 #↓ synflat sharp 13 #↓/ rasharp synflat sharp #\\ double raflat sharp 14 #\ raflat sharp 15 # sharp
Advantages and disadvantages
By striking a good balance between the number of accidentals and their semantic consistency, Syntonic-Rastmic Subchroma notation manages to address the weaknesses of both Ups and Downs notation and Sagittal notation, and, as it's derived from Neutral Circle-of-Fifths notation- the de facto standard foundation for notation in 24edo- it is more easily accessible to microtonal musicians at the beginner level, all while retaining Helmholtz-Ellis notation's advantage of fixing the key notation problems that have plagued 53edo itself by means of accounting for the 2.3.5.11 subgroup in general and the syntonic comma specifically.
| View • Talk • EditMusical notation | |
|---|---|
| Universal | Sagittal notation |
| Just intonation | Functional Just System • Ben Johnston's notation (Johnston–Copper notation) • Helmholtz–Ellis notation • Color notation |
| MOS scales | Diamond-mos notation • KISS notation (Quasi-diatonic MOS notation) |
| Temperaments | Circle-of-fifths notation • Ups and downs notation (alternative symbols) • Syntonic–rastmic subchroma notation • Extended meantone notation • Fractional sharp notation |
See musical notation for a longer list of systems by category. See Category:Notation for the most complete, comprehensive list, but not sorted by category. | |