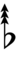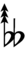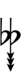61edo
| ← 60edo | 61edo | 62edo → |
Theory
As an equal temperament, 61et is characterized by tempering out 20000/19683 (tetracot comma) and 262144/253125 (passion comma) in the 5-limit. In the 7-limit, the patent val ⟨61 97 142 171] supports valentine (15 & 46), and is the optimal patent val for freivald (24 & 37) in the 7-, 11- and 13-limit. The 61d val ⟨61 97 142 172] is a great tuning for modus and quasisuper, and is a simple but out-of-tune edo tuning for parakleismic. Peter Kosmorsky has an interesting poem about its tuning profile, as follows.
Introductory poem
These 61 equal divisions of the octave,
though rare are assuredly a ROCK-tave (har har),
while the 3rd and 5th harmonics are about six cents sharp,
(and the flattish 15th poised differently on the harp),
the 7th and 11th err by less, around three,
and thus mayhap, a good orgone tuning found to be;
slightly sharp as well, is the 13th harmonic's place,
but the 9th and 17th lack near so much grace,
interestingly the 19th is good but a couple cents flat,
and the 21st and 23rd are but a cent or two sharp!
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +6.24 | +7.13 | -4.89 | -7.19 | -0.50 | +5.37 | -6.30 | -6.59 | -2.43 | +1.35 | +1.23 |
| Relative (%) | +31.7 | +36.2 | -24.9 | -36.5 | -2.5 | +27.3 | -32.0 | -33.5 | -12.4 | +6.9 | +6.3 | |
| Steps (reduced) |
97 (36) |
142 (20) |
171 (49) |
193 (10) |
211 (28) |
226 (43) |
238 (55) |
249 (5) |
259 (15) |
268 (24) |
276 (32) | |
Subsets and supersets
61edo is the 18th prime edo, after 59edo and before 67edo. 183edo, which triples it, corrects its approximation to many of the lower harmonics.
Intervals
| Steps | Cents | Approximate ratios | Ups and downs notation |
|---|---|---|---|
| 0 | 0 | 1/1 | D |
| 1 | 19.7 | ^D, vvE♭ | |
| 2 | 39.3 | ^^D, vE♭ | |
| 3 | 59 | 29/28, 32/31 | ^3D, E♭ |
| 4 | 78.7 | 22/21, 23/22 | ^4D, ^E♭ |
| 5 | 98.4 | 35/33 | v3D♯, ^^E♭ |
| 6 | 118 | 31/29 | vvD♯, ^3E♭ |
| 7 | 137.7 | 13/12 | vD♯, v4E |
| 8 | 157.4 | 23/21, 34/31, 35/32 | D♯, v3E |
| 9 | 177 | 21/19, 31/28 | ^D♯, vvE |
| 10 | 196.7 | 19/17 | ^^D♯, vE |
| 11 | 216.4 | 26/23 | E |
| 12 | 236.1 | ^E, vvF | |
| 13 | 255.7 | 22/19 | ^^E, vF |
| 14 | 275.4 | 34/29 | F |
| 15 | 295.1 | 19/16 | ^F, vvG♭ |
| 16 | 314.8 | 6/5 | ^^F, vG♭ |
| 17 | 334.4 | 17/14, 23/19 | ^3F, G♭ |
| 18 | 354.1 | ^4F, ^G♭ | |
| 19 | 373.8 | 26/21 | v3F♯, ^^G♭ |
| 20 | 393.4 | vvF♯, ^3G♭ | |
| 21 | 413.1 | 14/11, 33/26 | vF♯, v4G |
| 22 | 432.8 | F♯, v3G | |
| 23 | 452.5 | 13/10 | ^F♯, vvG |
| 24 | 472.1 | 21/16 | ^^F♯, vG |
| 25 | 491.8 | G | |
| 26 | 511.5 | 35/26 | ^G, vvA♭ |
| 27 | 531.1 | 19/14 | ^^G, vA♭ |
| 28 | 550.8 | 11/8 | ^3G, A♭ |
| 29 | 570.5 | 25/18, 32/23 | ^4G, ^A♭ |
| 30 | 590.2 | 31/22 | v3G♯, ^^A♭ |
| 31 | 609.8 | vvG♯, ^3A♭ | |
| 32 | 629.5 | 23/16 | vG♯, v4A |
| 33 | 649.2 | 16/11, 35/24 | G♯, v3A |
| 34 | 668.9 | 28/19 | ^G♯, vvA |
| 35 | 688.5 | ^^G♯, vA | |
| 36 | 708.2 | A | |
| 37 | 727.9 | 29/19, 32/21, 35/23 | ^A, vvB♭ |
| 38 | 747.5 | 20/13 | ^^A, vB♭ |
| 39 | 767.2 | ^3A, B♭ | |
| 40 | 786.9 | 11/7 | ^4A, ^B♭ |
| 41 | 806.6 | 35/22 | v3A♯, ^^B♭ |
| 42 | 826.2 | 21/13 | vvA♯, ^3B♭ |
| 43 | 845.9 | 31/19 | vA♯, v4B |
| 44 | 865.6 | 28/17, 33/20 | A♯, v3B |
| 45 | 885.2 | 5/3 | ^A♯, vvB |
| 46 | 904.9 | 32/19 | ^^A♯, vB |
| 47 | 924.6 | 29/17 | B |
| 48 | 944.3 | 19/11 | ^B, vvC |
| 49 | 963.9 | ^^B, vC | |
| 50 | 983.6 | 23/13 | C |
| 51 | 1003.3 | 34/19 | ^C, vvD♭ |
| 52 | 1023 | ^^C, vD♭ | |
| 53 | 1042.6 | 31/17 | ^3C, D♭ |
| 54 | 1062.3 | 24/13 | ^4C, ^D♭ |
| 55 | 1082 | v3C♯, ^^D♭ | |
| 56 | 1101.6 | vvC♯, ^3D♭ | |
| 57 | 1121.3 | 21/11 | vC♯, v4D |
| 58 | 1141 | 31/16 | C♯, v3D |
| 59 | 1160.7 | ^C♯, vvD | |
| 60 | 1180.3 | ^^C♯, vD | |
| 61 | 1200 | 2/1 | D |
Notation
Ups and downs notation
61edo can be notated using ups and downs notation using Helmholtz–Ellis accidentals:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|||||||||||||||||||
| Flat symbol |
Sagittal notation
This notation uses the same sagittal sequence as 54edo.
Evo flavor

Revo flavor

Evo-SZ flavor

In the diagrams above, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's primary comma (the comma it exactly represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it approximately represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this edo.
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3 | [97 -61⟩ | [⟨61 97]] | -1.97 | 1.97 | 10.0 |
| 2.3.5 | 20000/19683, 262144/253125 | [⟨61 97 142]] | -2.33 | 1.69 | 8.59 |
| 2.3.5.7 | 64/63, 2430/2401, 3125/3087 | [⟨61 97 142 172]] (61d) | -3.06 | 1.93 | 9.84 |
| 2.3.5.7 | 126/125, 1029/1024, 2240/2187 | [⟨61 97 142 171]] (61) | -1.32 | 2.29 | 11.7 |
Rank-2 temperaments
| Periods per 8ve |
Generator* | Cents* | Associated ratio* |
Temperament |
|---|---|---|---|---|
| 1 | 3\61 | 59.0 | 28/27 | Dodecacot (61de…) |
| 1 | 4\61 | 78.7 | 22/21 | Valentine (61) |
| 1 | 5\61 | 98.4 | 16/15 | Passion (61de…) / passionate (61) |
| 1 | 7\61 | 137.7 | 13/12 | Quartemka (61) |
| 1 | 9\61 | 177.0 | 10/9 | Modus (61de) / wollemia (61e) |
| 1 | 11\61 | 236.1 | 8/7 | Slendric (61) |
| 1 | 16\61 | 314.8 | 6/5 | Parakleismic (61d) |
| 1 | 23\61 | 452.5 | 13/10 | Maja (61d) |
| 1 | 25\61 | 491.8 | 4/3 | Quasisuper (61d) |
| 1 | 28\61 | 550.8 | 11/8 | Freivald (61) |
* Octave-reduced form, reduced to the first half-octave