Limmic temperaments: Difference between revisions
m Text replacement - "{{Technical data page}}<br><br>" to "{{Technical data page}}" |
Community poll result: 7-limit {28/27, 49/48} is the canonical extension of 5-limit {256/243}, hence *septimal blackwood* and no need of a distinct name. |
||
| Line 1: | Line 1: | ||
{{interwiki | {{interwiki | ||
| en = Limmic temperaments | |||
| de = Blackwood-Limmisch | | de = Blackwood-Limmisch | ||
| es = | | es = | ||
| ja = | | ja = | ||
| Line 8: | Line 8: | ||
'''Limmic temperaments''' are [[temperament]]s that [[temper out]] the Pythagorean limma, [[256/243]]. As a consequence, [[3/2]] is always represented by 3\5, 720 [[cent]]s assuming pure octaves. While quite sharp, this is close enough to a just fifth to serve as a fifth, and some people are fond of it. | '''Limmic temperaments''' are [[temperament]]s that [[temper out]] the Pythagorean limma, [[256/243]]. As a consequence, [[3/2]] is always represented by 3\5, 720 [[cent]]s assuming pure octaves. While quite sharp, this is close enough to a just fifth to serve as a fifth, and some people are fond of it. | ||
== | == Blackwood == | ||
Blackwood is the 5edo [[circle of fifths]] with an independent dimension for the harmonic 5. It can be described as the {{nowrap| 5 & 10 }} temperament. [[15edo]] is an obvious tuning. | |||
The only extension to the 7-limit that makes any sense is to map the [[7/4|harmonic seventh]] to 4\5, tempering out [[28/27]], [[49/48]], and [[64/63]]. This is known as ''blacksmith'' in earlier materials, including [[Graham Breed]]'s temperament finder. | |||
[[Subgroup]]: 2.3.5 | [[Subgroup]]: 2.3.5 | ||
| Line 18: | Line 21: | ||
: mapping generators: ~9/8, ~5 | : mapping generators: ~9/8, ~5 | ||
[[Optimal tuning]] ([[POTE]]): ~9/8 = | [[Optimal tuning]] ([[POTE]]): ~9/8 = 240.000, ~5/4 = 399.594 | ||
{{Optimal ET sequence|legend=1| 5, 10, 15 }} | {{Optimal ET sequence|legend=1| 5, 10, 15 }} | ||
[[Badness]]: 0.063760 | [[Badness]] (Smith): 0.063760 | ||
[[File:BlackwoodMajor 15edo.mp3]] [[:BlackwoodMajor 15edo.mp3|BlackwoodMajor 15edo.mp3]] | [[File:BlackwoodMajor 15edo.mp3]] [[:File:BlackwoodMajor 15edo.mp3|BlackwoodMajor 15edo.mp3]] | ||
Blackwood major scale in 15edo | Blackwood major scale in 15edo | ||
=== 7-limit === | === 7-limit (blacksmith) === | ||
[[File:blacksmith10.jpg|alt=blacksmith10.jpg|thumb|Lattice of | [[File:blacksmith10.jpg|alt=blacksmith10.jpg|thumb|Lattice of septimal blackwood]] | ||
[[Subgroup]]: 2.3.5.7 | [[Subgroup]]: 2.3.5.7 | ||
| Line 39: | Line 42: | ||
{{Multival|legend=1| 0 5 0 8 0 -14 }} | {{Multival|legend=1| 0 5 0 8 0 -14 }} | ||
[[Optimal tuning]] ([[POTE]]): ~8/7 = | [[Optimal tuning]] ([[POTE]]): ~8/7 = 240.000, ~5/4 = 392.767 | ||
{{Optimal ET sequence|legend=1| 5, 10, 15, 40b, 55b }} | {{Optimal ET sequence|legend=1| 5, 10, 15, 40b, 55b }} | ||
[[Badness]]: 0.025640 | [[Badness]] (Smith): 0.025640 | ||
=== 11-limit === | === 11-limit === | ||
| Line 52: | Line 55: | ||
Mapping: {{mapping| 5 8 0 14 29 | 0 0 1 0 -1 }} | Mapping: {{mapping| 5 8 0 14 29 | 0 0 1 0 -1 }} | ||
Optimal tuning (POTE): ~8/7 = | Optimal tuning (POTE): ~8/7 = 240.000, ~5/4 = 394.948 | ||
{{Optimal ET sequence|legend= | {{Optimal ET sequence|legend=0| 5, 10, 15, 40be, 55be, 70bde, 85bcde }} | ||
Badness: 0.024641 | Badness (Smith): 0.024641 | ||
==== 13-limit ==== | ==== 13-limit ==== | ||
| Line 65: | Line 68: | ||
Mapping: {{mapping| 5 8 0 14 29 7 | 0 0 1 0 -1 1 }} | Mapping: {{mapping| 5 8 0 14 29 7 | 0 0 1 0 -1 1 }} | ||
Optimal tuning (POTE): ~8/7 = | Optimal tuning (POTE): ~8/7 = 240.000, ~5/4 = 391.037 | ||
{{Optimal ET sequence|legend= | {{Optimal ET sequence|legend=0| 5, 10, 15, 25e, 40bef }} | ||
Badness: 0.020498 | Badness (Smith): 0.020498 | ||
=== Farrier === | === Farrier === | ||
| Line 78: | Line 81: | ||
Mapping: {{mapping| 5 8 0 14 -6 | 0 0 1 0 2 }} | Mapping: {{mapping| 5 8 0 14 -6 | 0 0 1 0 2 }} | ||
Optimal tuning (POTE): ~8/7 = | Optimal tuning (POTE): ~8/7 = 240.000, ~5/4 = 398.070 | ||
{{Optimal ET sequence|legend= | {{Optimal ET sequence|legend=0| 5e, 10e, 15 }} | ||
Badness: 0.029200 | Badness (Smith): 0.029200 | ||
==== 13-limit ==== | ==== 13-limit ==== | ||
| Line 91: | Line 94: | ||
Mapping: {{mapping| 5 8 0 14 -6 7 | 0 0 1 0 2 1 }} | Mapping: {{mapping| 5 8 0 14 -6 7 | 0 0 1 0 2 1 }} | ||
Optimal tuning (POTE): ~8/7 = | Optimal tuning (POTE): ~8/7 = 240.000, ~5/4 = 396.812 | ||
{{Optimal ET sequence|legend= | {{Optimal ET sequence|legend=0| 5e, 10e, 15 }} | ||
Badness: 0.022325 | Badness (Smith): 0.022325 | ||
=== Ferrum === | === Ferrum === | ||
| Line 104: | Line 107: | ||
Mapping: {{mapping| 5 8 0 14 6 | 0 0 1 0 1 }} | Mapping: {{mapping| 5 8 0 14 6 | 0 0 1 0 1 }} | ||
Optimal tuning (POTE): ~8/7 = | Optimal tuning (POTE): ~8/7 = 240.000, ~5/4 = 374.763 | ||
{{Optimal ET sequence|legend= | {{Optimal ET sequence|legend=0| 5e, 10 }} | ||
Badness: 0.030883 | Badness (Smith): 0.030883 | ||
== Blackweed == | == Blackweed == | ||
| Line 121: | Line 124: | ||
: sval mapping generators: ~9/8, ~11/7 | : sval mapping generators: ~9/8, ~11/7 | ||
[[Optimal tuning]] ([[Tp tuning|subgroup POTE]]): ~11/7 = 786.2215 | [[Optimal tuning]] ([[Tp tuning|subgroup POTE]]): ~9/8 = 240.000, ~11/7 = 786.2215 | ||
{{Optimal ET sequence|legend=1| 15, 20, 35b }} | {{Optimal ET sequence|legend=1| 15, 20, 35b }} | ||
Revision as of 14:27, 23 April 2025
- This is a list showing technical temperament data. For an explanation of what information is shown here, you may look at the technical data guide for regular temperaments.
Limmic temperaments are temperaments that temper out the Pythagorean limma, 256/243. As a consequence, 3/2 is always represented by 3\5, 720 cents assuming pure octaves. While quite sharp, this is close enough to a just fifth to serve as a fifth, and some people are fond of it.
Blackwood
Blackwood is the 5edo circle of fifths with an independent dimension for the harmonic 5. It can be described as the 5 & 10 temperament. 15edo is an obvious tuning.
The only extension to the 7-limit that makes any sense is to map the harmonic seventh to 4\5, tempering out 28/27, 49/48, and 64/63. This is known as blacksmith in earlier materials, including Graham Breed's temperament finder.
Subgroup: 2.3.5
Comma list: 256/243
Mapping: [⟨5 8 0], ⟨0 0 1]]
- mapping generators: ~9/8, ~5
Optimal tuning (POTE): ~9/8 = 240.000, ~5/4 = 399.594
Optimal ET sequence: 5, 10, 15
Badness (Smith): 0.063760
Blackwood major scale in 15edo
7-limit (blacksmith)
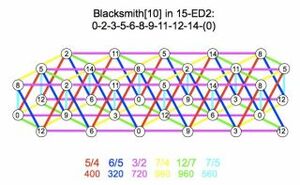
Subgroup: 2.3.5.7
Comma list: 28/27, 49/48
Mapping: [⟨5 8 0 14], ⟨0 0 1 0]]
Wedgie: ⟨⟨ 0 5 0 8 0 -14 ]]
Optimal tuning (POTE): ~8/7 = 240.000, ~5/4 = 392.767
Optimal ET sequence: 5, 10, 15, 40b, 55b
Badness (Smith): 0.025640
11-limit
Subgroup: 2.3.5.7.11
Comma list: 28/27, 49/48, 55/54
Mapping: [⟨5 8 0 14 29], ⟨0 0 1 0 -1]]
Optimal tuning (POTE): ~8/7 = 240.000, ~5/4 = 394.948
Optimal ET sequence: 5, 10, 15, 40be, 55be, 70bde, 85bcde
Badness (Smith): 0.024641
13-limit
Subgroup: 2.3.5.7.11.13
Comma list: 28/27, 40/39, 49/48, 55/54
Mapping: [⟨5 8 0 14 29 7], ⟨0 0 1 0 -1 1]]
Optimal tuning (POTE): ~8/7 = 240.000, ~5/4 = 391.037
Optimal ET sequence: 5, 10, 15, 25e, 40bef
Badness (Smith): 0.020498
Farrier
Subgroup: 2.3.5.7.11
Comma list: 28/27, 49/48, 77/75
Mapping: [⟨5 8 0 14 -6], ⟨0 0 1 0 2]]
Optimal tuning (POTE): ~8/7 = 240.000, ~5/4 = 398.070
Optimal ET sequence: 5e, 10e, 15
Badness (Smith): 0.029200
13-limit
Subgroup: 2.3.5.7.11.13
Comma list: 28/27, 40/39, 49/48, 66/65
Mapping: [⟨5 8 0 14 -6 7], ⟨0 0 1 0 2 1]]
Optimal tuning (POTE): ~8/7 = 240.000, ~5/4 = 396.812
Optimal ET sequence: 5e, 10e, 15
Badness (Smith): 0.022325
Ferrum
Subgroup: 2.3.5.7.11
Comma list: 28/27, 35/33, 49/48
Mapping: [⟨5 8 0 14 6], ⟨0 0 1 0 1]]
Optimal tuning (POTE): ~8/7 = 240.000, ~5/4 = 374.763
Badness (Smith): 0.030883
Blackweed
Blackweed is a variant of blackwood as it tempers out 256/243 alike but in the 2.3.11/7 subgroup. 20edo is close to the optimum, which has 4\20 as the period and 420¢ as the generator.
Subgroup: 2.3.11/7
Comma list: [8 -5⟩ = 256/243
Sval mapping: [⟨5 8 0], ⟨0 0 1]]
- sval mapping generators: ~9/8, ~11/7
Optimal tuning (subgroup POTE): ~9/8 = 240.000, ~11/7 = 786.2215