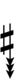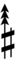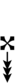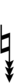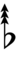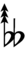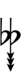42edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
ArrowHead294 (talk | contribs)
14,512 edits
BudjarnLambeth (talk | contribs)
autopatrolled, emailconfirmed
18,329 edits
 
(15 intermediate revisions by 5 users not shown)
Line 11: Line 11:
=== Odd harmonics ===
=== Odd harmonics ===
While not an accurate tuning on the full [[7-limit]], 42edo does an excellent job on the 2.9.15.7.33.39 [[k*N subgroups|2*42 subgroup]], having the same tuning on it as does [[84edo]]. On this subgroup 42 has the same [[comma]]s as 84.
While not an accurate tuning on the full [[7-limit]], 42edo does an excellent job on the 2.9.15.7.33.39 [[k*N subgroups|2*42 subgroup]], having the same tuning on it as does [[84edo]]. On this subgroup 42 has the same [[comma]]s as 84.
{{Harmonics in equal|42}}
{{Harmonics in equal|42}}
== JI approximation ==
{{Q-odd-limit intervals}}
=== Zeta peak index ===
{{ZPI
| zpi = 190
| steps = 41.9988672418690
| step size = 28.5721991759747
| tempered height = 2.689436
| pure height = 2.688894
| integral = 0.303886
| gap = 9.541545
| octave = 1200.03236539094
| consistent = 8
| distinct = 8
}}
== Regular temperament properties ==
{| class="wikitable center-4 center-5 center-6"
|-
! rowspan="2" | [[Subgroup]]
! rowspan="2" | [[Comma list]]
! rowspan="2" | [[Mapping]]
! rowspan="2" | Optimal<br>8ve stretch (¢)
! colspan="2" | Tuning error
|-
! [[TE error|Absolute]] (¢)
! [[TE simple badness|Relative]] (%)
|-
| 2.3
| {{monzo| 67 -42 }}
| {{mapping| 42 67 }}
| −3.89
| 3.88
| 13.57
|-
| 2.3.5
| 128/125, 5000000/4782969
| {{mapping| 42 67 98 }}
| −4.55
| 3.30
| 11.55
|-
| 2.3.5.7
| 64/63, 126/125, 6860/6561
| {{mapping| 22 35 51 62 }}
| −3.65
| 3.26
| 11.42
|}


=== Octave stretch ===
=== Octave stretch ===
Line 69: Line 19:
The following table compares three stretched tunings of 42edo:
The following table compares three stretched tunings of 42edo:


{| class="wikitable"
{| class="wikitable mw-collapsible mw-collapsed"
|-
|-
! Tuning
! Tuning
! [[42ed257/128]]
! [[42ed257/128]]
! [[1ed28.7c|APS720jot]]
! [[11ed6/5]]
! [[zpi|189zpi]]
! [[zpi|189zpi]]
! [[42edo]]
! [[42edo]]
Line 94: Line 44:
The following table compares three compressed tunings of 42edo:
The following table compares three compressed tunings of 42edo:


{| class="wikitable"
{| class="wikitable mw-collapsible mw-collapsed"
|-
|-
! Tuning
! Tuning
! [[42edo]]
! [[42edo]]
! [[1ed28.5c|APS715jot]]
! [[Equal-step tuning|34ed7/4]]
! [[191zpi]]
! [[191zpi]]
! [[ed255/128#42ed255/128|42ed255/128]]
! [[AS|AS123/121]]
|-
|-
! Steps / octave
! Steps / octave
Line 116: Line 66:
| colspan="5" | <span style="font-size: 0.75em;"><div style="text-align: center;">''“great” = 0-13% relative error • “good” = 13-27% • “okay” = 27-40% • “bad” = 40-50%''</div></span>
| colspan="5" | <span style="font-size: 0.75em;"><div style="text-align: center;">''“great” = 0-13% relative error • “good” = 13-27% • “okay” = 27-40% • “bad” = 40-50%''</div></span>
|}
|}
For a more detailed comparison see [[Table of stretched 42edo tunings]].


=== Subsets and supersets ===
=== Subsets and supersets ===
Line 127: Line 75:
! #
! #
! Cents
! Cents
! colspan="3" |[[Ups and Downs Notation]]
! colspan="3" | [[Ups and downs notation]]
|-
|-
| 0
| 0
| 0.000
| 0.0
| P1
| P1
| perfect unison
| perfect unison
Line 136: Line 84:
|-
|-
| 1
| 1
| 28.571
| 28.6
| ^1, m2
| ^1, m2
| up unison, minor 2nd
| up unison, minor 2nd
Line 142: Line 90:
|-
|-
| 2
| 2
| 57.143
| 57.1
| ^^1, ^m2
| ^^1, ^m2
| dup 1sn, upminor 2nd
| dup 1sn, upminor 2nd
Line 148: Line 96:
|-
|-
| 3
| 3
| 85.714
| 85.7
| ^^m2
| ^^m2
| dupminor 2nd
| dupminor 2nd
Line 154: Line 102:
|-
|-
| 4
| 4
| 114.286
| 114.3
| ^<sup>3</sup>m
| ^<sup>3</sup>m
| trupminor 2nd
| trupminor 2nd
Line 160: Line 108:
|-
|-
| 5
| 5
| 143.857
| 143.9
| v<sup>3</sup>M
| v<sup>3</sup>M
| trudmajor 2nd
| trudmajor 2nd
Line 166: Line 114:
|-
|-
| 6
| 6
| 171.429
| 171.4
| vvM2
| vvM2
| dudmajor 2nd
| dudmajor 2nd
Line 172: Line 120:
|-
|-
| 7
| 7
| 200.000
| 200.0
| vM2
| vM2
| downmajor 2nd
| downmajor 2nd
Line 178: Line 126:
|-
|-
| 8
| 8
| 228.571
| 228.6
| M2
| M2
| major 2nd
| major 2nd
Line 184: Line 132:
|-
|-
| 9
| 9
| 257.143
| 257.1
| m3
| m3
| minor 3rd
| minor 3rd
Line 190: Line 138:
|-
|-
| 10
| 10
| 285.714
| 285.7
| ^m3
| ^m3
| upminor 3rd
| upminor 3rd
Line 196: Line 144:
|-
|-
| 11
| 11
| 314.286
| 314.3
| ^^m3
| ^^m3
| dupminor 3rd
| dupminor 3rd
Line 202: Line 150:
|-
|-
| 12
| 12
| 342.857
| 342.9
| ^<sup>3</sup>m3
| ^<sup>3</sup>m3
| trupminor 3rd
| trupminor 3rd
Line 208: Line 156:
|-
|-
| 13
| 13
| 371.429
| 371.4
| v<sup>3</sup>M3
| v<sup>3</sup>M3
| trudmajor 3rd
| trudmajor 3rd
Line 214: Line 162:
|-
|-
| 14
| 14
| 400.000
| 400.0
| vvM3
| vvM3
| dudmajor 3rd
| dudmajor 3rd
Line 220: Line 168:
|-
|-
| 15
| 15
| 428.571
| 428.6
| vM3
| vM3
| downmajor 3rd
| downmajor 3rd
Line 226: Line 174:
|-
|-
| 16
| 16
| 457.143
| 457.1
| M3, v4
| M3, v4
| major 3rd, down 4th
| major 3rd, down 4th
Line 232: Line 180:
|-
|-
| 17
| 17
| 485.714
| 485.7
| P4
| P4
| perfect 4th
| perfect 4th
Line 238: Line 186:
|-
|-
| 18
| 18
| 514.286
| 514.3
| ^4
| ^4
| up 4th
| up 4th
Line 244: Line 192:
|-
|-
| 19
| 19
| 543.857
| 543.9
| ^^4
| ^^4
| dup 4th
| dup 4th
Line 250: Line 198:
|-
|-
| 20
| 20
| 571.429
| 571.4
| ^<sup>3</sup>4, ^^d5
| ^<sup>3</sup>4, ^^d5
| trup 4th, dupdim 5th
| trup 4th, dupdim 5th
Line 256: Line 204:
|-
|-
| 21
| 21
| 600.000
| 600.0
| v<sup>3</sup>A4, ^<sup>3</sup>d5
| v<sup>3</sup>A4, ^<sup>3</sup>d5
| trudaug 4th, trupdim 5th
| trudaug 4th, trupdim 5th
Line 262: Line 210:
|-
|-
| 22
| 22
| 628.571
| 628.6
| vvA4, v<sup>3</sup>5
| vvA4, v<sup>3</sup>5
| dudaug 4th, trud 5th
| dudaug 4th, trud 5th
Line 268: Line 216:
|-
|-
| 23
| 23
| 657.143
| 657.1
| vv5
| vv5
| dud 5th
| dud 5th
Line 274: Line 222:
|-
|-
| 24
| 24
| 685.714
| 685.7
| v5
| v5
| down 5th
| down 5th
Line 280: Line 228:
|-
|-
| 25
| 25
| 714.286
| 714.3
| P5
| P5
| perfect 5th
| perfect 5th
Line 286: Line 234:
|-
|-
| 26
| 26
| 742.857
| 742.9
| ^5, m6
| ^5, m6
| up 5th, minor 6th
| up 5th, minor 6th
Line 292: Line 240:
|-
|-
| 27
| 27
| 771.429
| 771.4
| ^m6
| ^m6
| upminor 6th
| upminor 6th
Line 298: Line 246:
|-
|-
| 28
| 28
| 800.000
| 800.0
| ^^m6
| ^^m6
| dupminor 6th
| dupminor 6th
Line 304: Line 252:
|-
|-
| 29
| 29
| 828.571
| 828.6
| ^<sup>3</sup>m6
| ^<sup>3</sup>m6
| trupminor 6th
| trupminor 6th
Line 310: Line 258:
|-
|-
| 30
| 30
| 857.143
| 857.1
| v<sup>3</sup>M6
| v<sup>3</sup>M6
| trudmajor 6th
| trudmajor 6th
Line 316: Line 264:
|-
|-
| 31
| 31
| 885.714
| 885.7
| vvM6
| vvM6
| dudmajor 6th
| dudmajor 6th
Line 322: Line 270:
|-
|-
| 32
| 32
| 914.286
| 914.3
| vM6
| vM6
| downmajor 6th
| downmajor 6th
Line 328: Line 276:
|-
|-
| 33
| 33
| 942.857
| 942.9
| M6
| M6
| major 6th
| major 6th
Line 334: Line 282:
|-
|-
| 34
| 34
| 971.429
| 971.4
| m7
| m7
| minor 7th
| minor 7th
Line 340: Line 288:
|-
|-
| 35
| 35
| 1000.000
| 1000.0
| ^m7
| ^m7
| upminor 7th
| upminor 7th
Line 346: Line 294:
|-
|-
| 36
| 36
| 1028.571
| 1028.6
| ^^m7
| ^^m7
| dupminor 7th
| dupminor 7th
Line 352: Line 300:
|-
|-
| 37
| 37
| 1057.143
| 1057.1
| ^<sup>3</sup>m7
| ^<sup>3</sup>m7
| trupminor 7th
| trupminor 7th
Line 358: Line 306:
|-
|-
| 38
| 38
| 1085.714
| 1085.7
| v<sup>3</sup>M7
| v<sup>3</sup>M7
| trudmajor 7th
| trudmajor 7th
Line 364: Line 312:
|-
|-
| 39
| 39
| 1114.286
| 1114.3
| vvM7
| vvM7
| dudmajor 7th
| dudmajor 7th
Line 370: Line 318:
|-
|-
| 40
| 40
| 1142.857
| 1142.9
| vM7
| vM7
| downmajor 7th
| downmajor 7th
Line 376: Line 324:
|-
|-
| 41
| 41
| 1171.429
| 1171.4
| M7, v8
| M7, v8
| major 7th, down 8ve
| major 7th, down 8ve
Line 382: Line 330:
|-
|-
| 42
| 42
| 1200.000
| 1200.0
| P8
| P8
| perfect 8ve
| perfect 8ve
Line 388: Line 336:
|}
|}


Chords can be named using ups and downs as C upminor, D downmajor seven, etc. See [[Ups and Downs Notation #Chords and Chord Progressions]].
Chords can be named using ups and downs as C upminor, D downmajor seven, etc. See [[Ups and downs notation #Chords and chord progressions]].


== Notation ==
== Notation ==
Line 394: Line 342:
Assuming the natural notes form a [[chain of fifths]], the major 2nd is 8 edosteps and the minor 2nd is only one. The naturals create a [[5edo]]-like scale, with two of the notes inflected by a [[comma]]-sized edostep:
Assuming the natural notes form a [[chain of fifths]], the major 2nd is 8 edosteps and the minor 2nd is only one. The naturals create a [[5edo]]-like scale, with two of the notes inflected by a [[comma]]-sized edostep:


D * * * * * * * * E F * * * * * * * * G * * * * * * * * A * * * * * * * * B C * * * * * * * * D
D * * * * * * * E F * * * * * * * G * * * * * * * A * * * * * * * B C * * * * * * * D


D♯ is next to E. The notation requires ups and downs with three arrows, and if chords are to be spelled correctly four or more arrows may be required in certain cases. For example, a {{dash|1/1, 5/4, 3/2, 9/5|med}} chord with a root on the key or fret midway between G and A would be written either as {{dash|v<sup>3</sup>G♯–v<sup>5</sup>B♯, v<sup>3</sup>D♯, vF♯|med}} or as {{dash|^<sup>3</sup>A♭, ^C, ^<sup>3</sup>E♭, ^<sup>5</sup>G♭}}. This is a dud dup-seven chord, written either as v<sup>3</sup>G♯vv,^^7 or as ^<sup>3</sup>A♭vv,^^7.
D♯ is next to E. The notation requires ups and downs with three arrows, and if chords are to be spelled correctly four or more arrows may be required in certain cases. For example, a {{dash|1/1, 5/4, 3/2, 9/5|med}} chord with a root on the edostep midway between G and A would be written either as {{dash|v<sup>3</sup>G♯–v<sup>5</sup>B♯, v<sup>3</sup>D♯, vF♯|med}} or as {{dash|^<sup>3</sup>A♭, ^C, ^<sup>3</sup>E♭, ^<sup>5</sup>G♭}}. This is a dud dup-seven chord, written either as v<sup>3</sup>G♯vv,^^7 or as ^<sup>3</sup>A♭vv,^^7.
 
In this table, dup is equivalent to quidsharp, trup is equivalent to quudsharp, trudsharp is equivalent to quup, dudsharp is equivalent to quip, etc.
{{sharpness-sharp7a}}


Alternatively, sharps and flats with arrows borrowed from [[Helmholtz–Ellis notation]] can be used:
Alternatively, sharps and flats with arrows borrowed from [[Helmholtz–Ellis notation]] can be used:
Line 404: Line 355:
=== Sagittal notation ===
=== Sagittal notation ===
==== Best fifth notation ====
==== Best fifth notation ====
This notation uses the same sagittal sequence as [[35edo#Second-best fifth notation|35b]].
This notation uses the same sagittal sequence as [[35edo #Second-best fifth notation|35b]].


===== Evo flavor =====
===== Evo flavor =====
Line 427: Line 378:


==== Second-best fifth notation ====
==== Second-best fifth notation ====
This notation uses the same sagittal sequence as [[47edo#Sagittal notation|47-EDO]], and is a superset of the notations for EDOs [[21edo#Sagittal notation|21]], [[14edo#Sagittal notation|14]], and [[7edo#Sagittal notation|7]].
This notation uses the same sagittal sequence as [[47edo#Sagittal notation|47edo]], and is a superset of the notations for edos [[21edo #Sagittal notation|21]], [[14edo #Sagittal notation|14]], and [[7edo #Sagittal notation|7]].


<imagemap>
<imagemap>
Line 437: Line 388:
default [[File:42b_Sagittal.svg]]
default [[File:42b_Sagittal.svg]]
</imagemap>
</imagemap>
== Approximation to JI ==
{{Q-odd-limit intervals}}
== Regular temperament properties ==
{| class="wikitable center-4 center-5 center-6"
|-
! rowspan="2" | [[Subgroup]]
! rowspan="2" | [[Comma list]]
! rowspan="2" | [[Mapping]]
! rowspan="2" | Optimal<br>8ve stretch (¢)
! colspan="2" | Tuning error
|-
! [[TE error|Absolute]] (¢)
! [[TE simple badness|Relative]] (%)
|-
| 2.3
| {{Monzo| 67 -42 }}
| {{Mapping| 42 67 }}
| −3.89
| 3.88
| 13.57
|-
| 2.3.5
| 128/125, 5000000/4782969
| {{Mapping| 42 67 98 }}
| −4.55
| 3.30
| 11.55
|-
| 2.3.5.7
| 64/63, 126/125, 6860/6561
| {{Mapping| 42 67 98 118 }}
| −3.65
| 3.26
| 11.42
|}


== Scales ==
== Scales ==
Line 449: Line 437:
* Seville/Sevond[14] 2nd mode: '''5 1 5 1 5 1 5 1 5 1 5 1 5 1'''
* Seville/Sevond[14] 2nd mode: '''5 1 5 1 5 1 5 1 5 1 5 1 5 1'''
* Seville/Sevond[21]: '''1 4 1 1 4 1 1 4 1 1 4 1 1 4 1 1 4 1 1 4'''
* Seville/Sevond[21]: '''1 4 1 1 4 1 1 4 1 1 4 1 1 4 1 1 4 1 1 4'''


; Subsets of MOS scales  
; Subsets of MOS scales  
Line 460: Line 449:
** Undecimal lydian-aeolian pentatonic: '''8 14 3 11 6'''
** Undecimal lydian-aeolian pentatonic: '''8 14 3 11 6'''
** Yokai pentatonic: '''3 14 8 3 14'''
** Yokai pentatonic: '''3 14 8 3 14'''
; Approximations of [[gamelan]] scales:
* 5-tone pelog: 4 5 15 3 15
* 7-tone pelog: 4 5 9 6 3 10 5
* 5-tone slendro: 8 9 8 9 8


== Instruments ==
== Instruments ==
; Fretted instruments
=== Lumatone ===
; [[Skip fretting system 42 3 11]]
; Lumatone
{{main|Lumatone mapping for 42edo}}
{{main|Lumatone mapping for 42edo}}
=== Skip fretting ===
'''[[Skip fretting]] system 42 3 11''': One way to play [[42edo]] on a [[14edo]] guitar is to tune the strings 11\42, or approximately a [[just]] 6/5, apart. All examples on this page are for 7-string guitar.
; Prime intervals
1/1: string 2 open
2/1: string 5 fret 3
3/2: string 4 fret 1 and string 7 fret 4
5/4: string 3 fret 1
7/4: string 1 fret 1 and string 4 fret 4
11/8: string 7 fret 2
13/8: string 3 fret 6
17/16: string 1 fret 5
19/16: string 1 fret 7
23/16: string 4 open and string 7 fret 3
29/16: string 5 fret 1
31/16: string 1 fret 3 and string 4 fret 6
; Chords
Minor 7th: 100123X


== Music ==
== Music ==
Line 477: Line 501:
=== 21st century ===
=== 21st century ===
; [[Bryan Deister]]
; [[Bryan Deister]]
* [https://www.youtube.com/watch?v=PJw8gZyNPjg ''improv 42edo''] (2023)
* [https://www.youtube.com/watch?v=ljaSpsQP2qc ''Improvisation in 42edo''] (2023), transcribed by [[Stephen Weigel]] (2024)
* [https://www.youtube.com/watch?v=ljaSpsQP2qc ''Improvisation in 42edo''] (2023), transcribed by [[Stephen Weigel]] (2024)


Line 492: Line 517:


[[Category:Augene]]
[[Category:Augene]]
[[Category:Todo:add rank 2 temperaments table]]
{{Todo|review|add rank 2 temperaments table}}

Latest revision as of 05:34, 22 August 2025

← 41edo 42edo 43edo →
Prime factorization 2 × 3 × 7
Step size 28.5714 ¢ 
Fifth 25\42 (714.286 ¢)
Semitones (A1:m2) 7:1 (200 ¢ : 28.57 ¢)
Dual sharp fifth 25\42 (714.286 ¢)
Dual flat fifth 24\42 (685.714 ¢) (→ 4\7)
Dual major 2nd 7\42 (200 ¢) (→ 1\6)
Consistency limit 7
Distinct consistency limit 7

42 equal divisions of the octave (abbreviated 42edo or 42ed2), also called 42-tone equal temperament (42tet) or 42 equal temperament (42et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 42 equal parts of about 28.6 ¢ each. Each step represents a frequency ratio of 21/42, or the 42nd root of 2.

Theory

42edo has a patent val fifth (the step of which is not from 7edo, this being a first for edos of the form 7n) and a third both over 12 cents sharp, using the same 400-cent interval to represent 5/4 as does 12edo, which means it tempers out 128/125. In the 7-limit, it tempers out 64/63 and 126/125, making it a tuning supporting the augene temperament.

42edo is on the optimal ET sequence of the eugene, joan, lemba, neutron, qeema, seville, sevond, skateboard, tritikleismic and vines temperaments.

42edo is a diatonic edo because its 5th falls between 4\7 = 686 ¢ and 3\5 = 720 ¢. 42edo is one of the most difficult diatonic edos to notate, because no other diatonic edo's fifth is as sharp (see 47edo for the opposite extreme).

Odd harmonics

While not an accurate tuning on the full 7-limit, 42edo does an excellent job on the 2.9.15.7.33.39 2*42 subgroup, having the same tuning on it as does 84edo. On this subgroup 42 has the same commas as 84.


Approximation of odd harmonics in 42edo
Harmonic 3 5 7 9 11 13 15 17 19 21 23
Error Absolute (¢) +12.3 +13.7 +2.6 -3.9 -8.5 -12.0 -2.6 +9.3 -11.8 -13.6 +0.3
Relative (%) +43.2 +47.9 +9.1 -13.7 -29.6 -41.8 -8.9 +32.7 -41.3 -47.7 +1.0
Steps
(reduced) 		67
(25) 		98
(14) 		118
(34) 		133
(7) 		145
(19) 		155
(29) 		164
(38) 		172
(4) 		178
(10) 		184
(16) 		190
(22)

Octave stretch

42edo’s inaccurate 3rd and 5th harmonics can be greatly improved through stretching or compressing octaves. Both approaches work about equally well but in opposite directions, giving two quite different flavors of tuning to play with.

The following table compares three stretched tunings of 42edo:

Tuning 42ed257/128 11ed6/5 189zpi 42edo
Steps / octave ~41.77 ~41.81 ~41.83 42.00
Approximation
of harmonics 		great: 5
good: 2, 3, 7
okay:
bad: 11, 13 		great: 5
good: 2, 3
okay: 7, 11, 13
bad: 		great: 5
good: 2, 13
okay: 3, 11
bad: 7 		great: 2, 7
good:
okay: 11
bad: 3, 5, 13
“great” = 0-13% relative error • “good” = 13-27% • “okay” = 27-40% • “bad” = 40-50%

The following table compares three compressed tunings of 42edo:

Tuning 42edo 34ed7/4 191zpi AS123/121
Steps / octave 42.00 ~42.10 ~42.19 ~42.24
Approximation
of harmonics 		great: 2, 7
good:
okay: 11
bad: 3, 5, 13 		great: 2
good: 5, 7, 13
okay: 3, 11
bad: 		great: 5, 11, 13
good: 2, 3
okay:
bad: 7 		great: 3, 5, 11
good: 2
okay: 13
bad: 7
“great” = 0-13% relative error • “good” = 13-27% • “okay” = 27-40% • “bad” = 40-50%

Subsets and supersets

Since 42 factors into 2 × 3 × 7, 42edo contains subset edos 2, 3, 6, 7, 14, and 21.

Intervals

# Cents Ups and downs notation
0 0.0 P1 perfect unison D
1 28.6 ^1, m2 up unison, minor 2nd ^D, Eb
2 57.1 ^^1, ^m2 dup 1sn, upminor 2nd ^^D, ^Eb
3 85.7 ^^m2 dupminor 2nd ^^Eb
4 114.3 ^3m trupminor 2nd ^3Eb
5 143.9 v3M trudmajor 2nd v3E
6 171.4 vvM2 dudmajor 2nd vvE
7 200.0 vM2 downmajor 2nd vE
8 228.6 M2 major 2nd E
9 257.1 m3 minor 3rd F
10 285.7 ^m3 upminor 3rd ^F
11 314.3 ^^m3 dupminor 3rd ^^F
12 342.9 ^3m3 trupminor 3rd ^3F
13 371.4 v3M3 trudmajor 3rd v3F#
14 400.0 vvM3 dudmajor 3rd vvF#
15 428.6 vM3 downmajor 3rd vF#
16 457.1 M3, v4 major 3rd, down 4th F#, vG
17 485.7 P4 perfect 4th G
18 514.3 ^4 up 4th ^G
19 543.9 ^^4 dup 4th ^^G
20 571.4 ^34, ^^d5 trup 4th, dupdim 5th ^3G, ^^Ab
21 600.0 v3A4, ^3d5 trudaug 4th, trupdim 5th v3G#, ^3Ab
22 628.6 vvA4, v35 dudaug 4th, trud 5th vvG#, v3A
23 657.1 vv5 dud 5th vvA
24 685.7 v5 down 5th vA
25 714.3 P5 perfect 5th A
26 742.9 ^5, m6 up 5th, minor 6th ^A, Bb
27 771.4 ^m6 upminor 6th ^Bb
28 800.0 ^^m6 dupminor 6th ^^Bb
29 828.6 ^3m6 trupminor 6th ^3Bb
30 857.1 v3M6 trudmajor 6th v3B
31 885.7 vvM6 dudmajor 6th vvB
32 914.3 vM6 downmajor 6th vB
33 942.9 M6 major 6th B
34 971.4 m7 minor 7th C
35 1000.0 ^m7 upminor 7th ^C
36 1028.6 ^^m7 dupminor 7th ^^C
37 1057.1 ^3m7 trupminor 7th ^3C
38 1085.7 v3M7 trudmajor 7th v3C#
39 1114.3 vvM7 dudmajor 7th vvC#
40 1142.9 vM7 downmajor 7th vC#
41 1171.4 M7, v8 major 7th, down 8ve C#, vD
42 1200.0 P8 perfect 8ve D

Chords can be named using ups and downs as C upminor, D downmajor seven, etc. See Ups and downs notation #Chords and chord progressions.

Notation

Ups and downs notation

Assuming the natural notes form a chain of fifths, the major 2nd is 8 edosteps and the minor 2nd is only one. The naturals create a 5edo-like scale, with two of the notes inflected by a comma-sized edostep:

D * * * * * * * E F * * * * * * * G * * * * * * * A * * * * * * * B C * * * * * * * D

D♯ is next to E. The notation requires ups and downs with three arrows, and if chords are to be spelled correctly four or more arrows may be required in certain cases. For example, a 1/1 – 5/4 – 3/2 – 9/5 chord with a root on the edostep midway between G and A would be written either as v3G♯–v5B♯ – v3D♯ – vF♯ or as ^3A♭ – ^C – ^3E♭ – ^5G♭. This is a dud dup-seven chord, written either as v3G♯vv,^^7 or as ^3A♭vv,^^7.

In this table, dup is equivalent to quidsharp, trup is equivalent to quudsharp, trudsharp is equivalent to quup, dudsharp is equivalent to quip, etc.

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Sharp symbol                
                 
Flat symbol              
                 

Alternatively, sharps and flats with arrows borrowed from Helmholtz–Ellis notation can be used:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
Sharp symbol  
Flat symbol

Sagittal notation

Best fifth notation

This notation uses the same sagittal sequence as 35b.

Evo flavor
Sagittal notationPeriodic table of EDOs with sagittal notationapotome-fraction notation
Revo flavor
Sagittal notationPeriodic table of EDOs with sagittal notationapotome-fraction notation

Second-best fifth notation

This notation uses the same sagittal sequence as 47edo, and is a superset of the notations for edos 21, 14, and 7.

Sagittal notationPeriodic table of EDOs with sagittal notationlimma-fraction notation

Approximation to JI

The following tables show how 15-odd-limit intervals are represented in 42edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 42edo (direct approximation, even if inconsistent)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
5/3, 6/5 1.356 4.7
15/8, 16/15 2.554 8.9
7/4, 8/7 2.603 9.1
13/10, 20/13 2.929 10.3
13/11, 22/13 3.495 12.2
9/8, 16/9 3.910 13.7
13/12, 24/13 4.284 15.0
11/9, 18/11 4.551 15.9
15/14, 28/15 5.157 18.0
15/11, 22/15 5.906 20.7
11/10, 20/11 6.424 22.5
9/7, 14/9 6.513 22.8
11/6, 12/11 7.780 27.2
13/9, 18/13 8.046 28.2
11/8, 16/11 8.461 29.6
15/13, 26/15 9.402 32.9
7/6, 12/7 9.728 34.0
9/5, 10/9 10.975 38.4
11/7, 14/11 11.063 38.7
7/5, 10/7 11.084 38.8
13/8, 16/13 11.956 41.8
3/2, 4/3 12.331 43.2
5/4, 8/5 13.686 47.9
13/7, 14/13 14.013 49.0
15-odd-limit intervals in 42edo (patent val mapping)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
5/3, 6/5 1.356 4.7
7/4, 8/7 2.603 9.1
13/11, 22/13 3.495 12.2
11/8, 16/11 8.461 29.6
7/6, 12/7 9.728 34.0
9/5, 10/9 10.975 38.4
11/7, 14/11 11.063 38.7
7/5, 10/7 11.084 38.8
13/8, 16/13 11.956 41.8
3/2, 4/3 12.331 43.2
5/4, 8/5 13.686 47.9
13/7, 14/13 14.559 51.0
11/6, 12/11 20.792 72.8
9/7, 14/9 22.059 77.2
11/10, 20/11 22.147 77.5
15/14, 28/15 23.414 82.0
13/12, 24/13 24.287 85.0
9/8, 16/9 24.661 86.3
13/10, 20/13 25.643 89.7
15/8, 16/15 26.017 91.1
11/9, 18/11 33.122 115.9
15/11, 22/15 34.478 120.7
13/9, 18/13 36.618 128.2
15/13, 26/15 37.973 132.9

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3 [67 -42⟩ [⟨42 67]] −3.89 3.88 13.57
2.3.5 128/125, 5000000/4782969 [⟨42 67 98]] −4.55 3.30 11.55
2.3.5.7 64/63, 126/125, 6860/6561 [⟨42 67 98 118]] −3.65 3.26 11.42

Scales

Main article: List of MOS scales in 42edo
MOS scales
  • Eugene/Tritikleismic[9]: 3 8 3 3 8 3 3 8 3
  • Eugene/Tritikleismic[15]: 3 3 2 3 3 3 3 2 3 3 3 3 2 3 3
  • Lemba[16]: 3 2 3 2 3 3 2 3 3 2 3 2 3 3 2 3
  • Qeema/Skateboard[15]: 2 5 2 2 2 5 2 2 2 5 2 2 2 5 2
  • Qeema/Skateboard[19]: 2 2 3 2 2 2 2 3 2 2 2 3 2 2 2 2 3 2 2
  • Seville/Sevond[14] 1st mode: 1 5 1 5 1 5 1 5 1 5 1 5 1 5
  • Seville/Sevond[14] 2nd mode: 5 1 5 1 5 1 5 1 5 1 5 1 5 1
  • Seville/Sevond[21]: 1 4 1 1 4 1 1 4 1 1 4 1 1 4 1 1 4 1 1 4


Subsets of MOS scales

(Names used are idiosyncratic.)

  • Eugene/Tritikleismic[9]
    • Groovy aeolian pentatonic: 11 6 8 3 14
    • Otonal mixolydian pentatonic: 14 3 8 11 6
    • Pseudo-equipentatonic: 11 6 8 6 11
    • Septimal melodic minor pentatonic: 8 3 14 14 3
    • Septimal Picardy pentatonic: 8 6 11 3 14
    • Undecimal lydian-aeolian pentatonic: 8 14 3 11 6
    • Yokai pentatonic: 3 14 8 3 14


Approximations of gamelan scales
  • 5-tone pelog: 4 5 15 3 15
  • 7-tone pelog: 4 5 9 6 3 10 5
  • 5-tone slendro: 8 9 8 9 8

Instruments

Lumatone

Main article: Lumatone mapping for 42edo

Skip fretting

Skip fretting system 42 3 11: One way to play 42edo on a 14edo guitar is to tune the strings 11\42, or approximately a just 6/5, apart. All examples on this page are for 7-string guitar.

Prime intervals

1/1: string 2 open

2/1: string 5 fret 3

3/2: string 4 fret 1 and string 7 fret 4

5/4: string 3 fret 1

7/4: string 1 fret 1 and string 4 fret 4

11/8: string 7 fret 2

13/8: string 3 fret 6

17/16: string 1 fret 5

19/16: string 1 fret 7

23/16: string 4 open and string 7 fret 3

29/16: string 5 fret 1

31/16: string 1 fret 3 and string 4 fret 6

Chords

Minor 7th: 100123X

Music

Modern renderings

Johann Sebastian Bach
Bing Crosby

21st century

Bryan Deister
James Kukula
Budjarn Lambeth
Herman Miller
Mundoworld
Retrieved from "https://en.xen.wiki/index.php?title=42edo&oldid=208012"