Talk:IFDO
Critique of naming system
Recently, Flora introduced the idea of conceptualizing equal-step tunings in terms of various well-known mathematical means such as the geometric mean, arithmetic mean, and harmonic mean. To be clear, these were not novel tunings she proposed; rather, she introduced yet another way of identifying and reasoning about this existing equal-step family of tunings which have already been studied and named ad nauseum throughout xenharmonic history.
Flora wisely chose not to suggest identifying tunings by the "harmonic mean", due to the established and contradictory meaning of "harmonic" in our musical field. I have pushed back against her use of "arithmetic mean" for similar reasons; Shaahin Mohajeri introduced it to the xen lexicon in 2006 via his Arithmetic Division of the Octave (ADO) tuning (see here: https://yahootuninggroupsultimatebackup.github.io/makemicromusic/topicId_13427.html#13427), where Shaahin used the word as a reference to the mathematical concept of an arithmetic sequence/progression, which is a sequence formed by repeatedly adding a constant. So what Shaahin did was assume the constant was in terms of frequency. Another thing he did was use a word for an open sequence to describe a tuning which is a periodic division of an interval. In 2021, along with Billy Stiltner and Paul Erlich, I developed a naming system for equal-step tunings which handles both periodic divisions and open sequences. In this system, the former are "Equal Divisions", as in the overwhelming popular Equal Divisions of the Octave (EDO); the latter are "Arithmetic Sequences". So we borrowed Shaahin's use of "arithmetic", but repurposed it in a more appropriate way: for sequences, not divisions. And another thing we improved over Shaahin's concept was to treat pitch, not frequency, as the default musical resource; this agrees with the overwhelming popularity of EDOs, which are in fact equal pitch divisions of the octave. In short, we extended the established basic ideas of equal divisions and arithmetic sequences of pitch to the two other fundamental musical resources of frequency and length. We felt comfortable with the fact Shaahin's ADO made different assumptions than our system, because Shaahin was clearly not attempting to develop a full, internally-consistent system like we were (one need only look to his other tuning, EDL, which is neither consistent with ADO nor EDO). However, Flora does indeed seem to be attempting to develop a rivalling full internally-consistent system to the one we developed already. And my concern with Flora's proposal is that it uses the word "arithmetic" to describe tuning systems in this family but in a different sense than "arithmetic" has been being used historically. In the case of Shaahin's ADO, the two meanings happen to coincide. But when she extends the idea to "inverse-arithmetic mean", as a substitute for the even more unusable "harmonic mean", her meaning of "arithmetic" comes into conflict with our system's meaning. And we can see another negative consequence of Flora's proposal in that a page cropped up for "Arithmetic MOS", where CompactStar has gotten comfortable with treating "arithmetic" as synonymous with "of frequency" (see: https://en.xen.wiki/w/Talk:Arithmetic_MOS_scale).
Recently on the Discord server, CompactStar took a step toward generalizing Flora's concept of using mathematical means to describe equal-step tunings when he proposed the concept of an RD, where an interval is divided into equal parts according to the root mean square (RMS). Flora took the next step, showing that any power mean (p-mean) could be used in this way to define an equal-step tuning. The geometric mean is p = 0, the arithmetic mean is p = 1, the harmonic mean is p = -1, and the quadratic mean (same as RMS) is p = 2. So p = 0 corresponds with ED's/AS's of pitch, p = 1 corresponds with ED's/AS's of frequency, and p = -1 corresponds with ED's/AS's of length (of strings, resonating chambers, etc.). But this p = 2 corresponds with a new type of musical resource, on the other side of frequency yet from pitch. This is a novel tuning system and worth studying.
In my opinion, originally, Flora's idea of using mathematical means to describe these popular equal-step tunings was unnecessarily obscure, in comparison with the system I helped design a couple years ago which is much more directly accessible to practicing musicians, through its use of the three actual physical/psychoacoustic resources of frequency, pitch, and length. However, this new idea which leverages mathematical power means to explore new tunings, and describe this family of tunings along a smooth continuum — e.g. there's potential for tunings defined somewhere between equal divisions of frequency and pitch like 1/2MD, or between pitch and length e.g. (-1/2)MD — finally justifies Flora's concept. And so, if mathematical means are to be used in this way, then I would strongly prefer use of the power mean's power in the name, rather than "arithmetic" and the new coinage "inverse-arithmetic" (which is a bit strained anyway) as in AD and ID. I hope that in consideration of all of this, Flora and CompactStar will consider switching to refer to AD's as 1MD's and ID's as (-1)MD's. --Cmloegcmluin (talk) 19:06, 27 March 2023 (UTC)
- A few points to add:
- I disagree I used the term arithmetic differently from the sense of Shaahin Mohajeri (2006), altho I admit it differs from Billy Stiltner et al (2021). As one way to see it, frequency is implied as the default measurement – but more appropriately the measurement is determined by the specific word in the place. Using arithmetic for anything other than frequency would bug me, just as harmonic mean bugs us since its defined in terms of length.
- I suppose the letter M stands for mean, such that the full name is m-mean division? Not that I disapprove of a change of the page title, at this point I hesitate to say it's the right word choice. Specifically, whenever there's a mean there's also a sequence, including the fractional-order ones, since the mean is really an element of a special case of a sequence. So this concept is based on not exactly means but sequences. I'd consider the full name is order-m division or order-m sequence division.
- I believe m = 1 and m = -1 deserve verbal names (even tho they're disputed) in addition to the formal one, just as m = 0 does.
- I'm sorry, but you are simply wrong to disagree with my point that you used "arithmetic" differently than Shaahin. Frequency being implied as the default measurement is the only valid way to see this. If you check the link provided, it is absolutely clear that Shaahin intended it to refer to arithmetic sequences/progressions, and not to the arithmetic mean. I'm sorry that using arithmetic for anything other than frequency bugs you, but this is the way it has been done since 2006 and I hope that even if it doesn't work for you that you will respect those for whom it has been working well.
- Yes, the M stands for mean. It's possible that you're using "sequence" and "division" differently than they are used in the existing system; I cannot understand what a "sequence division" could be in terms of what has already been established, since those are two mutually exclusive tuning types: one open-ended, the other periodic. I wasn't explicit about this in my previous post, but this application of power means to equal-step tunings applies well for both divisions and sequences. That is, I would expect that an EFD (equal frequency division) would be equivalent to a 1MD (1-mean division), and an AFS (arithmetic frequency sequence) would be equivalent to a 1MS (1-mean sequence); similarly, an ELD (equal length division) would be equivalent to a (-1)MD ((-1)-mean division) and an ALS (arithmetic length sequence) would be equivalent to a (-1)MS ((-1)-mean sequence). The same for E(P)D = 0MD and APS = 0MS, too.
- I think AMD for "arithmetic mean division" as a substitute for 1MD, GMD for "geometric mean division" as a substitute for 0MD, and HMD for "harmonic mean division" as a substitute for (-1)MD, would all be fine. Using simply AD and HD (or ID) is not acceptable, because it is incompatible with ED, implying that in an ED, the frequencies of pitches are related to their immediate neighbors by the "equal mean" of their frequencies; however, the "equal mean" does not exist, so this is not true. The established system simply assumes pitch to have naturally been the default resource, and so an ED is an E(P)D, and this was extended to EFD and ELD.
- --Cmloegcmluin (talk) 18:23, 28 March 2023 (UTC)
- Just becuz you so framed it isn't evidence that I be wrong. You showed it yourself that Shaahin's ado was originally intended to be measured in frequency, where as the extension I made involves viewing the word as indicating the scale of measurement, as in AD vs ED vs ID. The other problem, which also has to do with your second point, is that you don't realize the mean is an element of a special case of the sequence/progression, so my extension isn't based exactly on the means, but a uniform of both. FloraC (talk) 03:48, 29 March 2023 (UTC)
- Adding my grain of salt: I don't think it's wrong to have both a systematic naming system for theorists who want to get everything covered unambiguously and, in parallel, a set of everyday terms for musicians. I view cmloegcmluin's system of harmonotonic tunings as a systematic naming system, whereas the term "IDO" tries to follow the footsteps of "EDO" as a more colloquial term (i.e. not as unambiguous, but understood by most in context). I personally don't like "IDO" because I find it much harder to understand compared to "subharmonic series segment" (used by Sevish and probably more before/after him) or "undertone scale" (used by Andrew Heathwaite and probably more before/after him), while also not being as explicit as cmloegcmluin's systematic terminology. There are also shorthand notations like 24::12 (pronounced as "subharmonics 24 to 12") that convey more effectively the idea of "12ido" that aren't much longer or harder to say than "12ido". As for fractional-order tuning systems, I think it's better to start by developing a systematic naming system, if only because it might not turn out useful or necessary to make it musician-friendly later. --Fredg999 (talk) 01:11, 29 March 2023 (UTC)
- I don't see how inverse-arithmetic division could be described as more "colloquial" than equal division of length. To me it seems impossible to argue that this is more of an "everyday term for musicians", since ID references a recently made-up variation on a mathematical mean which most musicians do not know in the first place, while ELD references the physical property of string or resonating chamber length that practicing musicians actually physically deal with. The EFD/E(P)D/ELD system is both the unambiguous and comprehensive system for theorists as well as the more accessible system for music makers, and it has slight (2 years) historical precedence. --Cmloegcmluin (talk) 02:17, 29 March 2023 (UTC)
- In case I wasn't clear, I wasn't stating that IDO is more colloquial than EDL/ELD, but rather that IDO seems derived and inspired by EDO, which is more colloquial than its systematic counterpart EPDO. I agree that "equal length division" and "equal frequency division" are clear enough to be used directly by musicians, especially when using irrational numbers. As for (sub)harmonic series segment, now that I think about it, I believe they cover only a subset of otonal/utonal divisions/sequences (e.g. 4:7:10:...:25:28 is not a harmonic series segment, but it is an OD/OS), so unless I'm mistaken, it might be good to keep both terms around to describe the different concepts. --Fredg999 (talk) 03:01, 29 March 2023 (UTC)
- Ah, sorry, I see what you mean now. However, now I don't see how ID "seems derived and inspired by" ED any more than EFD and ELD are derived and inspired by E(P)D. --Cmloegcmluin (talk) 03:43, 29 March 2023 (UTC)
- I have documented the history here: ADO#History, and also updated the IDO page accordingly. Because this way of using "arithmetic" is contentious:
- a) I have suggested that the pages Arithmetic interval chain and Arithmetic MOS scale) be withdrawn from the main wiki and changed to user pages, at least for now (see: Talk:Arithmetic interval chain and Talk:Arithmetic MOS scale).
- b) I have added ODO and UDO as additional equivalent bolded terms to all of the recently created ADO and IDO pages, and created redirect pages to them. However, I don't think this is quite enough; I believe that the redirects should be swapped so that the ODO and UDO pages are the destination pages (and accordingly that the order of the bolded terms be switched on each page so that ODO and UDO take precedence, and ODO/UDO used afterward throughout each page).
- c) I also suggest that the ADO and IDO infoboxes be changed to the ODO and UDO infoboxes.
- I have not taken those actions yet, however, because I did not create all these pages myself, and I want to respect CompactStar's authorship and give them a chance to weigh in on the matter. I'm sorry this is a lot of changes and suggested further changes, but I was just not available to spend my time and energy on this issue while it was beginning to balloon out of control these past couple months. --Cmloegcmluin (talk) 18:43, 30 March 2023 (UTC)
- Sorry, but I still don't really understand your concern about OD and UD. On the Talk page you mention (Talk:Arithmetic tuning) you said something about "lack of orthogonality". When I pressed you to explain this idea, you wrote: "I explained the lack of orthogonality as 'one specification is often encompassed by another', and so by having orthogonality our specifications would be minimal and disjoint from each other. Note that this is not abouting deprecating the concepts and the names, only how we specify individual tuning systems." I'm sorry I dropped that conversational thread, and I'm really sorry about this too, but I still can't figure out what you're trying to say here. Could you try explaining in another way, please?
- One thing I'm confused about is that I thought recently on Discord you said you preferred OD and UD over EFD and ELD, though it was on the condition that they be able to apply to divisions of irrational intervals and therefore be non-JI (which I noted was an unacceptable condition). I only find it slightly less unacceptable to use EFD where OD is possible, because of the implication that an EFD must be non-JI. But maybe I'm just a bit lost because there have been so many subtleties to this discussion, and it has been fragmented in so many places, and it's taken place relatively slowly over the course of many years, so it's hard for me to keep everything straight. I have probably accidentally said inconsistent things here or there, so I sincerely apologize if you find that I wasted your time or confused you due to something like that.
- Oh, but I did figure out what you meant by a "sequence division" in the discussion above. I think my confusion arose because we're using "sequence" in two different ways. The system I designed with Paul and Billy uses sequence as opposed to a division, i.e. open-ended as opposed to periodic. But you're using sequence as in arithmetic sequence, geometric sequence, harmonic sequence, etc. (which are closely related to arithmetic mean, geometric mean, harmonic mean, etc.) Sorry I didn't understand that immediately. So, I propose that since in your context, we can use "progression" as an exact synonym, we stick to using "progression" for that context, to avoid further miscommunication. Hopefully that works for you, too. --Cmloegcmluin (talk) 23:55, 31 March 2023 (UTC)
- Hmmm, here's another way to speak of odo's lack of orthogonality: it contains redundant information, as both otonal and octave imply rationality and not becuz it has to be designed this way. An orthogonal system will have these kind of redundancies minimized, like that orthogonality in linear algebra, you know. In this case ado or efdo is sufficient to uniquely identify the object with rationality conveyed thru the divided interval itself, so it's advantageous. Using otonal will introduce a kind of perplexity in which we can find "grammatically" possible but "semantically" invalid combinations such as *odφ.
- I can see how sequence means two different things. What I was calling the sequence was also known as "linspace" in some programming libraries, if that makes any sense to you. For the open-ended sequence, let's say progression from now on.
- I'm glad we're in agreement on the progression vs. sequence thing. Thanks.
- And okay, I think I finally understand what you're saying now re: "orthogonality". Thank you for your patience with me. However, it doesn't dissuade me from seeing ODO as the more appropriate equivalence to ADO.
- I've tried to use an extended analogy to deal with this issue. Now, this maybe isn't a perfect or exact analogy, nor is it any simpler than the music problem we're looking at, but perhaps a problem with an matching structure but different contents will give us a new opportunity to reason through our disagreement. Maybe it'll give us a clean foundation from where we can identity places our assumptions have diverged.
- So suppose we have a situation where the easy, obvious, and popular things to care about are sets of circle centers. Then someone points out that we might consider ellipses, too, but when they start experimenting with this, they realize that technically what we should be interested in when we generalize circles like this are the lower of these shapes' foci, not their centers.
- Then people come along to give the community systematic ways to name this stuff. For example, they could use n-LFSp: n-cardinality Lower Foci Sets of shapes which are somehow specified by p. Perhaps this p could be the proportion between the distance between foci and the radius, or something like that. And of course we could use a special case of C for Circle in place of however we'd specify p for circles (akin to how we use the special case of O for Octave in place of 2).
- But here's where I think you and I would differ. If I understand your thinking correctly, then I expect you'd say that we should only use n-LFSp, including for the primary use case of circles: n-LFSC. On the other hand, I'd say that we should use n-CSC for Center Sets of Circles, and only revert to n-LFSp when experimenting with these more complex ellipses and their foci. Your problem with my n-CSC acronym would be twofold:
- It contains a redundancy, because if we know we're using circles, then we already know their lower foci are their centers, so you think it's forbiddingly wasteful or confusing to say so.
- It makes the naming system overall more complex, because we have two acronyms where we could get away with only one.
- But I would counterargue:
- Redundancy isn't good, I agree, but having some is not a deal-breaker. "Center" conveys much more than simply "circleness", and "circle" conveys much more than simply "centerness"; it's well worth the slight amount of overlap in their meanings for us to convey the full implications of both.
- It's more important to give the primary use casers the clearest, simplest acronym, and let the experimenters deal with how to work around it. It's Dave's and my "don't FUSS" principle: don't foul up the simple stuff. In other words, what's more important than the simplicity of the system itself is the utilitarian simplicity of the average users' experience of the system. I accept the risk of n-CSp where someone mistakenly uses "centers" to refer to non-circular ellipses; that may confuse some of the advanced people, but that's on them; it doesn't bother me because it's not endangering the 99% of basic users who are doing the simple stuff with circles.
- But here's where I think you and I would differ. If I understand your thinking correctly, then I expect you'd say that we should only use n-LFSp, including for the primary use case of circles: n-LFSC. On the other hand, I'd say that we should use n-CSC for Center Sets of Circles, and only revert to n-LFSp when experimenting with these more complex ellipses and their foci. Your problem with my n-CSC acronym would be twofold:
- So if 99% of people have been coming here to deal with and talk about circle centers — and don't have any interest in the fact that these circle centers are also lower foci, which is a more advanced concept — then n-CSC is the more appropriate acronym. And I'm saying that this is analogous to people coming here to deal with overtone-based tunings, which a very basic music concept — and having no particular interest or awareness about their steps being equal frequency amounts, which is a more advanced physics/math concept. This is why I co-designed the naming system which offers n-ODp for the ordinary musician interested in otonalities, and n-EFDp for the more advanced experimenters. --Cmloegcmluin (talk) 19:58, 1 April 2023 (UTC)
(I'm resetting the indentation here. Hope that's okay.)
Initial apology
Hi, Flora. I should begin with an apology. I have been complaining that you interpreted "arithmetic" in a different sense than Shaahin originally intended. While I still believe it's clear that Shaahin intended the meaning as in "arithmetic progression", and that you mean it as in "arithmetic mean", I can now see that these are essentially the same meaning, because the principles that relate one step to the next in an arithmetic progression are the same which relate the value between two adjacent steps via the arithmetic mean (and the same point about the connection between progressions and means can be said about geometric progressions/means, and harmonic progressions/means). Almost certainly you have attempted to convey this idea to me and others in the past weeks, and probably some people got it right away, but it took a while to penetrate my thick skull. I'm very sorry about that. Perhaps I was blinded by confusion on account of that issue where there were two different senses in which we were using the word "sequence"; we recently agreed to use "progression" for the first kind, as in the "arithmetic progressions" I've spent this paragraph dealing with, and "sequence" for the other kind, as in the sequences (open-ended) vs. divisions (periodic) distinction used in the naming system I co-designed.
And so, I can see that you, in fact, have not distorted or abused Shaahin's original thinking at all, as I originally argued. The truth is the other way around. Of the two of us, it is you who are properly extending Shaahin's intentions when he coined "ADO". Both you and my team use "arithmetic" in the same way he does, but on two other points, you go with Shaahin, while my team went against. I have already acknowledged these two other points above, but I'll repeat them here:
- You've accepted his assumption of frequency as the default musical resource from which to make an arithmetic progression from / take arithmetic means of. We did not.
- You've accepted his association of "divisions" with "arithmetic". We did not.
So I recognize that some recent edits I made to the ADO and IDO pages should be revised. Also, I retract my suggestion that your acronyms be forced to include 'M' for mean, as in AMDO and IMDO; I can now see that this is unnecessary, confusing, and doesn't solve my main problem with your system anyway. Sorry again.
ADO should not be extended
And so now I can come to my point. My primary concern is not whether or not you've properly extended Shaahin's concept. My concern is that Shaahin's concept should not have been extended. In particular, I believe the first of the two design choices Shaahin made — which your ADO/IDO system is perpetuating — is dangerously confusing. It's this first choice, i.e. assuming frequency, which is the major problem; the second choice, i.e. "arithmetic divisions', in minor in comparison. I will be spending most of my time in this post addressing the problem with this first choice.
In support of my argument, I conducted some research. I searched through available archives of public discussion of xenharmonic topics for all relevant occurrences of the word "arithmetic", and gathered over 200 of these. My sources included the Mills tuning list, Yahoo Groups!, Facebook, and Discord. My oldest datum is from 1995; I did not include results that were more recent than 1 year old, and I also avoided unfairly including results that were explicitly about the system that Paul, Billy, and I designed. My goal was to understand how people in the community since the internet age began have most frequency used this word when describing tunings or scales. Along the way, I learned a lot about the pre-internet historical usage of the term as well.
Here's a key piece of information. Perhaps you understood this already. This was news to me. Originally, "arithmetic" was understood to refer to string length, not to frequency as Shaahin and yourself are doing. The concept of frequency — the period of vibrations in air — was not known to the ancient Greeks. The resource that was immediately visually able to be apprehended by them was the length of the vibrating string. This is why we experience confusion today where the harmonic mean relates frequencies of a subharmonic series rather than the harmonic series: ever since the discovery of frequency, it has been more intuitive for us modern thinkers to reason about frequency ratios like 2:3, 4:5, etc than it is for us to reason about wavelengths. But to the ancient Greeks, who thought in lengths, it was the overtones which were related by the harmonic mean, and it the undertones that were related by the arithmetic mean. If one checks the work of Zarlino, Marchetto, Schlesinger, Partch, and probably many others, this assumption that "arithmetic" refers to subharmonic relationships is perpetuated. For example, here's a quote from p69 of Genesis of a Music, where Partch defines the "Arithmetical Proportion":
an ancient principle of scale structure by which a sounding body is divided into a number of exactly equal parts, and a scale constructed from the resulting relationships, or ratios; this does not produce equal scale steps. The Arithmetical Proportion has been seized upon by some theorists as the ancient substantiation of "minor tonality", since, starting with the one part that gives the highest tone, it results in a series of tones the exact reverse of a fundamental and its series of partials, down to an arbitrary low tone determined by the number of equal parts used (see page 174). The Arithmetical Proportion may be considered as a demonstration of Utonality ("minor tonality").
However, my research shows that since the internet era, we find about a 50/50 split between statements where people assume "arithmetic" refers to string length per the historical usage, and statements assuming frequency per modern intuition. Notably, however, when we break the data down by unique individuals, we find many many more individual people who assume "arithmetic" referring to frequency than we do those who assume it referring to length. In other words, we have a small but very vocal minority of people who continue to use "arithmetic" in the original sense — most prominently Margo Schulter — and a large but scattered majority of non-experts (such as Shaahin Mohajeri, Bill Wesley, Paul Hjelmstad, Joakim Bang Larsen) who come to the table thinking of frequency ratios like 8:9 and 9:10 and take the arithmetic means of those, i.e. casually assuming frequency.
If you want to view the research, it's available here: https://docs.google.com/spreadsheets/d/1wUhccKnyobJIQf3Ra1wQ7amYSMlV-VVmV5FFnyHLrnQ/edit?usp=sharing This link includes the raw data, links, and several charts you may find interesting.
My conclusion is that it is unwise to propagate a system which assumes "arithmetic" referring either to length or to frequency. This is why Paul has been explicit about which resource he is sequencing arithmetically, using "arithmetic frequency sequence" since at least as far back as 2017, and why when Billy and I got together with Paul to codify and complete his design on the wiki in 2021, we maintained this approach.
Shaahin's term "ADO" is fine as a one-off personal name he would use for his compositions, but it is not acceptable as a term we should propagate in the community. (By the way, until you came to the problem recently, my research shows that ADO had very little traction in the community; only two other people besides Shaahin himself — and also you and CompactStar, of course — have claimed to use it. To be fair, I only found three other people adopting the system designed by Paul, Billy, and I. So it's a total of 5 people versus 6 people. Which is hardly a statistically significant difference.) It encourages the sort of problematic writings I've called out recently from CompactStar, who is taking the existence of ADO (and especially your propagation of it) as a sign that they can treat "arithmetic" as evoking frequency (e.g. in Arithmetic MOS scale or Arithmetic interval chain), despite the fact that for educated microtonalists that word implies the exact opposite thing: length. And so I can not accept "IDO" either, since it has the same deal-breaker of a problem.
Shaahin's (and your) approach are comparable to if Paul, Billy, and I had decided to write up FS, PS, and LS — frequency sequences, pitch sequences, and length sequences. Maybe some people would assume we meant arithmetic sequences, but what some people assumed harmonic sequences, or geometric sequences? It's just not safe to be less than fully explicit in this domain.
Fixing IDO; make it IFDO
As stated previously, however, I do believe that there is some value in the generalization of this idea to any power mean; this allows your system to cover ground which our system does not cover. And so, I don't recommend we completely reject it yet.
However, in order for your system to not be forbiddingly confusing, it must be modified to be explicit about the resource divided or sequenced, like our system does. So, your system must be changed at least from ADO to AFDO, and from IDO to IFDO. To be clear, I think it's clear from my research that you must explicitly include "frequency" in the name, or you'll be doomed to conflict and confusion.
In fact, I even came across some concerns about how EDO does not explicitly specify the divided resource: https://discord.com/channels/332357996569034752/780300193110818826/861278258350784522 "I think it'd be a good idea to clarify that the equal divisions are of log(frequency)". This agrees with Paul/Bill/I's decision to treat EDO as short for EPDO, where pitch of course = log(freq).
Of course, EDO is not the same as EFDO (it is the same as EPDO), but you could use GFDO, for geometric frequency division of the octave.
Here's a series of tables that will show the relationship between the three musical resources — frequency, pitch, and length — and the three key mathematical means/progressions — arithmetic, geometric, and harmonic — and how our two systems approach the space differently. Here's a part of the system I designed with Paul and Billy:
| frequency | pitch | length | |
|---|---|---|---|
| arithmetic (p = 1) | AFS | APS | ALS |
| geometric (p = 0) | (unused) | (unused) | (of low interest) |
| harmonic → "inverse-arithmetic" (p = -1) | (unused) | (of low interest) | (of low interest) |
And then here's your system:
| frequency | pitch | length | |
|---|---|---|---|
| arithmetic (p = 1) | ADO | (unused/unusable) | (unused/unusable) |
| geometric (p = 0) | (EDO) | (unused/unusable) | (of low interest) |
| harmonic → "inverse-arithmetic" (p = -1) | IDO | (of low interest) | (of low interest) |
This isn't a very direct comparison, since your system so far only deals with octaves, and deals with divisions rather than sequences. My main point here is conveyed by the coloration pattern, which runs diagonally across this space. Cells with the same color describe the same type of tuning phenomenon, but in different ways. But if your system was made unproblematic by being made explicit that it deals with frequency, and then extended to sequences and generalized beyond octaves for a more direct comparison with our system, then this is what it would look like:
| frequency | pitch | length | |
|---|---|---|---|
| arithmetic (p = 1) | AFS | (unused) | (unused) |
| geometric (p = 0) | GFS | (unused) | (of low interest) |
| harmonic → "inverse-arithmetic" (p = -1) | IFS | (of low interest) | (of low interest) |
Note at this point that we both agree on AFS in the blue top-left corner, for arithmetic frequency sequence. So we could actually combine our systems. Here's how that would look like:
| frequency | pitch | length | |
|---|---|---|---|
| arithmetic (p = 1) | AFS | APS | ALS |
| geometric (p = 0) | GFS | GPS | (of low interest) |
| harmonic → "inverse-arithmetic" (p = -1) | IFS | (of low interest) | (of low interest) |
I also completed the chart by filling in the last remaining viable cell: GPS in the middle for geometric pitch sequence.
Looking at this completed chart, we can see that another term for an arithmetic pitch sequence (e.g. something like Carlos alpha, beta, or gamma), such as how a user of our system would think of things, would be a geometric frequency sequence in your system; APS = GFS. And similarly, ALS = GPS = HFS (the last of which is to say, that a subharmonic series could be understood as a harmonic sequence of frequencies).
And so now we need to take a look at what makes your system have potentially new value, because my criticisms I shared with Fredg999 above still hold, i.e. I think it's clear that the system I co-designed is not only the unambiguous system that theorists need here, but also the more accessible system for music makers. But your system has one advantage, which is that it can cover theoretical space that our system cannot. It's the space between the three rows of this table, and beyond it:
| frequency | pitch | length | |
|---|---|---|---|
| super-arithmetic (p > 1) | pFS | pPS | pLS |
| arithmetic (p = 1) | AFS | APS | ALS |
| super-geometric (1 > p > 0) | pFS | pPS | pLS |
| geometric (p = 0) | GFS | GPS | (of low interest) |
| sub-geometric (0 > p > -1) | pFS | pPS | pLS |
| harmonic → "inverse-arithmetic" (p = -1) | IFS | (of low interest) | (of low interest) |
| sub-inverse-arithmetic (-1 > p) | pFS | pPS | pLS |
By the way, these terms "super-arithmetic", "sub-geometric", etc. are not well-thought-out coinages. Just needed to fill out the table.
And also, I note that as far as I know, there's no particular reason to be interested in these spaces. That's why I used the term "potential" above. It's the only reason I don't ask you to completely remove IDO (or IFDO) from the wiki entirely.
Finally, I note that CompactStar's RMS-based tuning proposed on Discord which got this discussion kicked off would be a 2FDO.
Is it even safe for Paul, Billy, and I to use "arithmetic" at all?
I think there's one big remaining question here, and that's whether — given how problematic the word "arithmetic" is — is it okay that Paul's/Billy's/my system uses it at all? That is, while Margo is someone who consistently assumes arithmetic to refer to string length, she is also open to applying the term arithmetic to frequency or pitch when it is made explicit. But will everyone like her who assumes arithmetic defaults to length be open to it applying to other resources?
My answer is: I'm not sure, but I think so. In any case, we can't allow ancient historical usage to block effective modern usage. So I contend that the page I created for Arithmetic tunings is still acceptable, on the grounds that it uses "arithmetic" in the way it actually means: referring to arithmetic means or sequences/progressions as applied to musical scales or tunings. That said, I should certainly at least add some historical notes along the lines of the stuff I reported here from my research.
As a thought experiment, though, what if we decided that "arithmetic" was irredeemably tainted with confusion, and dismissed it entirely? What would the page "arithmetic tunings" be instead, then? Well, almost certainly it would be "equal-step tunings". However, there is already a page with that name, where it doesn't quite mean the same thing. The existing Equal-step tuning page assumes pitch as the default resource, whereas I would be here wanting it to be general to frequency and length too. This would begin to necessitate a major overhaul, along the lines of insisting that the existing equal-step tuning page be changed to equal-cents or something like that. There is a precedent in "equal-hertz" which is an old, outdated term for "isoharmonic", and we could then have "equal-wavelength" to complete the set. But anyway, I don't think such an overhaul is reasonable, nor am I interested in dealing with such a thing anyway.
Conclusion
So I'll try to come to a concluding statement now. I don't particularly care if you do choose to extend your system from divisions to sequences. Or if you generalize it beyond octaves. But I insist that you leave Shaahin's work alone and do not try to extend it. It was never designed to be coherent and comprehensive in the way folks like you and me want systems to be. If you do still believe it is of theoretical interest to think of and explore tunings described by various power progressions of frequencies, then by all means do so, but please recognize the historical danger involved using the word "arithmetic" unqualified, and I strongly recommend that you and CompactStar take all the recent explosion of stuff you created with ADOs and IDOs and change them to AFDOs and IFDOs, please. This is a big opportunity to get the community educated on the relationship between these three progressions and these three musical resources. I can't describe how disheartening it was for me during my week of research to see the same confusion playing out over and over and over and over and over again when people would use "arithmetic" without being explicit about with regards to what. I don't want to leave future impressionable newcomers like CompactStar vulnerable to conflating columns of the tables in this post with their rows.
The rest of the stuff in this post is just supporting information.
Paul's explanations
Here are some samples of Paul's explanations over the past 20 years or so, about the confusion inherent in the situation:
2002
https://yahootuninggroupsultimatebackup.github.io/harmonic_entropy/topicId_581#584
the arithmetic progression of the frequencies in the harmonic series? that would make sense, but unfortunately you have to be careful around tuning folks -- 'arithmetic', as opposed to 'harmonic', divisions of intervals historically refer to the arithmetic division of a string, which result in a *subharmonic*, rather than a *harmonic*, series.
2002
https://yahootuninggroupsultimatebackup.github.io/tuning/topicId_39746#39926
in the old days, before the physical harmonic series was known (a natural phenomenon in which any tone tends to be accompanied by tones with integer multiples of its FREQUENCY), string lengths on monochords were used to compare pitches, and many theorists demanded simple proportions in those string lengths. string length is approximately inversely proportional to frequency. if these string-length proportions were ARITHMETIC (that is, in proportions belonging to the series 1, 2, 3, 4, 5 . . .), the result was what is today known as SUBHARMONIC. if these proportions were HARMONIC (that is, in proportions belonging to the series 1/1, 1/2, 1/3, 1/4, 1/5 . . .), the result was what is today still known as HARMONIC (though typically expressed today as a set of ARITHMETIC proportions in FREQUENCY).
2003
https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_8130#8160
The reason for this is historical. We say whole number multiples today because everyone since Fourier talks about frequency measurements. In the old days, it was string length measurements (or still today, period or wavelength) where the numbers are *inversely proportional* to the frequency numbers. So the harmonic series in the old days *was* 1/1, 1/2, 1/3, 1/4, etc, and yet it's the same harmonic series that today goes 1, 2, 3, 4 . . .
2019
https://www.facebook.com/groups/untwelve/posts/2447957548592730/?comment_id=2453839764671175
[Arithmetic Division of the Octave] could mean several different things. Prior to the 17th century, it would typically have meant a Utonal series. More recently, it would typically mean an Otonal series. One can reckon pitches in different ways and what is "arithmetic" one way is not arithmetic in the other ways.
2019
https://www.facebook.com/groups/xenharmonicmath/posts/1536904806449736/?comment_id=1536991326441084
Janne Karimäki:
The name of such scales is ADO, meaning arithmetic division of the octave. You have 5-ADO, 10-ADO, and so on there.
Paul Erlich:
Careful because "arithmetic" typically means Utonal while this scale is "harmonic" or Otonal. I've only ever seen one person use the ADO moniker and it's caused a lot of confusion.
Janne Karimäki:
It makes perfect sense to me.
Paul Erlich:
The Arithmetic Proportion or Arithmetic Division usually refers us subharmonic aka Utonal series, not harmonic series. That's because the terminology originates in antiquity, prior to the scientific revolution, and string lengths were still used to reckon pitches.
Janne Karimäki:
There is also the name EDL, equal division of length, which directly applies to strings.
Paul Erlich:
True but without context of that "opposite", the preponderance of conflicting terminology out there tends to confuse a few people every time.
2020
Paul Erlich:
Steve, that may have been true prior to the 17th century, when the nature of pitch as rapid vibration was not yet known, and string lengths were used to reckon and describe scales, but today musical divisions are reckoned according to frequency, so 4:5:6 becomes the arithmetic mean division and 10:12:15 becomes the harmonic mean division, as Joakim has said. What is confusing is that the etymology comes from prior to the 17th century, so what we call the "harmonic series" today is named after how it looks with respect to string divisions, even though the harmonic series is an arithmetic progression in modern (frequency-based) terms.
Margo Schulter:
Paul, I agree that how one approaches this depends on what sources one follows; and to me, the 17th century is rather ultramodern, so that I follow the more traditional terminology. But it's a traditional view that the harmonic division (as defined by string lengths) is indeed the most harmonious for vertical sonorities. Thus _Cpmpendium de musica_ (c. 1350?) argues that the fifth is best placed below the fourth in a three-voice sonority dividing the octave because there is a natural series of numbers 2-3-4 (with the 3:2 fifth preceding the 4:3 fourth). This source also gives what might be called the quaternario or series 1-2-3-4, in which 2-3-4 is concluded (with the 1-2-3 sonority, an octave plus an upper fifth forming a 12th above the lowest voice, also a common 14th-century close). Zarlino likewise uses the senario, 1-2-3-4-5-6, to demonstrate that the division of the fifth where the major third precedes the minor third is more harmonious and "joyful." So the conclusions of these sources fit the later concept of the harmonic series.
As a bonus, here's another great statement I found from Tony Durham, in 2021:
One reason why the nomenclature is confused: it depends whether you are thinking in terms of frequency, wavelength or subjective pitch. Harry Partch built acoustic instruments. He thought in wavelengths, so it was natural for him to describe Utonal sequences as arithmetic. But somebody who works in electronics, and thinks in frequencies, is more likely to describe the overtone sequence as arithmetic. Each is right in its way. I've tried to summarise this in a table. Feedback welcome: I didn't spend long on this and it is probably far from perfect.
More background information on Shaahin's and our ideas
As I've pointed out earlier, Shaahin's work is clearly not striving toward a coherent system that fits into existing practice as smoothly as possible (as Paul, Billy, and I did). Or at least, if this was his intention, he failed quite badly at it.
I note that for him it was not simply ADO and EDL. He also had ARDO, ARD, AID, and ADL. I have given up on trying to understand the relationship between all of these things. But if you'd like to try to make sense of it, a lot of the links he's shared on Facebook and Yahoo Groups! are dead now, but I found them on the Internet Archive's Wayback Machine, so you can explore yourself:
https://web.archive.org/web/20210612173344/http://www.96edo.com/Sometuningmodels.html
We found it particularly frustrating that he acknowledged his A(R)DO as a otonal system, but did not leverage that terminology, instead, unnecessarily coining something new.
I haven't gone back and re-read these recently, but I recognize these as the two main discussions where Paul, Billy, and I developed our system, if these might be of interest here:
https://www.facebook.com/groups/xenharmonic2/posts/4023222704364668
https://www.facebook.com/groups/497105067092502/permalink/1980938532042474/
--Cmloegcmluin (talk) 22:52, 8 April 2023 (UTC)
Additional thoughts
Okay, sorry for how lengthy my side of this thread is getting. But I had some further thoughts overnight. I'll try to keep it brief.
The page I created for Arithmetic tunings is like the first row of the tables I shared above. Like this:
| frequency | pitch | length | |
|---|---|---|---|
| arithmetic (p = 1) | AFS, OS, EFD, OD | APS, AS, E(P)D | ALS, US, ELD, UD |
While your system is like the first column. If you created a central page for them, it'd be called Frequency sequences. Again, we overlap on the top-left cell, for AFS. Like this:
| frequency | |
|---|---|
| super-arithmetic (p > 1) | pFS, pFD |
| arithmetic (p = 1) | AFS, AFD |
| super-geometric (1 > p > 0) | pFS, pFD |
| geometric (p = 0) | GFS |
| sub-geometric (0 > p > -1) | pFS, pFD |
| harmonic → "inverse-arithmetic" (p = -1) | IFS, IFD |
| sub-inverse-arithmetic (-1 > p) | pFS, pFD |
There's no reason to worry about the middle of the table, i.e. where I had "GPS" for "geometric pitch sequence". Because of the diagonal equivalence pattern, it's only necessary to think in terms of possible arithmetic sequences (our system), or possible frequency sequences (your system).
These two systems have reason to coexist. For some people, our system may make more sense. For others, yours may make more sense. Though I repeat, that I think our system is more natural for actual musicians, while yours may be more natural for mathematicians or engineers.
A vs E
But what my system calls an "EFD", for "equal frequency division", yours calls an "AFD", for "arithmetic frequency division". Per Talk:Arithmetic tuning, Paul, Mike, and I find "arithmetic division" incorrect and prefer "equal division".
But it's not a simple fix for your system, because you're not really speaking about dividing arithmetically, which doesn't make grammatical sense, and that's our concern; you're talking about dividing with respect to the arithmetic mean/progression. Before I understood the relationship between means and progressions, I had suggested "arithmetic-mean-based division", but you noted that your system is as much about progressions as it is about means, and I see that now.
But I do have an observation which might help with this. Since the main new value for your system is how it can fill in between and beyond the values of p = 1, 0, and -1, it's really about power means. And I don't find that "power progressions" are written about much, so I believe that "mean" should take precedence over "progression" here. In other words, I suggest that your system might even better be thought of as the "frequency power mean sequence" system, and indeed AFD would stand for "arithmetic-mean-based frequency division".
Nonetheless, perhaps "frequency power progression tunings" or something like that, with AFD standing for "arithmetic-progression-based frequency division". Not sure. Just suggestions.
--Cmloegcmluin (talk) 18:15, 9 April 2023 (UTC)
I have not been following your discussion with Flora, but from what I've gathered, you believe that your system using the terms EFDO and ELDO is more intuitive for musicians due to naming resources frequency and length, whereas my/Flora's system using ADO and IDO is more generalizable. However, there is an easy way to have both of these advantages–use a spectrum of resources rather than means, where the "n-resource" is expressed in terms of frequency as fn. The terms EFDO, ELDO, and E(P)DO can be maintained for n = 1, n = -1, and n → 0 respectively. For any other p, the term "EnDO" (equal n-resource division of the octave) can be used, so the tuning I described on Discord can be called an E2DO, and the tuning halfway between EDO and EFDO can be called an E0.5DO.
CompactStar (talk) 01:00, 10 April 2023 (UTC)
- Hi CompactStar. Yes, you've gathered correctly; that is a big part of what I'm saying: that my team's system is more accessible, while yours is capable of generalizing to unexplored theoretical territory. (The other biggest part is that due to historical and contemporary usage patterns, "ADO" is unacceptable in a tuning name system.) Now, I do like how you're thinking here, attempting to synthesize the strengths of our two systems. I had not really thought of trying something like this. But unfortunately, I don't think I would recommend we go with this particular suggestion of yours. I wish I liked it... I really don't want to come across as inflexible or overly negative here. My problem is this: there's just no direct association of these resources — frequency, pitch, and length — with those numbers — 1, 0, and -1. In other words, in order to understand why a E(0.5)DO referred to a tuning between an EFDO and an EDO, one would have to understand several things:
- arithmetic/geometric/harmonic progressions in the first place,
- and then understand the blue/red/yellow "diagonal" relationship between frequency/pitch/length and arithmetic/geometric/harmonic progressions (that I showed off in the tables above),
- and then understand the relationship between such progressions and the associated means,
- and then understand how those famous means with special names (arithmetic, geometric, harmonic) generalize as power means (where p = 1, 0, -1, respectively).
- So if we're going to discuss 0.5 tunings like this, I think we might as well use a more immediate and clear approach to it, as in the ... 2FDO, AFDO, (0.5)FDO, GFDO, (-0.5)FDO, IFDO, (-2)FDO ... continuum. If people are using this system already (i.e. your system, as revised according to my suggestions), then they should already know point #1, and possibly #3 too; it's really point #4 that's the interesting new thing. The key thing is they would never need to understand point #2. And this likens back to why I think our systems can coexist; because someone who thinks primarily in terms of frequency ratios like 7/6, 5/4, 3/1 etc. as well as in terms of these power means, well, they may potentially never have to learn anything about the "diagonal" relationship with pitch and string length (and vice versa, someone like me, for whom thinking about frequency, pitch, and length came naturally, would never have to learn about geometric and harmonic means, which indeed I had gotten away with my whole life without understanding, that is, of course, up until this whole issue came up earlier this year!) --Cmloegcmluin (talk) 03:20, 10 April 2023 (UTC)
- I agree with most of what Cmloegcmluin said so far, especially about the importance of keeping both the type of sequence and the type of resource clearly identified. However, I'm not certain that the equivalences presented in the tables above using colour coding are all exact. This is related to Cmloegcmluin's remark that "there's just no direct association of these resources — frequency, pitch, and length — with those numbers — 1, 0, and -1"; there is an association, but it is indirect, and that may lead to misconceptions. Let's dive right in!
- Frequency: An AFSp is currently defined as [math]\displaystyle{ f_{\text{AFS}}(k) = 1 + k \cdot p }[/math], which means that step [math]\displaystyle{ k }[/math] in the sequence has frequency [math]\displaystyle{ f(k) }[/math]. It is odd that this function outputs a pure number, since frequency is not a pure number, being usually expressed in Hz. Therefore this function doesn't really give the frequency, but rather the frequency ratio associated with step 0 of the scale. That is not a trivial step: it implies that the "natural" way to relate pitches to each other (i.e. intervals) is through frequency ratios, even though the purpose of this system is to avoid taking any of these things for granted! So, for the purposes of this discussion, let me redefine the function as follows: [math]\displaystyle{ f_{\text{AFS}}(k) = f_0(1 + k \cdot p) }[/math], where [math]\displaystyle{ f_0 }[/math] is the frequency of step 0, in Hz. To explain CompactStar's point, let me again rewrite the function: [math]\displaystyle{ f_{\text{AFS}}(k) = f_0(1 + k \cdot p)^1 }[/math]. The reason for the added exponent 1 will be clearer in the next steps.
- Length: I'll skip over pitch for reasons that will be clearer later. An ALSp is currently defined as [math]\displaystyle{ L_{\text{ALS}}(k) = 1 + k \cdot p }[/math]. Again, to make sure that the function properly outputs a length, we'll need a length constant. Here is a first modified version of the function: [math]\displaystyle{ L_{\text{ALS}}(k) = L_0(1 + k \cdot p) }[/math], where [math]\displaystyle{ L_0 }[/math] is the length associated with step 0 of the scale. With this settled, we already see that we will need some work to compare both functions in terms of frequency, so we need to know the relationship between length and frequency. As usual in math, relationships are easier to find with some sort of constant, and what we need here is the speed of sound. (Of course, it isn't technically a constant, but we're not diving into underwater music discussions today!) The speed of sound is equal to the multiplication of wavelength by frequency. To make this more obvious, notice that length is usually expressed in m (meters), while frequency is usually expressed in Hz, which is equivalent to s−1, and finally the speed of sound is usually expressed in m/s (or m·s−1), i.e. the multiplication of the previous two units. As a formula, it looks like this: [math]\displaystyle{ c = {\lambda}f }[/math], or [math]\displaystyle{ f = \frac{c}{\lambda} }[/math], where [math]\displaystyle{ c }[/math] is the speed of sound. Now, string/tube length and wavelength are not the same property, so we have to make sure that they are proportional before we can proceed in our reasoning. We can discuss this if it becomes an issue, but for now I believe we can assume confidently that wavelength and string/tube length are proportional (e.g. twice the string length implies twice the wavelength, which is associated with half the frequency if the speed of sound is constant). Therefore, string/tube length can be derived from wavelength using a pure number constant, knowning that it inputs a length and outputs another length. That new constant largely depends on the physicality of the instrument (shape, material, etc.), and to avoid getting in the physics of strings and tubes, we'll just define [math]\displaystyle{ m = \frac{\lambda}{L} }[/math] ([math]\displaystyle{ m }[/math] for "material", and I'm carefully avoiding [math]\displaystyle{ \mu }[/math] which is often used in string physics equations), such that multiplying by [math]\displaystyle{ m }[/math] inputs a string length and outputs the corresponding wavelength. Let's see how our function looks like through the lens of frequency: taking this step by step, we first have [math]\displaystyle{ \lambda_{\text{ALS}}(k) = m \cdot L_0(1 + k \cdot p) }[/math], and then [math]\displaystyle{ f_{\text{ALS}}(k) = \frac{c}{m \cdot L_0(1 + k \cdot p)} }[/math]. That last formula doesn't look very good with the big fraction, so let's clean it up a bit: [math]\displaystyle{ f_{\text{ALS}}(k) = \frac{c}{m \cdot L_0} (1 + k \cdot p)^{-1} }[/math]. The fraction now holds only the constants, which are equivalent to [math]\displaystyle{ f_0 }[/math], and we notice that the [math]\displaystyle{ (1 + k \cdot p) }[/math] bit is now written using an exponent −1. This should make it clear why I added a seemingly useless exponent 1 in the AFS function earlier, and why CompactStar is proposing to use −1 for ELDO/ALS. That said, the constants seem nontrivial to me, because they can become variables if you open up to creating new scales instead of just observing a single scale from different angles, and so this can help showcase a few different approaches to creating scales.
- Pitch: We're getting to the good part now. An APSp is currently defined as [math]\displaystyle{ P_{\text{APS}}(k) = k \cdot p }[/math]. The absence of the [math]\displaystyle{ 1 + }[/math] in this formula should already alert us that something is different about this sequence compared to the previous two. As we know, pitch perception is mostly logarithmic, and while there are complicated functions that try to show precisely how the human ear perceives pitch, most xenharmonists are used to simply take a logarithmic ratio of frequencies, commonly expressed in cents, a dimensionless unit, making pitch a pure number: [math]\displaystyle{ P = \log_b \left(\frac{f}{f_0}\right) }[/math]. It is important to note that you cannot take the logarithm of a frequency, because the logarithm of the unit Hertz is not defined in any way that would meaningful to us. So whereas there is a relationship between frequency and length, there is no direct relationship between frequency and pitch, but only one between frequency ratio and pitch. So we'll need to carry [math]\displaystyle{ f_0 }[/math] with us now. We need the reciprocal of the previous formula to be able to express frequency as a function of pitch: [math]\displaystyle{ f = f_0 \cdot b^P }[/math]. We're ready to write our APS function in terms of frequency: [math]\displaystyle{ f_{\text{APS}}(k) = f_0 \cdot b^{k \cdot p} }[/math]. We can see very clearly that this function cannot be written using the same structure as the previous two functions but using an exponent 0 instead of 1 or −1, otherwise we would end up with a constant function.
- Let's check the colour coding. There is only one blue cell, so there's nothing to do here. The two red cells are APS and GFS. An APS is equivalent to any familiar equal-step tuning, and we know that each step of such a tuning has a constant frequency ratio, therefore the GFS checks out. Now, there are three yellow cells, so it might be a bit trickier. ALS and IFS are easy to check, because they're basically equivalent by definition: length and frequency are inversely proportional, and inverse-arithmetic is called that way for a reason. The actual tricky part is with GPS. Let's take ALS and GPS. I ran a quick example in a spreadsheet, only to find that the ratios between the pitches of each step of the ALS were not constant as one would expect from a geometric progression, but rather took the form of a decreasing sequence that converged to 1. We can see why that happened by working through our formulas. Let's recall our frequency-based ALS formula: [math]\displaystyle{ f_{\text{ALS}}(k) = f_0 (1 + k \cdot p)^{-1} }[/math]. Now, what does a GPS look like? Well, already in terms of pitch it should be something like this: [math]\displaystyle{ P_{\text{GPS}}(k) = P_0 \cdot p^k }[/math], for some constant [math]\displaystyle{ p }[/math] and starting pitch [math]\displaystyle{ P_0 }[/math]... Hang on, wouldn't [math]\displaystyle{ P_0 }[/math] just be 0? And multiplying anything by 0 results in 0? Clearly, something weird is happening here. To avoid this problem, let's rewrite the ALS in terms of pitch and check if it looks like a geometric progression: [math]\displaystyle{ P_{\text{ALS}}(k) = \log_b((1 + k \cdot p)^{-1}) }[/math]. This can be rewritten to get rid of the negative exponent using logarithm laws: [math]\displaystyle{ P_{\text{ALS}}(k) = -\log_b(1 + k \cdot p) }[/math]. This function shows that pitch decreases monotonically, diverging to negative infinity, but doing so more and more slowly, which explains why the ratios between consecutive pitches converged to 1. In a geometric pitch sequence with p < 1, you can get a decreasing sequence of pitches, but that sequence will converge to 0, which is different from the behaviour of an ALS. Clearly, GPS is doing something completely different from ALS/IFS, and that is mostly because of how logarithms work.
- Why 0 then? A good reason one might want to assign a value of 0 to pitch, placing it in between the 1 of frequency and the −1 of length, is by considering the derivatives of the frequency functions. Derivatives express how a function varies over its domain, which describes musically how the steps increase or decrease over its range, and typically taking a derivative of a polynomial brings the exponents down by 1. A special case is [math]\displaystyle{ \log_b(x) }[/math], whose derivative is [math]\displaystyle{ \frac{1}{x} }[/math], or [math]\displaystyle{ x^{-1} }[/math]. So even though pitch isn't [math]\displaystyle{ x^0 }[/math], if you consider its derivative to be [math]\displaystyle{ x^{-1} }[/math] and shift everything up by 1, then you get the index number 0. Similarly, the derivative of [math]\displaystyle{ x^{-1} }[/math] is [math]\displaystyle{ -x^{-2} }[/math], and disregarding the sign, you can see that the exponent went down by 1 again, so you can move it up by 1 and get the index number −1. The frequency case is basically the same, but without a sign change, and you find the index number 1.
- What's the takeaway? First, as I often say, it's always a good idea to carry the units around, and that could be improved on the individual pages for ALS and such. Second, I think we can learn some insight from the derivatives of the frequency functions, but we should check properly which scale structures are truly equivalent, especially if we're going to generalize this system to all power means and write on the Xen Wiki about it. The "diagonals" in the table aren't as simple as one would first expect, mostly because log spaces and linear spaces don't behave the same way, namely in terms of how they handle 0 and negative numbers, and making a continuous transition between both worlds isn't as simple as putting numbers in the middle and hoping it works out of the box. I don't think GPS is a well-defined structure at all, for that matter. It will be interesting to see what kinds of structures work and which ones don't, in terms of combining the horizontal "resource" axis with the vertical "power mean" axis. There might be other things to keep in mind, but I think it's important to at least make sure that linear/dimension-1 resources (those that have units with exponent 1, so length and frequency) remain strictly positive, while log resources (dimensionless, so pitch), can take any real value. It's also good to ponder what the units will look like: are the elements of an E(0.5)DO expressed in Hz0.5? Does that have any physical or psychoacoustic significance or is it purely recreational mathematics at this point? --Fredg999 (talk) 08:58, 10 April 2023 (UTC)
- Woa I'm really impressed by all the researches you guys have done here. Those tables are super helpful. You know, I vaguely felt the underlying structure but never tried to clear my mind or to even convey it. Anyway, to keep the convo short: I'm fully convinced that my terms need to be fixed, that ID must be IFD, that there's the equivalence of AP(D/S) and GF(D/S), and of AL(D/S) and IF(D/S). If I interpreted it correctly, Fred pointed out that GP(D/S) is different from AL(D/S)~IF(D/S), which makes sense to me.
- Dang, Fredg999, that's some good stuff! Yes, I did notice last week that some of the pages I made back in 2021 sorta take the units for granted, such as assuming frequency or length as the musical resource being sequenced or divided, just like how I'm warning against here. At the time I wrote those pages, I wasn't cognizant of all these historical usages and conceptual relationships, but now I certainly agree that this aspect needs fixing. (Also, I think my experience working with Dave on the RTT guide, where we ended up including an entire article on units analysis, has influenced me to appreciate and advocate for mindfulness of units too.)
- And Flora, I'm delighted and relieved to find that you basically agree with the main ideas I presented. I was afraid I'd been too harsh or impatient with you. As always, it's fun to confront these intellectual/musical/pedagogical challenges with you.
- Alright, so I figure that we should give Flora and CompactStar the first pass at updating the pages they created. To be clear, this is not because I consider it their responsibility or anything, nor because I want to create work for them to do; it's because I want to give them the opportunity to make their own pages (as well as Shaahin's original pages) as clear and coherent as they can according to their own thinking. Plus this'll be a good test of the new perspective Fredg999 and I brought to the problem, to see if other people besides us can articulate it well; I bet y'all can improve further upon how we explained things, by ironing out whatever idiosyncrasies to our approaches. I expect that after they take care of this, since we seem to be largely on the same page together now, while Fredg999 and I may have some comments or tweaks here or there, probably we won't need to have too much back and forth discussion after that.
- Meanwhile, I should do what I can to tighten up all the pages that I originally made. While I share credit for designing my system with Paul and Billy, they aren't hands-on with the wiki, so I can take care of it. That said, if Fredg999 wants to take the first pass themself — i.e. at updating the equations on the AFS, APS, and ALS pages per his comment above, like including the base frequency so as to return actual steps in frequencies rather than pure numbers — that's A-OK with me.
- Finally, I should acknowledge that Fredg999 is 100% right about the GPS issue. In other words, I still definitely stand by the relationships I described between the arithmetic row of the tables and the frequency column of the tables, but anything else I said about the cells anywhere in the middle of those tables wasn't as carefully thought out, and I can see now that it's incorrect. Thanks for taking the time and care to lay it out so clearly, Fredg999. Well...! But now I'm just fascinated by the questions you've raised w/r/t this "geometric pitch sequence" idea. If it is to be defined, I think it has to be defined in terms of intervals, not pitches (along the lines of how you showed that both [math]\displaystyle{ f }[/math] and [math]\displaystyle{ f_0 }[/math] must be included in pitch-related formulae); when describing scales in cents, we often start with 0¢, but that won't work if we want to repeatedly multiply it by something, of course... so we'd need to describe a scale that, say, starts with a 100¢ interval, then goes by 90¢, then by 81¢, then 72.9¢, etc. etc. I went to my harmonotonic tunings page because I thought I'd been pretty comprehensive about all step-monotonic tunings back when I wrote it, but as far as I can tell, scales like this are not documented yet at all. I hoped maybe this'd be equivalent to, like, some sort of a powharmonic series or logharmonic series, but I really don't think so. But anyway, that stuff's really not fresh in my head, and also I really shouldn't be spending too much of my time on these sorts of experiments, but I encourage y'all to go wild.
- First things first though... let's clean up what we've got out there already. Let me know if my plan basically makes sense to y'all too, or else I'll just keep an eye out for your changes to pages. --Cmloegcmluin (talk) 22:32, 10 April 2023 (UTC)
- Couple quick things.
- Previously I had requested that Flora and CompactStar's system be deprioritized relative to the one from me, Paul, and Billy, e.g. that the redirects should be altered so that AFDO redirects to ODO and on those pages the bold term ODO given first before AFDO, etc.; I no longer think this. If Flora and CompactStar are the ones exploring these tunings first, they should do it however they like. So I retract that request and apologize for making it before I understood the whole situation well enough.
- Also, I have some more info on GPS. Here's a table:
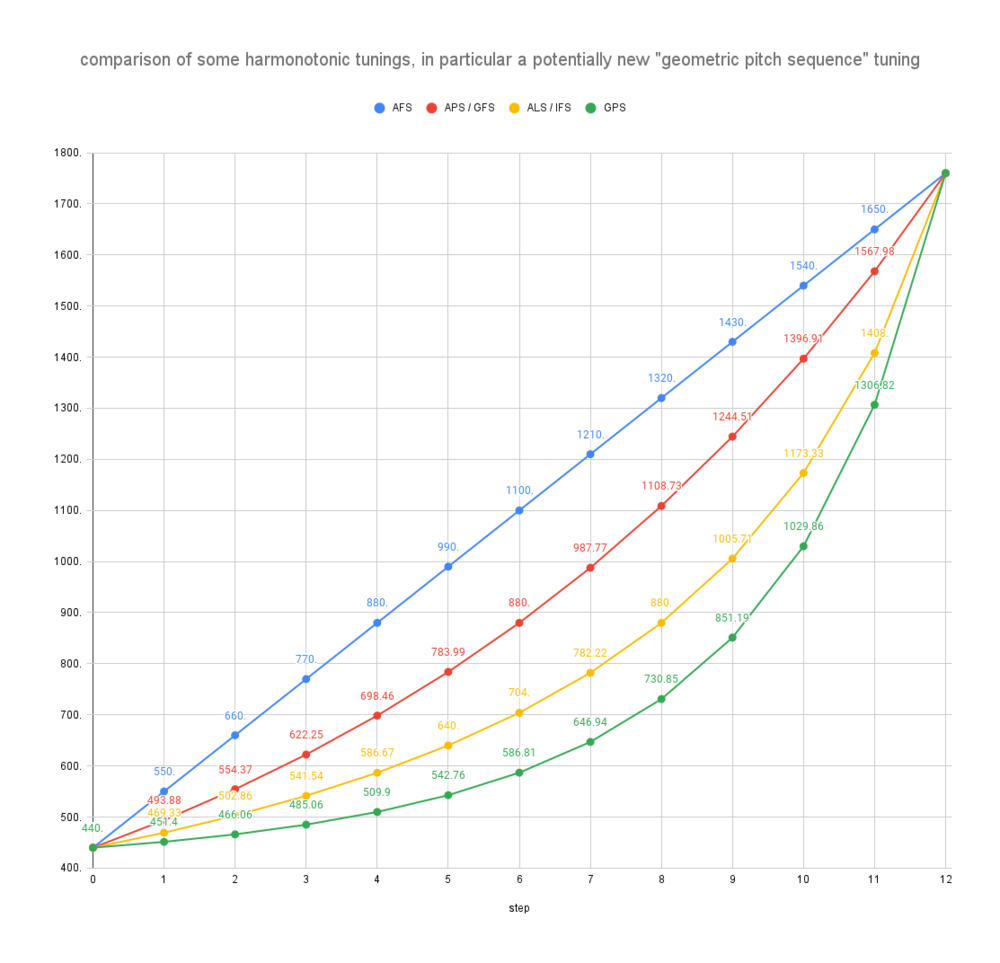
step AFS APS / GFS ALS / IFS GPS 0 440. 440. 440. 440. 1 550. 493.88 469.33 451.4 2 660. 554.37 502.86 466.06 3 770. 622.25 541.54 485.06 4 880. 698.46 586.67 509.9 5 990. 783.99 640. 542.76 6 1100. 880. 704. 586.81 7 1210. 987.77 782.22 646.94 8 1320. 1108.73 880. 730.85 9 1430. 1244.51 1005.71 851.19 10 1540. 1396.91 1173.33 1029.86 11 1650. 1567.98 1408. 1306.82 12 1760. 1760. 1760. 1760.
- And here's a chart of the same data:
- So it appears that GPS are on the other side yet of things from ALS/IFS. Please check my work. I couldn't find a direct formula for GPS in terms of [math]\displaystyle{ k }[/math] like I could for the other three. If you want to see my spreadsheet with formulas, let me know. --Cmloegcmluin (talk) 18:54, 11 April 2023 (UTC)
- Whoops, I meant to add a "Hz" label to the vertical axis in that previous chart.
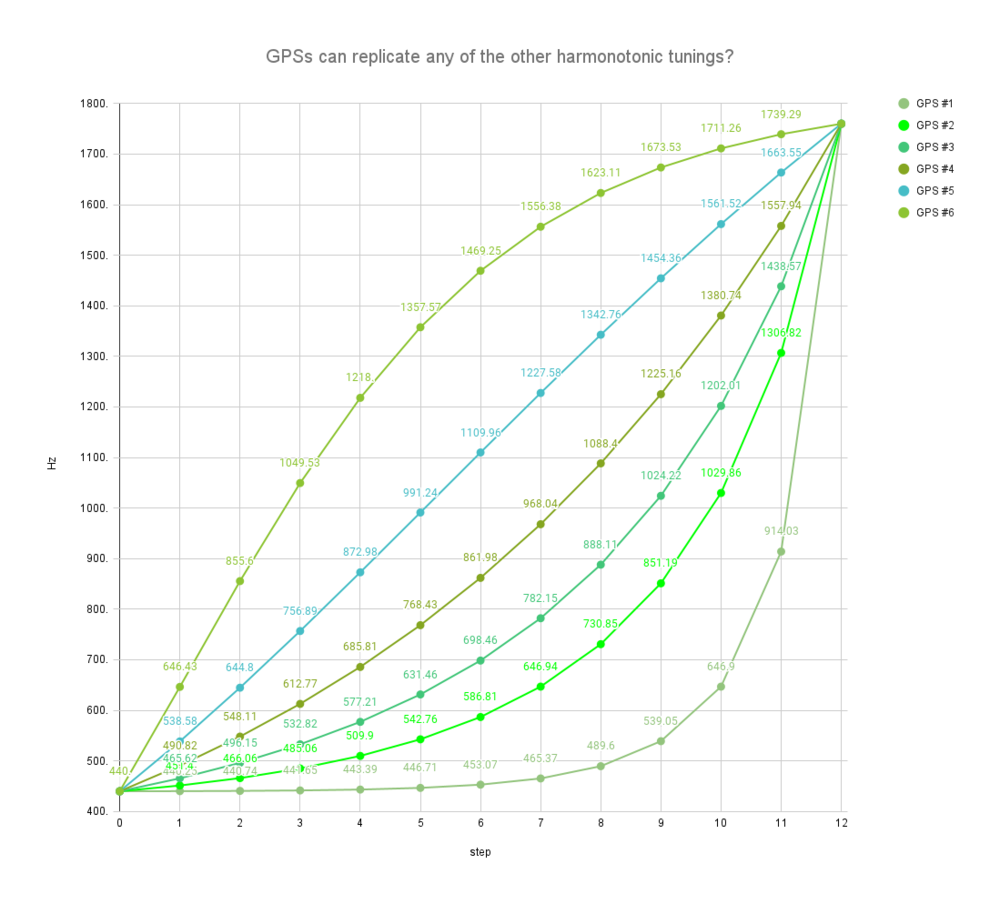
- Argh, I couldn't help myself from spending more time on this GPS thing. It occurred to me that while if you want to divide up some interval into [math]\displaystyle{ n }[/math] steps according to AF, AP/GF, or AL/IF, there is only one way to do so. However, if you want to do this for a GPS, there is a continuum of infinitely many possible ways to this, because you have two parameters to control: the initial step size (such as in cents), and the geometric factor by which it increases (or decreases) in size. The graph I shared above shows the only possible 12-EFD4/12-AFD4, 12-ED4/12-GFD4, and 12-ELD4/12-IFD4. But the 12-GPD4 I showed there is only one example of a 12-GPD4; a GPD or GPS requires more parameterization than [math]\displaystyle{ n }[/math] and [math]\displaystyle{ p }[/math] (the divided interval). It also needs one or the other of the initial step size or the geometric factor. I'm not sure which one would be more intuitive to ask people to provide. Given one, the other will be set (i.e. assuming you also already have [math]\displaystyle{ n }[/math] and [math]\displaystyle{ p }[/math]. Here's several more examples of 12-GPD4's. The one I gave in the previous graph is GPS #2 here. While in my previous post I stated GPS was on the other side yet of ALS from AFS, it looks like it may be possible to replicate any of the other harmotonic tunings. That said, I don't think it's actually possible to exactly recreate an AFS with a GPS... I can't quite tell, but it seems like maybe that nearly-straight line is actually a subtle S-curve, which I can't quite make sense of why it would be an S... anyone else got a bright idea?
- Maybe it was dumb not to show my work in the previous post. Here's the raw data for that chart:
GPS #1: initial step is 1 ¢, geometric factor is 1.90 GPS #2: initial step is 44.27 ¢, geometric factor is 1.25 GPS #3: initial step is 97.97 ¢, geometric factor is 1.12 GPS #4: initial step is 189.24 ¢, geometric factor is 1.01 GPS #5: initial step is 350 ¢, geometric factor is 0.89 GPS #6: initial step is 666 ¢, geometric factor is 0.73 step cents interval cents frequency ratio Hz cents interval cents frequency ratio Hz cents interval cents frequency ratio Hz cents interval cents frequency ratio Hz cents interval cents frequency ratio Hz cents interval cents frequency ratio Hz 0 0 440. 0 440. 0 440. 0 440. . 440. 0 440. 1. 1. 44.27 1.03 97.97 1.06 189.24 1.12 350. 1.22 666. 1.47 1 1. 440.25 44.27 451.4 97.97 465.62 189.24 490.82 350. 538.58 666. 646.43 1.9 1. 55.34 1.03 109.97 1.07 191.13 1.12 311.63 1.2 485.33 1.32 2 2.9 440.74 99.62 466.06 207.94 496.15 380.37 548.11 661.63 644.8 1151.33 855.6 3.59 1. 69.18 1.04 123.43 1.07 193.04 1.12 277.46 1.17 353.67 1.23 3 6.49 441.65 168.8 485.06 331.37 532.82 573.41 612.77 939.09 756.89 1505. 1049.53 6.81 1. 86.47 1.05 138.55 1.08 194.97 1.12 247.04 1.15 257.73 1.16 4 13.3 443.39 255.27 509.9 469.92 577.21 768.38 685.81 1186.13 872.98 1762.73 1218. 12.91 1.01 108.09 1.06 155.52 1.09 196.92 1.12 219.96 1.14 187.81 1.11 5 26.2 446.71 363.36 542.76 625.44 631.46 965.3 768.43 1406.08 991.24 1950.54 1357.57 24.46 1.01 135.11 1.08 174.56 1.11 198.89 1.12 195.84 1.12 136.86 1.08 6 50.67 453.07 498.47 586.81 800. 698.46 1164.19 861.98 1601.92 1109.96 2087.4 1469.25 46.37 1.03 168.89 1.1 195.94 1.12 200.88 1.12 174.37 1.11 99.74 1.06 7 97.03 465.37 667.37 646.94 995.94 782.15 1365.07 968.04 1776.29 1227.58 2187.14 1556.38 87.89 1.05 211.12 1.13 219.93 1.14 202.89 1.12 155.25 1.09 72.68 1.04 8 184.92 489.6 878.48 730.85 1215.87 888.11 1567.96 1088.4 1931.55 1342.76 2259.82 1623.11 166.58 1.1 263.89 1.16 246.87 1.15 204.92 1.13 138.23 1.08 52.96 1.03 9 351.5 539.05 1142.38 851.19 1462.74 1024.22 1772.87 1225.16 2069.78 1454.36 2312.78 1673.53 315.73 1.2 329.87 1.21 277.1 1.17 206.97 1.13 123.07 1.07 38.6 1.02 10 667.23 646.9 1472.25 1029.86 1739.84 1202.01 1979.84 1380.74 2192.85 1561.52 2351.38 1711.26 598.45 1.41 412.34 1.27 311.03 1.2 209.04 1.13 109.58 1.07 28.13 1.02 11 1265.68 914.03 1884.58 1306.82 2050.88 1438.57 2188.87 1557.94 2302.43 1663.55 2379.5 1739.29 1134.3 1.93 515.42 1.35 349.12 1.22 211.13 1.13 97.57 1.06 20.5 1.01 12 2400. 1760. 2400. 1760. 2400. 1760. 2400. 1760. 2400. 1760. 2400. 1760.
- --Cmloegcmluin (talk) 23:39, 11 April 2023 (UTC)
- I'm not sure if this talk page is the best place to continue this discussion about GPS, but here goes anyway. A few thoughts on the above:
- 1. The domain and range of AFS, APS, ALS and GPS have different peculiarities. AFS have only one half of their domain which is musically usable, because the other half results in negative frequencies. APS can be used on its whole domain, since it only outputs positive frequencies, and notably they converge to 0 Hz (−∞ ¢) at one end of the domain. ALS have an issue similar to AFS, because the half of the domain which is associated with negative lengths results in negative frequencies too. GPS behaves a bit like APS, since APS is equivalent to GFS, but on the pitch scale, so it converges to 0 ¢ at one end of the domain, and therefore GPS have either a minimum or a maximum frequency, which is not the case for any of AFS, APS and ALS. In the tables above, the 0 ¢ mark was attributed to step 0 of the scales, so the minimum or maximum pitch would be represented with a different value in cents, but it would still be a finite quantity. For reference, moving the 0 ¢ mark to the value of convergence of each GPS would result in transposing the scales (as opposed to shifting or stretching), if you keep the same frequency for 0 ¢.
- 2. In an APS, the pitch of each degree increases linearly and the size of the steps is constant. In terms of functions, for [math]\displaystyle{ p(x) = ax + b }[/math], the derivative is [math]\displaystyle{ p'(x) = a }[/math] (constant). In a GPS, the pitch of each degree increases (or decreases) exponentially, and the size of the steps also increases (or decreases) exponentially. In terms of functions, for [math]\displaystyle{ p(x) = a b^x + k }[/math], the derivative is [math]\displaystyle{ p'(x) = a \ln(b) b^x }[/math] (proportional to [math]\displaystyle{ p(x) }[/math]).
- 3. This indicates that there are two ways to think of a GPS: defining its exponentially varying steps (intervals) or defining its exponentially varying degrees (pitches). As we saw, the same "geometric factor" applies to both steps and degrees. In your examples, you chose to define the steps, so if we defined a "steps" function, we would have to take the indefinite integral to find the "degrees" function, which would feature an arbitary constant that roughly corresponds to the reference pitch.
- 4. With these function models in mind, it becomes clearer that only one line passes through two given points on a pitch graph, since there is only the parameter [math]\displaystyle{ a }[/math] to work with, but infinitely many exponential graphs pass through these two points, since there are two parameters [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] to work with.
- 5. GPS with a "geometric factor" of 1 are degenerate, because in that case they are constant functions. This is a bit weird though, because constant steps correspond to APS, while constant degrees would be just a single pitch.
- I'm pretty sure I noticed more things, but it's getting late and this is probably enough food for thought for now. I think that framing this in functions with various parameters, experimenting with negative values and with absolute values larger or smaller than 1, and making a difference between the step function and the degree function will help clear out a lot of this. I feel like GPS are a sort of rank-2 family of scales, in the sense that there are two variables to play with, even though rank-2 is probably not the best way to describe how this is behaving. Anyway, that's all for today. --Fredg999 (talk) 05:39, 12 April 2023 (UTC)
- --Cmloegcmluin (talk) 23:39, 11 April 2023 (UTC)
- Thanks for the detailed report! I understand and agree with all above. Yeah, I definitely steered this thread away from its original purpose... Perhaps we should continue this part of the conversation on Discord. I know you started some talk in the #wiki channel there, but perhaps we should start a thread? We could include the relevant materials from here to kick it off. --Cmloegcmluin (talk) 22:21, 12 April 2023 (UTC)
- Good work so far on the edits. I see that all the ADO and IDO pages have been moved to AFDO and IFDO. I had expected that the ADO page would be preserved for Shaahin's original concept, and that you'd start anew with AFDO, but I think you handled things just fine in how you wrote the History section of the page. I just posted some follow-up messages on discussion pages for "Arithmetic MOS" and "Arithmetic interval chain", both of which still need some attention.
- Per Fredg999's suggestion, I have started a discussion for GPS on the Discord server: https://discord.com/channels/332357996569034752/1096541142167846962 --Cmloegcmluin (talk) 21:45, 14 April 2023 (UTC)
- Okay, I have a few updates from Dave, who asked for a link to this discussion and then emailed me about it:
- "The equivalences in this table are strictly by reflection across the main diagonal, not by merely being on the same anti-diagonal." I think that's an excellent generalization, and it explains why I got the color wrong for the GPS cell.
- He also noted that in my tables, I should have had "p → 0", not "p = 0" for geometric sequences.
- He also notes that "quadratic" would be a preferable way to refer to the case of p = 2, rather than RMS, as in "quadratic mean" and "quadratic progression", for better parallelism.
- He also notes that "reciprocal-arithmetic mean" would have been better than "inverse-arithmetic mean". In other words, he thinks RFDO would be clearer than IFDO. For example, if we introduce CompactStar's p=2 scale as a QFDO (quadratic frequency division of the octave), then the "inverse-quadratic mean" would be square-root (p = ½) while "reciprocal-quadratic" would be λx.1/x² (p = -2). But I hesitate even to bring this up, since there's been so much critique of this new naming system already.
- --Cmloegcmluin (talk) 19:13, 19 April 2023 (UTC)
- Dave sent me another email. He points out another issue with the tables I presented above. In the bottom right I have "(of low interest)", but in fact, an ILD is the same thing as an AFD (or as Dave would prefer, because of the "reciprocal" preference over "inverse" issue, an RLD = AFD). --Cmloegcmluin (talk) 17:37, 20 April 2023 (UTC)